Gleichgewichtsbedingungen
Gleichgewichtsbedingungen
3. Momentengleichgewicht
Momentengleichgewicht
Nun gibt es ja nicht nur Kräfte, die auf einen Körper wirken, sondern auch Momente. Und auch Kräfte können eine Momentenwirkung haben. Deswegen muss für einen Körper im Gleichgewicht zusätzlich noch gelten:
Alle Momentenwirkungen, die an einem Körper im Gleichgewicht vorliegen, müssen aufsummiert und bezogen auf einen beliebigen Bezugspunkt \( P \) den Nullvektor ergeben.
Das ist das Momentengleichgewicht.
Der Bezugspunkt \( P \) ist dabei eine rein mathematische Größe, kann also irgendwo liegen. Er muss also insbesondere nicht auf der Struktur liegen, die du betrachtest. Du hast also die Freiheit, den Bezugspunkt clever zu wählen, so dass du beim Aufstellen der Gleichungen möglichst wenig Arbeit hast.
Aber der Reihe nach.
Wie beim Kräftegleichgewicht kannst du das Momentengleichgewicht auch entweder in Vektorschreibweise oder in Komponentenschreibweise aufstellen.
Momentengleichgewicht in Vektorschreibweise:
\( \sum_{j} \vec{M}_j^{P}=\vec{0} \)
Oft werden die Gleichgewichtsbedingungen für die einzelnen Achsrichtungen des Koordinatensystems, also in Komponentenschreibweise, aufgeschrieben. Das sieht dann so aus:
\( \sum_{j} M_{xj}^{P}=0 \)
\( \sum_{j} M_{yj}^{P}=0 \)
\( \sum_{j} M_{zj}^{P}=0 \)
Auch hier schauen wir uns beide Schreibweisen wieder am Beispiel mit dem L-förmigen Balken an.
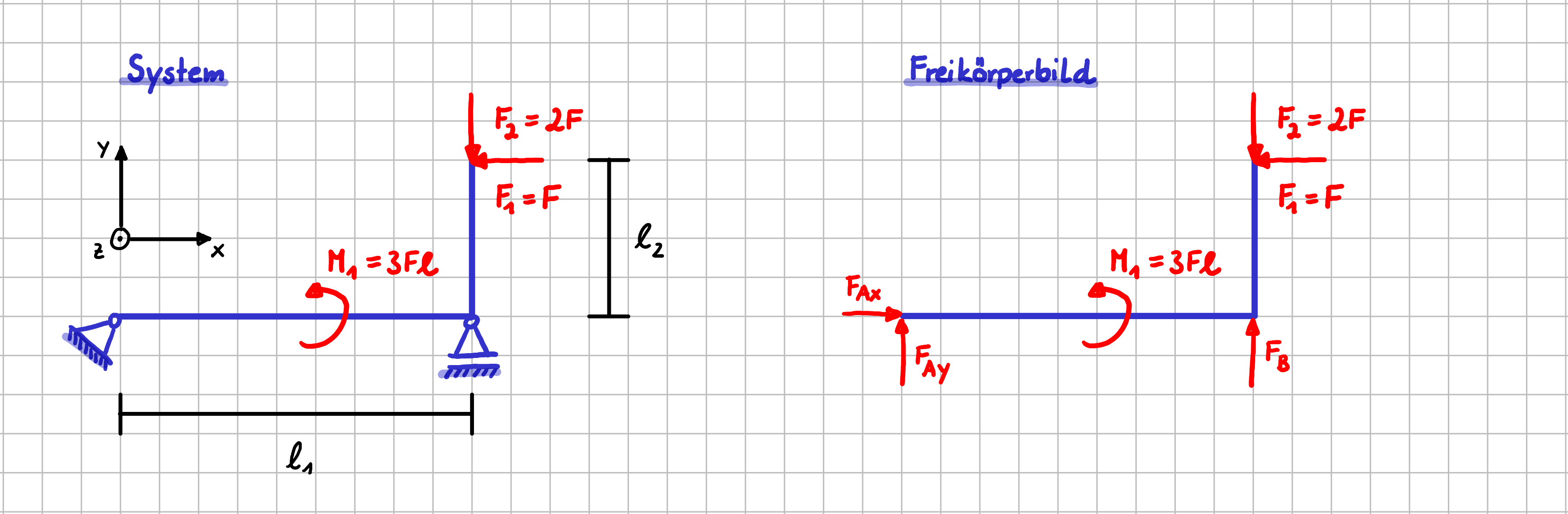
Beispiel für die Betrachtung von Gleichgewichtsbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2201/Gleichgewichtsbedingungen_Beispiel.png
In Vektorschreibweise lautet das Momentegleichgewicht, wenn wir den Punkt \(A\) als Bezugspunkt wählen:
\( \vec{0} = \vec{r}_{AB} \times \vec{F}_B + \vec{r}_{A1} \times \vec{F}_1 + \vec{r}_{A2} \times \vec{F}_2 + \vec{M}_1 \)
Die Ortsvektoren sind hier jeweils Vektoren vom Bezugspunkt \(A\) zu irgendeinem Punkt auf der Wirkungslinie der zugehörigen Kraft. Aber das ist ja ein alter Hut. Das haben wir uns ja im Kapitel Moment schon ausführlich angeschaut:
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix}\ell_1 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\F_{B} \\ 0 \end{pmatrix}+ \begin{pmatrix} \ell_1 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F \\0 \\ 0 \end{pmatrix} + \begin{pmatrix} \ell_1 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\-2F \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\0 \\ -3F\ell \end{pmatrix}\)
ist also genauso korrekt wie
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} \ell_1 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0
\\F_{B} \\ 0 \end{pmatrix}+ \begin{pmatrix} 0 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F
\\0 \\ 0 \end{pmatrix} + \begin{pmatrix} \ell_1 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0
\\-2F \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\0 \\ -3F\ell \end{pmatrix} \)
und liefert
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ \ell_1 \cdot F_B + \ell_2 \cdot F -\ell_1 \cdot 2F-3F\ell\end{pmatrix} \)
Wenn du auf Komponentenebene denken möchtest, würdest du dir als erstes klarmachen, dass es sich bei dem vorliegenden System um ein ebenes Kräftesystem handelt, so dass Momentenwirkungen nur bezüglich der \(z-\)Achse auftreten. Dann kannst du das Momentengleichgewicht bzgl. der \(z-\)Achse im Punkt \(A\) aufstellen, wobei du "Moment = Hebelarm mal Kraft" für die Momentenwirkungen der Einzelkräfte berücksichtigst.
\( \sum M_{z}^{A}=0 =\ell_1 \cdot F_B + \ell_2 \cdot F - \ell_1 \cdot 2F-3F\ell\)
Auch hier kommt erwartungsgemäß bei der vektoriellen und der komponentenweisen Betrachtung dasselbe Ergebnis heraus.
Lerne und übe am besten beiden Varianten. In ebenen Kräftesystemen ist eigentlich immer die komponentenweise Betrachtung schneller. In räumlichen Kräftesystemen ist das Aufstellen und Ausrechnen der Kreuzprodukt oft effizienter.
Wenn du im Moment noch denkst "Bahnhof Gleis 13", dann lies einfach direkt weiter. Im nächsten Abschnitt bekommst du einen Vorschlag für ein Schritt-für-Schritt-Vorgehen bei Gleichgewichtsaufgaben und anschließend findest du noch Beispiele. Wenn du die Beispiele noch einmal durchgearbeitet hast, heißt es "Selber üben, üben, üben" und du wirst schnell sehen, dass es eigentlich ganz einfach ist, Gleichgewichtsaufgaben zu lösen. Aber der Reihe nach ...