Gleichgewichtsbedingungen
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Gleichgewichtsbedingungen |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 14:01 |
1. Einleitung Gleichgewichtsbedingungen
Einleitung Gleichgewichtsbedingungen
Das Aufstellen der Gleichgewichtsbedingungen ist eine immer wiederkehrende Aufgabe, wenn du dich mit statischen Problemen beschäftigst.
Ein starrer Körper ist dann im Gleichgewicht, wenn die Gleichgewichtsbedingungen erfüllt sind.
"Was genau sind denn die Gleichgewichtsbedingungen?", fragst du dich. Mit Gleichgewichtsbedingungen sind das Kräftegleichgewicht und das Momentengleichgewicht gemeint.
Was das genau ist, schauen wir uns in den ersten beiden Abschnitten dieses Kapitels an. Im letzten Abschnitt geht es dann um ein systematisches Vorgehen, wie du Gleichgewichtsaufgaben lösen kannst.
Damit du gut mit den Inhalten dieses Kapitels zurechtkommst, solltest du bereits die Lektionen "Kraft" und "Moment" durchgearbeitet haben und dich gut mit diesen beiden Vektorgrößen auskennen. Denn als Teil der Gleichgewichtsbedingungen werden die Kräfte und Momente, die an einem Körper angreifen, aufsummiert. Es geht also in diesem Sinne mit Kräften und Momenten "auf das nächste Level" und du solltest das vorherige Level erst geschafft haben.
Natürlich ist ein Lernprozess nicht so linear wie das ein oder andere Computerspiel. Von daher plane gerne mit ein, dass du immer wieder zwischen den Lektionen "Gleichgewichtsbedingungen" und "Kraft" und "Moment" hin- und herwechselst. Das ist für einen Lernprozess vollkommen normal und du wirst merken, dass dein Verständnis mit jeder Form der Auseinandersetzung mit den Inhalten wächst und/oder sich vertieft.

Wenn du balancierst erfüllst du ganz intuitiv die Gleichgewichtsbedingungen
Weitere Informationen
2. Kräftegleichgewicht
Kräftegleichgewicht
Bei der Betrachtung von Kräften hatten wir schon festgestellt, dass ein Körper immer dann seinen Bewegungszustand verändert \( - \) also seine Geschwindigkeit zu- oder abnimmt \( - \), wenn Kräfte auf ihn wirken ... es sei denn, er befindet sich in Ruhe und die Resultierende aller am Körper angreifenden Kräfte verschwindet.
Genau das ist auf Kräfte bezogen die Gleichgewichtsbedingung für einen Körper, der in Ruhe ist und auch in Ruhe bleiben soll: Alle Kraftvektoren, die an einem Körper angreifen, müssen aufsummiert den Nullvektor ergeben. Das ist das Kräftegleichgewicht.
Wenn du das Kräftegleichgewicht mathematisch aufschreiben möchtest, hast du zwei unterschiedliche Schreibweisen, die natürlich inhaltlich dasselbe aussagen.Du kannst entweder die Komponentenschreibweise oder die Vektorschreibweise verwenden.
Kräftegleichgewicht in Vektorschreibweise:
\( \sum_{i} \vec{F}_i =\vec{0} \)
Kräftegleichgewicht in Komponentenschreibweise
\( \sum_{i} F_{xi}=0 \)\( \sum_{i} F_{yi}=0 \)
\( \sum_{i} F_{zi}=0 \)
Wie sehen die beiden Schreibweisen ganz konkret für ein System aus?
Schauen wir uns als Beispiel das folgende System und das zugehörige Freikörperbild an: Es besteht aus einer L-förmigen Struktur, die durch die beiden Kräfte \(F_1\) und \(F_2\) belastet wird und mit einem Fest- und einem Loslager gelagert ist.
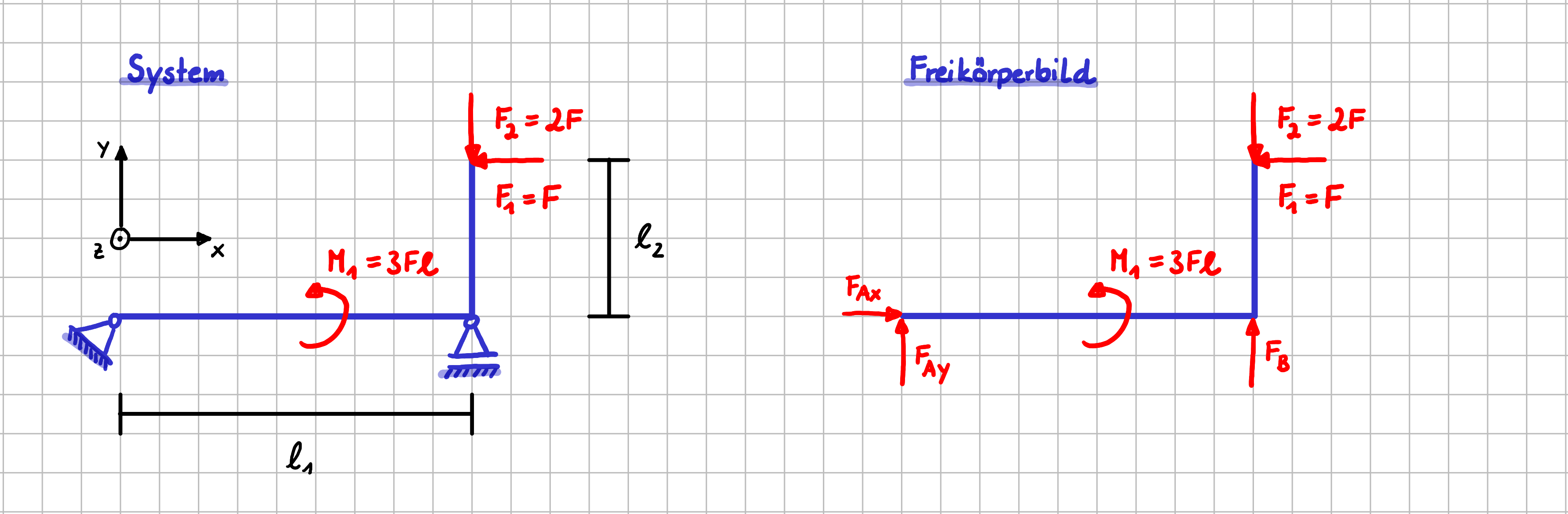
Beispiel für die Betrachtung von Gleichgewichtsbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2198/Gleichgewichtsbedingungen_Beispiel.png
In Vektorschreibweise sieht das Kräftegleichgewicht so aus:
\(\vec{0} = \vec{F}_A + \vec{F}_B + \vec{F}_1 +\vec{F}_2 \)
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} F_{Ax} \\F_{Ay} \\ 0 \end{pmatrix}+ \begin{pmatrix} 0 \\ F_B \\ 0\end{pmatrix}+\begin{pmatrix} -F \\ 0 \\ 0 \end{pmatrix} +\begin{pmatrix} 0 \\ -2F \\ 0 \end{pmatrix}\)
In Komponentenschreibweise würdest du das Kräftegleichgewicht so aufschreiben:
\( \sum F_{x}=0 = F_{Ax} -F \)
\( \sum F_{y}=0 =F_{Ay}+F_B-2F\)
\( \sum F_{z}=0: \text{Keine Kräfte in z-Richtung vorhanden} \)
Statt \( \sum ... =0 \) zu schreiben, gibt es auch noch eine andere Schreibweise, bei der mit Pfeilen die Richtung angegeben wird, in der man die Kraftkomponenten aufsummiert. Das sieht für unser Beispiel dann so aus:
\( \rightarrow \quad: \qquad 0 = F_{Ax} -F \)
\( \uparrow\quad: \qquad 0 =F_{Ay}+F_B-2F\)
Manche Professoren kombinieren auch beide Schreibweisen, was ich persönlich doppeltgemoppelt finde. Das sieht dann so aus:
\( \rightarrow \sum F_{x}=0 = F_{Ax} -F \)
\( \uparrow \sum F_{y}=0 =F_{Ay}+F_B-2F\)
3. Momentengleichgewicht
Momentengleichgewicht
Nun gibt es ja nicht nur Kräfte, die auf einen Körper wirken, sondern auch Momente. Und auch Kräfte können eine Momentenwirkung haben. Deswegen muss für einen Körper im Gleichgewicht zusätzlich noch gelten:
Alle Momentenwirkungen, die an einem Körper im Gleichgewicht vorliegen, müssen aufsummiert und bezogen auf einen beliebigen Bezugspunkt \( P \) den Nullvektor ergeben.
Das ist das Momentengleichgewicht.
Der Bezugspunkt \( P \) ist dabei eine rein mathematische Größe, kann also irgendwo liegen. Er muss also insbesondere nicht auf der Struktur liegen, die du betrachtest. Du hast also die Freiheit, den Bezugspunkt clever zu wählen, so dass du beim Aufstellen der Gleichungen möglichst wenig Arbeit hast.
Aber der Reihe nach.
Wie beim Kräftegleichgewicht kannst du das Momentengleichgewicht auch entweder in Vektorschreibweise oder in Komponentenschreibweise aufstellen.
Momentengleichgewicht in Vektorschreibweise:
\( \sum_{j} \vec{M}_j^{P}=\vec{0} \)
Oft werden die Gleichgewichtsbedingungen für die einzelnen Achsrichtungen des Koordinatensystems, also in Komponentenschreibweise, aufgeschrieben. Das sieht dann so aus:
\( \sum_{j} M_{xj}^{P}=0 \)
\( \sum_{j} M_{yj}^{P}=0 \)
\( \sum_{j} M_{zj}^{P}=0 \)
Auch hier schauen wir uns beide Schreibweisen wieder am Beispiel mit dem L-förmigen Balken an.
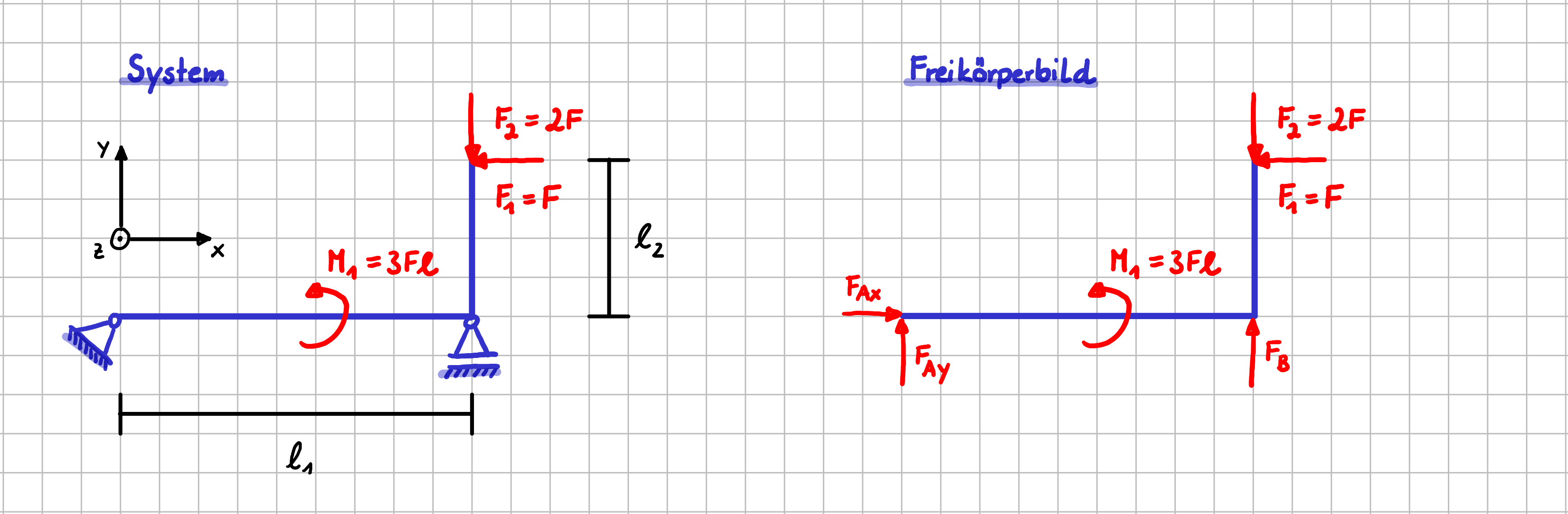
Beispiel für die Betrachtung von Gleichgewichtsbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2201/Gleichgewichtsbedingungen_Beispiel.png
In Vektorschreibweise lautet das Momentegleichgewicht, wenn wir den Punkt \(A\) als Bezugspunkt wählen:
\( \vec{0} = \vec{r}_{AB} \times \vec{F}_B + \vec{r}_{A1} \times \vec{F}_1 + \vec{r}_{A2} \times \vec{F}_2 + \vec{M}_1 \)
Die Ortsvektoren sind hier jeweils Vektoren vom Bezugspunkt \(A\) zu irgendeinem Punkt auf der Wirkungslinie der zugehörigen Kraft. Aber das ist ja ein alter Hut. Das haben wir uns ja im Kapitel Moment schon ausführlich angeschaut:
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix}\ell_1 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\F_{B} \\ 0 \end{pmatrix}+ \begin{pmatrix} \ell_1 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F \\0 \\ 0 \end{pmatrix} + \begin{pmatrix} \ell_1 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0 \\-2F \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\0 \\ -3F\ell \end{pmatrix}\)
ist also genauso korrekt wie
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} \ell_1 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0
\\F_{B} \\ 0 \end{pmatrix}+ \begin{pmatrix} 0 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F
\\0 \\ 0 \end{pmatrix} + \begin{pmatrix} \ell_1 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} 0
\\-2F \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\0 \\ -3F\ell \end{pmatrix} \)
und liefert
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ \ell_1 \cdot F_B + \ell_2 \cdot F -\ell_1 \cdot 2F-3F\ell\end{pmatrix} \)
Wenn du auf Komponentenebene denken möchtest, würdest du dir als erstes klarmachen, dass es sich bei dem vorliegenden System um ein ebenes Kräftesystem handelt, so dass Momentenwirkungen nur bezüglich der \(z-\)Achse auftreten. Dann kannst du das Momentengleichgewicht bzgl. der \(z-\)Achse im Punkt \(A\) aufstellen, wobei du "Moment = Hebelarm mal Kraft" für die Momentenwirkungen der Einzelkräfte berücksichtigst.
\( \sum M_{z}^{A}=0 =\ell_1 \cdot F_B + \ell_2 \cdot F - \ell_1 \cdot 2F-3F\ell\)
Auch hier kommt erwartungsgemäß bei der vektoriellen und der komponentenweisen Betrachtung dasselbe Ergebnis heraus.
Lerne und übe am besten beiden Varianten. In ebenen Kräftesystemen ist eigentlich immer die komponentenweise Betrachtung schneller. In räumlichen Kräftesystemen ist das Aufstellen und Ausrechnen der Kreuzprodukt oft effizienter.
Wenn du im Moment noch denkst "Bahnhof Gleis 13", dann lies einfach direkt weiter. Im nächsten Abschnitt bekommst du einen Vorschlag für ein Schritt-für-Schritt-Vorgehen bei Gleichgewichtsaufgaben und anschließend findest du noch Beispiele. Wenn du die Beispiele noch einmal durchgearbeitet hast, heißt es "Selber üben, üben, üben" und du wirst schnell sehen, dass es eigentlich ganz einfach ist, Gleichgewichtsaufgaben zu lösen. Aber der Reihe nach ...
4. Vorgehen bei Gleichgewichtsaufgaben
Vorgehen bei Gleichgewichtsaufgaben
Mir hat es immer geholfen, mich erstmal an einem Ablaufplan langzuhangeln, gerade wenn ich mit meiner Beschäftigung mit einem Themengebiet noch ganz am Anfang stand. Vielleicht geht es dir auch so? Und ein systematisches Vorgehen ist ja eigentlich immer hilfreich, gerade bei komplexeren Aufgaben, oder?
Deshalb findest du in der folgenden Abbildung einen Vorschlag für ein systematisches Vorgehen. Wie du dann ganz praktisch damit arbeiten kannst, schauen wir uns dann gleich danach an mehreren Beispielen an.

7-Schritte-Ablaufplan für das systematische Lösen von Gleichgewichtsaufgaben
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2199/Sieben_Schritte_Ablaufplan_Gleichgewichtsaufgaben.png
Wir wollen uns eine Leiter anschauen, die an eine Hauswand gelehnt ist und am Fußpunkt an einer Erhebung im Boden abgestützt ist. Das ist übrigens ein ganz reales Problem, da es immer genau so aussieht, wenn wir die Leiter rausholen, um unsere Dachrinnen sauber zu machen. Auf der Mitte der Leiter steht eine Person mit Gewichtskraft \( G \). Die Hauswand ist relativ glatt, weshalb sie als reibungsfrei modelliert wird. Der Anstellwinkel der Leiter ist \(\alpha\) und die Länge ist \( \ell \).
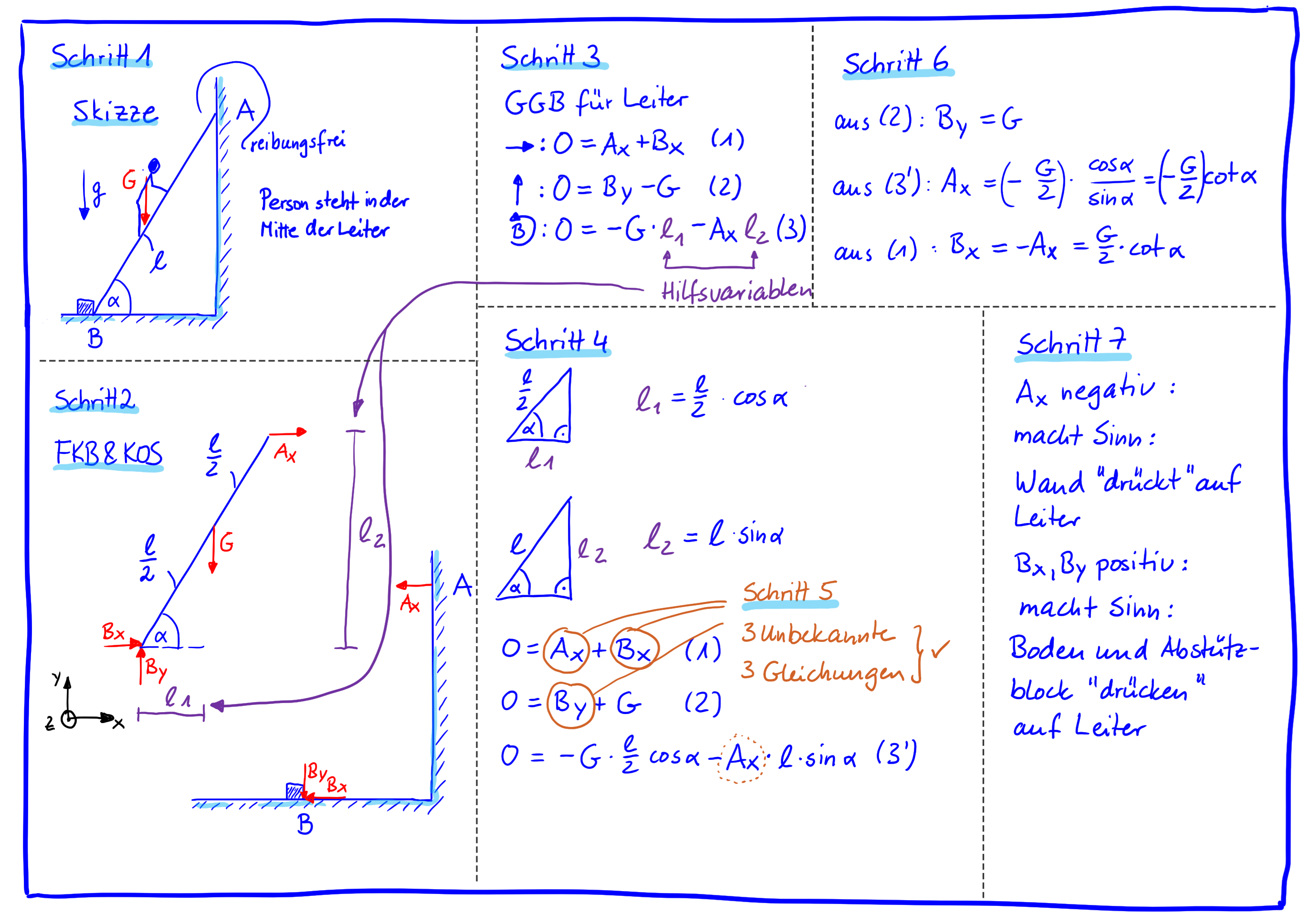
Person auf Anlehnleiter als Beispiel für eine Gleichgewichtsaufgabe- gelöst nach dem 7-Schritte-Ablaufplan (Komponentenschreibweise)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2199/Person_auf_Anlehnleiter_Komponentenschreibweise.png
Zunächst erstellst du eine Skizze des Systems und trägst alle Informationen ein, die du hast. Das ist Schritt 1. Dann erstellst du in Schritt 2 ein Freikörperbild für das System. Du schneidest also in diesem Fall die Leiter von der Umgebung ein und trägst neben der eingeprägten Kraft, also der Gewichtskraft, die Reaktionskräfte in den Lagerpunkten \( A \) und \( B \) ein. Da der Kontakt bei \( A \) als reibungsfrei angenommen wird, bedeutet dies, dass hier nur eine Normalkraft, also eine Kraft senkrecht zur Wand übertragen werden kann. Weil in der Aufgabe noch kein Koordinatensystem gegeben war, wählst du selber eins und bezeichnest die Lagerkräfte anschließend sinnvoll. Da alle Kräfte in horizontaler und vertikaler Richtung wirken, ist es naheliegend, auch die Achsen des Koordinatensystems in diese Richtung auszurichten. Es ist üblich, die Kräfte nach dem Punkt zu benennen, in dem sie angreifen, und als Index noch die Koordinatenrichtung, in die sie zeigen, zu verwenden. Da es am Punkt \( B \) eine Kraftkomponente in \( x \)-Richtung und eine in \( y \)-Richtung gibt, heißen die Kräfte hier also \( B_x \) und \( B_y \).
Jetzt passiert das, worum es in diesem Abschnitt geht: Du stellst die Gleichgewichtsbedingungen (GGB) für die Leiter auf. In Schritt 3 verwendest du hierbei erstmal Hilfsvariablen (Spoiler: in diesem Beispiel sind es die Hebelarme), damit du schnell und zügig die GGB komplett aufschreiben kannst, ohne dir über irgendwelche geometrischen Zusammenhänge Gedanken machen zu müssen. Da es sich hier um ein ebenes System handelt, wobei die Wirkungslinien der Kräfte in der \( xy \)-Ebene liegen, wird das Kräftegleichgewicht für die \( x \)- und die \( y \)-Richtung aufgestellt; das Momentengleichgewicht dementsprechend um die \( z \)-Achse. Die Kräfte \( A_x \) und \( B_z \) zeigen, so wie sie im Freikörperbild eingezeichnet sind, in positive Koordinatenrichtung. Deswegen gehen sie mit einem Pluszeichen ins Kräftegleichgewicht ein. Das Gleiche gilt für \( B_y \)und die \( y \)-Richtung. Für das Momentengleichgewicht kannst du einen beliebigen Bezugspunkt wählen. Es gibt kein "falsch" oder "richtig". Punkt \( B \) zu wählen ist clever, da durch diesen Punkt die Wirkungslinien zweier unbekannter Kräfte durchgehen. Sie tauchen so nicht im Momentengleichgewicht auf, wodurch diese Gleichung einfach wird. Für das Momentengleichgewicht werden noch die Hebelarme von \( G \) und \( A_x \) benötigt. Da diese nicht direkt in der Systemzeichnung gegeben sind, ist das der ideale Zeitpunkt um für sie die Hilfsvariablen \( \ell_1 \) und \( \ell_2 \) einzuführen. Dann ist auch das Momentengleichgewicht schnell und vollständig aufgeschrieben, wenn du die Rechte-Hand-Regel berücksichtigst: Rechte-Faust in Punkt \( B \) legen, Daumen in Richtung der positiven \( z \)-Achse strecken und prürfen, ob die Kräfte mit ihrem Hebelarm in Richtung der restlichen Finger drehen würde oder nicht. Sowohl \( G \) als auch \( A_x \) drehen entgegen der restlichen Finger, weshalb beide Momente mit einem negativen Vorzeichen in das Momentengleichgewicht eingehen. In Schritt 4 hast du keine mechanische, sondern eine rein geometrische Aufgabe zu lösen. Du müsst die Hilfsvariablen \( \ell_1 \) und \( \ell_2 \), also die Hebelarme der beiden Kräfte, durch gegebene Größen ausdrücken. Dazu kannst du dir die jeweiligen rechtwinkligen Dreiecke nochmal hinzeichnen und mit Hilfe der Sinus- und der Cosinusfunktion die gesuchten Zusammenhänge bestimmen. Dann ist es schon fast geschafft. An dieser Stelle (Schritt 5) oder auch schon früher lohnt es sich, einmal zu schauen, wie viele Unbekannte Größen und wie viele Gleichungen du hast. Es sind drei Unbekannte Lagerkräfte und drei Gleichgewichtsbedingungen. Das macht doch Laune, da klar ist, dass die Werte aller Lagerkräfte ausgerechnet werden können. Und genau das machst du in Schritt 6 durch Umformen und einsetzen der drei Gleichungen. Abschließend bei jeder Rechnung solltest du noch einen Plausibilitätscheck durchführen. Das ist Schritt 7. In diesem Beispiel bietet es sich an, die Vorzeichen der Ergebnisse zu überprüfen. Es ist aufgrund des realen Problems bereits nach Erstellen des Freikörperbilds klar, dass bei der gewählten Richtung für \( A_x \) ein negatives Vorzeichen herauskommen muss. Die Leiter stützt sich schließlich an der Wand ab. Und siehe da: das berechnete Ergebnis ist in der Tat negativ. Check für diese Kraft erfolgreich absolviert. Genauso kannst du die Vorzeichen der Kräfte im Punkt \( B \) prüfen.
Bei der Lösungsvariante eben habe ich die Komponenteschreibweise in Schritt 3 verwendet. Du kannst natürlich genauso gut die Vektorschreibweise verwenden. Dazu musst du als erstes alle auftretenden Kräfte und Momente als Vektoren aufschreiben. Dann kannst du wieder die Gleichgewichtsbedingungen hinschreiben.
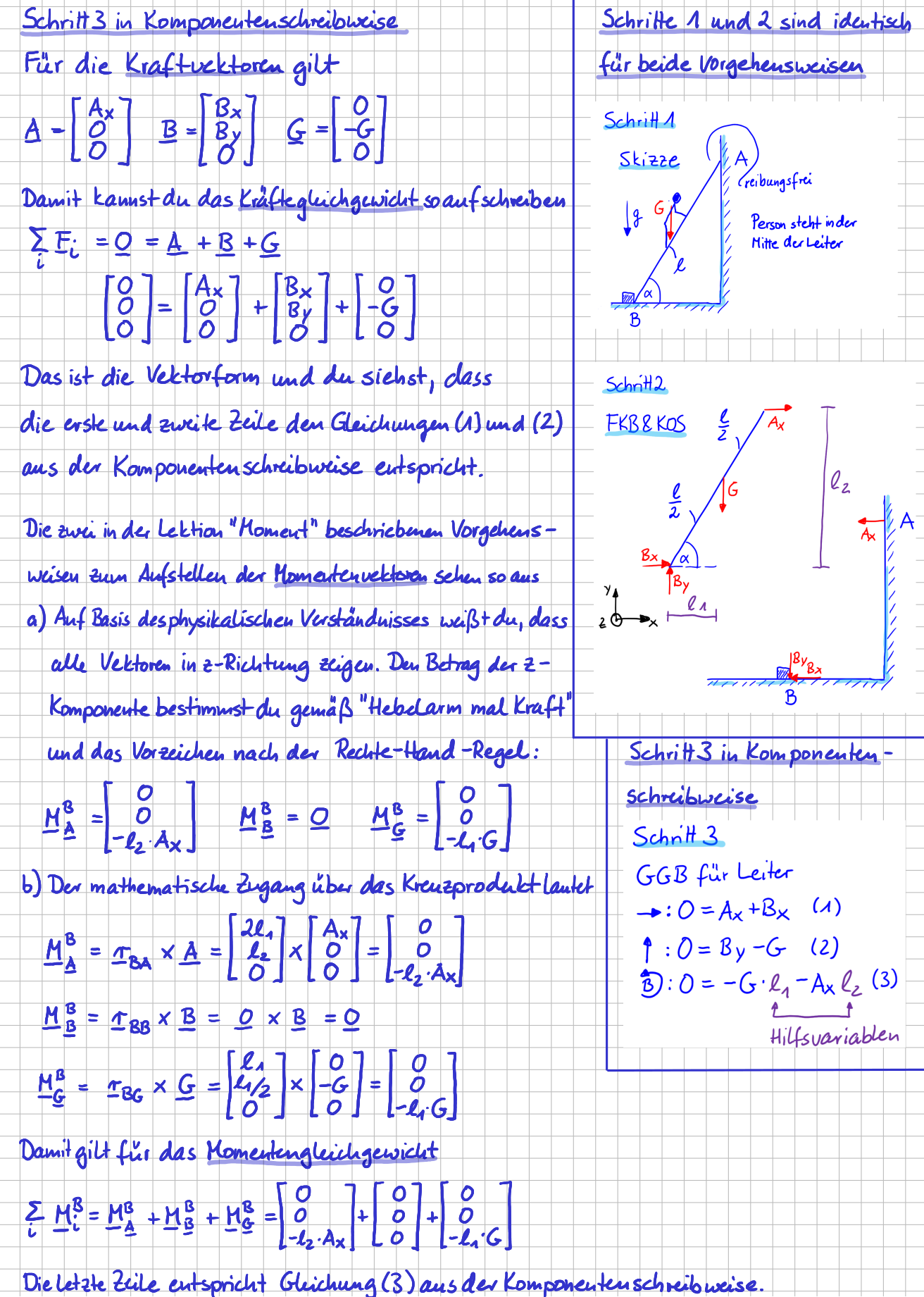
Person auf Anlehnleiter als Beispiel für eine Gleichgewichtsaufgabe- Schritt 3 in der Vektorschreibweise
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2199/Person_auf_Anlehnleiter_Vektorschreibweise.png
Die Vektorschreibweise erscheint erst einmal deutlich aufwendiger. Bedenke, dass es sich bei dem betrachteten Beispiel "nur" um ein ebenes System handelt. Da ist die Komponentenschreibweise in der Regel übersichtlicher und du kommst schneller zum Ziel. Für räumliche Systeme sieht die Welt aber meist anders aus. Hier hat die Vektorschreibweise viele Vorteile. Und wie immer gilt: je mehr Werkzeuge du beherrschst, desto flexibler kannst du dich je nach Anwendungsfall für das passendere Werkzeug entscheiden.
Bei Schritt 2 "Freikörperbild erstellen" hast du dir vielleicht schon mal die Frage gestellt, ob es eine Rolle spielt, wie, also in welche Richtungen, du die Reaktionsgrößen beim Freischneiden einzeichnest.
Ich habe mal ein einfaches System genommen und für zwei unterschiedliche durchgespielt: links habe ich am Körper alle Reaktionsgrößen in positive Achsrichtung angenommen; rechts habe ich ein Mischmasch an Richtungen gewählt, weshalb ich diese Variante “freestyle” genannt habe. Schau selbst, wie sich unterschiedliche Wahl der Richtungen bemerkbar macht.

Auswirkungen der Wahl der Richtungen der Reaktionsgrößen beim Freischneiden.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2199/Auswirkungen_der_Richtungen_der_Reaktionsgroessen_beim_Freischneiden.png
Es gibt also kein 'richtig' oder 'falsch' beim Einzeichnen der Richtungen von Reaktionsgrößen im Freikörperbild (Natürlich musst du Actio = Reactio beachten !!!): eingezeichnete Richtungen und erhaltene Vorzeichen musst du immer zusammenbetrachten.
Zu Schritt 3 und Schritt 4 "Gleichgewichtsbedingungen mit Hilfsvariablen aufstellen" und "Hilfsvariablen bestimmen und einsetzen" möchte ich dir noch weitere Beispiele zeigen. Du fragst dich vielleicht: Wo und wann ist es denn sinnvoll, Hilfsvariablen einzuführen? Das es sinnvoll ist, Hilfsvariablen für nicht sofort ersichtliche Hebelarme einzuführen, hast du im Leiterbeispiel schon gesehen. Genauso kannst du Kraftkomponenten erstmal in Schritt 3 als Hilfsvariablen einführen und dann in Schritt 4 konkret berechnen, wie im folgenden Beispiel:
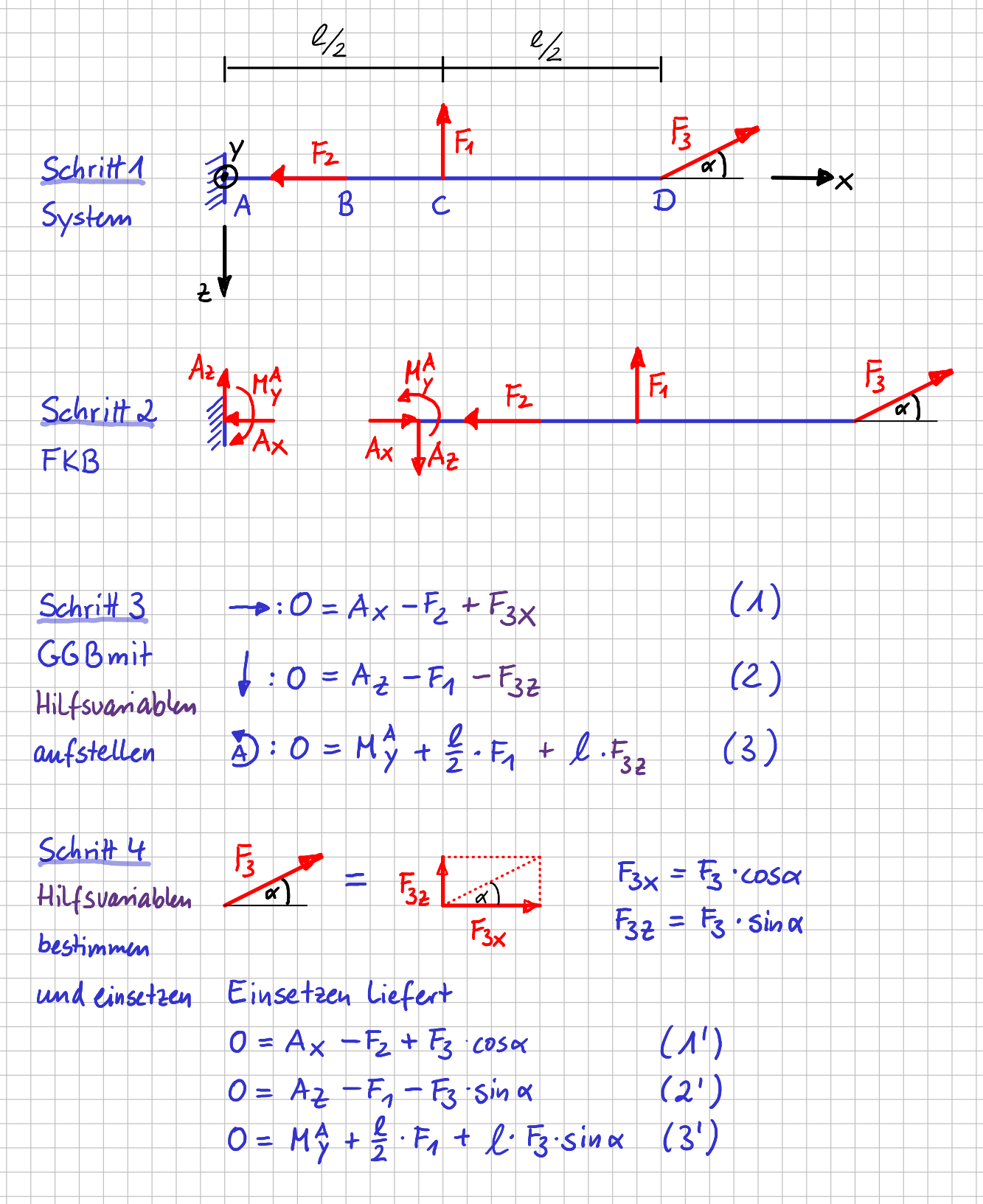
Beispiel mit Kraftkomponenten als Hilfsvariablen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2199/Beispiel_mit_Kraftkomponenten_als_Hilfsvariablen.png
Oder wenn du eine Streckenlast hast, ist es hilfreich, für die resultierende Einzelkraft \( F_q \) und ihren Hebelarm in Schritt 3 erstmal Hilfsvariablen einzuführen, um die Gleichgewichtsbedingungen 'schnell' vollständig hinschreiben zu können. In Schritt 4 kannst du dich dann anschließend ganz entspannt um die Bestimmung der genauen Werte des Betrags der Kraft und des Hebelarms kümmern, so wie in diesem Beispiel:
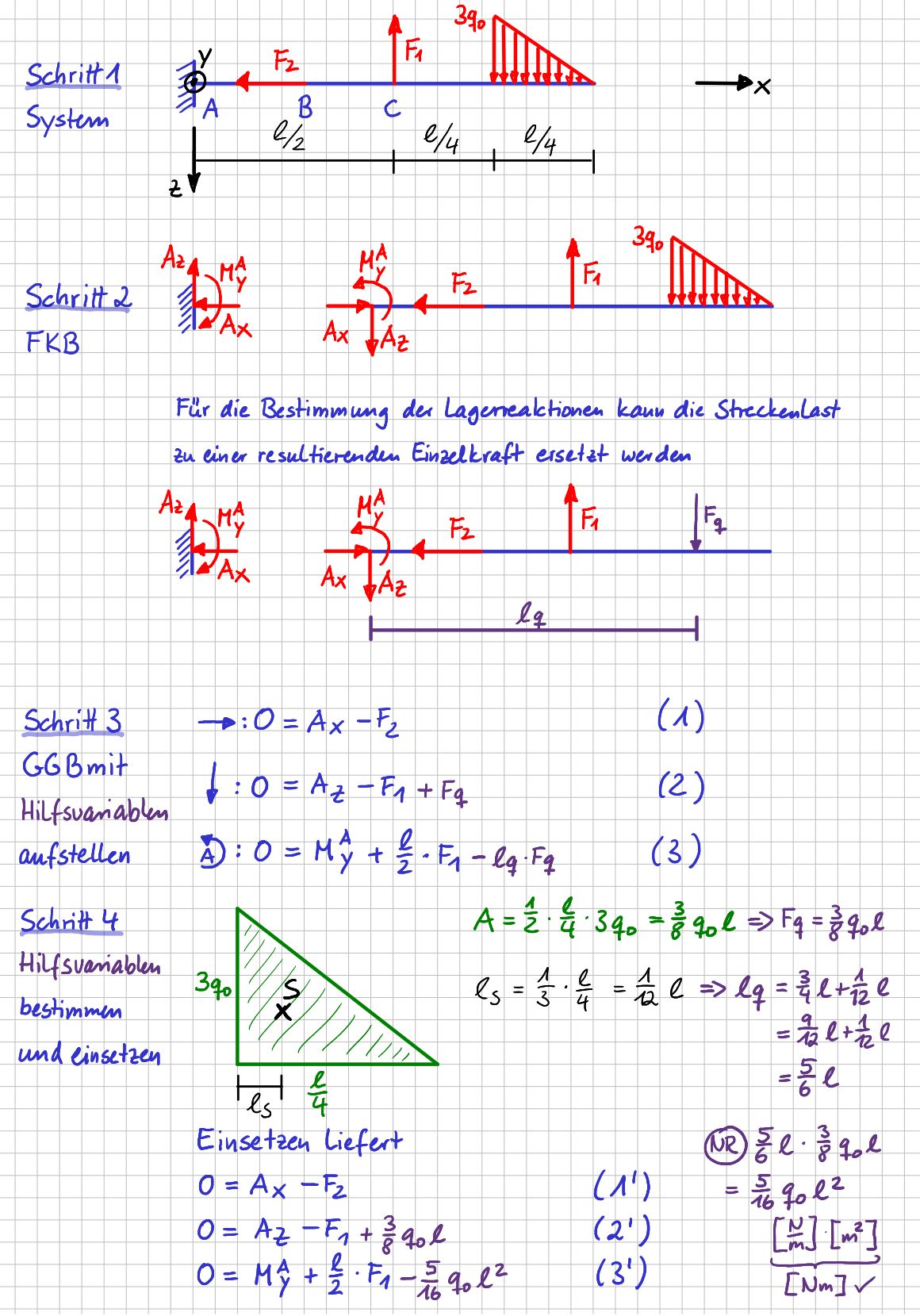
Beispiel mit resultierender Kraft einer Streckenlast und ihrem Hebelarm als Hilfsvariable
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2199/Beispiel_Streckenlast_mit_Hilfsvariable.png
Am Anfang sieht es für dich vielleicht so aus, als wären solche Gleichgewichtsaufgaben, in denen es ja meist darum geht, unbekannte Lagerreaktionen zu bestimmen, fürchterlich aufwendig. Du wirst aber sehen, dass du die einzelnen Schritte irgendwann wie im Schlaf machst, wenn du ganz viele Aufgaben gerechnet hast.
Zusammenfassung - Das Wichtigste in Kürze

7-Schritte-Ablaufplan für das systematische Lösen von Gleichgewichtsaufgaben mit Beispiel
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2199/Sieben_Schritte_Ablaufplan_Gleichgewichtsaufgaben.png?time=1735559000891
