Gleichgewichtsbedingungen
Gleichgewichtsbedingungen
2. Kräftegleichgewicht
Kräftegleichgewicht
Bei der Betrachtung von Kräften hatten wir schon festgestellt, dass ein Körper immer dann seinen Bewegungszustand verändert \( - \) also seine Geschwindigkeit zu- oder abnimmt \( - \), wenn Kräfte auf ihn wirken ... es sei denn, er befindet sich in Ruhe und die Resultierende aller am Körper angreifenden Kräfte verschwindet.
Genau das ist auf Kräfte bezogen die Gleichgewichtsbedingung für einen Körper, der in Ruhe ist und auch in Ruhe bleiben soll: Alle Kraftvektoren, die an einem Körper angreifen, müssen aufsummiert den Nullvektor ergeben. Das ist das Kräftegleichgewicht.
Wenn du das Kräftegleichgewicht mathematisch aufschreiben möchtest, hast du zwei unterschiedliche Schreibweisen, die natürlich inhaltlich dasselbe aussagen.Du kannst entweder die Komponentenschreibweise oder die Vektorschreibweise verwenden.
Kräftegleichgewicht in Vektorschreibweise:
\( \sum_{i} \vec{F}_i =\vec{0} \)
Kräftegleichgewicht in Komponentenschreibweise
\( \sum_{i} F_{xi}=0 \)\( \sum_{i} F_{yi}=0 \)
\( \sum_{i} F_{zi}=0 \)
Wie sehen die beiden Schreibweisen ganz konkret für ein System aus?
Schauen wir uns als Beispiel das folgende System und das zugehörige Freikörperbild an: Es besteht aus einer L-förmigen Struktur, die durch die beiden Kräfte \(F_1\) und \(F_2\) belastet wird und mit einem Fest- und einem Loslager gelagert ist.
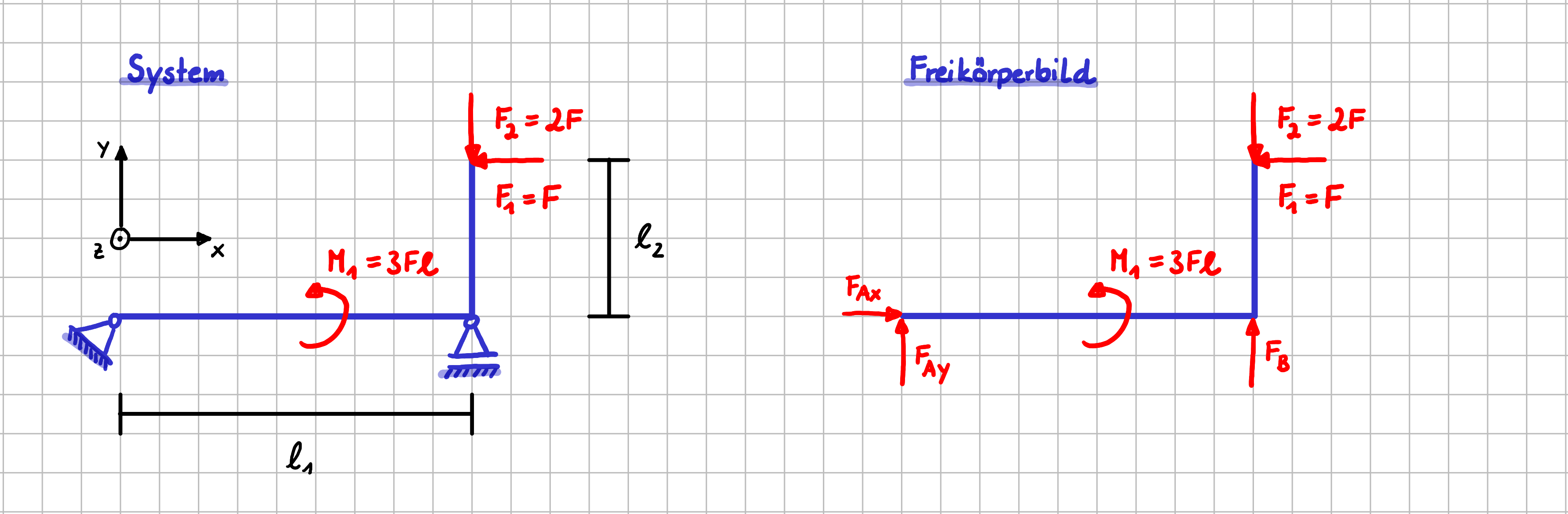
Beispiel für die Betrachtung von Gleichgewichtsbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13822/mod_book/chapter/2198/Gleichgewichtsbedingungen_Beispiel.png
In Vektorschreibweise sieht das Kräftegleichgewicht so aus:
\(\vec{0} = \vec{F}_A + \vec{F}_B + \vec{F}_1 +\vec{F}_2 \)
\( \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} F_{Ax} \\F_{Ay} \\ 0 \end{pmatrix}+ \begin{pmatrix} 0 \\ F_B \\ 0\end{pmatrix}+\begin{pmatrix} -F \\ 0 \\ 0 \end{pmatrix} +\begin{pmatrix} 0 \\ -2F \\ 0 \end{pmatrix}\)
In Komponentenschreibweise würdest du das Kräftegleichgewicht so aufschreiben:
\( \sum F_{x}=0 = F_{Ax} -F \)
\( \sum F_{y}=0 =F_{Ay}+F_B-2F\)
\( \sum F_{z}=0: \text{Keine Kräfte in z-Richtung vorhanden} \)
Statt \( \sum ... =0 \) zu schreiben, gibt es auch noch eine andere Schreibweise, bei der mit Pfeilen die Richtung angegeben wird, in der man die Kraftkomponenten aufsummiert. Das sieht für unser Beispiel dann so aus:
\( \rightarrow \quad: \qquad 0 = F_{Ax} -F \)
\( \uparrow\quad: \qquad 0 =F_{Ay}+F_B-2F\)
Manche Professoren kombinieren auch beide Schreibweisen, was ich persönlich doppeltgemoppelt finde. Das sieht dann so aus:
\( \rightarrow \sum F_{x}=0 = F_{Ax} -F \)
\( \uparrow \sum F_{y}=0 =F_{Ay}+F_B-2F\)