Lager: Lager in ebenen Systemen

3. Lager in ebenen Systemen

Lager in ebenen Systemen

Zunächst wollen wir uns Lager anschauen, die in Systemen zum Einsatz kommen, die ebene Systeme sind oder als ebene Systeme modelliert werden können.
Erinnerst du dich noch daran, was ein ebenes System kennzeichnet? Die Wirkungslinien der auftretenden Kräfte und die Ortsvektoren liegen alle in einer Ebene. Momente können daher nur um Achsen senkrecht zu dieser Ebene auftreten.

Für die potentiellen Bewegungsmöglichkeiten bedeutet dies:
im ebenen Fall hat ein Körper drei Freiheitsgrade:
zwei Verschiebungen (= zwei Translationsfreiheitsgrade) und
eine Drehung (= einen Rotationsfreiheitsgrad).
Es sind also genau diese drei Freiheitsgrade, die von Lagern eingeschränkt werden können.

Wird eine Verschiebungsmöglichkeit durch ein Lager behindert, tritt eine Reaktionskraft im Lager auf. Wird eine Drehung durch ein Lager behindert, tritt ein Reaktionsmoment im Lager auf.

Reaktionskräfte und -momente bezeichnet man als Reaktionsgrößen.

Es können im ebenen Fall also maximal drei Reaktionsgrößen - zwei Reaktionskräfte und ein Reaktionsmoment - in einem Lager auftreten.

Um diese Reaktionsgrößen in einem System sichtbar zu machen, müssen die Lager freigeschnitten werden.

Hinweis

Ein ganz (!) wichtiger Hinweis an dieser Stelle: verschiedene Lagertypen haben ihre spezifische Funktion unabhängig von der Wahl eines Koordinatensystems, also rein aufgrund ihrer Bauart, rein aufgrund der Physik. Deswegen ist es wichtig, dass du dich auch ohne ein Koordinatensystem mit ihnen vertraut machst.

Ein Lager, das den einen Verschiebungsfreiheitsgrad eines Körpers behindert, aber den zweiten Verschiebungsfreiheitsgrad und den Rotationsfreiheitsgrad frei lässt, ist das im folgenden Bild dargestellte Lager. Es wird als Loslager bezeichnet.

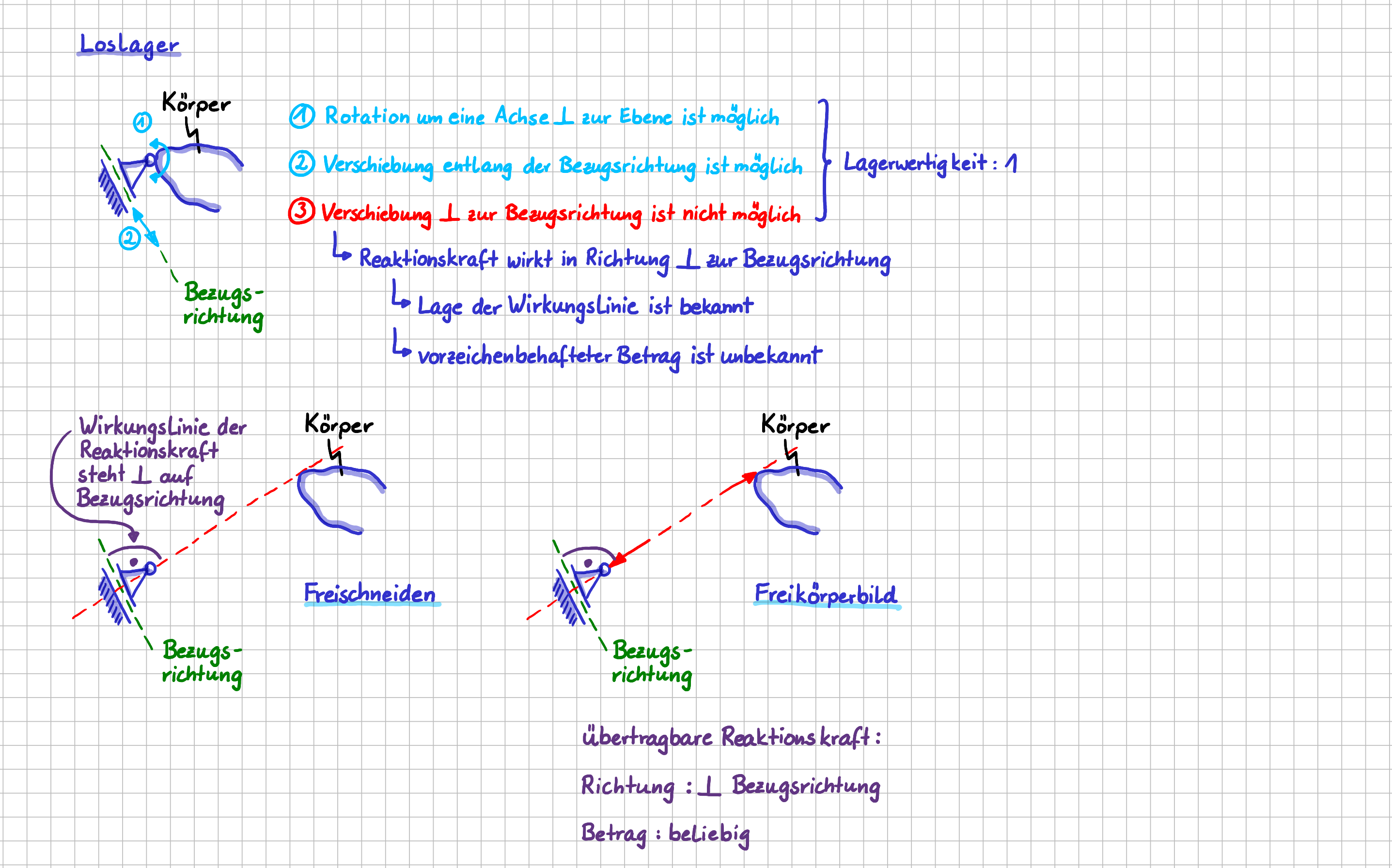
Loslager im ebenen System

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13820/mod_book/chapter/2189/Loslager_im_ebenen_System.png

Kennzeichnend für das Loslager ist die mögliche Richtung der Verschiebung, die als Bezugsrichtung bezeichnet wird. Die physikalische Funktion eines Loslagers kannst du mit dieser Bezugsrichtung ganz einfach angeben: Ein Loslager kann senkrecht zur Bezugsrichtung eine vom Betrag her beliebige Kraft übertragen.
Beim Loslager ist die Richtung der Reaktionskraft im Lager also aufgrund des Lagertyps von vornherein klar. Du musst also 'nur' den (vorzeichenbehafteten) Betrag dieser Kraft durch Auswerten der Gleichgewichtsbedingungen bestimmen.

Merkst du, dass du gar kein Koordinatensystem brauchst, um die Funktion dieses Lagers zu beschreiben?
Genau das ist mit dem Hinweis weiter oben gemeint.

Ein Loslager ist ein 1-wertiges Lager, da es einen Freiheitsgrad behindert = eine Reaktionsgröße übertragen kann.

Als Festlager bezeichnet man ein Lager, dass beide Verschiebungsfreiheitsgrade eines Körpers im ebenen System behindert. Eine Rotation ist nach wie vor möglich.

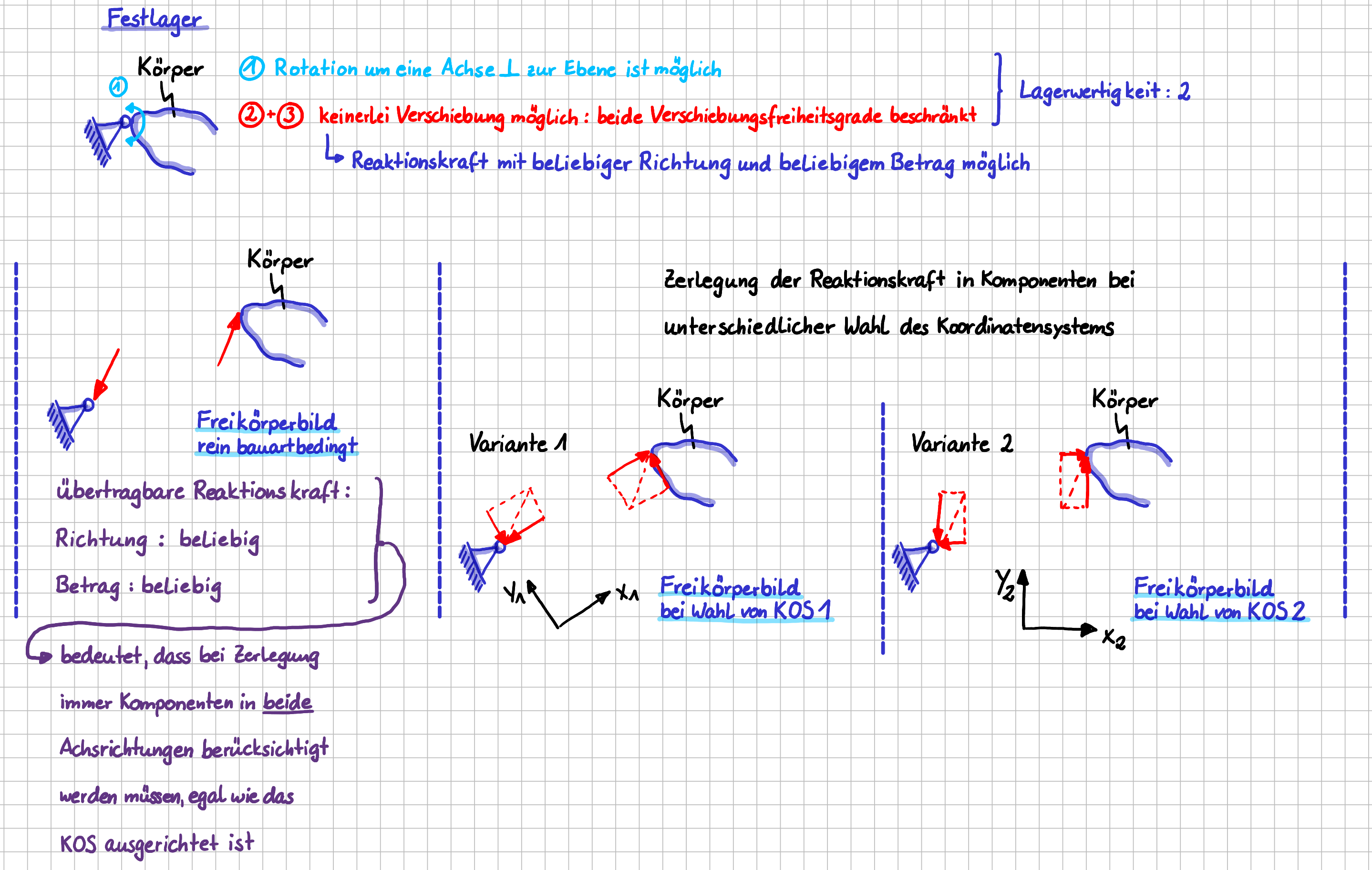
Festlager im ebenen System

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13820/mod_book/chapter/2189/Festlager_im_ebenen_System.png

Wie sieht es hier mit dem physikalischen Verständnis aus? Oder anders gefragt: Wie kannst du die Funktion eines Festlagers beschreiben, ohne dafür ein Koordinatensystem zu verwenden?

Ein Festlager ist ein Lager, dass eine Reaktionskraft in einer beliebigen Richtung und mit einem beliebigen Betrag übertragen kann. So ist es im obigen Bild links dargestellt. Anders als beim Loslager sind also (vorzeichenbehafteter) Betrag UND Richtung unbekannt. Betrag und Richtung verändern sich, je nachdem, wie die Belastungen z.B. durch äußere Kräfte und Momente im System sind.
Genauso gut kannst du sagen, dass ein Festlager beliebige Kraftkomponenten in zwei zueinander senkrechten Richtungen übertragen kann.

Damit ist die physikalische Funktion eines Festlagers klar.

Welche Konsequenzen bzw., passender formuliert, welche Möglichkeiten ergeben sich beim Erstellen des Freikörperbilds beim Freischneiden eines Festlagers?

Wenn ein Festlager dadurch gekennzeichnet ist, dass es beliebige Kraftkomponenten in zwei zueinander senkrechten Richtungen übertragen kann, dann macht es doch Sinn, diese Kraftkomponenten auf die beiden Achsrichtungen zu legen, oder?

Dies siehst du im oberen Bild in der Mitte und rechts exemplarisch für zwei verschiedene Koordinatensysteme.

Weiter unten schauen wir uns an einem Fachwerksystem an, in wie weit du ein 'cleveres' oder ' nicht so cleveres' Koordinatensystem wählen kannst.

Als letztes Lager wollen wir uns noch detailliert die feste Einspannung anschauen. Bei der festen Einspannung ist im Vergleich zum Festlager zusätzlich noch die Drehung, also der Rotationsfreiheitsgrad, behindert.

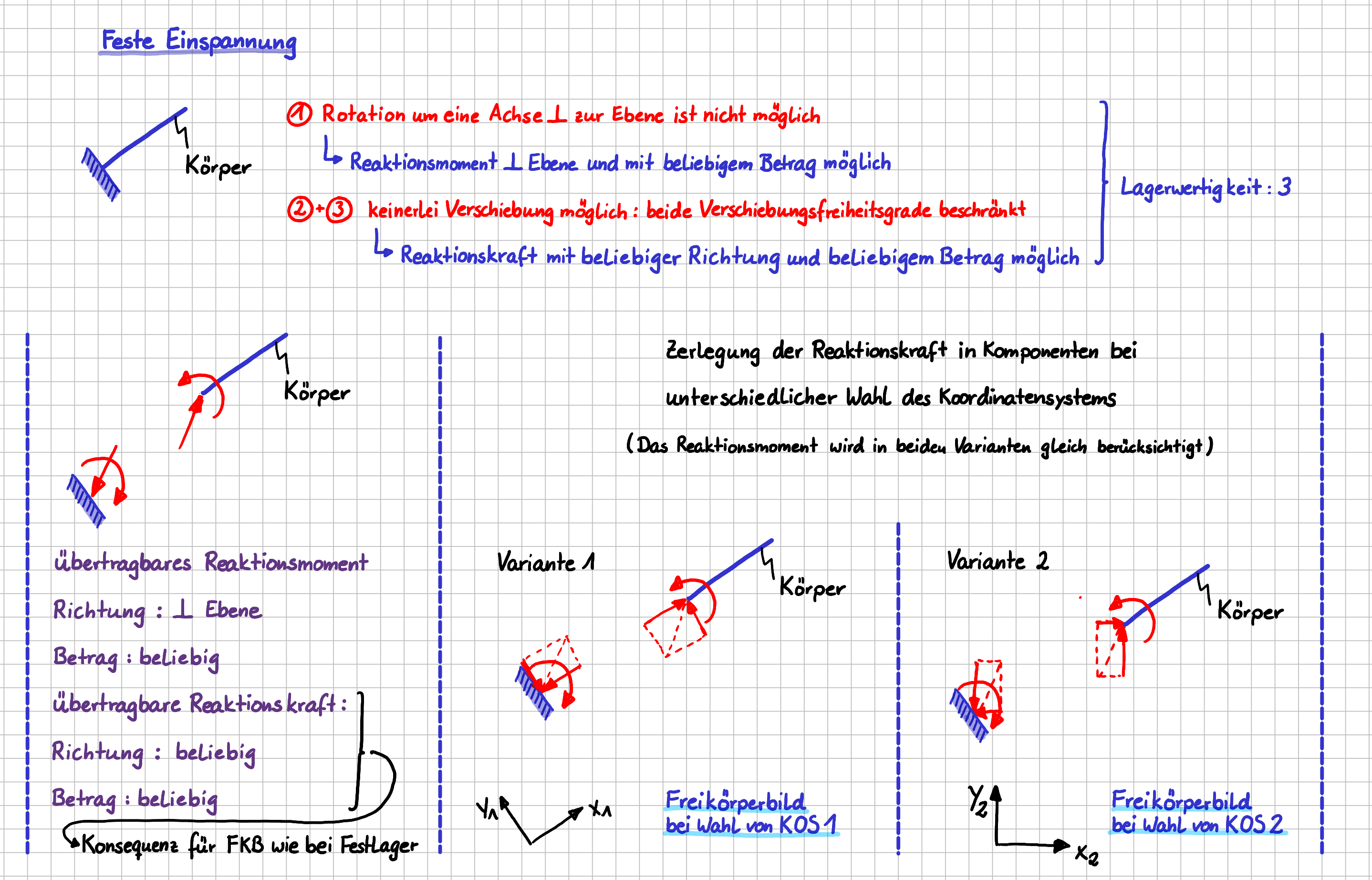
Feste Einspannung im ebenen System

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13820/mod_book/chapter/2189/Feste_Einspannung_im_ebenen_System.png

Alles, was wir uns zur Lagerkraft beim Festlager angeschaut haben, gilt natürlich auch hier: Eine feste Einspannung kann eine beliebige Reaktionskraft übertragen: Richtung und (vorzeichenbehafteter) Betrag müssen durch Auswerten der Gleichgewichtsbedingungen bestimmt werden.
Die feste Einspannung kann aber auch ein Moment übertragen. Dieses Moment wirkt um eine Achse senkrecht zur Ebene.

Physikalisch betrachtet kann eine feste Einspannung also "alles, was geht" übertragen: eine beliebige Reaktionskraft und ein Moment.

Die Reaktionskraft musst du (wie beim Festlager) durch zwei zueinander senkrechte Kraftkomponenten im Freikörperbild berücksichtigen. Typischerweise wirst du diese beiden Kraftkompoonenten in Richtung der Koordinatenachsen einzeichnen. Die Art, wie du das Reaktionsmoment beim Erstellen eines Freikörperbildes berücksichtigst, ist unabhängig von der Wahl des Koordinatensystems.

Hier kannst du dir die Inhalte des bisherigen Abschnitts noch einmal als Video anschauen:

Schauen wir uns zum Abschluss noch ein Beispiel mit einem Festlager und einem Loslager an.
Gegeben ist ein Modell eines Krans.
Die Struktur des Krans wird als Fachwerk abgebildet, das in den Punkten A und B mit einem Fest- bzw. einem Loslager wie dargestellt gelagert ist.
Als Belastung wirken zwei Kräfte mit Betrag F.

Welche Unterschiede ergeben sich im Freikörperbild und beim Aufstellen der Gleichgewichsbedingungen, wenn in Variante 1 ein Koordinatensystem mit horizontal ausgerichteter x-Achse und in Variante 2 ein Koordinatensystem mit um 45° geneigter x-Achse verwendet wird?

Erstellen eines Freikörperbildes: verschiedene Koordinatensysteme

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13820/mod_book/chapter/2189/Erstellen_eines_FKB_verschiedene_KOS.png

Beim Loslager darf es keine zwei Meinungen geben: Die Reaktionskraft wirkt senkrecht zur Bezugslinie, also senkrecht zur möglichen Verschiebungsrichtung. Das ist die Physik dieses Lager. Ausrufezeichen!
Für die mathematische Beschreibung musst du ein Koordinatensystem wählen. Wählst du das Koordinatensystem nach Variante 1, bedeutet dies also zwangsläufig, dass du die Lagerkraft in B beim Aufstellen der Gleichgewichtsbedingungen in Komponenten zerlegen musst. Wählst du ein Koordinatensystem nach Variante 2, musst du die Lagerkraft in B nicht zerlegen. Wenn wir also rein auf diese Lagerkraft schauen, ist es cleverer, das Koordinatensystem nach Variante 2 zu wählen.

Beim Freischneiden des Festlagers hast du die Wahl, wie du die "Reaktionskraft mit beliebiger Richtung und beliebigem Betrag" in Komponenten zerlegst. Es ist also naheliegend und clever, sie so zu zerlegen, dass die beiden Komponenten jeweils in die gewählten Achsrichtungen zeigen. Genau so bin ich im Beispiel auch vorgegangen. Du hast bei diesem Vorgehen dann die beiden unbekannten Kraftkomponenten, die es zu bestimmen gilt clever festgelegt, da sie in Achsrichtung zeigen und damit beim Aufstellen der Gleichgewichtsbedingen direkt für das jeweilige Kräftegleichgewicht in Achsrichtung berücksichtigt werden können.
Das Reaktionsmoment wirkt um die Achse senkrecht zur Ebene, was bei der Wahl der beiden Koordinatensystem in beiden Fällen die z-Achse ist.

Welches der beiden Koordinatensysteme nun die cleverere Wahl ist, kannst du natürlich nur beurteilen, wenn du das Gesamtsystem betrachtest. Bei Variante 1 muss nur die Lagerkraft in B beim Aufstellen der Gleichgewichtsbedingungen in Komponenten zerlegt werden, da die eingeprägten Kräfte F entlang der y-Richtung von KOS 1 zeigen. Bei Variante 2 müssen nur die beiden eingeprägten Kräfte F beim Aufstellen der Gleichgewichtsbedinungen zerlegt werden.
In diesem Fall ist also gar kein so wirklicher Unterschied zwischen dem Aufwand bei den beiden Varianten zu beobachten. Das kann bei anderen Systemen sehr anders sein.
Achte doch ab jetzt einfach mal darauf. Und überleg immer mal wieder, selbst wenn bei Aufgaben ein Koordinatensystem vorgegeben ist, ob bzw. warum das eine clevere Wahl für die Ausrichtung der Achsen gibt ... und, ob es nicht vielleicht eine cleverere Wahl gäbe.

Wenn du dich schon mit dem Aufstellen und ausrechnen von Gleichgewichtsbedingungen beschäftigt hast, rechne doch die Lagerreaktionen für das obige System einmal für beide Varianten des Freikörperbilds aus.

Ich habe das in dem folgenden Video getan und habe alle Schritte detailliert aufgeschrieben:

Ich hoffe, dass du sehr klar verstanden hast, dass es einen Unterschied zwischen der Physik und damit der Funktionsweise eines Lagers gibt (die vollkommen unabhängig von der Wahl des Koordinatensystems ist) und der Tatsache, dass du für die mathematische Beschreibung eines Systems und damit auch der Lager ein Koordinatensystem wählen musst. Bei Lagertypen, die eine beliebige Reaktionskraft übertragen können (z.B. Festlager und feste Einspannung) kannst du die beliebige Reaktionskraft gleich durch zwei Krafkomponenten berücksichtigen, die in die Richtung der gewählten Koordinatenachsen zeigen.
Je nachdem wie du das Koordinatensystem wählst, kannst du mehr oder weniger Arbeit beim Aufstellen der Gleichgewichtsbedingungen haben, da du unterschiedlich viele Kräfte in Komponenten zerlegen musst.

Zusammenfassung - Das Wichtigste in Kürze

Lager in ebenen Systemen

Im ebenen Fall hat ein Körper drei Freiheitsgrade: zwei Verschiebungen (= zwei Translationsfreiheitsgrade) und eine eine Drehung (= einen Rotationsfreiheitsgrad) um die Achse senkrecht zur Ebene, in der die Verschiebungen möglich sind.
Es sind also genau diese drei Freiheitsgrade, die von Lagern eingeschränkt werden können.

Wird eine Verschiebungsmöglichkeit durch ein Lager behindert, tritt eine Reaktionskraft im Lager auf.
Wird eine Drehung durch ein Lager behindert, tritt ein Reaktionsmoment im Lager auf.

Reaktionskräfte und -momente bezeichnet man als Reaktionsgrößen.

Es können im ebenen Fall also maximal drei Reaktionsgrößen - zwei Reaktionskräfte und ein Reaktionsmoment - in einem Lager auftreten.
Anders ausgedrückt: Die maximale Wertigkeit eines Lagers im ebenen Fall kann also drei sein.

Zusammenstellung typischer Lager und ihrer Freikörperbilder im ebenen Fall: