Wenn du dich dem Moment einer Einzelkraft noch einmal aus einem anderen Blickwinkel nähern möchtest, dann kannst du einfach eine der zulässigen Operationen für Kräfte verwenden, nämlich dass Addieren des Nullvektors.

Nehmen wir einmal an, dass dich in dem folgenden System die Momentenwirkung der Einzelkraft \(2F\) bezüglich des Punktes \(A\) interessiert ... z.B. weil du diesen Anteil brauchst, um das Momentengleichgewicht bezüglich des Punktes \(A\) aufzustellen.

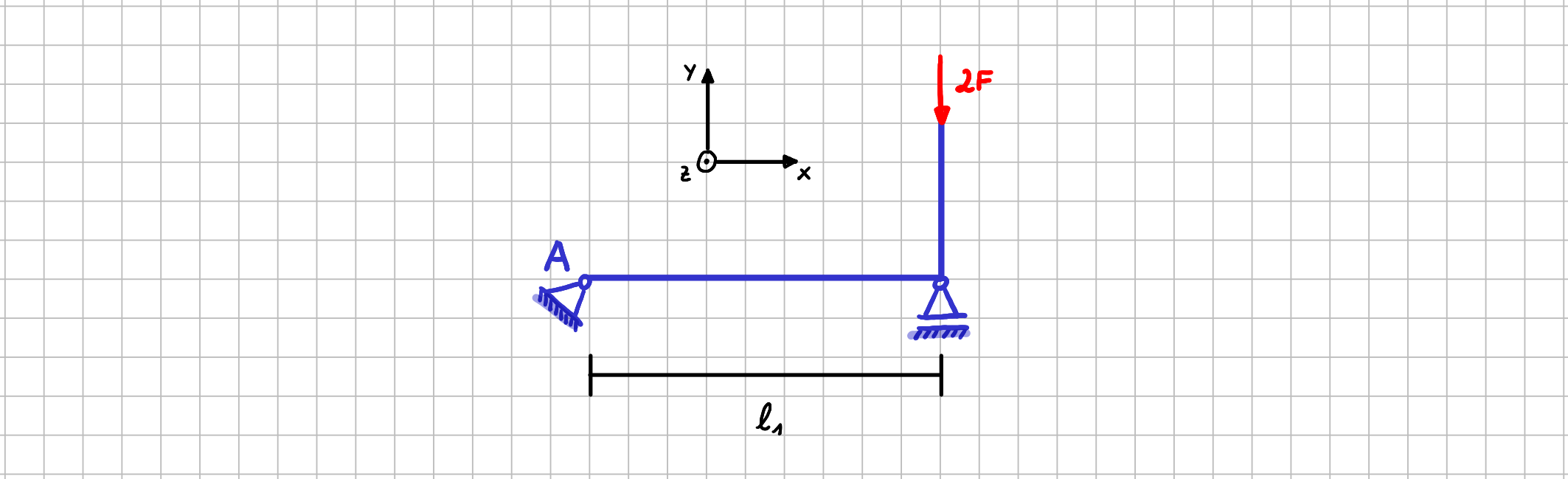
System für die Betrachtung der Momentenwirkung einer Einzelkraft mit Hilfe des Kräftepaars

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2182/System_Zusammenhang_Kraeftepaar_Momentenwirkung_Einzelkraft.png

Dann kannst du, so wie im Bild rechts dargestellt, im Punkt \(A\) einfach den Nullvektor in Form von zwei Kräften mit Betrag \(2F\) und entgegengesetzer Richtung ergänzen.

Wenn du jetzt die drei Kräfte "anders anschaust", dann siehst du, dass du eine Einzelkraft mit Betrag \(2F\) im Punkt \(A\) angreifen hast, die in dieselbe Richtung zeigt, wie die Kraft, deren Momentenwirkung du berechnen willst. Zusätzlich hast du ein Kräftepaar.
Da die Wirkungslinien der beiden Kräfte den Abstand \( \ell_a \) haben, ist der Betrag des Momentes \(2F \cdot \ell_1 \) und die Richtung ist durch den Drehsinn der beiden Kräfte vorgegeben.

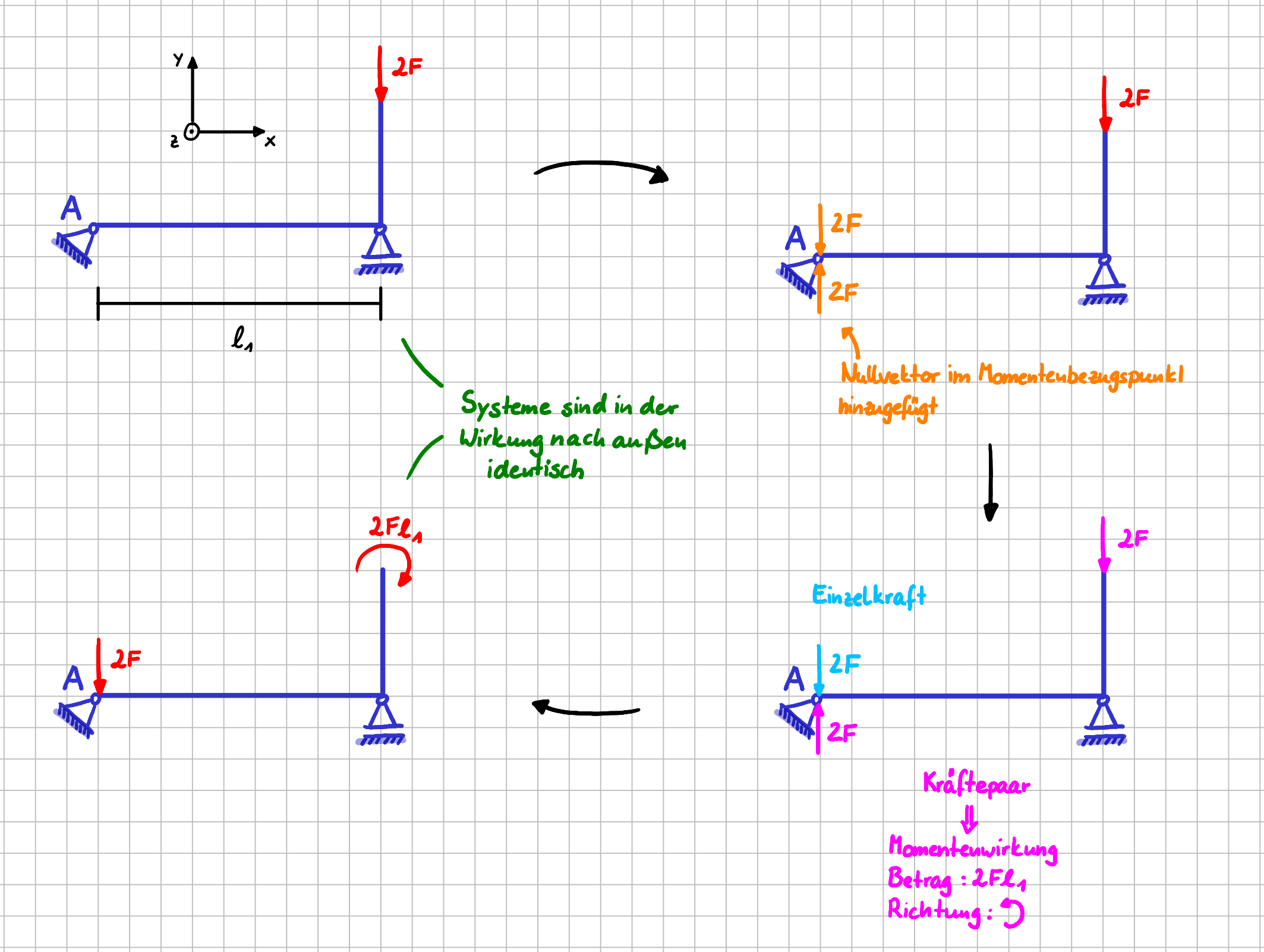
Momentenwirkung einer Einzelkraft erklärt mit Hilfe des Kräftepaars

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2182/Herleitung_Zusammenhang_Kraeftepaar_Momentenwirkung_Einzelkraft.png.png?time=1735557798481

Das Ausgangsssystem und das System, bei dem die Kraft \(2F\) im Punkt \(A\) angreift und das Einzelmoment  \(2F\ell_1\)  angreift, sind also in der Wirkung nach außen identisch.
Wo du das Moment einzeichnest, ist dabei vollkommen egal, da das Moment ein freier Vektor ist.

Durch das Einführen des Nullvektors ist mit der Ausgangskraft also ein Kräftepaar entstanden, aus dem die Momentenwirkung der Ausgangskraft "direkt" sichtbar gemacht werden kann.