Moment
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Moment |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 14:07 |
Beschreibung
1. Einleitung Moment
Einleitung Moment
In dieser Lektion nehmen wir die physikalische Größe Moment ganz genau unter die Lupe.
Das Moment ist für viele so eine Größe, die vielleicht erstmal etwas ungewohnt daherkommt. Irgendwie hat man eine Vorstellung aufgrund der eigenen Alltagserfahrung davon, was ein Moment ist. Und dann kommt da die mathematische Beschreibung ins Spiel ... und viele scheinen zu vergessen, was sie schon wissen.
Deshalb schauen wir erstmal ohne Formeln, was ein Moment eigentlich ist.
Wir schauen uns erst an, was das Moment eines Kräftepaars ist.
Dann klären wir, was die Momentenwirkung einer Einzelkraft ist.
Und na klar steigen wir auch ein in die Modellierung: Wir wollen ja versuchen, reale Systeme mathematisch zu beschreiben. Hier gibt es unterschiedliche Herangehensweisen, die aber immer nur eines zum Ziel haben: Das, was im realen System passiert, also losgelöst von irgendeiner mathematischen Beschreibung 'einfach so ist', mit Formeln greifbar zu machen, um auch Berechnungen durchführen zu können.
Aber der Reihe nach: wir starten in die beiden folgenden Kapiteln wie gesagt erstmal ganz 'unmathematisch'.

Jedes Moment kann interessant sein
Weitere Informationen
2. Moment eines Kräftepaars
Moment eines Kräftepaars
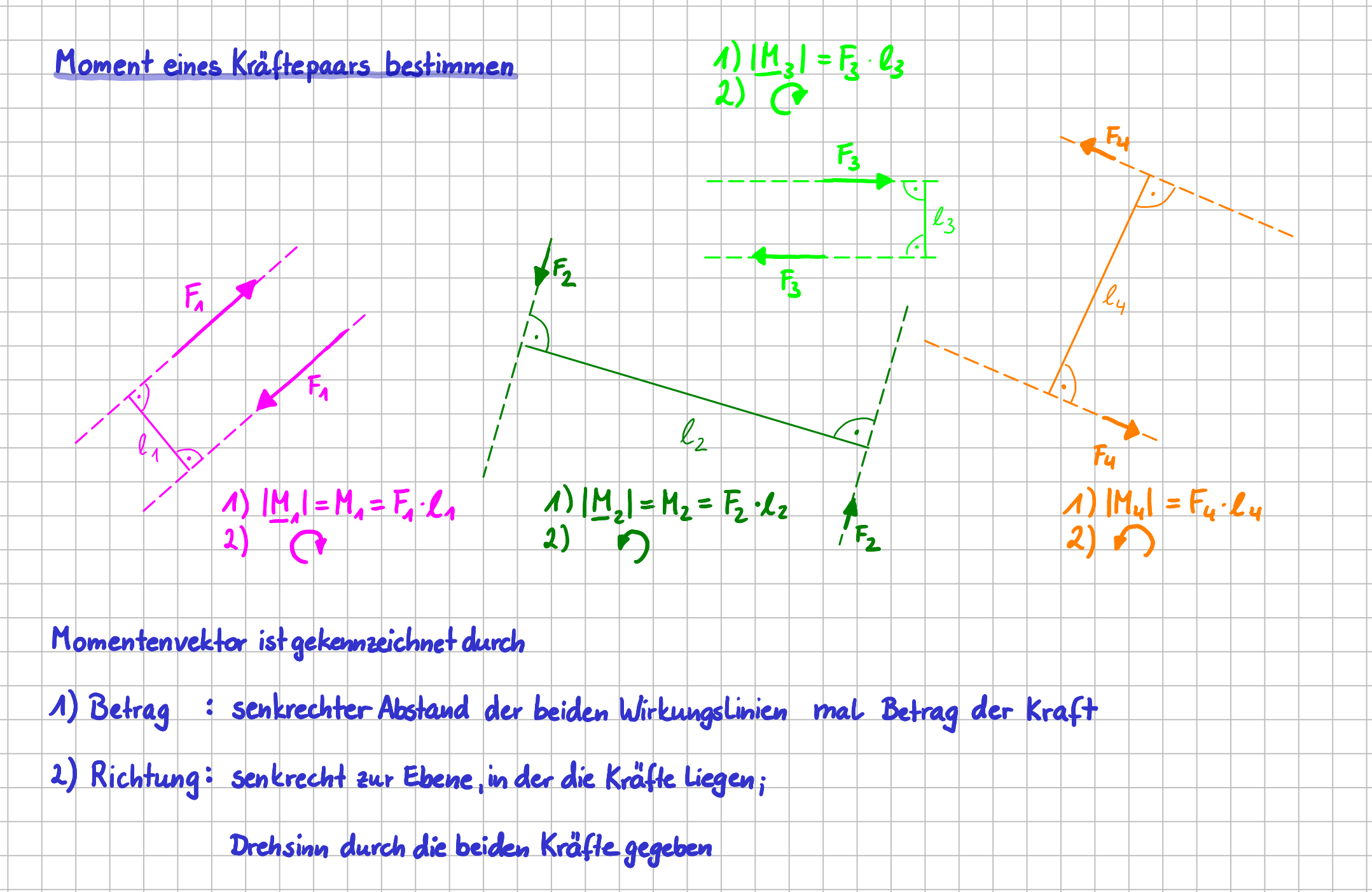
Ein Kräftepaar ist eine besondere Konstellation von Kräften.Es wirken zwei Kräfte ... da ist logisch, sonst hieße es nicht Paar. Diese beiden Kräfte haben folgende Eigenschaften.
Es sind zwei Kräfte,
- die denselben Betrag haben,
- deren Wirkungslinien parallel sind und
- deren Richtungen entgegengesetzt sind.
Vier verschiedene Kräftepaare
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2179/Vier_verschiedene_Kraeftepaare.png
Alle diese Kräftepaare haben ausschließlich eine Momentenwirkung.
Wenn dir das bis jetzt zu theoretisch ist und du es gerne ein bisschen realitätsnäher hättest, dann lies doch gleich weiter. Da geht es nämlich erstmal ganz anschaulich darum, was ein Kräftepaar ist. Und erst dann geht es an die mathematische Beschreibung.
2.1. ... mechanisch verstehen
Moment eines Kräftepaars
... mechanisch verstehen
Du hast bestimmt schon mal mit einem Schraubendreher von Hand eine Schraube angezogen, oder?
Schließ mal kurz die Augen und stell dir vor, was du beim Anziehen in der Hand, die den Schaft des Schraubendrehers hält, spürst.
Tada..... genau das, was du da wahrnimmst, ist ein Moment.
Soweit ganz einfach, oder?

Anziehen einer Schraube mit einem Schraubendreher
Weitere Informationen
Simone D. McCourtie
CC BY-NC-ND 2.0
https://www.flickr.com/photos/10816734@N03/3963500758
Und was hat das jetzt mit einem Kräftepaar zu tun?
Wir stellen uns vor, dass die Schraube schon ein Stück ins Werkstück eingeschraubt ist und dass du gerade ein so großes Moment mit deiner Hand aufbringst, dass der Schraubendreher die Schraube gerade noch nicht weiter in das Werkstück reindreht. Dann sind wir noch im Bereich der Statik. (Würdest du ein minimal größeres Moment mit deiner Hand aufbringen, käme der Schraubendreher in Bewegung und wir wären im Bereich der Dynamik.)
Das, was du mit der Hand aufbringst, ist das Moment \( M_{\mathrm{Hand}} \). Da das Moment eine Drehbewegung bewirken würde, ist es naheliegend, für das Moment einen 'gekrümmten' Pfeil zu verwenden, wie er in der Zeichnung links in grün eingezeichnet ist.
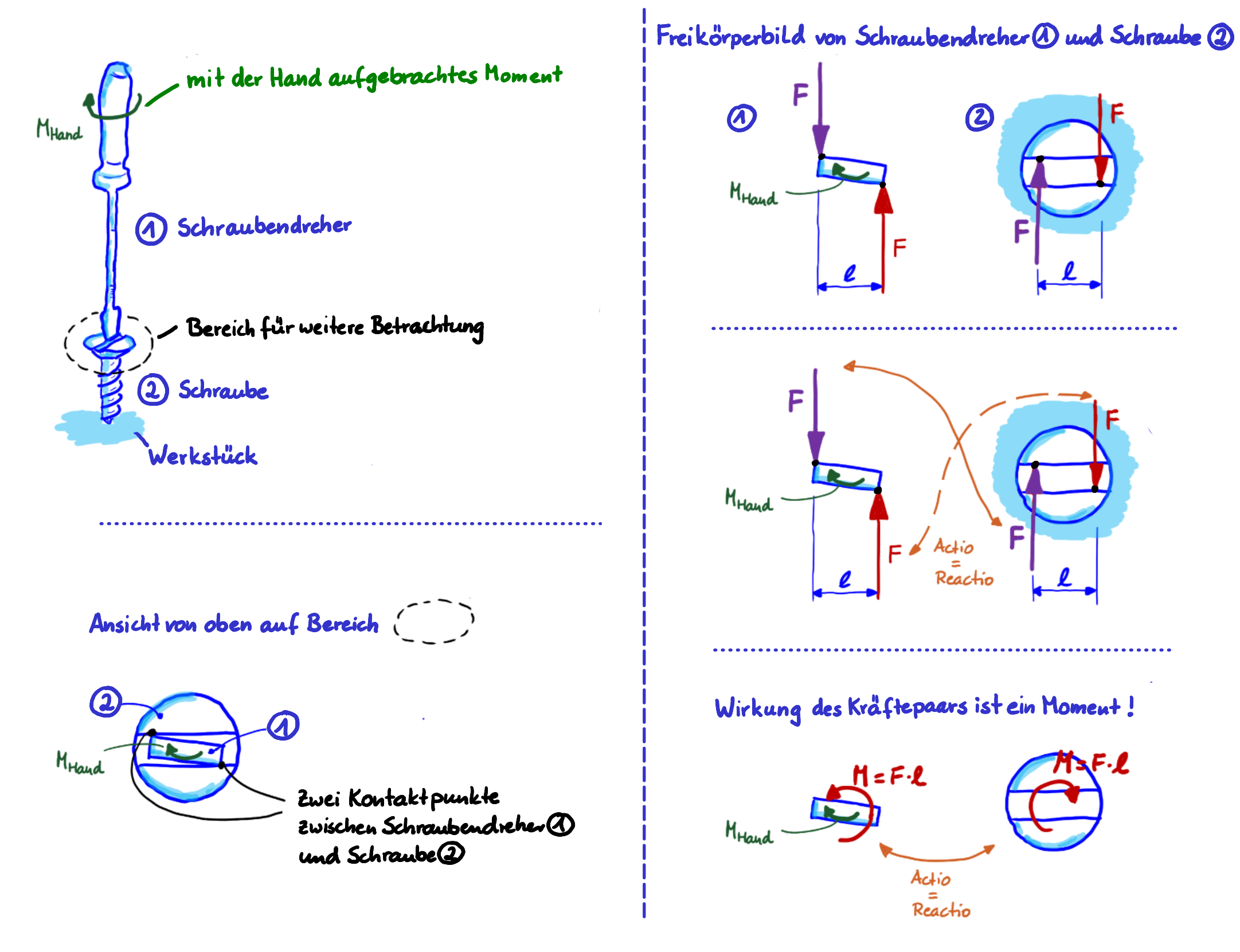
Kräftepaar und Moment beim Schlitzschraubendreher
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2174/Kraeftepaar_und_Moment_beim_Schlitzschraubendreher%20%281%29.png
Schauen wir jetzt mal genau in den Kontaktbereich zwischen Schraubendreher und Schraube. Die Schraubendreherspitze berührt den Schlitz der Schraube in genau zwei Kontaktpunkten.
Wenn wir das Gesamtsystem an dieser Stelle trennen, also ein Freikörperbild des Schraubendrehers zeichnen und auch den Schraubenkopf separat darstellen, dann wirken auf den Schraubendreher das Moment \( M_{\mathrm{Hand}} \) und zwei Kräfte mit Betrag \( F \) an den Kontaktpunkten. Die Richtung der beiden Kräfte ist senkrecht zum Schlitz und der Abstand der beiden Kontaktpunkte ist wie eingezeichnet \( \ell \).
Und da ist es, das Kräftepaar. Tada.
Da der Schraubendreher im Gleichgewicht ist \( - \) er bewegt sich ja nicht \( - \), muss die resultierende Wirkung aller angreifenden Größen ( \( M_{\mathrm{Hand}} \) und Kräfte \( F \) ) im Gleichgewicht sein.
Für die Summe aller angreifenden Kräfte, also das Kräftegleichgewicht, gilt: \( F-F=0 \).
Ein Kräftepaar hat also keine resultierende Kraftwirkung auf den Körper.
Nun wirkt ja aber nachweislich das Moment deiner Hand an dem Schraubendreher. Also muss aus dem Kräftepaar ein dem Moment \( M_{\mathrm{Hand}} \) entgegengesetzt gerichtetes Moment resultieren. Sonst könnte der Schraubendreher ja gar nicht im Gleichgewicht sein. Und genau so ist es. Für das Momentengleichgewicht gilt: \( M_{\mathrm{Hand}}=F\cdot \ell=M_{\mathrm{Kräftepaar}} \).
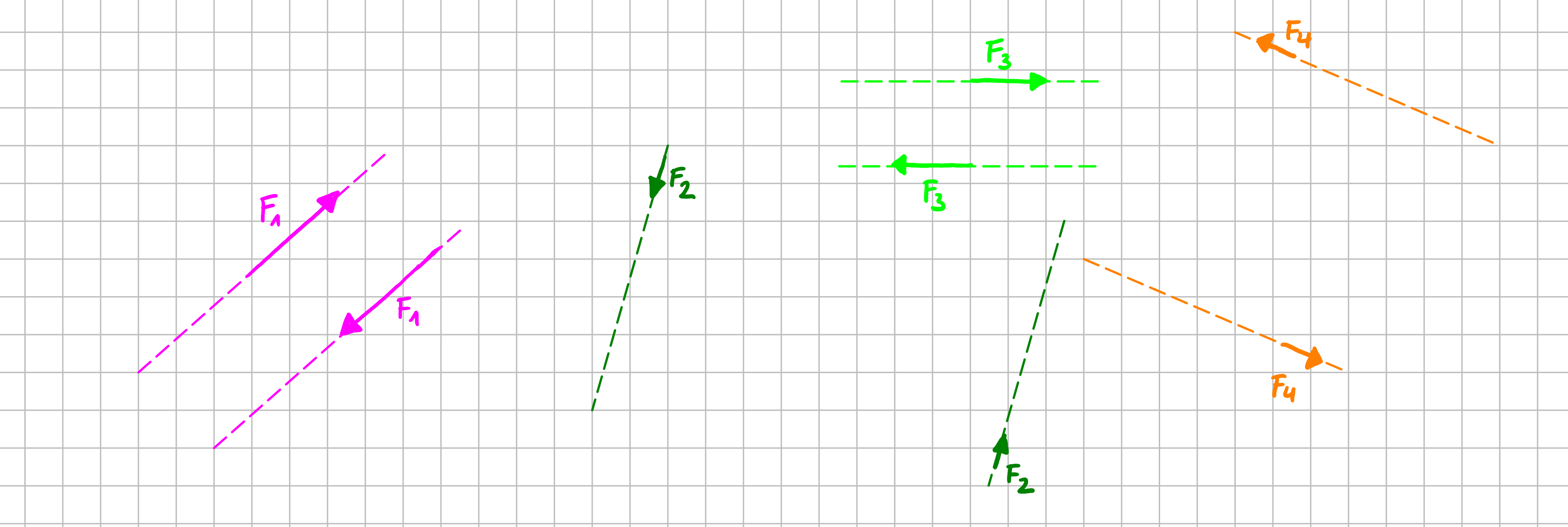
Ein Kräftepaar hat also als Wirkung auf den Körper ausschließlich ein Moment, das den Betrag "Kraft mal senkrechter Abstand der Wirkungslinien der Kräfte" hat. Seine Richtung ist durch die Richtung der Kräfte gegeben: In diesem Beispiel "drehen" die beiden Kräfte linksrum. Das Moment, das du mit der Hand aufbringst, wirkt genau andersrum.
Übertragen wir das Gelernte noch auf die vier Kräftepaare aus dem Beispiel:
Resultierende Momente für vier verschiedene Kräftepaare
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2174/resultierende_Momente_fuer_vier_verschiedene_Kraeftepaare.png
Zusammenfassung - Das Wichtigste in Kürze
Ein Kräftepaar ist gekennzeichnet durch zwei Kräfte,
- die denselben Betrag haben,
- deren Wirkungslinien parallel sind und
- deren Richtungen entgegengesetzt sind.
Das Moment eines Kräftepaars ist - wie jeder Momentenvektor - gekennzeichnet durch seinen Betrag und seine Richtung:
- Betrag = 'senkrechter Abstand zwischen den Wirkungslinien der beiden Kräfte mal Betrag der Kraft'
- Richtung = 'senkrecht zu der Ebene, in der das Kräftepaar liegt und mit 'Drehsinn' gemäß dem Kräftepaar'
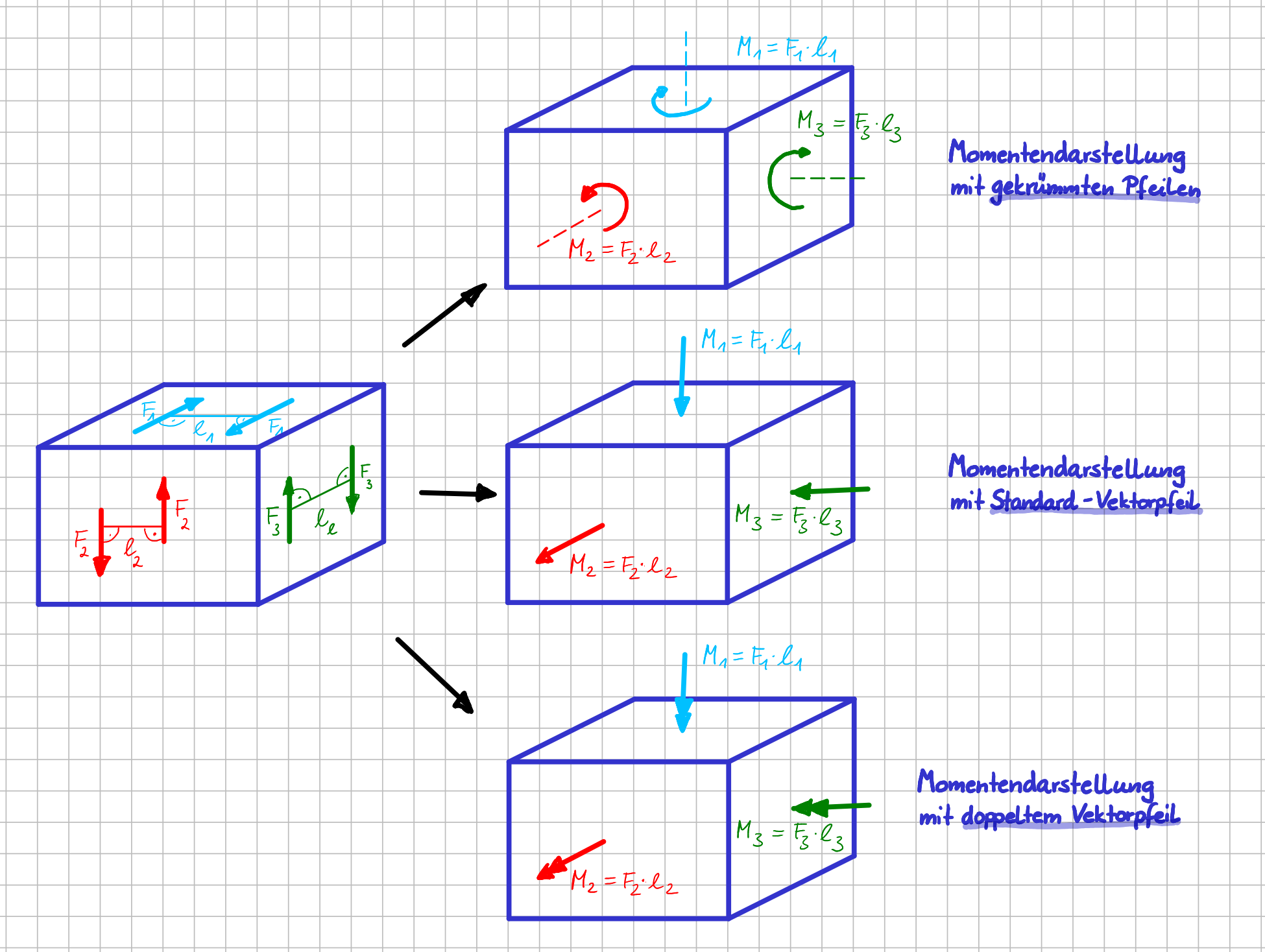
Kräftepaare und resultierende Momente mit unterschiedlichen Darstellungsarten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2174/Kraeftepaare_und_Momente_verschiedene_Darstellungsformen.png
Arbeitsblatt - Teste dein Wissen
Test - Prüfe dein Wissen
2.2. ... mathematisch darstellen
Moment eines Kräftepaars
... mathematisch darstellen
Mit dem mechanischen Verständnis aus dem vorangegangenen Abschnitt im Gepäck weißt du ja schon, in welche Richtung der Vektor zeigt und welchen Betrag er hat. Wenn es jetzt also darum geht, den Vektor mathematisch zu beschreiben, musst du diese Informationen nur noch als Vektor bezüglich eines Koordinatensystems darstellen.Wichtig ist: erst jetzt benötigst du ein Koordinatensystem. Alle Überlegungen zum mechanischen Verständnis haben wir komplett ohne Verwendung eines Koordinatensystems ausgeführt.
Machen wir es gleich konkret und greifbar. Wenn wir für das letzte Beispiel die Momentenvektoren der drei Kräftepaar mathematisch darstellen wollen, brauchen wir als erste ein Koordinatensystem. Dies ist in der folgenden Abbildung bereits eingezeichnet. Grundsätzlich kannst du dir Koordinatensystem wählen, so wie "du lustig bist". An der Mechanik ändert sich dadurch gar nichts. Einzig und allein die mathematische Darstellung kann, je nach gewähltem Koordinatensystem- einfacher oder schwieriger sein.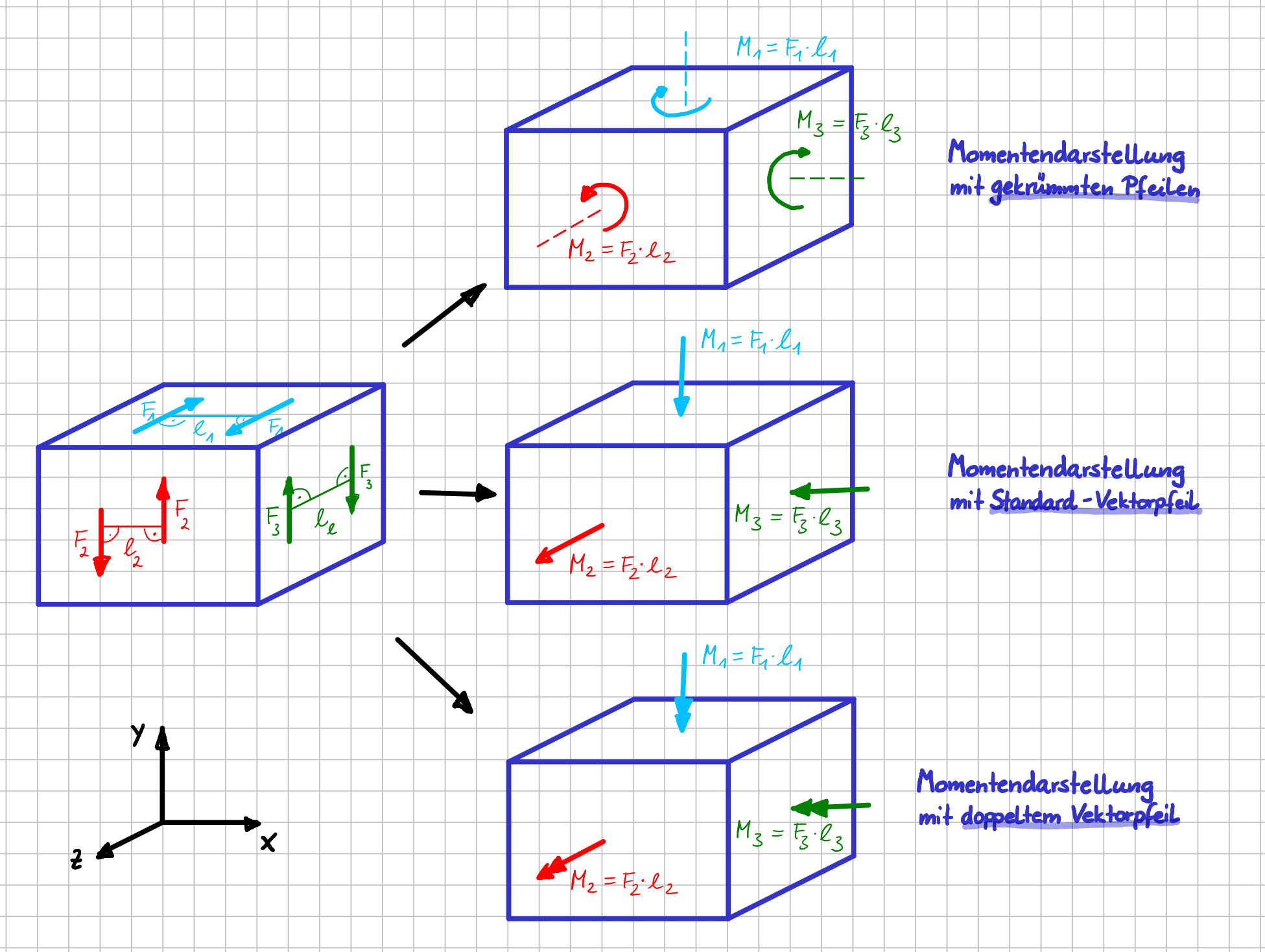
Mathematische Beschreibung der Momentenvektoren dreier verschiedener Kräftepaare
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2175/Kraeftepaare_und_resultierende_Momente_unterschiedliche_Darstellungsarten.png
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_1 \) zeigt in negative \( y \)-Richtung und hat den Betrag \( M_1=\ell_1 \cdot F_1 \). Die Vektordarstellung lautet also:
$$\vec{M}_1= \ell_1 \cdot F_1 \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ - \ell_1 F_1 \\ 0 \end{pmatrix}$$
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_2 \) zeigt in positive \( z \)-Richtung und hat den Betrag \( M_2=\ell_2 \cdot F_2 \). Die Vektordarstellung lautet also:
$$\vec{M}_2= \ell_2 \cdot F_2 \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \ell_2 F_2\end{pmatrix}$$
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_3 \) zeigt in negative \( x \)-Richtung und hat den Betrag \( M_3= \ell_3 \cdot F_3 \). Die Vektordarstellung lautet also:
$$\vec{M}_3= \ell_3 \cdot F_3 \begin{pmatrix} -1\\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -\ell_3 F_3 \\ 0 \\ 0 \end{pmatrix}$$
Und was passiert, wenn du ein anderes Koordinatensystem wählst, z.B. das lila-farbene?
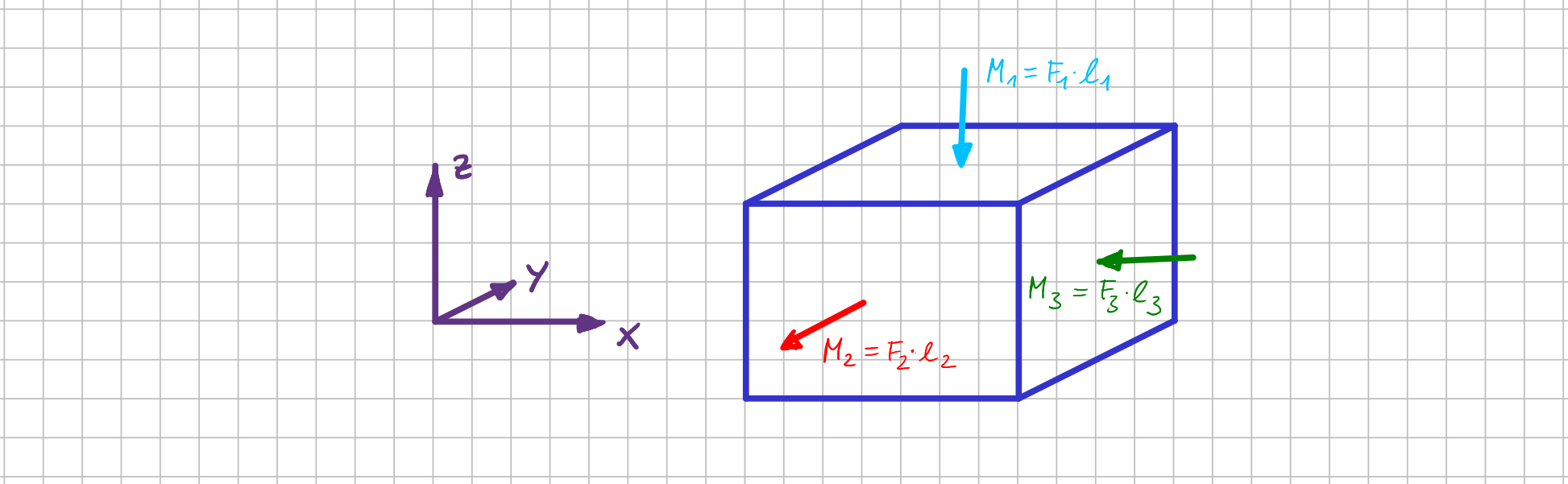
Anderes Koordinatensystem als Basis für die Darstellung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2175/Anderes_Koordinatensystem_als_Basis_fuer_die_Darstellung.png
Am mechanischen Verständnis des Momentes eines Kräftepaars und auch an der physikalischen Richtung des Momentenvektors ändert sich dadurch natürlich gar nichts. Lediglich die mathematische Darstellung ist eine andere.
Es gilt dann:
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_1 \) zeigt in negative \( z \)-Richtung und hat den Betrag \( M_1= \ell_1 \cdot F_1 \). Die Vektordarstellung lautet also:
$$\vec{M}_1= \ell_1 \cdot F_1 \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -\ell_1 F_1 \end{pmatrix}$$
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_2 \) zeigt in negative \( y \)-Richtung und hat den Betrag \( M_2= \ell_2 \cdot F_2 \). Die Vektordarstellung lautet also:$$\vec{M}_2= \ell_2 \cdot F_2 \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ - \ell_2 F_2 \\ 0 \end{pmatrix}$$
Beim Moment des Kräftepaars mit den Kräften \( \vec{F}_3 \) ändert sich nichts, da die Ausrichtung der lila-farbenen und der schwarze \( x \)-Achse identisch ist:
$$\vec{M}_3= \ell_3 \cdot F_3 \begin{pmatrix} -1\\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -\ell_3 F_3 \\ 0 \\ 0 \end{pmatrix}$$
Mit dem mechanischen Verständnis im Kopf, ist die mathematische Beschreibung also 'nur noch' ein Hinschreiben der Vektoren mit Bezug auf das gewählte Koordinatensystem.
Arbeitsblatt - Trainiere deine Fähigkeiten
Test - Prüfe dein Wissen
3. Moment einer Einzelkraft
Moment einer Einzelkraft
Wie du in dem vorangegangenen
Abschnitt gesehen hast, ist die Wirkung eines Kräftepaars durch sein
Moment gegeben.
Die resultierende Kraft hingegen verschwindet.
Bleibt die Frage: Wie sieht das bei einer einzelnen Kraft aus?
Die
resultierende Kraft einer Einzelkraft ist die Kraft selbst. Da kann
nichts verschwinden. Das ist offensichtlich.
Aber was ist mit der
Momentenwirkung einer Kraft?
Irgendwas ist da anders als beim
Kräftepaar, oder?
Also: auf geht's. Schau dir
zuerst an, wie du dich der Thematik rein über das mechanische
Verständnis nähern kannst.
Und erst danach geht es wieder um die mathematische
Beschreibung.
3.1. ... mechanisch verstehen
Moment einer Einzelkraft
... mechanisch verstehen
Bestimmt hast du schon mal "Moment ist gleich Hebelarm mal Kraft" gehört. Diese Aussage ist genau dann richtig, wenn 'Hebelarm' als Kurzform von "senkrechter also kürzester Abstand zwischen der Wirkungslinie der Kraft und Bezugspunkt bzgl. dessen das Moment bestimmt wird" verstanden wird, 'Moment' als Kurzform für "Betrag des Momentes" und 'Kraft' als Kurzform von "Betrag der Kraft".
Damit das ganze übersichtlich wird, findest du hier Kurz- und Langform nebeneinander:

Bestimmung des Betrags des Momentes einer Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Bestimmung_des_Betrags_des_Moments_einer_Einzelkraft.png
Klingt kompliziert?
Wenn nein, umso besser.
Wenn ja, dann immer mit der Ruhe. Wir schauen uns das Schritt für Schritt an.
In jedem Fall haben wir schon mal eine sehr präzise Aussage für die Bestimmung des Betrags des Moments. Die gilt es jetzt zu verstehen. Und dann brauchen wir auch noch eine Aussage dazu, wie man die Richtung des Momentes einer Einzelkraft bestimmt.
Also ... irgendwie scheint schon mal klar zu sein, dass die Momentenwirkung einer Einzelkraft davon abhängt, bezüglich welchen Punktes man schaut.
Stellt sich die Frage: hat eine Einzelkraft überhaupt immer eine Momentenwirkung?
Es kommt darauf an......
In der nächsten Abbildung ist ein System bestehend aus einem Winkel und einem Los- und einem Festlager gezeigt. An ihm greifen die Kräfte \( \vec{F}_1\) und \(\vec{F}_2 \) wie dargestellt an. In der Darstellung rechts sind zusätzlich noch die Wirkungslinien der beiden Kräfte eingezeichnet.
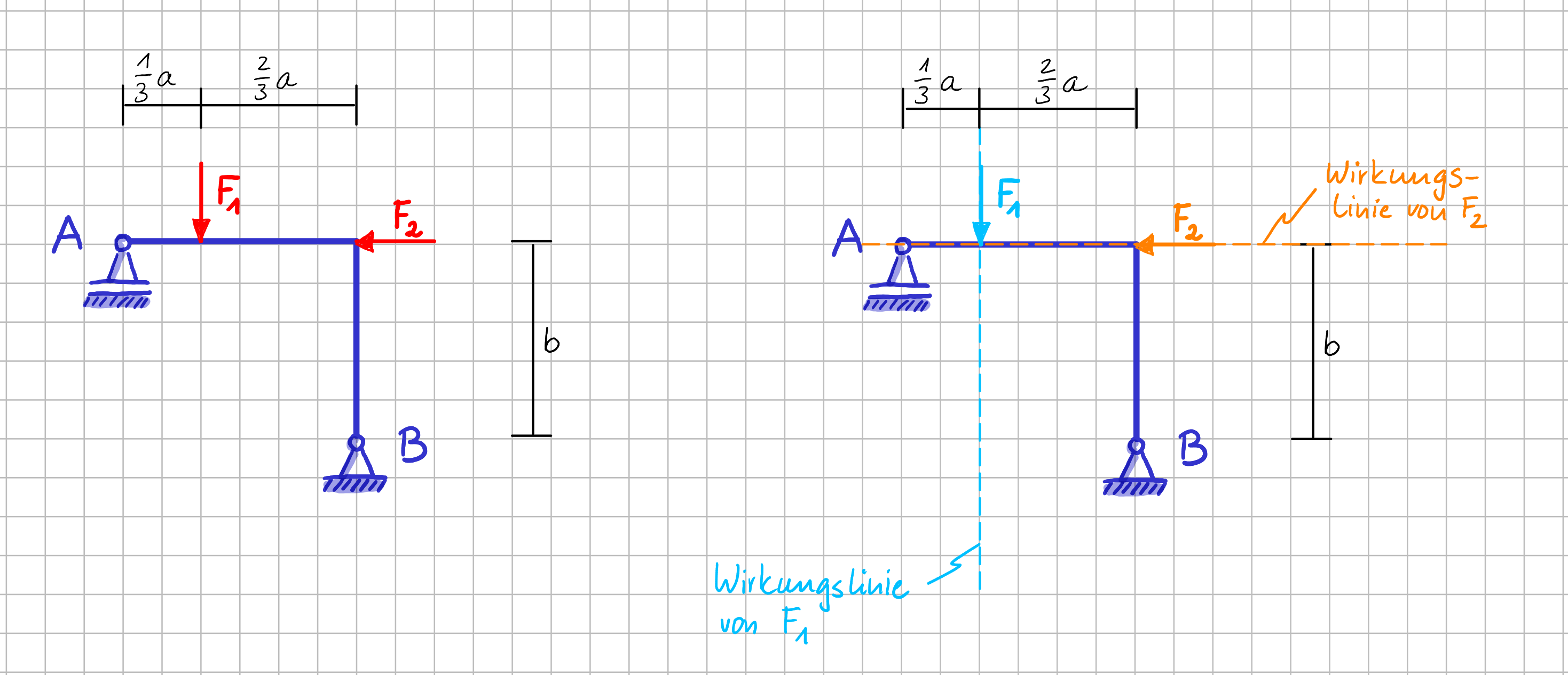
Ebenes System zur Veranschaulichung der Momentenwirkung einer Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Ebenes_System_Moment_Einzelkraft.png
Dir fällt bestimmt auf, dass kein Koordinatensystem gegeben ist. Das brauchen wir in diesem Abschnitt ja auch gar nicht, da wir erstmal auf der mechanischen Ebene verstehen wollen, was los ist.
Fangen wir mit der Kraft \( \vec{F}_2 \) an.
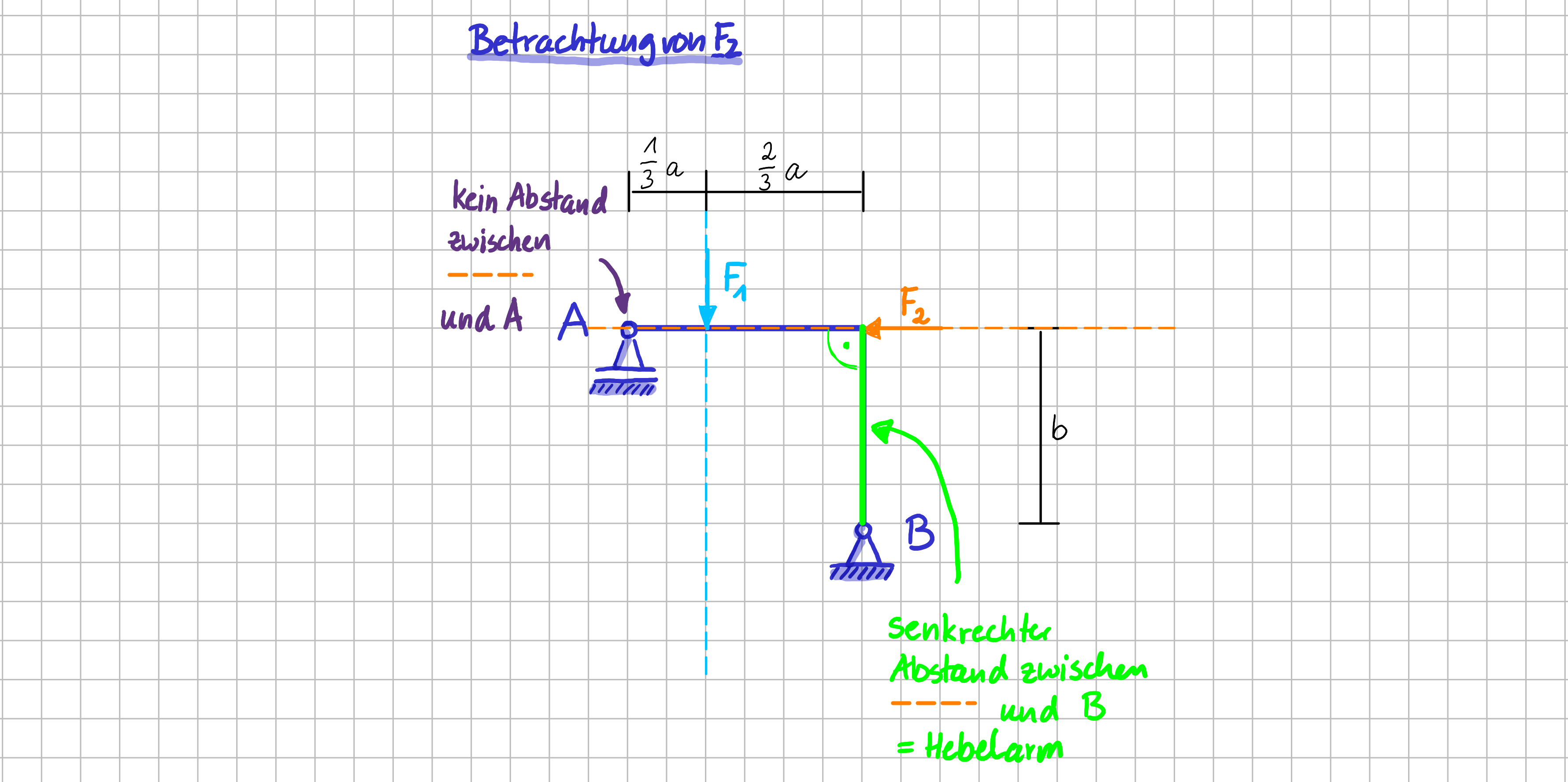
Betrachtung der Momentenwirkung der beiden Kräfte im Detail: \(\vec{F}_2\)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Betrachtung_Momentenwirkung_im_Detail.png
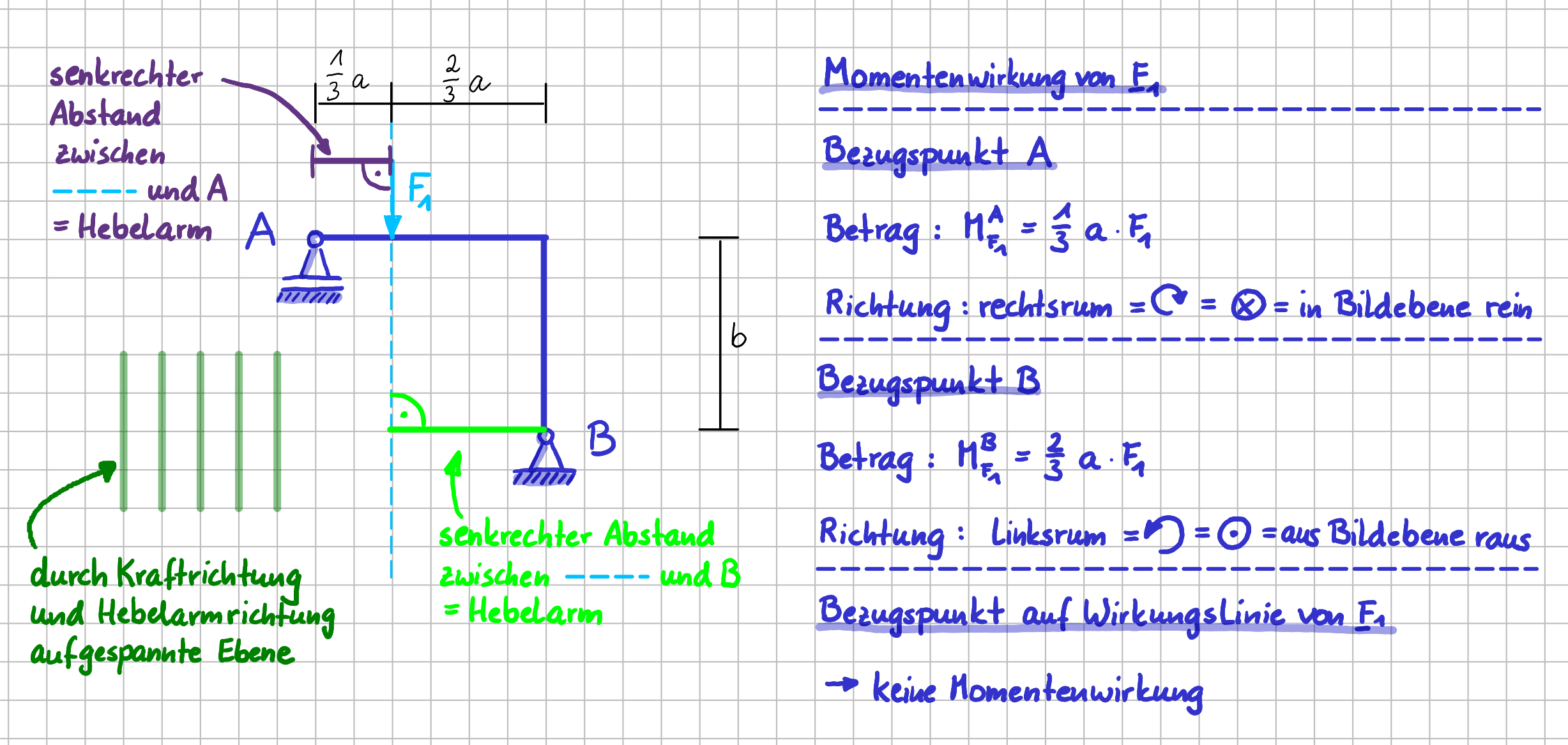
Die Momentenwirkung einer Kraft hängt von der Wahl des Bezugspunktes ab. Die Wirkungslinie der Kraft \( F_2 \) geht zum Beispiel durch den Punkt \( A \). Wenn wir also fragen "Hat die Kraft \( F_2 \) bzgl. des Punktes \( A \) einen Momentenwirkung?", so lautet die Antwort 'Nein'. Der Hebelarm, also der senkrechte Abstand zwischen Wirkungslinie der Kraft und Bezugspunkt, ist Null: Wie soll da ein Abstand sein, wenn die Wirkungslinie durch den Punkt geht?
Fragen wir "Hat die Kraft \( \vec{F}_2 \) bzgl. des Punktes \( B \) einen Momentenwirkung?", so lautet die Antwort 'Ja'. Mit diesem Bezugspunkt sieht die Welt anders aus: es gibt einen senkrechten Abstand zwischen Wirkungslinie der Kraft \( \vec{F}_2 \) und Bezugspunkt \( B \). Der Hebelarm ist die Strecke \(b\).
Für den Betrag des Momentes der Kraft \( \vec{F}_2 \) bezüglich Punkt \( B \) gilt also: \( M_2^B = b \cdot F_2 \)
Und wie sieht es mit der Richtung des Momentes aus? Die lässt sich ganz einfach bestimmen.
Stell dir vor, der Bezugspunkt \(B\) und die Wirkungslinie der Kraft \( F_2 \) sind wirklich physikalisch mit einem Balken verbunden. Dieser gedachte Balken ist im Bezugspunkt \(B\) drehbar gelagert. In welche Richtung würde die Kraft \( \vec{F}_2 \) den Balken um den Bezugspunkt \( B \) drehen wollen? Deine Antwort lautet 'linksrum', oder? Damit hast du schon die Richtung des Momentes gefunden.
Was jetzt kommt ist klar, oder? Wir schauen uns die Kraft \( \vec{F}_1 \) an.
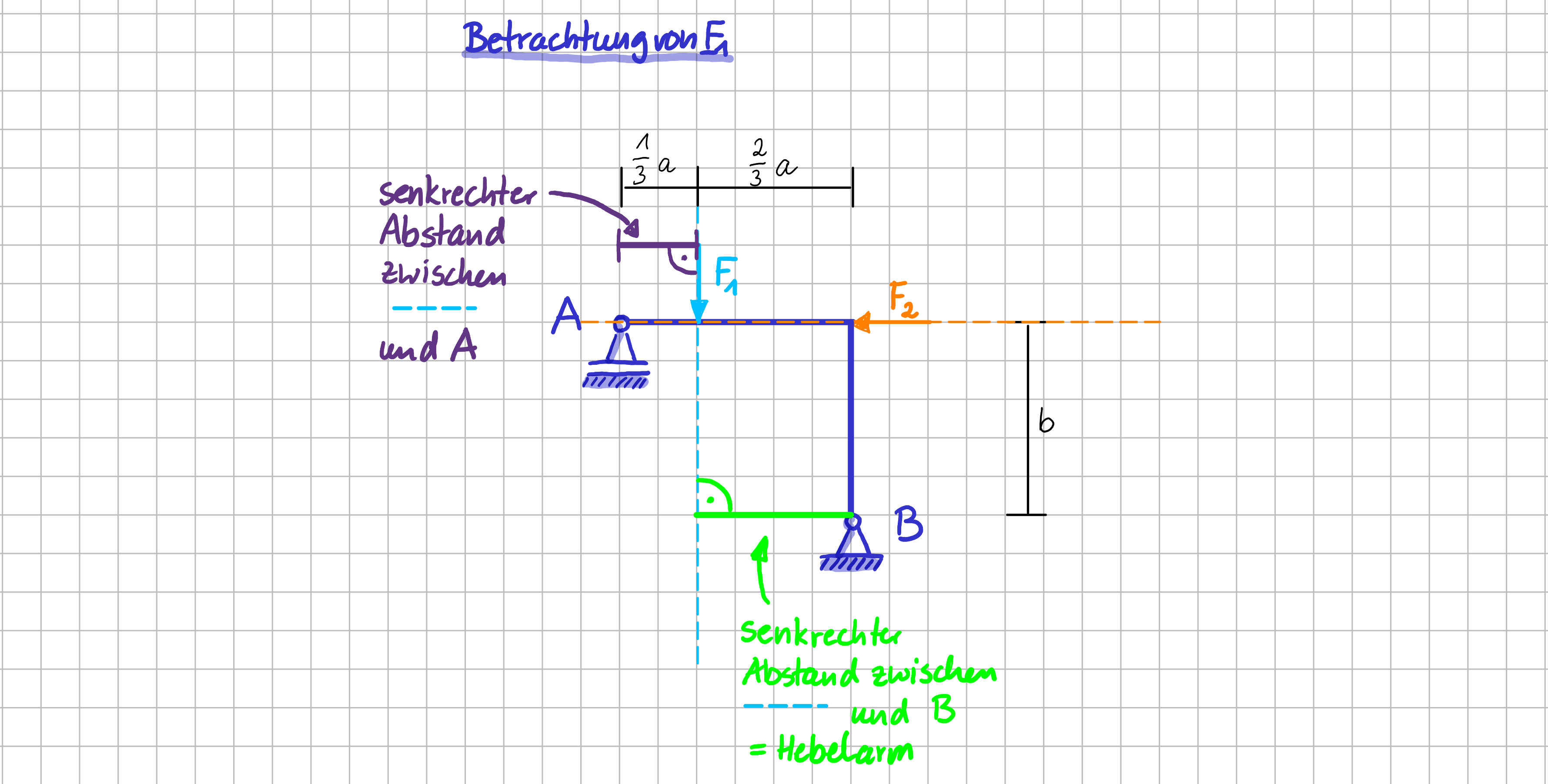
Betrachtung der Momentenwirkung der beiden Kräfte im Detail: \(\vec{F}_1\)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Betrachtung_Momentenwirkung_im_Detail_02.png
Bezüglich des Punktes \( A
\) hat die Kraft \( F_1 \) den senkrechten Abstand \( \frac{1}{3}a \). Der Betrag des Momentes der Kraft \( F_1 \) bzgl. des Punktes \( A \) ist also: \( M_1^A = \frac{1}{3}a \cdot F_1 \).
Und wie sieht es mit der Richtung des Momentes aus? Stell dir wieder vor, dass der Bezugspunkt, hier \( A \), mit einem Balken, der die Länge des Hebelarms hat, mit der Wirkungslinie der Kraft \( F_1 \) verbunden ist. In welche Richtung würde die Kraft diesen Balken drehen wollen? Jetzt lautet die Antwort 'rechtsrum'.
Und wie sieht es aus, wenn Punkt \( B \) als Bezugspunkt gewählt wird? Bezüglich des Punktes \( B \) hat die Kraft \( F_1 \) den senkrechten Abstand \( \frac{2}{3}a \). Der Betrag des Momentes der Kraft \( F_1 \) bzgl. des Punktes \( B \) ist also: \( M_1^A = \frac{2}{3}a \cdot F_1 \).
Und wie sieht es mit der Richtung des Momentes aus? Stell dir wieder vor, dass der Bezugspunkt, jetzt \( B \), mit einem Balken, der die Länge des Hebelarms hat, mit der Wirkungslinie der Kraft \( F_1 \) verbunden ist. In welche Richtung würde die Kraft diesen Balken drehen wollen? Jetzt lautet die Antwort 'linksrum'.
Für die Richtung des Momentes einer Einzelkraft können wir an dieser Stelle noch einige weitere Punkte ableiten:
Der Momentenvektor steht immer senkrecht auf der Ebene, die durch die Richtung der Kraft und die Richtung eines Verbindungsvektors zwischen Bezugspunkt und Wirkungslinie aufgespannt wird. In den betrachteten Beispielen ist diese Ebenennormale senkrecht zur Bildfläche. In welche Richtung entlang der Normalen der Ebene der Momentenvektor zeigt \(-\) raus aus der Ebene oder rein \(-\), lässt sich mit der Rechten-Hand-Regel für Momente prüfen.
Schritt 1: Faust der rechten Hand in Momentenbezugspunkt legen
Schritt 2: Daumen in Richtung der Normalen der Ebene ausstrecken (hier gibt es zwei Möglichkeiten).
Die Daumenrichtung ist identisch der Momentenrichtung, wenn die restlichen Finger in Richtung der betrachteten Kraft zeigen (und nicht entgegengesetzt).
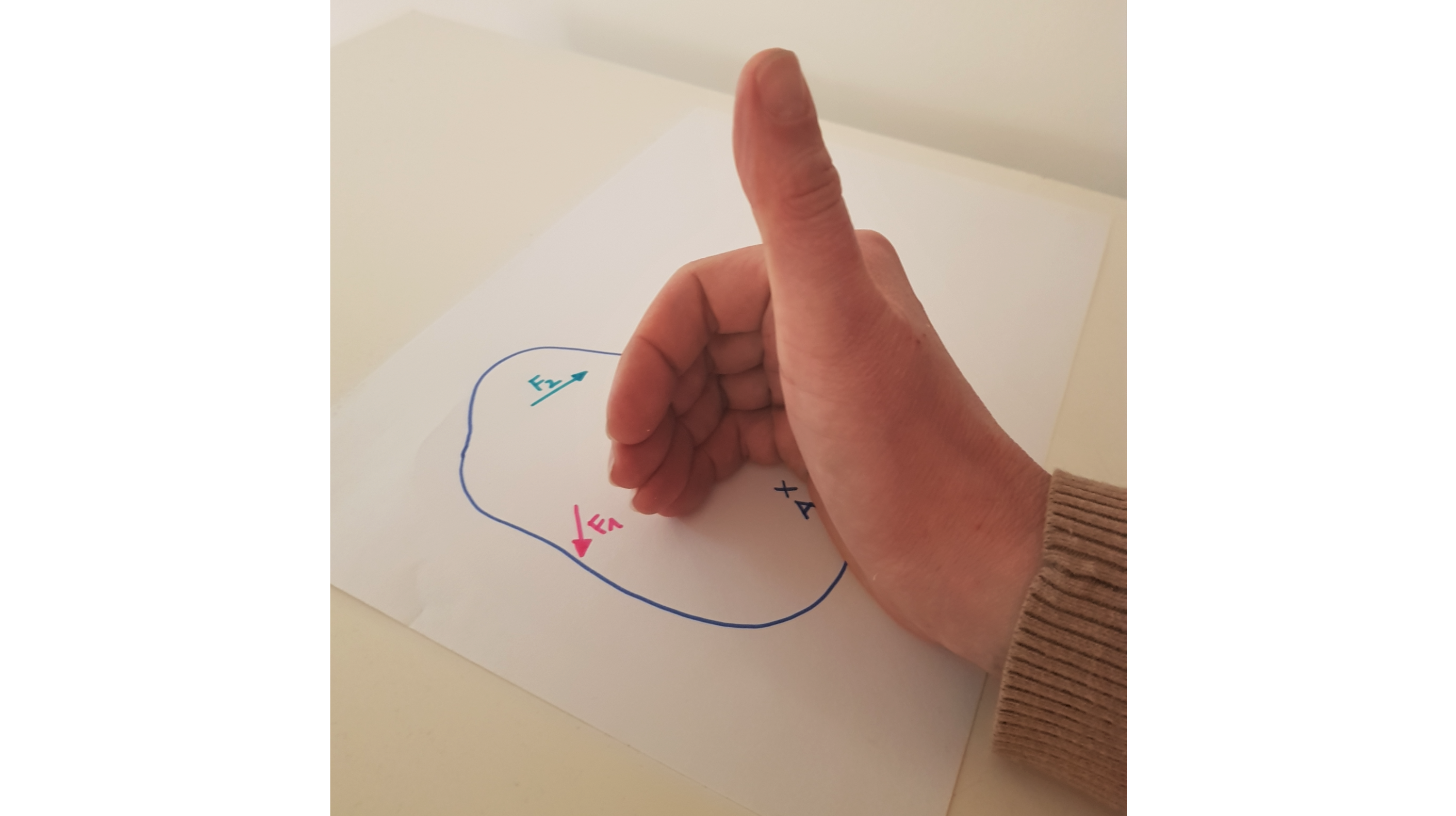
Im folgenden Beispiel soll die Momentenwirkung der beiden Kräfte \( \vec{F}_1\) und \( \vec{F}_2 \) bezüglich des Bezugspunktes \( A \) betrachtet werden. Die rechte Hand befindet sich daher im Bezugspunkt \( A \). Es geht 'nur' darum, die Richtung rauszufinden.
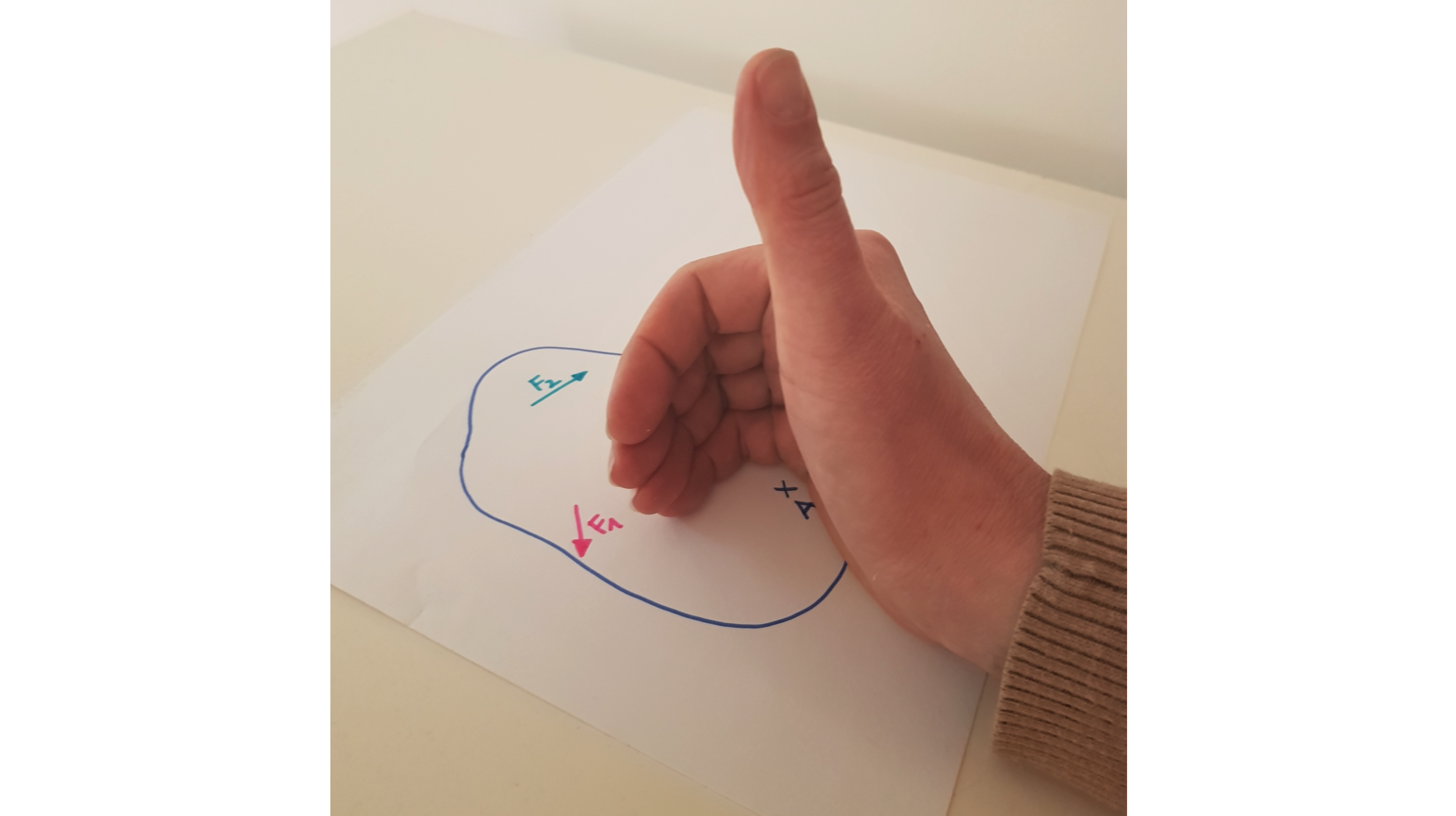
Anwenden der Rechte-Hand-Regel für das Moment zur Bestimmung der Momentenrichtung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Rechte_Hand_Regel_Momentenrichtung.png
Die beiden Kräfte liegen in der Tischebene. Es ist bereits klar, dass die Momente dieser Kräfte entweder senkrecht nach oben, oder senkrecht nach unten zeigen. Mit der Rechte-Hand-Regel kannst du schnell feststellen, dass das Moment der Kraft \( \vec{F}_1 \) senkrecht nach oben zeigt: Die Kraft \( \vec{F}_2 \) zeigt in Richtung der restlichen Finger, also ist die Momentenrichtung durch die Richtung des Daumens gegeben. Nach derselben Argumentation zeigt das Moment der Kraft \( \vec{F}_2 \) senkrecht nach unten.
Anhand der Betrachtung in diesem Abschnitt ist dir hoffentlich klargeworden, dass
- eine Einzelkraft eine Momentenwirkung haben kann,
- diese Momentenwirkung \( - \) in Bezug auf Richtung und Betrag\( - \) von der Wahl des Bezugspunktes abhängt und
- es eigentlich ganz einfach ist, Betrag und Richtung rauszufinden, wenn du wie oben beschrieben systematisch vorgehst.
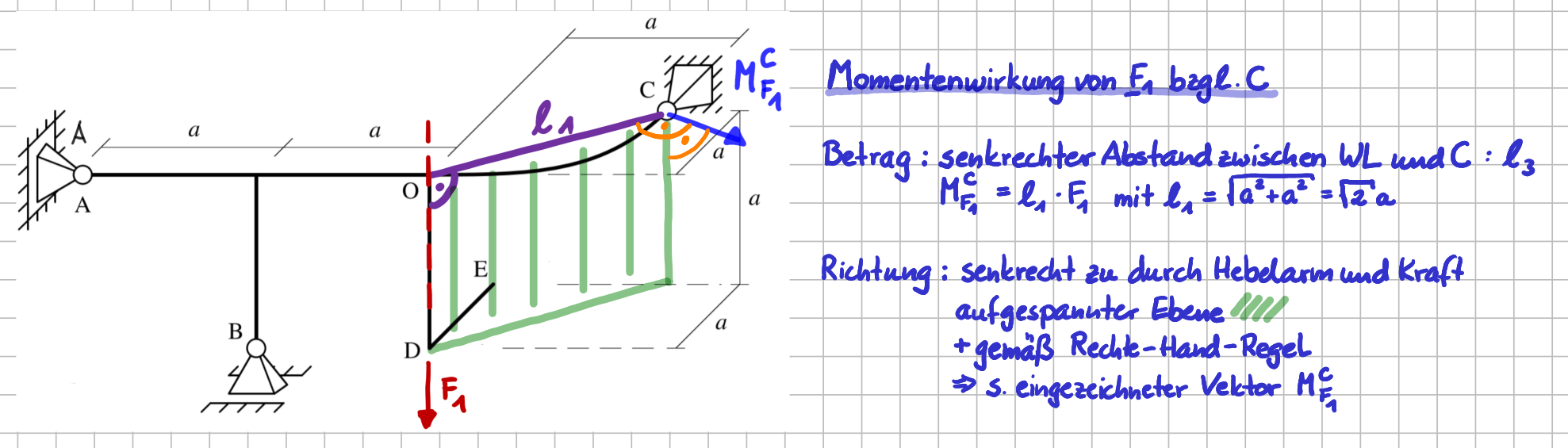
Anhand des räumlichen Systems in der nächsten Abbildung ist geprüft worden, für welche Punkte \(A\), \(B\), \(C\), \(D\), \(O\) und \(H\) die drei Einzelkräfte keine Momentenwirkung haben. Das gilt natürlich für alle Punkte, die auf der Wirkungslinie der jeweiligen Kraft liegen. Von daher sind die beiden genannten Punkte jeweils nur zwei Beispiele.
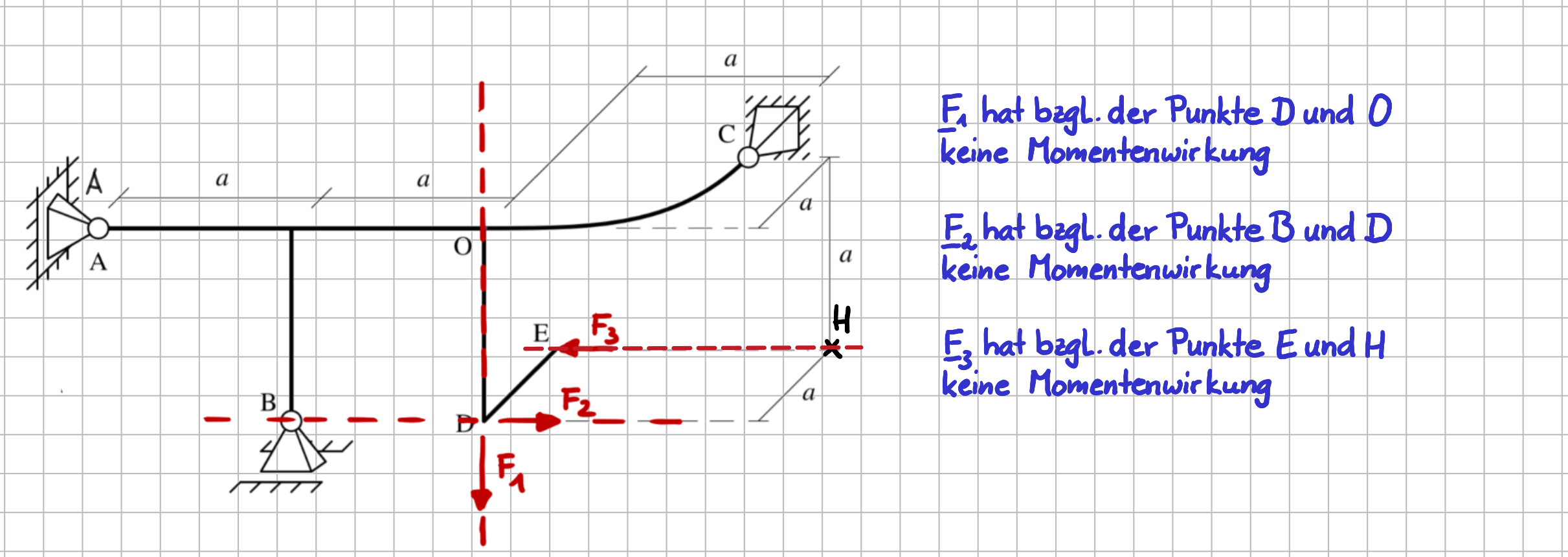
Verschwindende Momentenwirkung für den räumlichen Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/verschwindende_Momentenwirkung_raeumlicher_Fall.png
Exkurs zum Thema Gleichgewichtsbedingungen
Wichtig ist, dass du dir immer vergegenwärtigst, dass du beim Aufstellen des Momentengleichgewichts einen beliebigen Bezugspunkt wählen kannst. Es ist vom Grundsatz her vollkommen egal, welchen Bezugspunkt du nimmst. Wirklich. Es kann ein Punkt sein, der geometrisch auf einem Körper des Systems liegt. Es kann aber auch ein Punkt sein, der 'irgendwo in der Botanik' liegt, wie das z.B. beim Punkt \( H \) der Fall ist. Obwohl es theoretisch unendlich viele mögliche Bezugspunkte gibt, die du beim Aufstellen des Momentengleichgewichts wählen kannst, gibt es natürlich clevere und nicht so clevere Punkte. Clevere Punkte sind solche, durch die die Wirkungslinien möglichst vieler (unbekannter) Kräfte gehen. Bei der Wahl eines solchen Punktes reduziert sich die erforderliche Schreib- und Denkarbeit, da all diese Kräfte aufgrund des verschwindenden Hebelarms nicht ins Momentengleichgewicht eingehen.
Auch im räumlichen Fall lässt sich die Aufgabe, den Vektor der Momentenwirkung einer Einzelkraft bezüglich eine Bezugspunktes zu bestimmen, in zwei Teilschritte zerlegen:
- Bestimmung des Betrags und
- Bestimmung der Richtung des Momentenvektors.
In der folgenden Abbildung ist genau dieses Vorgehen für die drei Kräfte und je einen Bezugspunkt durchgeführt worden.
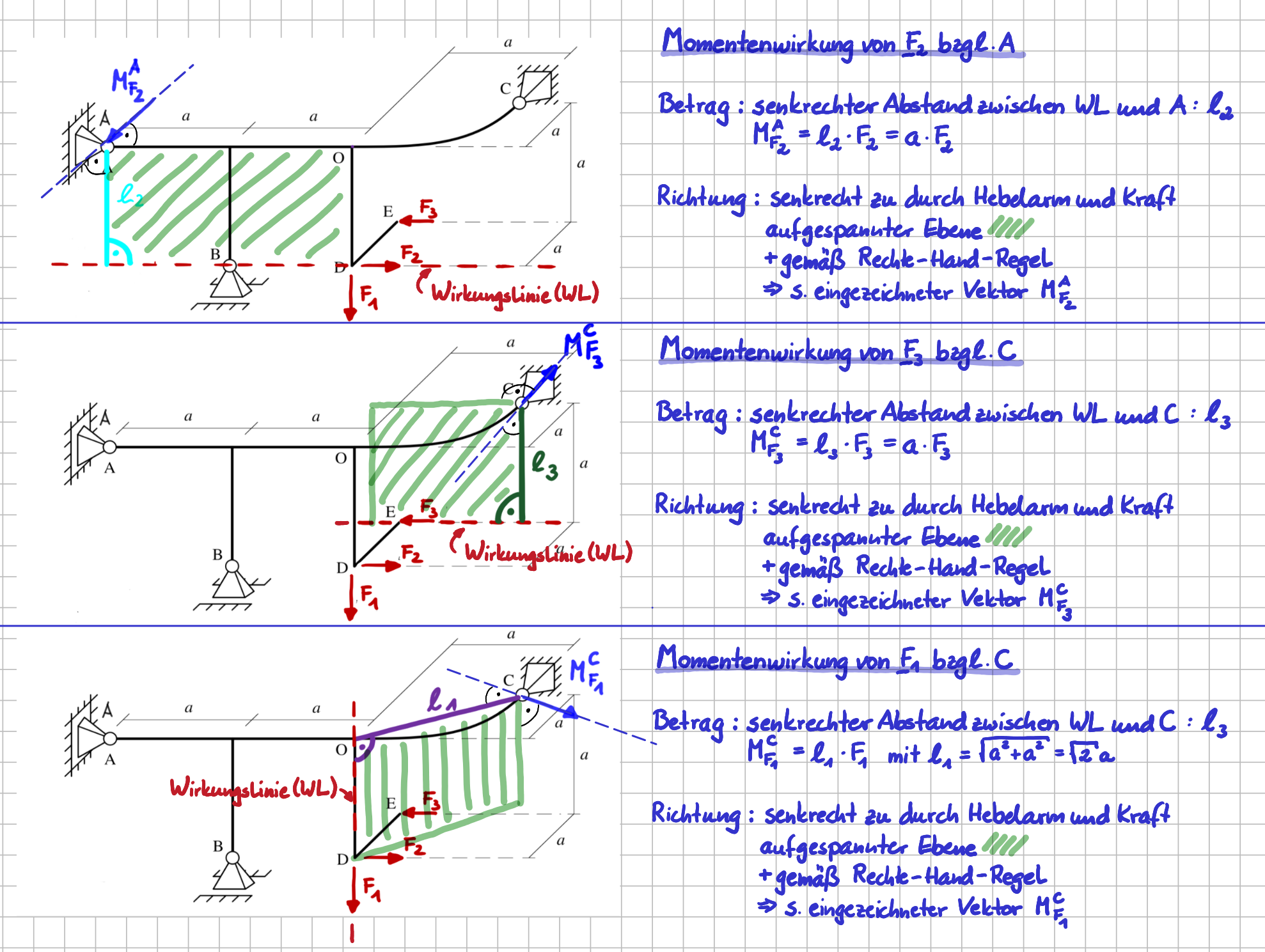
Momentenwirkung verschiedener Einzelkräfte für den räumlichen Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Momentenwirkung_verschiedener_Einzelkraefte_raumlicher_Fall.png
Wie du siehst, ist also im räumlichen Fall wirklich nichts anders, als im ebenen Fall. Sich in die Geometrie des Systems einzudenken ist natürlich aufwendiger. Aber auch hier gilt: Übung macht den Meister.
Zusammenfassung - Das Wichtigste in Kürze
Moment einer Einzelkraft
Ein Moment ist vom Typ "Vektor", hat also einen Betrag, eine Richtung und eine Wirkungslinie.
Eine Einzelkraft hat eine Momentenwirkung. Anders, als beim Kräftepaar, hängt diese Momentenwirkung von der Lage des Bezugspunktes relativ zur Wirkungslinie der Kraft ab.
Geht die Wirkungslinie der Kraft durch den Bezugspunkt, gibt es keine Momentenwirkung, d.h. das Moment ist Null.
Für den Betrag des Momentes gilt:
Der Betrag des Momentes einer Einzelkraft = (senkrechter Abstand zwischen der Wirkungslinie der Kraft und dem Bezugspunkt bzgl. dessen das Moment betrachtet wird) mal (Betrag der Kraft).
Die Kurzform hierfür ist: Moment = (Hebelarm) mal (Kraft).
Für die Richtung des Momentes gilt:
Der Momentenvektor steht immer senkrecht auf der Ebene, die durch die
Richtung der Kraft und die Richtung des Hebelarms aufgespannt wird.
Die Richtung des Momentes wird durch den 'Drehsinn' der Kraft relativ zum gewählten Bezugspunkt bestimmt.
Moment einer Einzelkraft - ebener Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Moment_einer_Einzelkraft_ebener_Fall.png
Moment einer Einzelkraft - räumlicher Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Moment_einer_Einzelkraft_raeumlicher_Fall.png
Der Momentenvektor steht immer senkrecht auf der Ebene, die durch die Richtung der Kraft und die Richtung des Hebelarms aufgespannt wird. In welche Richtung entlang der Normalen der Ebene der Momentenvektor zeigt, lässt sich mit der Rechte-Hand-Regel für Momente prüfen.
Schritt 1: Faust der rechten Hand in Momentenbezugspunkt legen
Schritt 2: Daumen in Richtung der Normalen der Ebene ausstrecken (hier gibt es zwei Möglichkeiten). Die Daumenrichtung ist identisch der Momentenrichtung, wenn die restlichen Finger in Richtung der betrachteten Kraft zeigen (und nicht entgegengesetzt).
Anwenden der Rechte-Hand-Regel für das Moment zur Bestimmung der Momentenrichtung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Rechte_Hand_Regel_Momentenrichtung%20%281%29.png
Die Richtung des Momentes der Kraft \( F_1 \) bezüglich des Punktes \( A \) ist senkrecht aus der Tischebene raus. Die Richtung des Momentes der Kraft \( F_2 \) bezüglich des Punktes \( A \) ist senkrecht in die Tischebene rein.
Arbeitsblatt - Teste dein Wissen
Test - Prüfe dein Wissen
3.2. ... mathematisch darstellen
Moment einer Einzelkraft
...mathematisch darstellen
Wenn es darum geht, das Moment einer Einzelkraft mathematisch darzustellen, also den Momentenvektor in Koordinaten anzugeben, hast du grundsätzlich zwei verschiedene Möglichkeiten:
- auf Basis des eben betrachteten mechanischen Verständnisses (Abschnitt 1)
- durch direktes Anwenden des Kreuzproduktes (Abschnitt 2)
Beide Wege führen selbstverständlich zu demselben Ergebnis.
Da dieses Kapitel recht lang ist, kannst du oben durch Klicken direkt zu Abschnitt 1 bzw. Abschnitt 2 springen.
Jeder Abschnitt hat seine eigene Zusammenfassung und seine eigenen Arbeitsmaterialien.
Mechanisches Verständnis mit an Board zu haben, ist immer vorteilhaft. Gleichzeitig gibt es natürlich auch Anwendungsfälle, in denen 'nur Rechnen' ausreichend oder hilfreich ist.
Bei ebenen Systemen ist der Ansatz über das Kreuzprodukt in der Regel "überkandidelt". Bei räumlichen Systemen kann es mit der mechanischen Verständnis über die Anschauung je nach Komplexität des Systems unübersichtlich werden. Und da die Berechnung mit Kreuzprodukt immer funktioniert, ist sie gerade bei diesen Systemen oft eine gute Wahl. Die Anschauung kann dann dazu dienen, berechnete Ergebnisse einem Plausibilitätscheck zu unterziehen.
Versuche also, beide Wege zu nutzen, damit du dann flexibel entscheiden kannst, welcher Weg in welcher Situation der für dich passender ist.
Wichtig ist: erst jetzt benötigst du ein Koordinatensystem. Alle Überlegungen zum mechanischen Verständnis haben wir komplett ohne Verwendung eines Koordinatensystems ausgeführt.
Abschnitt 1:
Auf Basis des mechanischen Verständnisses
das Moment einer Einzelkraft mathematisch darstellen
Mit dem mechanischen Verständnis aus dem vorangegangenen Abschnitt im Gepäck weißt du ja schon, in welche Richtung der Momentenvektor einer Einzelkraft bei einem gewählten Bezugspunkt zeigt und welchen Betrag er hat.
Wenn es jetzt also darum geht, den Vektor mathematisch zu beschreiben, musst du diese Informationen nur noch als Vektor bezüglich eines Koordinatensystems darstellen. Es ist also genau dasselbe Vorgehen, das du schon beim Moment eines Kräftepaars kennengelernt hast.
Machen wir es auch hier gleich konkret und greifbar und nehmen die beiden Beispiele aus der Zusammenfassung des vorherigen Kapitels. Dann kannst du das Vorgehen gleich einmal für den ebenen Fall und einmal für den räumlichen Fall anwenden.
Wir starten mit dem Beispiel des ebenen Systems und wählen als erstes ein Koordinatensystem ... genauer gesagt zwei: dann kannst du gleich selbst ausprobieren, was es genau bedeutet, dass die Darstellung des Vektors unterschiedlich ist, je nach gewähltem Koordinatensystem.
Grundsätzlich kannst du dir Koordinatensysteme wählen, so wie "du lustig bist". An der Mechanik ändert sich dadurch rein gar nichts. Einzig und allein die mathematische Darstellung kann, \(-\) je nach gewähltem Koordinatensystem \(-\) einfacher oder schwieriger sein.
Betrachten wir noch einmal die Momentenwirkung der Kraft \( \vec{F}_1 \).
Du siehst, dass ich zwei Koordinatensysteme gewählt habe:
das magenta-farbene und das orange.
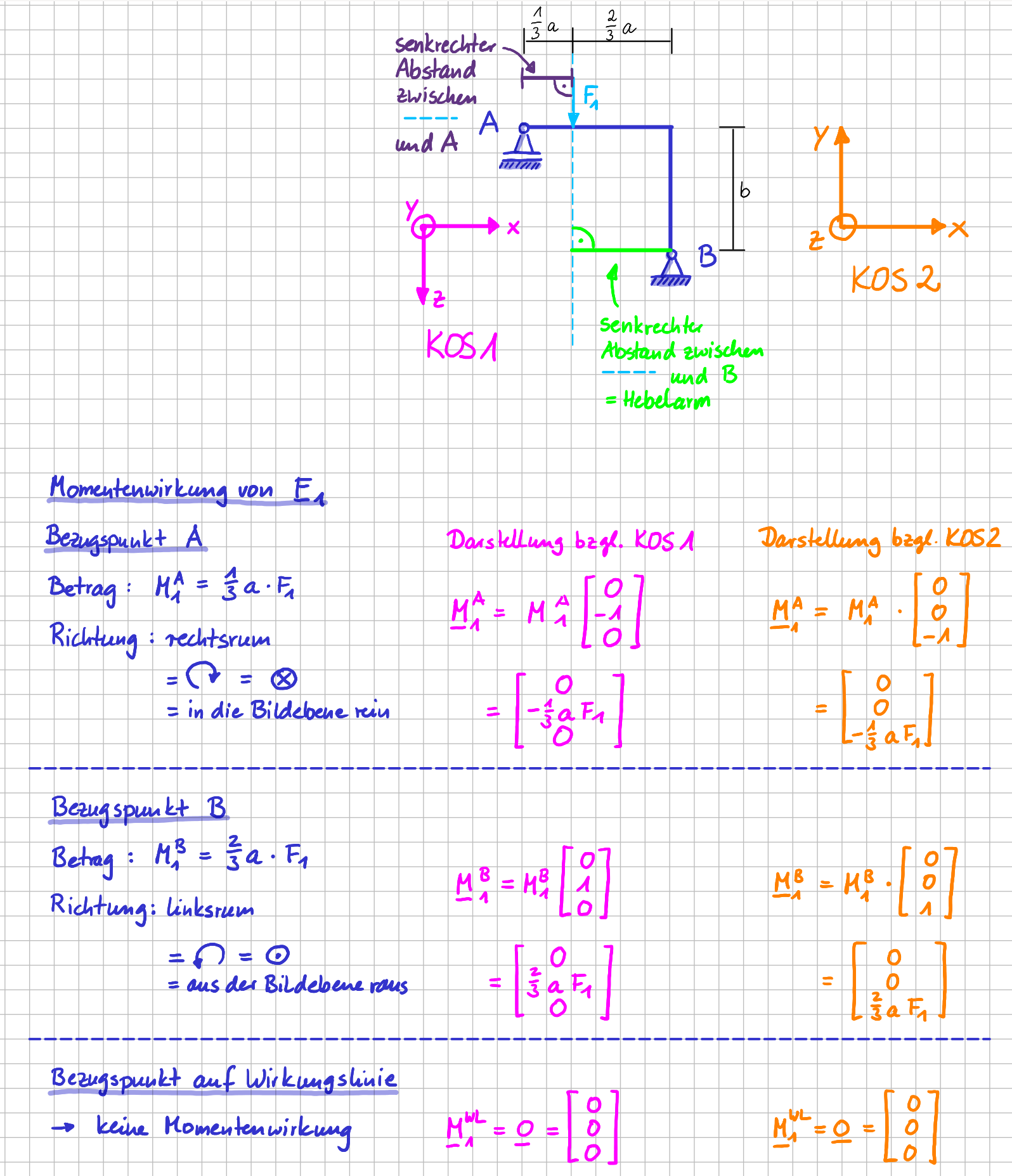
Mathematische Darstellung der Momentenvektoren der Kraft \(\vec{F}_1\) bezüglich zwei verschiedener Koordinatensysteme
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Mathematische_Darstellung_Momentenvektor_verschiedene_KOS.png
Betrag und Richtung der Momentenvektoren bezüglich der drei verschiedenen Punkte (\( A \), \( B \), Punkt auf Wirkungslinie) sind ja schon klar. Das haben wir uns ja eben im Kapitel "mechanisch verstehen" bereits überlegt.
Hier geht es jetzt also 'nur' noch darum, diese Vektoren bezüglich der beiden Koordinatensysteme darzustellen. Da es sich um ein ebenes System handelt, zeigen die Momentenvektoren alle in Richtung der Achse senkrecht zur Bildebene, was im Fall des magenta-farbenen KOS die \( y \)-Achse ist. Das Vorzeichen der \( y \)-Komponente ist für den Momentenvektor mit \( A \) als Bezugspunkt negativ, da der Momentenvektor "in den Bildschirm hinein", also in Richtung der negativen \( y \)-Achse zeigt.
Für \( B \) als Bezugspunkt ist es genau umgekehrt, weshalb der Eintrag in der \( y \)-Komponente ein positives Vorzeichen hat.
Bei einem Punkt auf der Wirkungslinie als Bezugspunkt für das Moment der Kraft \( \vec{F}_1 \) ist der Momentenvektor ohnehin der Nullvektor.
Nach der gleichen Vorgehensweise kannst du dir auch die Darstellung der Momentenvektoren bezüglich des orangen Koordinatensystems überlegen.
Mit dem mechanischen Verständnis im Gepäck war dieser Schritt doch jetzt ganz einfach, oder? Wenn du das anders siehst, da du dich mit Vektoren noch nicht so gut auskennst, dann arbeite doch gerne an dieser Stelle erstmal die Lektion "Vektorrechnung" durch.
An dieser Stelle lohnt es sich, noch einen anderen Anwendungsfall für die Rechte-Hand-Regel für Momente kennenzulernen.
Stell dir vor, du hast ein mechanisches System gegeben, bleiben wir wegen der Einfachheit des Zeichnens bei einem ebenen System. Das Koordinatensystem ist so vorgegeben, dass die \( x -\)Achse nach rechts und die \( z- \)Achse nach unten zeigt. Dann ist klar, dass die Momentenwirkung, die aus der Kraft \( \vec{F} \) resultiert, in Richtung der \( y -\)Achse zeigt.
Mit der Rechte-Hand-Regel kannst du jetzt schnell prüfen, ob es sich um ein positives Moment bezüglich der \( y- \)Achse handelt.
Fangen wir mit \( C \) als Bezugspunkt an:
Schritt 1: Leg deine rechte Hand als Faust in Punkt \( C \).
Schritt 2: Streck den Daumen in Richtung der \( y -\)Achse aus.
Schritt 3: Prüfe, ob der 'Drehsinn' der Kraft \( \vec{F} \) in Richtung oder entgegen der Richtung der restlichen Finger ist. Ist der 'Drehsinn' in Richtung der restlichen Finger, handelt es sich um ein positives Moment in Richtung der \( y- \)Achse. Du kannst auch "Es handelt sich um ein positives Moment um die \( y- \)Achse." sagen.
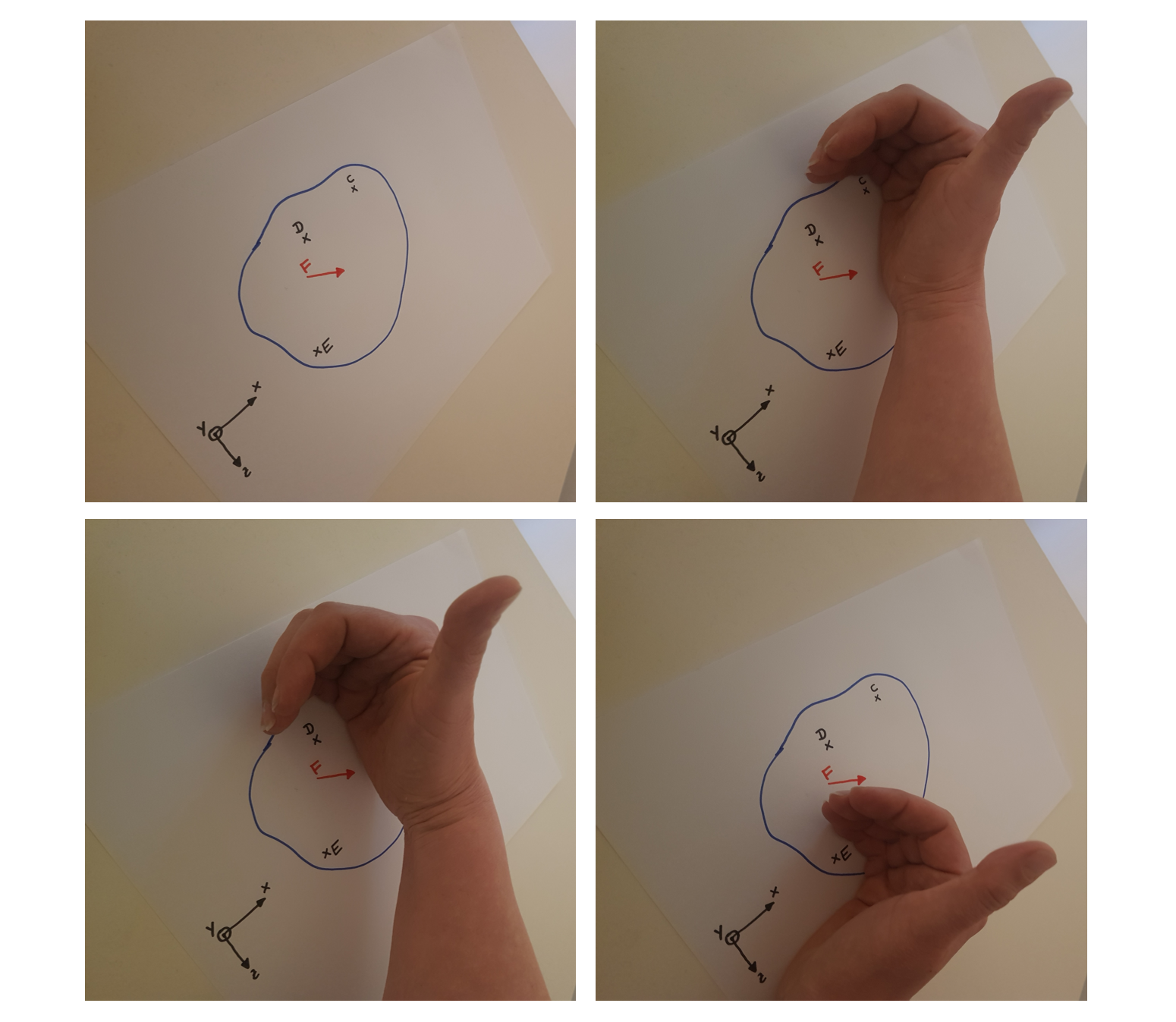
Überprüfen des Vorzeichens eines Momentes in Abhängigkeit vom Bezugspunkt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Ueberpruefen_Vorzeichen_Moment_Einzelkraft_Bezugspunkt%20%281%29.png
Das Moment der Kraft \( \vec{F} \) bezüglich Punkt \( C \) ist also positiv. Dasselbe gilt für Punkt \( D \) als Bezugspunkt. Bei Punkt \( E \) ist es anders: der Drehsinn ist entgegen der restlichen Finger und damit ist das Moment negativ.
Zusammenfassung - Das Wichtigste in Kürze
Mit der Rechte-Hand-Regel für Momente kannst du prüfen, ob die Momentenwirkung einer Einzelkraft bzgl. einer Koordinatenachse positiv oder negativ ist.
Vorgehen:
Schritt 1:
Leg deine rechte Hand als Faust in den Bezugspunkt.
Schritt 2:
Streck den Daumen in die positive Richtung derjenigen Achse aus, um die das Moment wirkt.
Schritt 3:
Prüfe, ob der 'Drehsinn' der Kraft in Richtung oder entgegen der Richtung der restlichen Finger ist. Ist der 'Drehsinn' in Richtung der restlichen Finger, handelt es sich um ein positives Moment. Du kannst auch "Es handelt sich um ein positives Moment um diese Achse." sagen.
Die Wirkungslinie der Kraft \(\vec{F}\) und die Punkte \(C\) , \(D\) und \(E\) liegen in der \(xz-\)Ebene. Damit ist klar, dass die Momentenwirkung der Kraft \(\vec{F}\) in Richtung der \(y-\)Achse zeigt.
Mit der Rechte-Hand-Regel ergeben sich folgende Vorzeichen:
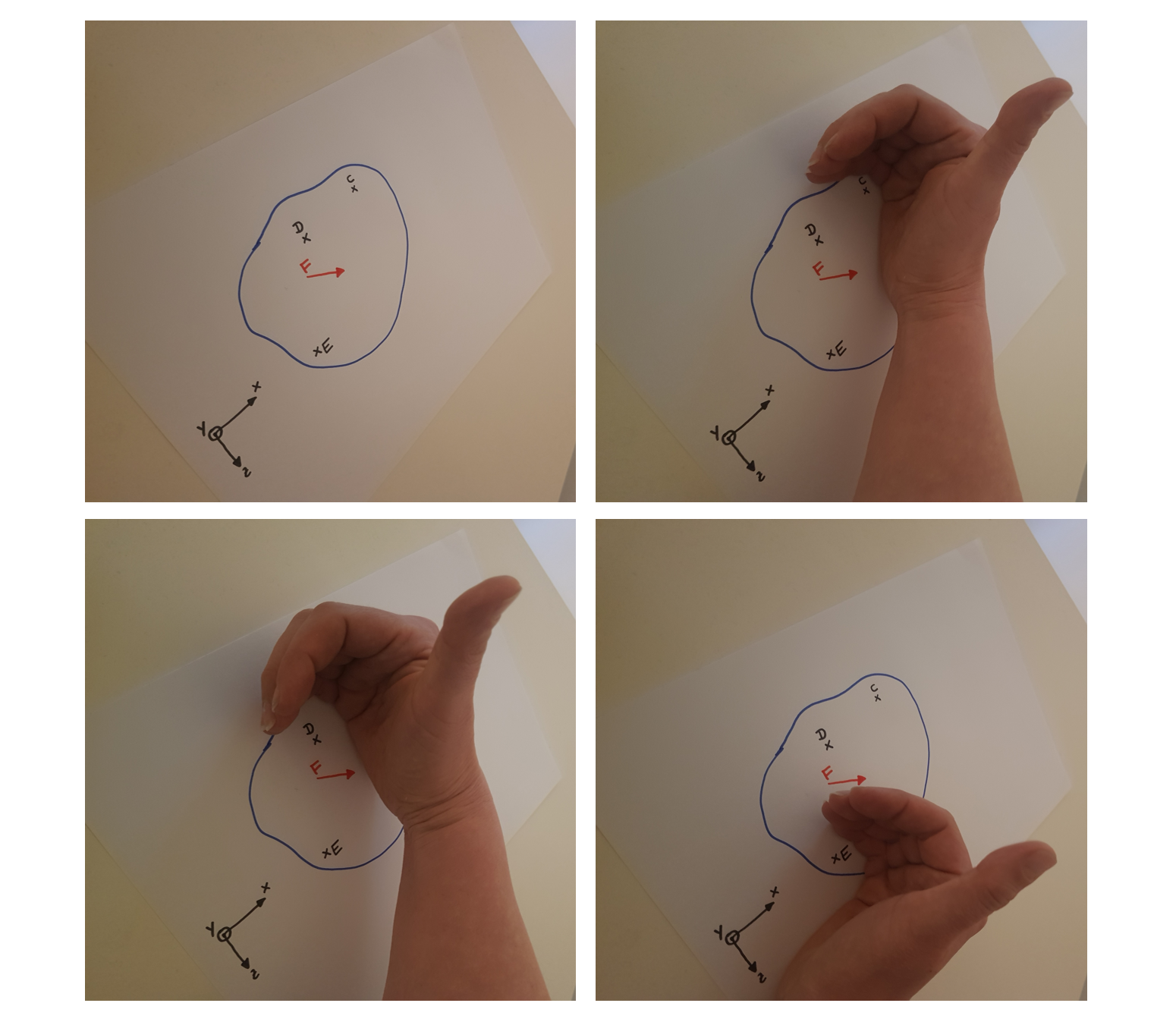
Beispiel: Rechte-Hand-Regel für Momentenwirkung einer Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Ueberpruefen_Vorzeichen_Moment_Einzelkraft_Bezugspunkt.png
Arbeitsblatt - Teste dein Wissen
Abschnitt 2:
Auf Basis des Kreuzproduktes
das Moment einer Einzelkraft mathematisch darstellen
Die Momentenwirkung einer Einzelkraft bezüglich eines bestimmten Bezugspunktes kannst du immer auch direkt über das Kreuzprodukt berechnen. Gerade in dreidimensionalen Systemen ist dies oft der schnellste Weg. Die Berechnungsvorschrift lautet:

Ebenes System für den Einstieg in die Berechnung des Momentes mit dem Kreuzprodukt: Teil 1
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Ebenes_System_Moment_Kreuzprodukt_Teil1.png
Wenn du dich daran erinnerst, wie du vorgehen würdest, wenn du auf Basis des mechanischen Verständisses argumentierst, würdest du dir als erstes überlegen, dass das Moment um die \( z \)-Achse wirkt. Mit der Rechte-Hand-Regel für Moment würdest du feststellen, dass das Moment positiv ist. Und der senkrechte Abstand zwischen Punkt und Wirkungslinie ist die Länge \( \ell_2 \). Du könntest also nur mit dem mechanischen Verständnis den Vektor hinschreiben:
$$\vec{M}^A = \begin{pmatrix} 0 \\ 0 \\ \ell_2 \cdot F_H \end{pmatrix}.$$
Mal schauen, ob wir mit dem Kreuzprodukt wirklich auf dasselbe Ergebnis kommen.
Der Vektor \( \vec{r} \) kann wie gesagt ein Vektor vom Bezugspunkt zu einem beliebigen Punkt auf der Wirkungslinie sein. Nehmen wir doch einfach den, der von \( A \) senkrecht nach oben zeigt, das sei \( \vec{r}_{\mathrm{senkrecht}}\) und den, der von \( A \) zum Angriffspunkt der Kraft zeigt, das sei \( \vec{r}_{\mathrm{Angriffspunkt}} \). Dann gilt für die Ortsvektoren und das Kreuzprodukt mit der Kraft \( \vec{F}\):
$$
\vec{r}_{\mathrm{senkrecht}}=\begin{pmatrix} 0 \\ \ell_2 \\ 0 \end{pmatrix} \qquad\vec{r}_{\mathrm{Angriffspunkt }}=\begin{pmatrix} \ell_1 \\ \ell_2 \\ 0 \end{pmatrix} \qquad \vec{F_H}=\begin{pmatrix} -F_H \\ 0 \\ 0 \end{pmatrix}
$$
$$
\rightarrow \vec{M}^A = \vec{r}_{\mathrm{senkrecht}} \times \vec{F_H}=\begin{pmatrix} 0 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F_H \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\\ell_2 \cdot F_H \end{pmatrix}
$$
$$
\rightarrow \vec{M}^A = \vec{r}_{\mathrm{Angriffspunkt}} \times \vec{F_H}=\begin{pmatrix} \ell_1 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F_H \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\\ell_2 \cdot F_H \end{pmatrix}
$$
Es ist also in der Tat egal, welchen Vektor vom Bezugspunkt zur Wirkungslinie du verwendet: Es kommt derselbe Momentenvektor heraus.
Was kannst du daraus schlussfolgern:
Das, was du beim Bestimmen des Momentes über das mechanische Verständnis in Einzelschritten machst (1. Überlegen, in welche Richtung das Moment zeigt, 2. Hebelarm, also senkrechten Abstand bestimmen, um Betrag der entsprechenden Momentenkomponente zu berechnen) macht das Kreuzprodukt also 'alles in Einem' und ganz automatisch.
Das bedeutet selbstverständlich nicht(!), dass du ab sofort alle Momentenwirkungen von Einzelkräften mit dem Kreuzprodukt berechnen solltest. Ganz im Gegenteil. Wo immer es geht, nutze das mechanische Verständnis als Basis. Und selbst bei räumlichen Systemen, bei denen du vermutlich meistens das Kreuzprodukt nutzen wirst, kannst du deine Ergebnisse immer noch mit deinem mechanischen Verständnis kontrollieren.
Lass uns das System von eben noch ein bisschen erweitern und eine vertikale Kraftkomponente dazunehmen.

Ebenes System für den Einstieg in die Berechnung des Momentes mit dem Kreuzprodukt: Teil 2
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Ebenes_System_Moment_Kreuzprodukt_Teil2.png
$$\vec{M}^A = \begin{pmatrix} 0 \\ 0 \\ \ell_2 \cdot F_H - \ell_1 \cdot F_V \end{pmatrix}.$$
Über das Kreuzprodukt, wenn du den Angriffspunkt für die Bestimmung des Ortsvektors nimmst, sieht das Ganze so aus
$$
\vec{M}^A = \vec{r}_{\mathrm{Angriffspunkt}} \times (\vec{F}_H+\vec{F}_V)=\begin{pmatrix} \ell_1 \\ \ell_2 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F_H \\ -F_V \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\\ell_2 \cdot F_H - \ell_1 \cdot F_V\end{pmatrix}.
$$
Es kommt selbstverständlich wieder auf beiden Wegen dasselbe heraus. Und vielleicht wirst du mir zustimmen, dass es schneller ist, über das mechanische Verständnis auf den Momentenvektor zu kommen, als über das Kreuzprodukt.
Exkurs zum weiteren Nachdenken
Für alle, die noch ein bisschen mechanisch denken und ausprobieren mögen: Lass uns mit diesem Beispiel noch einen Schritt weiter gehen. Du könntest die Kräfte \( \vec{F}_H \) und \( \vec{F}_V \) ja auch als Komponenten der Kraft \( \vec{F}_{Res} \) sehen.

Ebenes System für den Ebenes System für den Einstieg in die Berechnung des Momentes mit dem Kreuzprodukt: Teil 3a
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Ebenes_System_Moment_Kreuzprodukt_Teil3a.png
Stell dir vor, dass das System von Anfang an wie im rechten Teil der vorherigen Abbildung dargestellt, gegeben wäre.

Ebenes System für den Ebenes System für den Einstieg in die Berechnung des Momentes mit dem Kreuzprodukt: Teil 3b
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Ebenes_System_Moment_Kreuzprodukt_Teil3b.png
Wenn du versucht hättest, über das mechanische Verständnis den Vektor, der die Momentenwirkung bezüglich des Punktes \( A \) beschreibt, aufzustellen, hättest du vermutlich erstmal "Hebelarm mal Kraft" gedacht und versucht den orange eingezeichneten Hebelarm zu bestimmen, oder? Dann hättest du gemerkt, dass das auf den ersten Blick vielleicht gar nicht so einfach ist und dich gefragt, ob das nicht auch einfacher geht. Klar hättest du die Kraft \( F_{Res} \) jetzt in ihre Komponenten zerlegen und dann mit den einzelnen beiden Hebelarmen der Kraftkomponenten rechnen können. Das ist dann wieder die Rechnung wie im vorangegangenen Schritt. Du hättest dich aber auch daran erinnern können, dass du für die Berechnung von Lagerreaktionen Kräfte ja entlang ihrer Wirkungslinie verschieben kannst. Du könntest die Kraft \(F_{Res}\) also in den Punkt \(B\) verschieben und dort in Komponenten zerlegen. Dann würdest du sofort sehen, dass es nur der vertikale Anteil der Kraft ist, der ein Moment mit dem Hebelarm \( \frac{3}{4}\ell_1 \) in negativer Richtung hat, also $$ \vec{M}^A = \begin{pmatrix} 0 \\ 0 \\ - \frac{3}{4} \ell_1 \cdot F_V \end{pmatrix} $$ gilt. Wenn du von Anfang an mit dem Kreuzprodukt rechnen würdest, könntest du z.B. den Vektor von \( A \) nach \( B \) als Ortsvektor zu einem Punkt auf der Wirkungslinie der Kraft wählen. Dein Kreuzprodukt sähe dann also so aus: $$ \vec{M}^A = \vec{r}_{AB} \times \vec{F}_{Res}=\begin{pmatrix} \frac{3}{4}\ell_1 \\ 0 \\ 0 \end{pmatrix} \times \begin{pmatrix} -F_H \\ -F_V \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ - \frac{3}{4} \ell_1 \cdot F_V\end{pmatrix}. $$ Du siehst: es gibt also verschiedene Wege, um die Momentenwirktung einer Einzelkraft zu bestimmen. Wie immer gilt: Probiere an ein und derselben Aufgabe immer wieder mal verschiedene Wege aus. So kannst du deine ganz eigenen Erfahrungen sammeln, welchen Weg DU wann am sinnvollsten anwenden kannst.
Momentenwirkungen berechnest du ja zum Beispiel immer dann, wenn du Gleichgewichtsbedingungen für ein freigeschnittenes System aufstellst.
Lass uns beim folgenden System einfach mal schauen, wie die Momentenwirkung der Kraft \( 2F \) bezüglich unterschiedlicher Bezugspunkte ist.
Bei der Wahl des Ortsvektors kannst du es dir möglichst einfach machen: du brauchst ja nur einen Vektor vom Bezugspunkt zu irgendeinem Punkt auf der Wirkungslinie der Kraft.
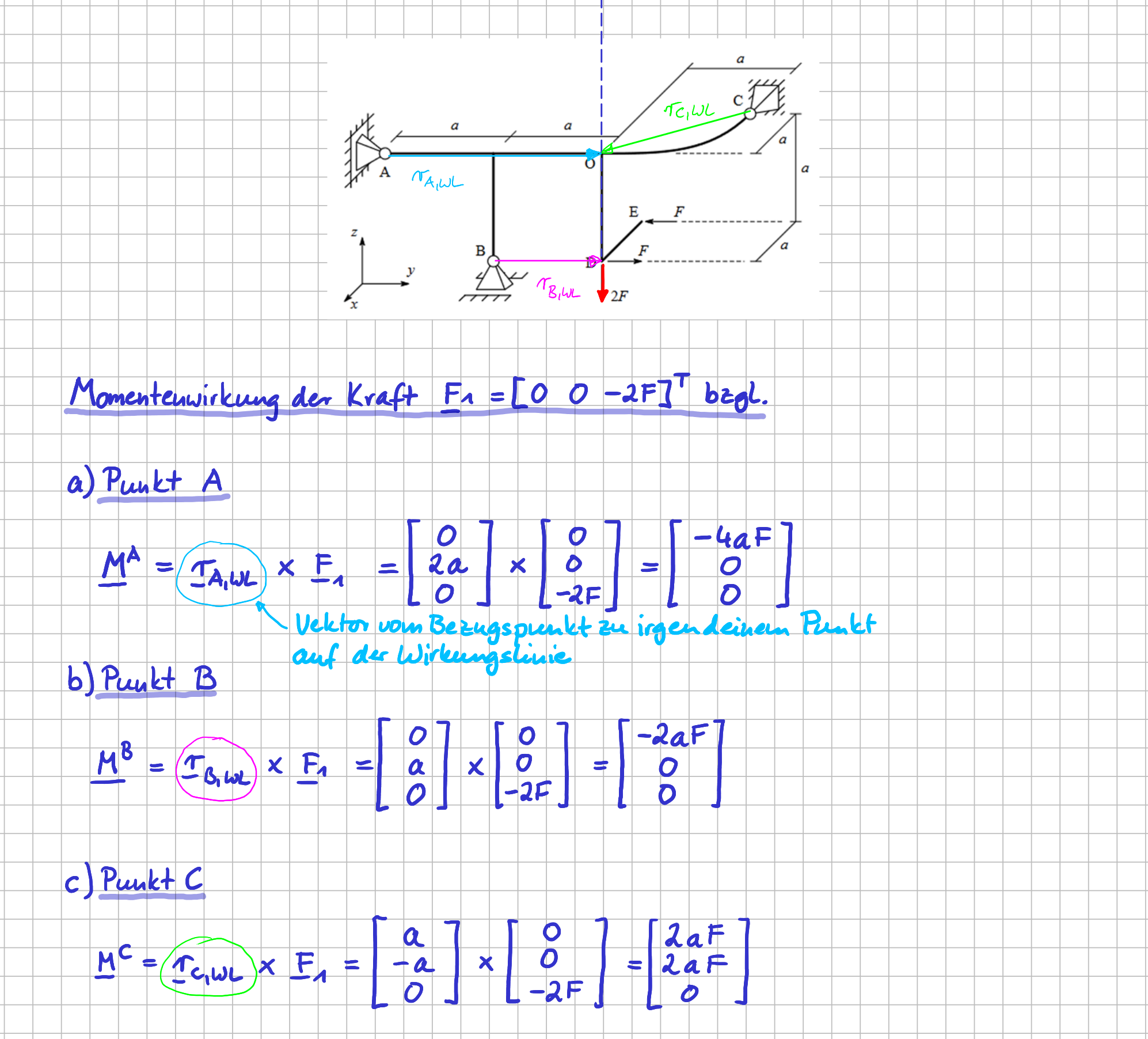
Berechnung des Momentenvektors einer Einzelkraft in einem räumlichen System: verschiedene Bezugspunkte
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Berechnung_Momentenvektor_Einzelkraft_raeumlich_Bezugspunkte.png
Ob du schneller im Bestimmen bist, wenn du über das mechanische Verständnis oder das Kreuzprodukt gehst, kannst du nur durch Ausprobieren herausfinden.
Zusammenfassung - Das Wichtigste in Kürze
Vektor vom Bezugspunkt zu einem beliebigen Punkt auf der Wirkungslinie der Kraft,
der Kraftvektor selber.
Denk dran, dass beim Kreuzprodukt die Reihenfolge, in der du die beiden Vektoren miteinander verrechnest, relevant ist.
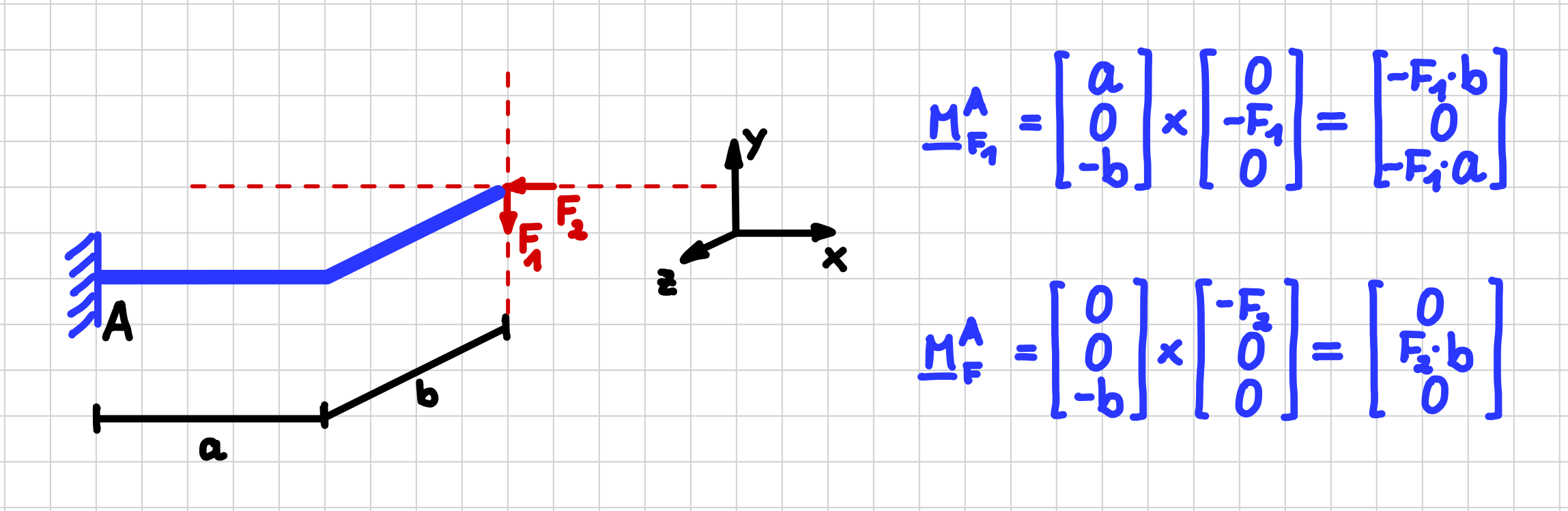
Bestimmung des Momentenvektors mittels Kreuzprodukt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2177/Rechte_Hand_Regel_Moment_Beispiel.png
Arbeitsblatt - Teste dein Wissen
4. Moment = freier Vektor
Momentenvektoren sind sogenannten freie Vektoren. Das bedeutet, dass die Momentenwirkung nach außen unabhängig davon ist, wo der Vektor am System angreift.
Dass das wirklich stimmt, zeige ich dir auch mit einem Experiment im folgenden Video.
5. Moment einer Einzelkraft mit Kräftepaar verstehen
Wenn du dich dem Moment einer Einzelkraft noch einmal aus einem anderen Blickwinkel nähern möchtest, dann kannst du einfach eine der zulässigen Operationen für Kräfte verwenden, nämlich dass Addieren des Nullvektors.
Nehmen wir einmal an, dass dich in dem folgenden System die Momentenwirkung der Einzelkraft \(2F\) bezüglich des Punktes \(A\) interessiert ... z.B. weil du diesen Anteil brauchst, um das Momentengleichgewicht bezüglich des Punktes \(A\) aufzustellen.
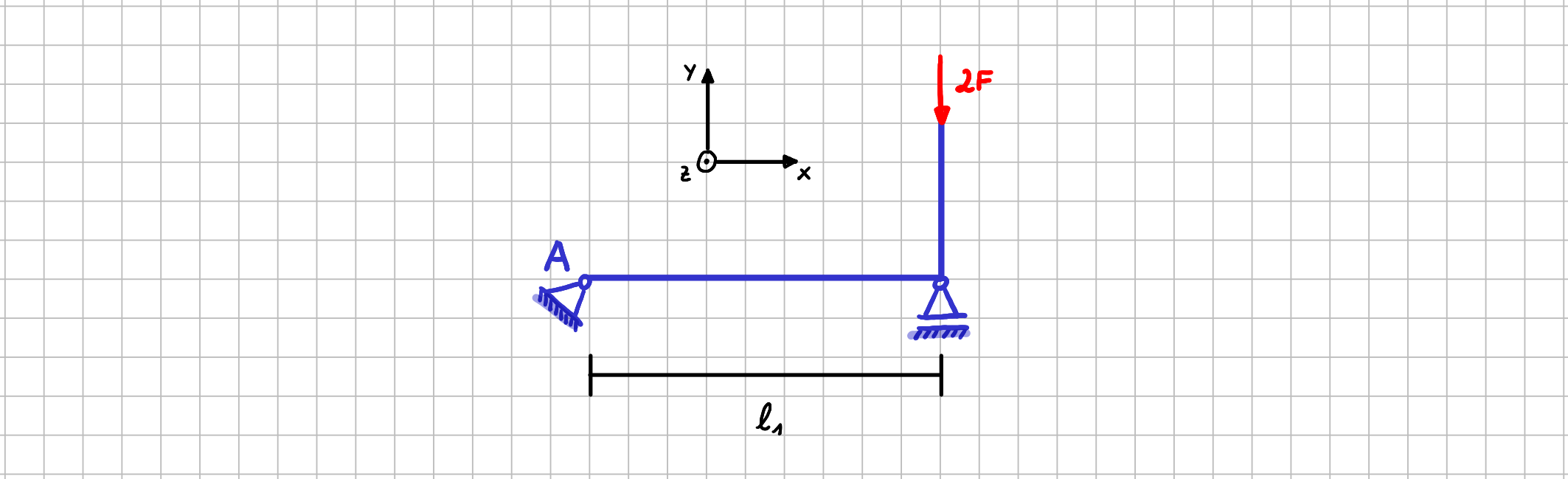
System für die Betrachtung der Momentenwirkung einer Einzelkraft mit Hilfe des Kräftepaars
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2182/System_Zusammenhang_Kraeftepaar_Momentenwirkung_Einzelkraft.png
Dann kannst du, so wie im Bild rechts dargestellt, im Punkt \(A\) einfach den Nullvektor in Form von zwei Kräften mit Betrag \(2F\) und entgegengesetzer Richtung ergänzen.
Wenn du jetzt die drei Kräfte "anders anschaust", dann siehst du, dass du eine Einzelkraft mit Betrag \(2F\) im Punkt \(A\) angreifen hast, die in dieselbe Richtung zeigt, wie die Kraft, deren Momentenwirkung du berechnen willst. Zusätzlich hast du ein Kräftepaar.
Da die Wirkungslinien der beiden Kräfte den Abstand \( \ell_a \) haben, ist der Betrag des Momentes \(2F \cdot \ell_1 \) und die Richtung ist durch den Drehsinn der beiden Kräfte vorgegeben.
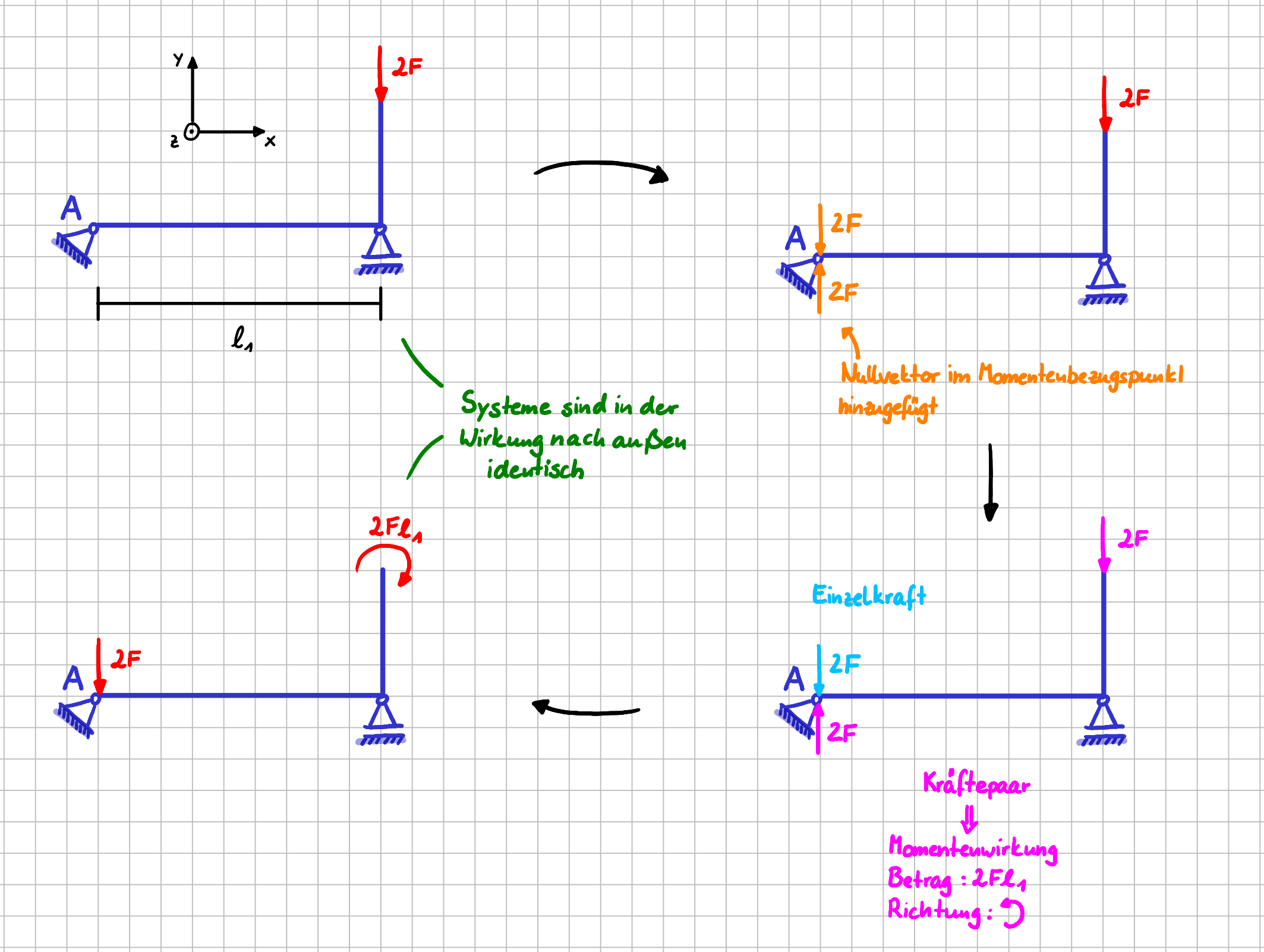
Momentenwirkung einer Einzelkraft erklärt mit Hilfe des Kräftepaars
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2182/Herleitung_Zusammenhang_Kraeftepaar_Momentenwirkung_Einzelkraft.png.png?time=1735557798481
Das Ausgangsssystem und das System, bei dem die Kraft \(2F\) im Punkt \(A\) angreift und das Einzelmoment \(2F\ell_1\) angreift, sind also in der Wirkung nach außen identisch.
Wo du das Moment einzeichnest, ist dabei vollkommen egal, da das Moment ein freier Vektor ist.
Durch das Einführen des Nullvektors ist mit der Ausgangskraft also ein Kräftepaar entstanden, aus dem die Momentenwirkung der Ausgangskraft "direkt" sichtbar gemacht werden kann.

