Moment
Moment
3. Moment einer Einzelkraft
3.1. ... mechanisch verstehen
Moment einer Einzelkraft
... mechanisch verstehen
Bestimmt hast du schon mal "Moment ist gleich Hebelarm mal Kraft" gehört. Diese Aussage ist genau dann richtig, wenn 'Hebelarm' als Kurzform von "senkrechter also kürzester Abstand zwischen der Wirkungslinie der Kraft und Bezugspunkt bzgl. dessen das Moment bestimmt wird" verstanden wird, 'Moment' als Kurzform für "Betrag des Momentes" und 'Kraft' als Kurzform von "Betrag der Kraft".
Damit das ganze übersichtlich wird, findest du hier Kurz- und Langform nebeneinander:

Bestimmung des Betrags des Momentes einer Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Bestimmung_des_Betrags_des_Moments_einer_Einzelkraft.png
Klingt kompliziert?
Wenn nein, umso besser.
Wenn ja, dann immer mit der Ruhe. Wir schauen uns das Schritt für Schritt an.
In jedem Fall haben wir schon mal eine sehr präzise Aussage für die Bestimmung des Betrags des Moments. Die gilt es jetzt zu verstehen. Und dann brauchen wir auch noch eine Aussage dazu, wie man die Richtung des Momentes einer Einzelkraft bestimmt.
Also ... irgendwie scheint schon mal klar zu sein, dass die Momentenwirkung einer Einzelkraft davon abhängt, bezüglich welchen Punktes man schaut.
Stellt sich die Frage: hat eine Einzelkraft überhaupt immer eine Momentenwirkung?
Es kommt darauf an......
In der nächsten Abbildung ist ein System bestehend aus einem Winkel und einem Los- und einem Festlager gezeigt. An ihm greifen die Kräfte \( \vec{F}_1\) und \(\vec{F}_2 \) wie dargestellt an. In der Darstellung rechts sind zusätzlich noch die Wirkungslinien der beiden Kräfte eingezeichnet.
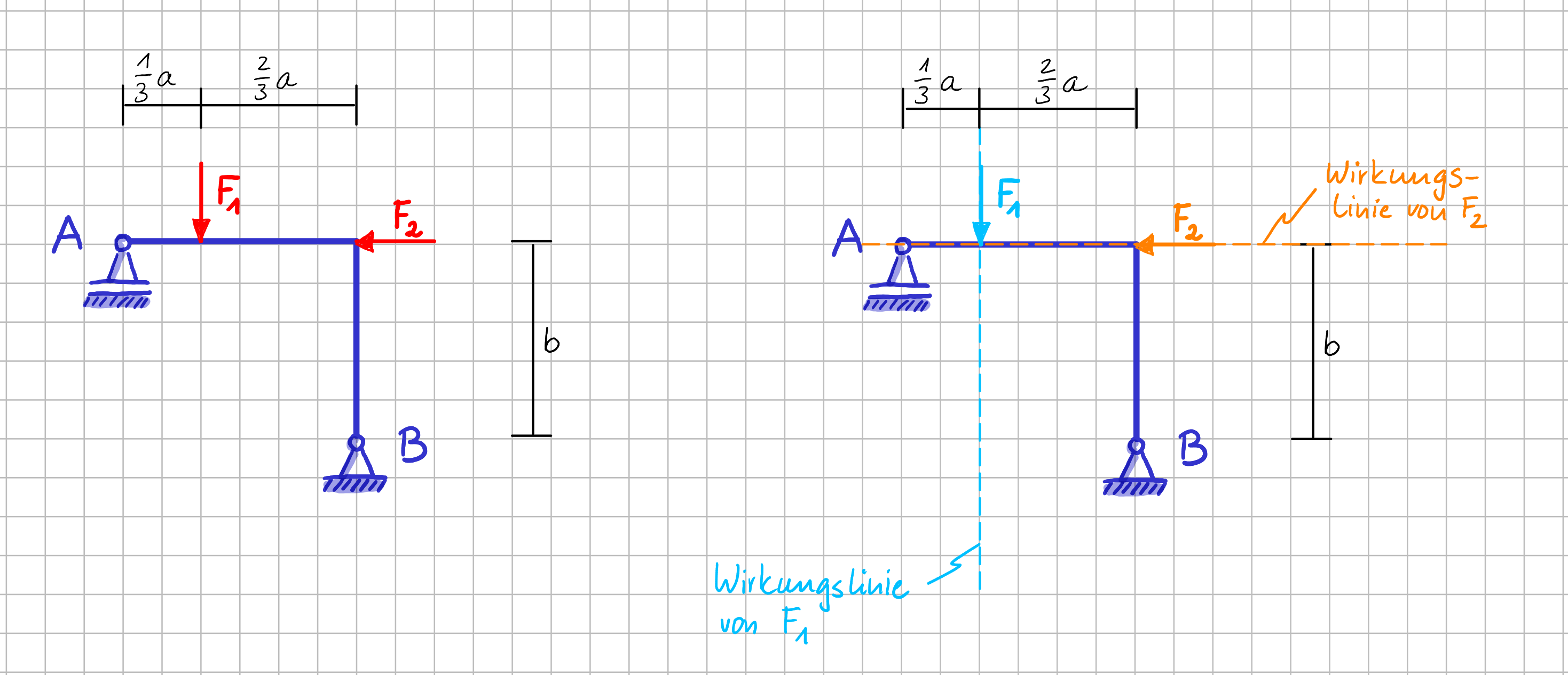
Ebenes System zur Veranschaulichung der Momentenwirkung einer Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Ebenes_System_Moment_Einzelkraft.png
Dir fällt bestimmt auf, dass kein Koordinatensystem gegeben ist. Das brauchen wir in diesem Abschnitt ja auch gar nicht, da wir erstmal auf der mechanischen Ebene verstehen wollen, was los ist.
Fangen wir mit der Kraft \( \vec{F}_2 \) an.
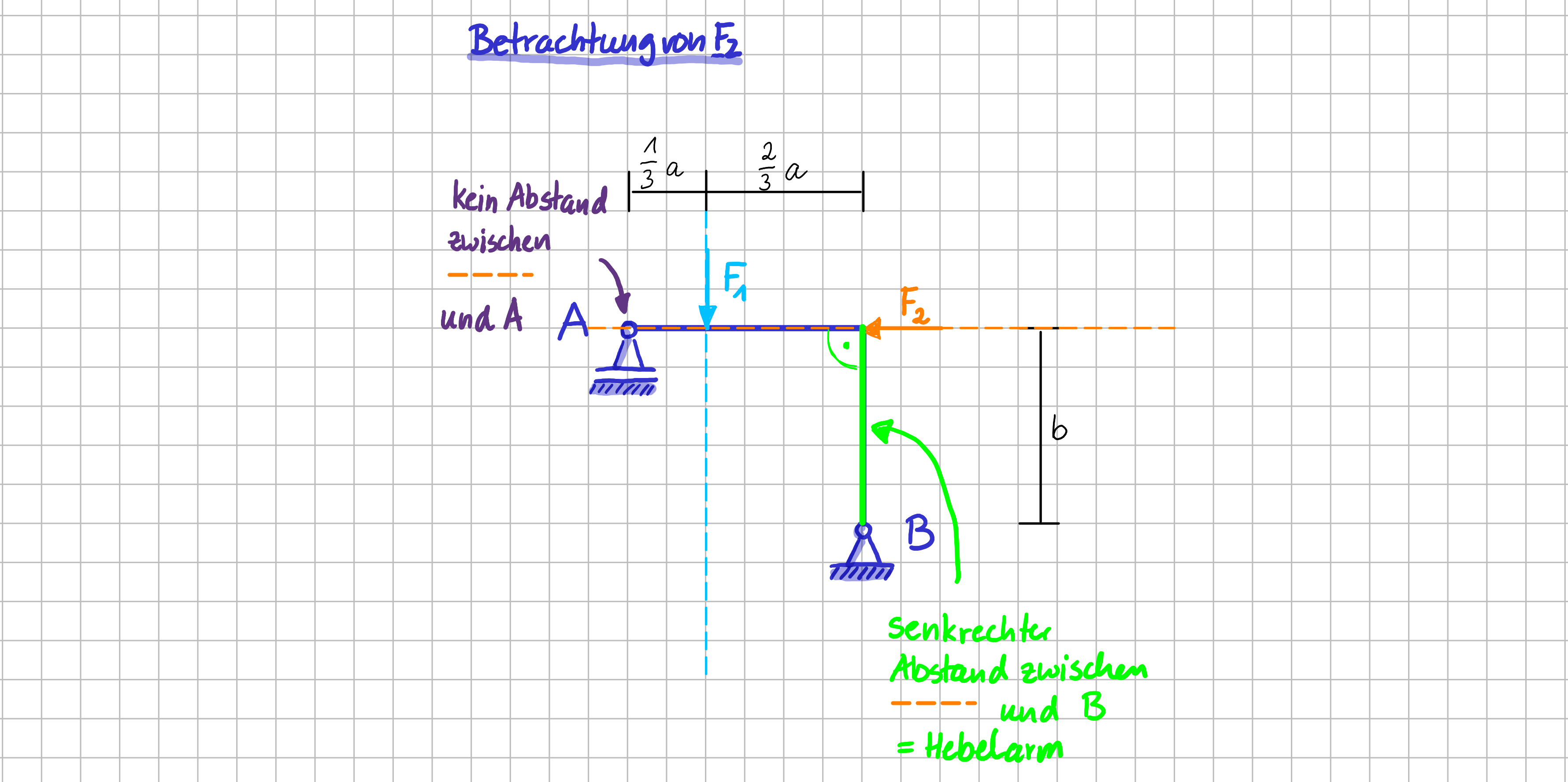
Betrachtung der Momentenwirkung der beiden Kräfte im Detail: \(\vec{F}_2\)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Betrachtung_Momentenwirkung_im_Detail.png
Die Momentenwirkung einer Kraft hängt von der Wahl des Bezugspunktes ab. Die Wirkungslinie der Kraft \( F_2 \) geht zum Beispiel durch den Punkt \( A \). Wenn wir also fragen "Hat die Kraft \( F_2 \) bzgl. des Punktes \( A \) einen Momentenwirkung?", so lautet die Antwort 'Nein'. Der Hebelarm, also der senkrechte Abstand zwischen Wirkungslinie der Kraft und Bezugspunkt, ist Null: Wie soll da ein Abstand sein, wenn die Wirkungslinie durch den Punkt geht?
Fragen wir "Hat die Kraft \( \vec{F}_2 \) bzgl. des Punktes \( B \) einen Momentenwirkung?", so lautet die Antwort 'Ja'. Mit diesem Bezugspunkt sieht die Welt anders aus: es gibt einen senkrechten Abstand zwischen Wirkungslinie der Kraft \( \vec{F}_2 \) und Bezugspunkt \( B \). Der Hebelarm ist die Strecke \(b\).
Für den Betrag des Momentes der Kraft \( \vec{F}_2 \) bezüglich Punkt \( B \) gilt also: \( M_2^B = b \cdot F_2 \)
Und wie sieht es mit der Richtung des Momentes aus? Die lässt sich ganz einfach bestimmen.
Stell dir vor, der Bezugspunkt \(B\) und die Wirkungslinie der Kraft \( F_2 \) sind wirklich physikalisch mit einem Balken verbunden. Dieser gedachte Balken ist im Bezugspunkt \(B\) drehbar gelagert. In welche Richtung würde die Kraft \( \vec{F}_2 \) den Balken um den Bezugspunkt \( B \) drehen wollen? Deine Antwort lautet 'linksrum', oder? Damit hast du schon die Richtung des Momentes gefunden.
Was jetzt kommt ist klar, oder? Wir schauen uns die Kraft \( \vec{F}_1 \) an.
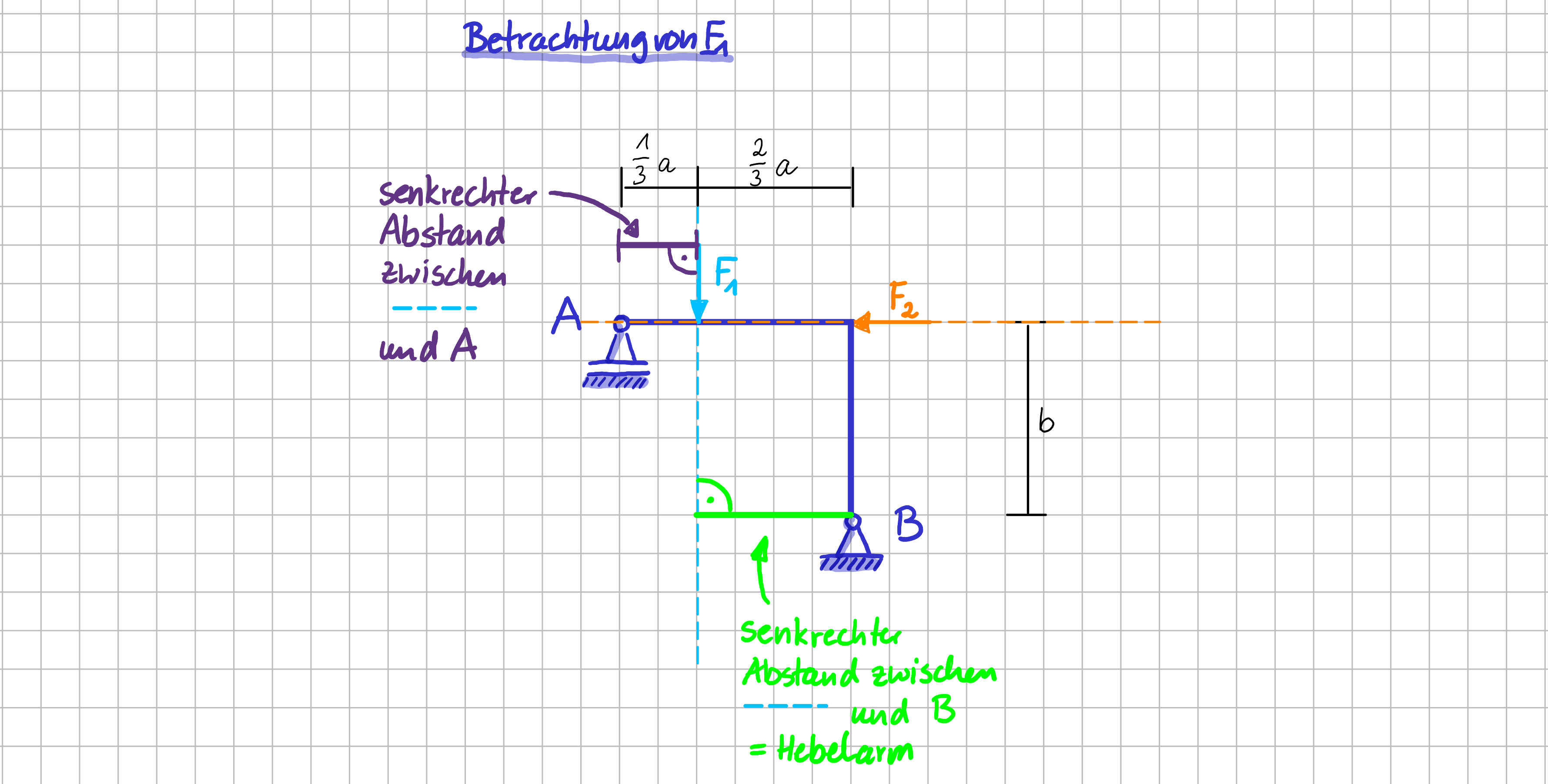
Betrachtung der Momentenwirkung der beiden Kräfte im Detail: \(\vec{F}_1\)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Betrachtung_Momentenwirkung_im_Detail_02.png
Bezüglich des Punktes \( A
\) hat die Kraft \( F_1 \) den senkrechten Abstand \( \frac{1}{3}a \). Der Betrag des Momentes der Kraft \( F_1 \) bzgl. des Punktes \( A \) ist also: \( M_1^A = \frac{1}{3}a \cdot F_1 \).
Und wie sieht es mit der Richtung des Momentes aus? Stell dir wieder vor, dass der Bezugspunkt, hier \( A \), mit einem Balken, der die Länge des Hebelarms hat, mit der Wirkungslinie der Kraft \( F_1 \) verbunden ist. In welche Richtung würde die Kraft diesen Balken drehen wollen? Jetzt lautet die Antwort 'rechtsrum'.
Und wie sieht es aus, wenn Punkt \( B \) als Bezugspunkt gewählt wird? Bezüglich des Punktes \( B \) hat die Kraft \( F_1 \) den senkrechten Abstand \( \frac{2}{3}a \). Der Betrag des Momentes der Kraft \( F_1 \) bzgl. des Punktes \( B \) ist also: \( M_1^A = \frac{2}{3}a \cdot F_1 \).
Und wie sieht es mit der Richtung des Momentes aus? Stell dir wieder vor, dass der Bezugspunkt, jetzt \( B \), mit einem Balken, der die Länge des Hebelarms hat, mit der Wirkungslinie der Kraft \( F_1 \) verbunden ist. In welche Richtung würde die Kraft diesen Balken drehen wollen? Jetzt lautet die Antwort 'linksrum'.
Für die Richtung des Momentes einer Einzelkraft können wir an dieser Stelle noch einige weitere Punkte ableiten:
Der Momentenvektor steht immer senkrecht auf der Ebene, die durch die Richtung der Kraft und die Richtung eines Verbindungsvektors zwischen Bezugspunkt und Wirkungslinie aufgespannt wird. In den betrachteten Beispielen ist diese Ebenennormale senkrecht zur Bildfläche. In welche Richtung entlang der Normalen der Ebene der Momentenvektor zeigt \(-\) raus aus der Ebene oder rein \(-\), lässt sich mit der Rechten-Hand-Regel für Momente prüfen.
Schritt 1: Faust der rechten Hand in Momentenbezugspunkt legen
Schritt 2: Daumen in Richtung der Normalen der Ebene ausstrecken (hier gibt es zwei Möglichkeiten).
Die Daumenrichtung ist identisch der Momentenrichtung, wenn die restlichen Finger in Richtung der betrachteten Kraft zeigen (und nicht entgegengesetzt).
Im folgenden Beispiel soll die Momentenwirkung der beiden Kräfte \( \vec{F}_1\) und \( \vec{F}_2 \) bezüglich des Bezugspunktes \( A \) betrachtet werden. Die rechte Hand befindet sich daher im Bezugspunkt \( A \). Es geht 'nur' darum, die Richtung rauszufinden.
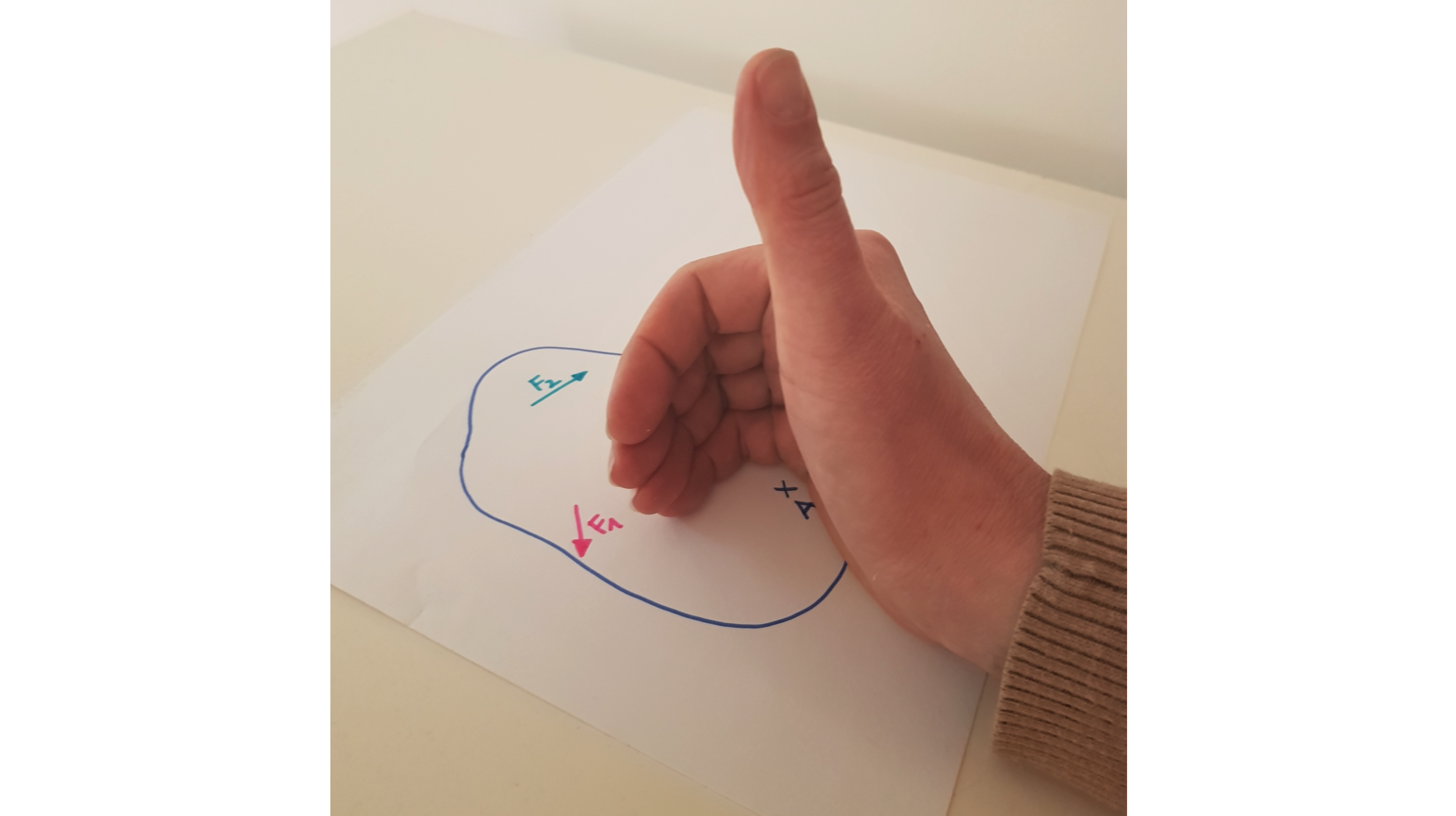
Anwenden der Rechte-Hand-Regel für das Moment zur Bestimmung der Momentenrichtung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Rechte_Hand_Regel_Momentenrichtung.png
Die beiden Kräfte liegen in der Tischebene. Es ist bereits klar, dass die Momente dieser Kräfte entweder senkrecht nach oben, oder senkrecht nach unten zeigen. Mit der Rechte-Hand-Regel kannst du schnell feststellen, dass das Moment der Kraft \( \vec{F}_1 \) senkrecht nach oben zeigt: Die Kraft \( \vec{F}_2 \) zeigt in Richtung der restlichen Finger, also ist die Momentenrichtung durch die Richtung des Daumens gegeben. Nach derselben Argumentation zeigt das Moment der Kraft \( \vec{F}_2 \) senkrecht nach unten.
Anhand der Betrachtung in diesem Abschnitt ist dir hoffentlich klargeworden, dass
- eine Einzelkraft eine Momentenwirkung haben kann,
- diese Momentenwirkung \( - \) in Bezug auf Richtung und Betrag\( - \) von der Wahl des Bezugspunktes abhängt und
- es eigentlich ganz einfach ist, Betrag und Richtung rauszufinden, wenn du wie oben beschrieben systematisch vorgehst.
Anhand des räumlichen Systems in der nächsten Abbildung ist geprüft worden, für welche Punkte \(A\), \(B\), \(C\), \(D\), \(O\) und \(H\) die drei Einzelkräfte keine Momentenwirkung haben. Das gilt natürlich für alle Punkte, die auf der Wirkungslinie der jeweiligen Kraft liegen. Von daher sind die beiden genannten Punkte jeweils nur zwei Beispiele.
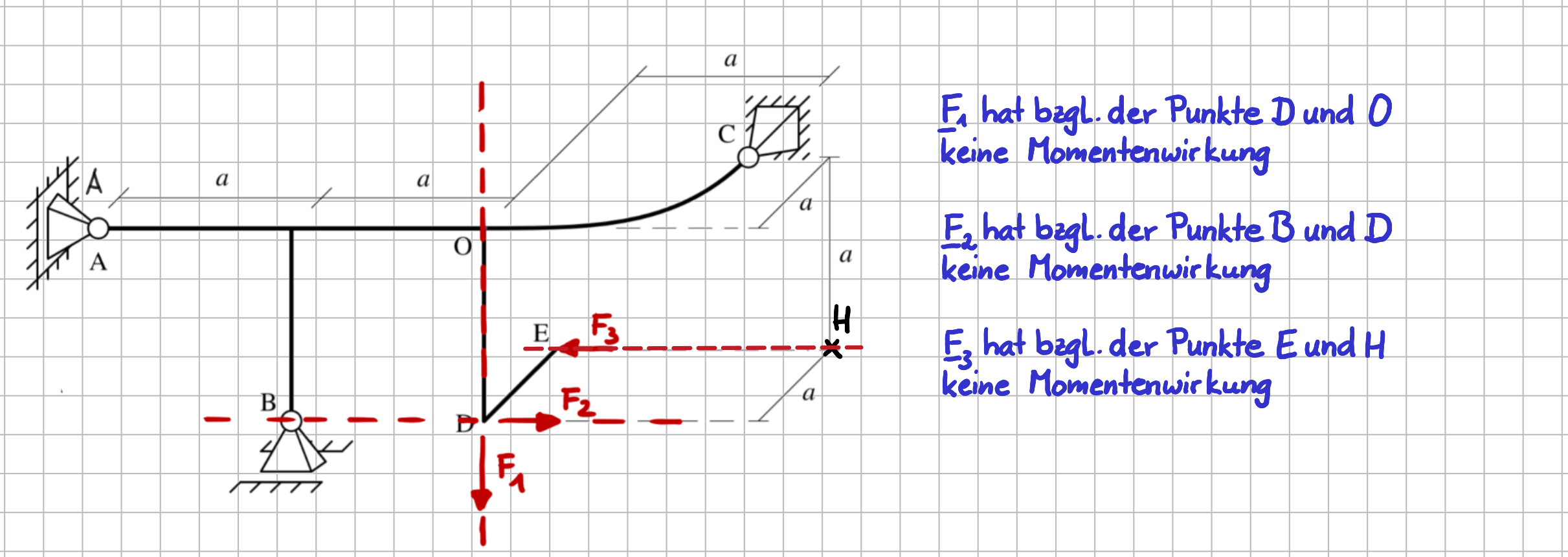
Verschwindende Momentenwirkung für den räumlichen Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/verschwindende_Momentenwirkung_raeumlicher_Fall.png
Exkurs zum Thema Gleichgewichtsbedingungen
Wichtig ist, dass du dir immer vergegenwärtigst, dass du beim Aufstellen des Momentengleichgewichts einen beliebigen Bezugspunkt wählen kannst. Es ist vom Grundsatz her vollkommen egal, welchen Bezugspunkt du nimmst. Wirklich. Es kann ein Punkt sein, der geometrisch auf einem Körper des Systems liegt. Es kann aber auch ein Punkt sein, der 'irgendwo in der Botanik' liegt, wie das z.B. beim Punkt \( H \) der Fall ist. Obwohl es theoretisch unendlich viele mögliche Bezugspunkte gibt, die du beim Aufstellen des Momentengleichgewichts wählen kannst, gibt es natürlich clevere und nicht so clevere Punkte. Clevere Punkte sind solche, durch die die Wirkungslinien möglichst vieler (unbekannter) Kräfte gehen. Bei der Wahl eines solchen Punktes reduziert sich die erforderliche Schreib- und Denkarbeit, da all diese Kräfte aufgrund des verschwindenden Hebelarms nicht ins Momentengleichgewicht eingehen.
Auch im räumlichen Fall lässt sich die Aufgabe, den Vektor der Momentenwirkung einer Einzelkraft bezüglich eine Bezugspunktes zu bestimmen, in zwei Teilschritte zerlegen:
- Bestimmung des Betrags und
- Bestimmung der Richtung des Momentenvektors.
In der folgenden Abbildung ist genau dieses Vorgehen für die drei Kräfte und je einen Bezugspunkt durchgeführt worden.
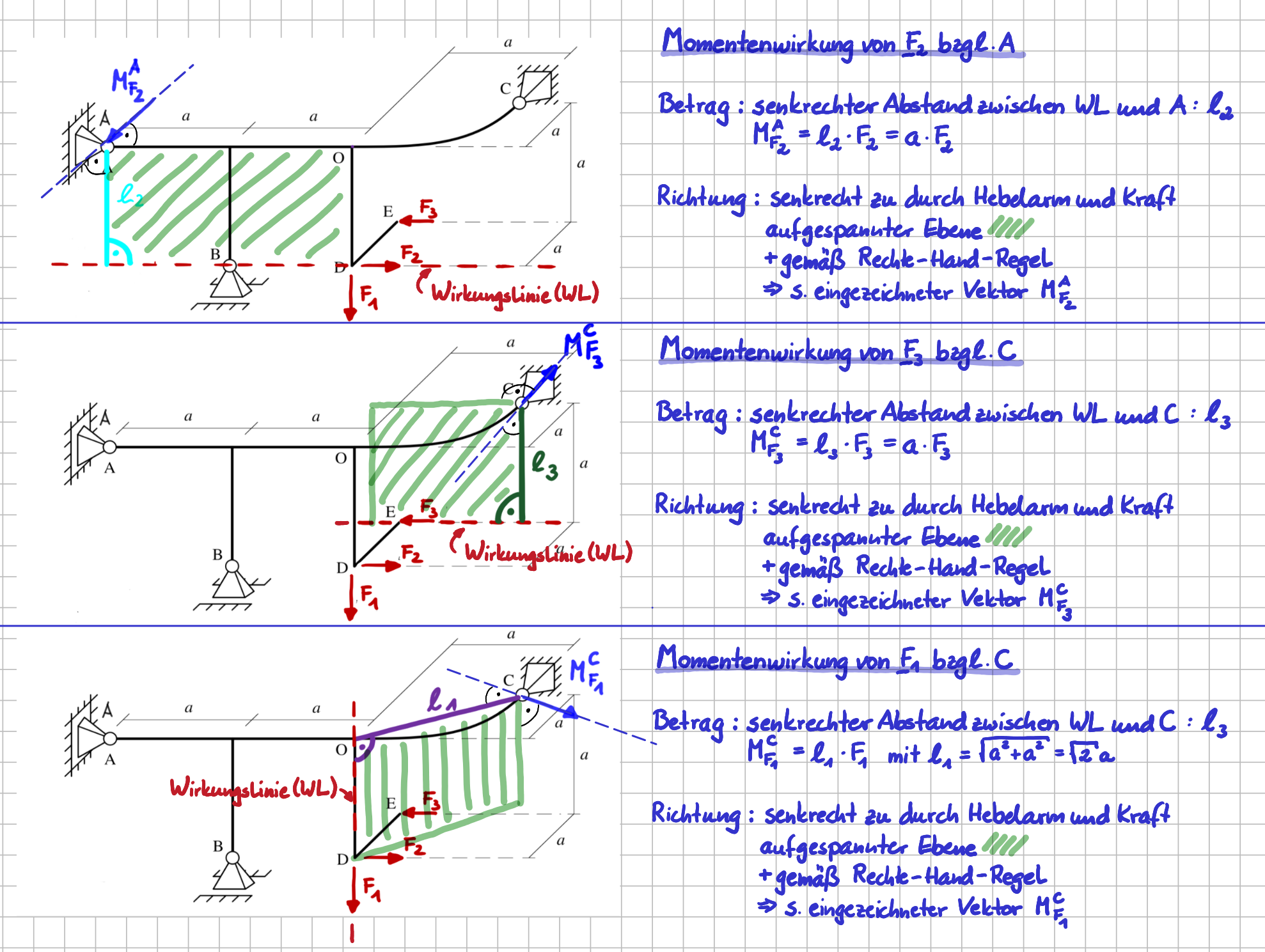
Momentenwirkung verschiedener Einzelkräfte für den räumlichen Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Momentenwirkung_verschiedener_Einzelkraefte_raumlicher_Fall.png
Wie du siehst, ist also im räumlichen Fall wirklich nichts anders, als im ebenen Fall. Sich in die Geometrie des Systems einzudenken ist natürlich aufwendiger. Aber auch hier gilt: Übung macht den Meister.
Zusammenfassung - Das Wichtigste in Kürze
Moment einer Einzelkraft
Ein Moment ist vom Typ "Vektor", hat also einen Betrag, eine Richtung und eine Wirkungslinie.
Eine Einzelkraft hat eine Momentenwirkung. Anders, als beim Kräftepaar, hängt diese Momentenwirkung von der Lage des Bezugspunktes relativ zur Wirkungslinie der Kraft ab.
Geht die Wirkungslinie der Kraft durch den Bezugspunkt, gibt es keine Momentenwirkung, d.h. das Moment ist Null.
Für den Betrag des Momentes gilt:
Der Betrag des Momentes einer Einzelkraft = (senkrechter Abstand zwischen der Wirkungslinie der Kraft und dem Bezugspunkt bzgl. dessen das Moment betrachtet wird) mal (Betrag der Kraft).
Die Kurzform hierfür ist: Moment = (Hebelarm) mal (Kraft).
Für die Richtung des Momentes gilt:
Der Momentenvektor steht immer senkrecht auf der Ebene, die durch die
Richtung der Kraft und die Richtung des Hebelarms aufgespannt wird.
Die Richtung des Momentes wird durch den 'Drehsinn' der Kraft relativ zum gewählten Bezugspunkt bestimmt.
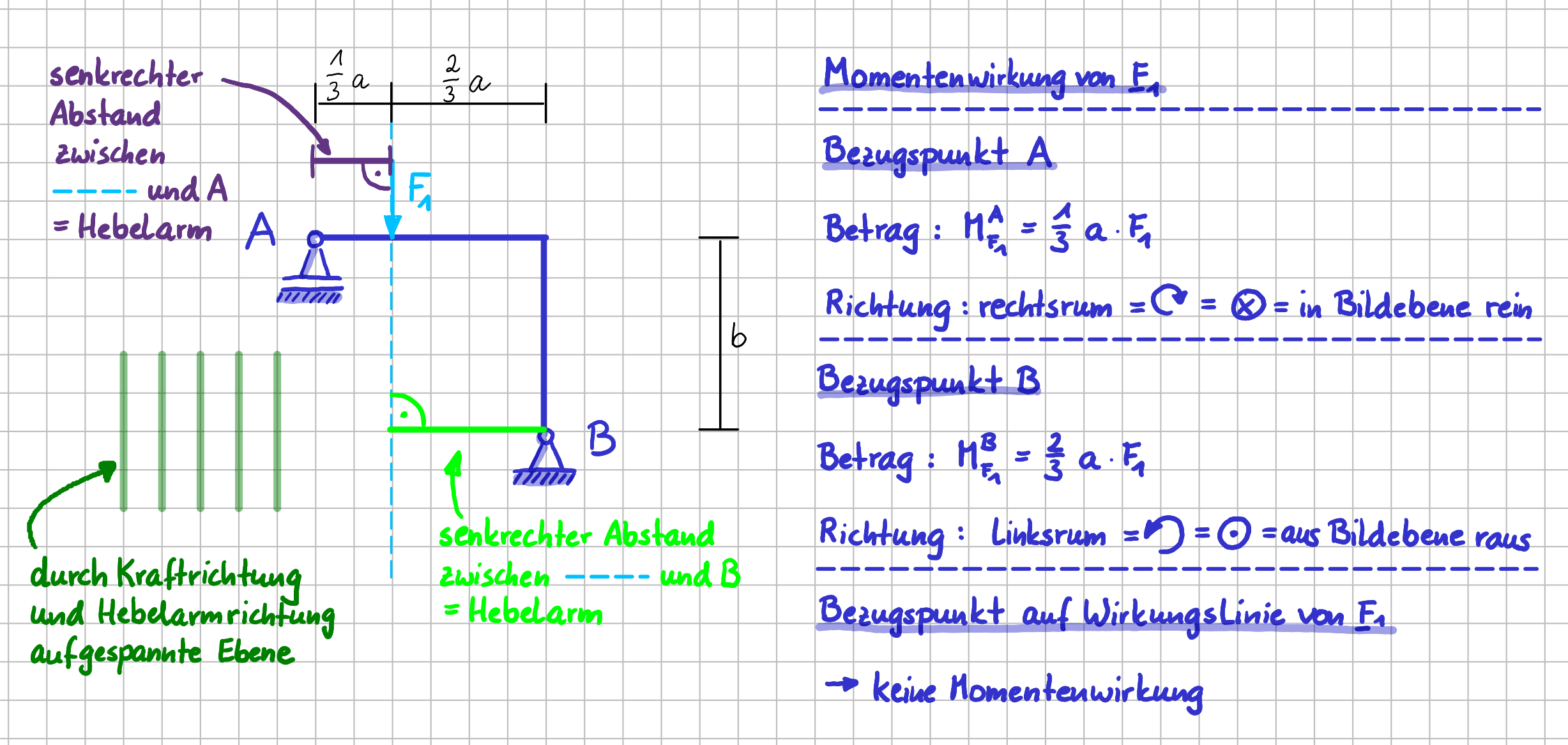
Moment einer Einzelkraft - ebener Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Moment_einer_Einzelkraft_ebener_Fall.png
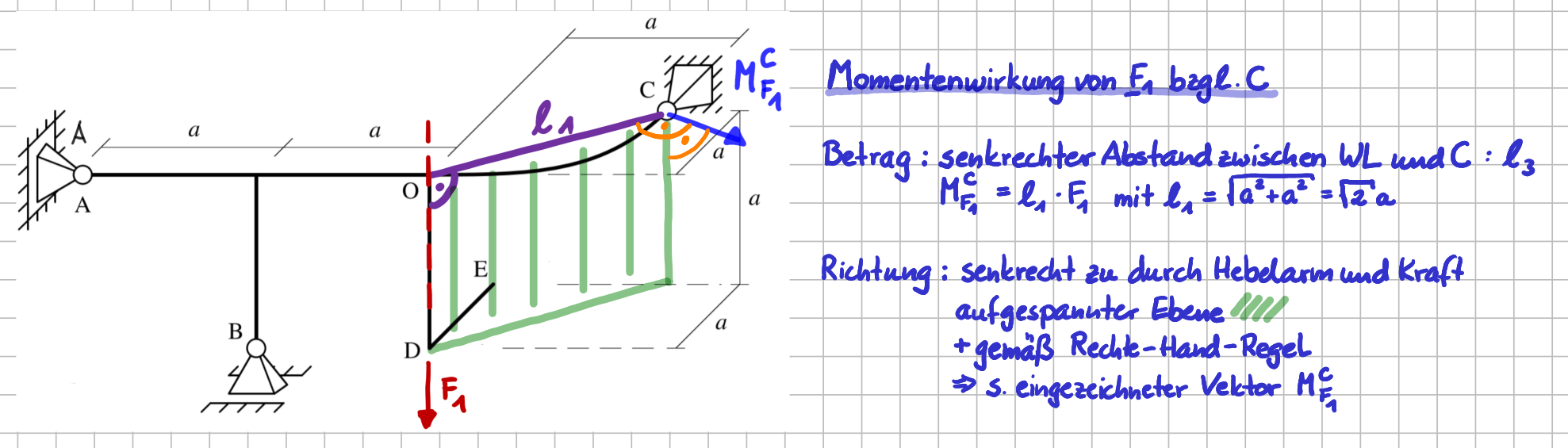
Moment einer Einzelkraft - räumlicher Fall
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Moment_einer_Einzelkraft_raeumlicher_Fall.png
Der Momentenvektor steht immer senkrecht auf der Ebene, die durch die Richtung der Kraft und die Richtung des Hebelarms aufgespannt wird. In welche Richtung entlang der Normalen der Ebene der Momentenvektor zeigt, lässt sich mit der Rechte-Hand-Regel für Momente prüfen.
Schritt 1: Faust der rechten Hand in Momentenbezugspunkt legen
Schritt 2: Daumen in Richtung der Normalen der Ebene ausstrecken (hier gibt es zwei Möglichkeiten). Die Daumenrichtung ist identisch der Momentenrichtung, wenn die restlichen Finger in Richtung der betrachteten Kraft zeigen (und nicht entgegengesetzt).
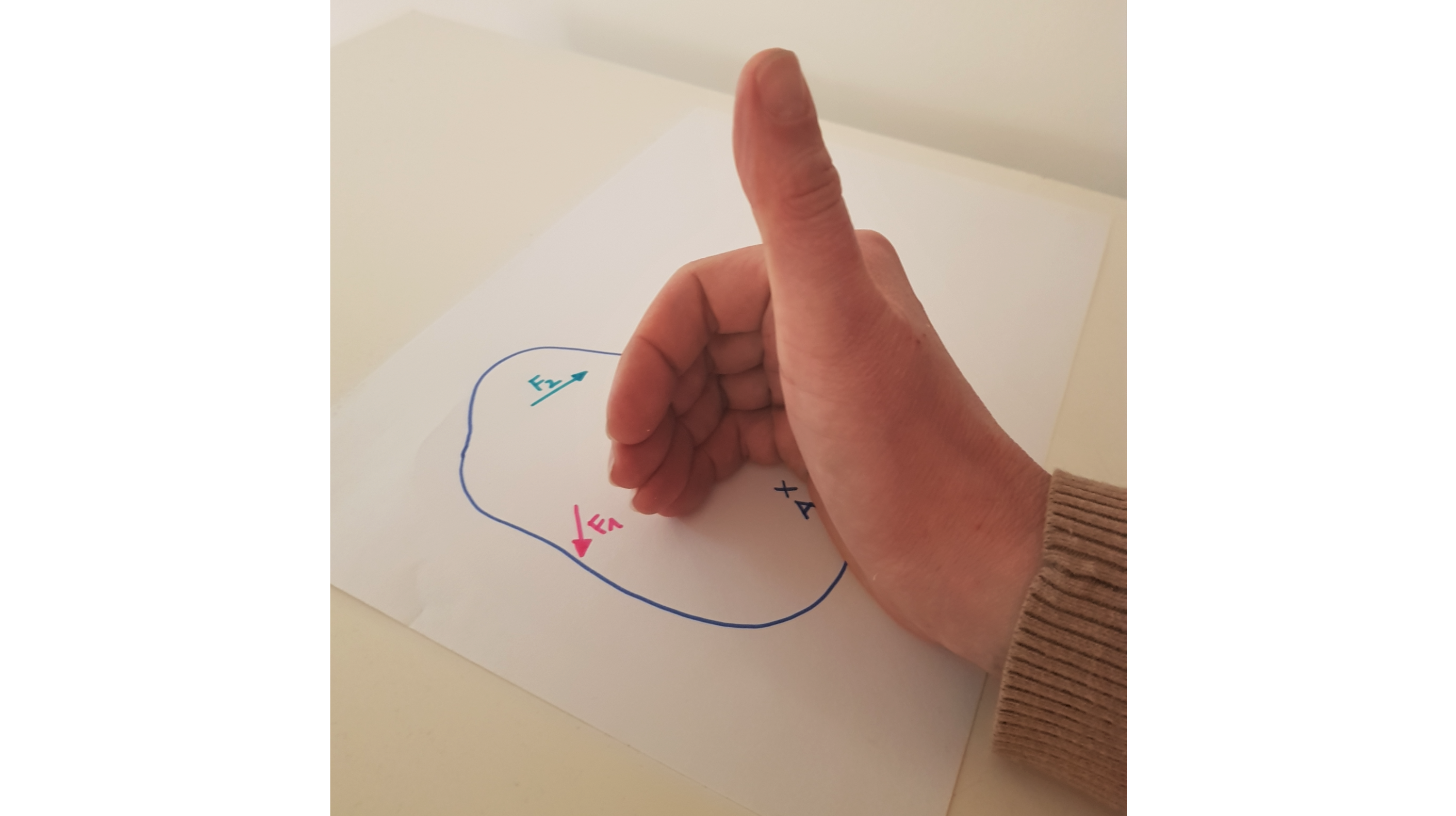
Anwenden der Rechte-Hand-Regel für das Moment zur Bestimmung der Momentenrichtung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2176/Rechte_Hand_Regel_Momentenrichtung%20%281%29.png
Die Richtung des Momentes der Kraft \( F_1 \) bezüglich des Punktes \( A \) ist senkrecht aus der Tischebene raus. Die Richtung des Momentes der Kraft \( F_2 \) bezüglich des Punktes \( A \) ist senkrecht in die Tischebene rein.

