Moment
Moment
2. Moment eines Kräftepaars
2.2. ... mathematisch darstellen
Moment eines Kräftepaars
... mathematisch darstellen
Mit dem mechanischen Verständnis aus dem vorangegangenen Abschnitt im Gepäck weißt du ja schon, in welche Richtung der Vektor zeigt und welchen Betrag er hat. Wenn es jetzt also darum geht, den Vektor mathematisch zu beschreiben, musst du diese Informationen nur noch als Vektor bezüglich eines Koordinatensystems darstellen.Wichtig ist: erst jetzt benötigst du ein Koordinatensystem. Alle Überlegungen zum mechanischen Verständnis haben wir komplett ohne Verwendung eines Koordinatensystems ausgeführt.
Machen wir es gleich konkret und greifbar. Wenn wir für das letzte Beispiel die Momentenvektoren der drei Kräftepaar mathematisch darstellen wollen, brauchen wir als erste ein Koordinatensystem. Dies ist in der folgenden Abbildung bereits eingezeichnet. Grundsätzlich kannst du dir Koordinatensystem wählen, so wie "du lustig bist". An der Mechanik ändert sich dadurch gar nichts. Einzig und allein die mathematische Darstellung kann, je nach gewähltem Koordinatensystem- einfacher oder schwieriger sein.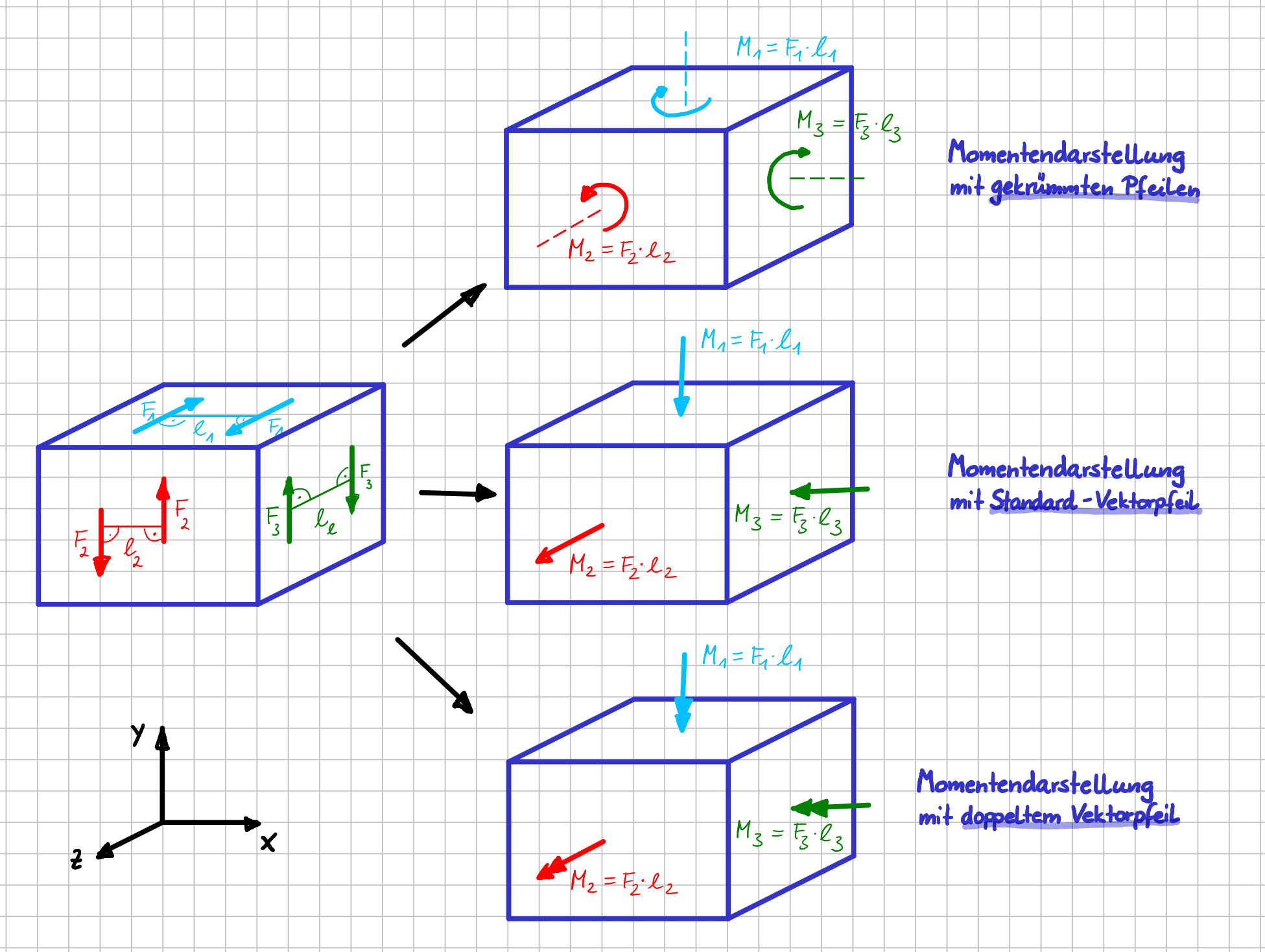
Mathematische Beschreibung der Momentenvektoren dreier verschiedener Kräftepaare
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2175/Kraeftepaare_und_resultierende_Momente_unterschiedliche_Darstellungsarten.png
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_1 \) zeigt in negative \( y \)-Richtung und hat den Betrag \( M_1=\ell_1 \cdot F_1 \). Die Vektordarstellung lautet also:
$$\vec{M}_1= \ell_1 \cdot F_1 \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ - \ell_1 F_1 \\ 0 \end{pmatrix}$$
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_2 \) zeigt in positive \( z \)-Richtung und hat den Betrag \( M_2=\ell_2 \cdot F_2 \). Die Vektordarstellung lautet also:
$$\vec{M}_2= \ell_2 \cdot F_2 \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \ell_2 F_2\end{pmatrix}$$
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_3 \) zeigt in negative \( x \)-Richtung und hat den Betrag \( M_3= \ell_3 \cdot F_3 \). Die Vektordarstellung lautet also:
$$\vec{M}_3= \ell_3 \cdot F_3 \begin{pmatrix} -1\\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -\ell_3 F_3 \\ 0 \\ 0 \end{pmatrix}$$
Und was passiert, wenn du ein anderes Koordinatensystem wählst, z.B. das lila-farbene?
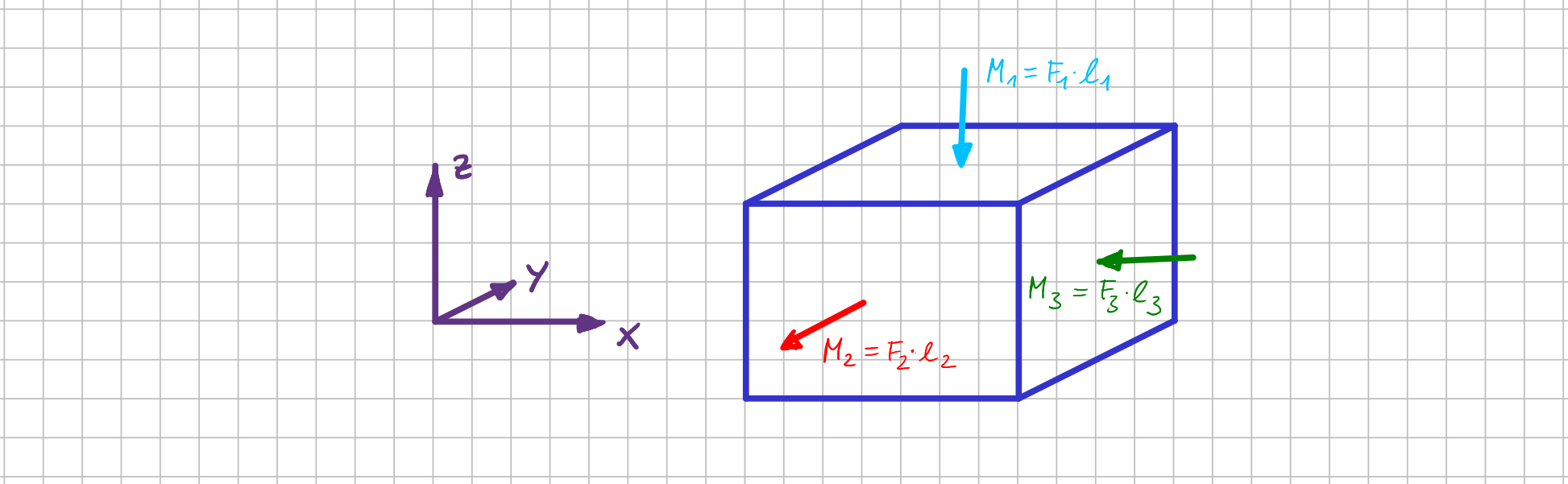
Anderes Koordinatensystem als Basis für die Darstellung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2175/Anderes_Koordinatensystem_als_Basis_fuer_die_Darstellung.png
Am mechanischen Verständnis des Momentes eines Kräftepaars und auch an der physikalischen Richtung des Momentenvektors ändert sich dadurch natürlich gar nichts. Lediglich die mathematische Darstellung ist eine andere.
Es gilt dann:
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_1 \) zeigt in negative \( z \)-Richtung und hat den Betrag \( M_1= \ell_1 \cdot F_1 \). Die Vektordarstellung lautet also:
$$\vec{M}_1= \ell_1 \cdot F_1 \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -\ell_1 F_1 \end{pmatrix}$$
Das Moment des Kräftepaars mit den Kräften \( \vec{F}_2 \) zeigt in negative \( y \)-Richtung und hat den Betrag \( M_2= \ell_2 \cdot F_2 \). Die Vektordarstellung lautet also:$$\vec{M}_2= \ell_2 \cdot F_2 \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ - \ell_2 F_2 \\ 0 \end{pmatrix}$$
Beim Moment des Kräftepaars mit den Kräften \( \vec{F}_3 \) ändert sich nichts, da die Ausrichtung der lila-farbenen und der schwarze \( x \)-Achse identisch ist:
$$\vec{M}_3= \ell_3 \cdot F_3 \begin{pmatrix} -1\\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -\ell_3 F_3 \\ 0 \\ 0 \end{pmatrix}$$
Mit dem mechanischen Verständnis im Kopf, ist die mathematische Beschreibung also 'nur noch' ein Hinschreiben der Vektoren mit Bezug auf das gewählte Koordinatensystem.

