Moment
Moment
2. Moment eines Kräftepaars
2.1. ... mechanisch verstehen
Moment eines Kräftepaars
... mechanisch verstehen
Du hast bestimmt schon mal mit einem Schraubendreher von Hand eine Schraube angezogen, oder?
Schließ mal kurz die Augen und stell dir vor, was du beim Anziehen in der Hand, die den Schaft des Schraubendrehers hält, spürst.
Tada..... genau das, was du da wahrnimmst, ist ein Moment.
Soweit ganz einfach, oder?

Anziehen einer Schraube mit einem Schraubendreher
Weitere Informationen
Simone D. McCourtie
CC BY-NC-ND 2.0
https://www.flickr.com/photos/10816734@N03/3963500758
Und was hat das jetzt mit einem Kräftepaar zu tun?
Wir stellen uns vor, dass die Schraube schon ein Stück ins Werkstück eingeschraubt ist und dass du gerade ein so großes Moment mit deiner Hand aufbringst, dass der Schraubendreher die Schraube gerade noch nicht weiter in das Werkstück reindreht. Dann sind wir noch im Bereich der Statik. (Würdest du ein minimal größeres Moment mit deiner Hand aufbringen, käme der Schraubendreher in Bewegung und wir wären im Bereich der Dynamik.)
Das, was du mit der Hand aufbringst, ist das Moment \( M_{\mathrm{Hand}} \). Da das Moment eine Drehbewegung bewirken würde, ist es naheliegend, für das Moment einen 'gekrümmten' Pfeil zu verwenden, wie er in der Zeichnung links in grün eingezeichnet ist.
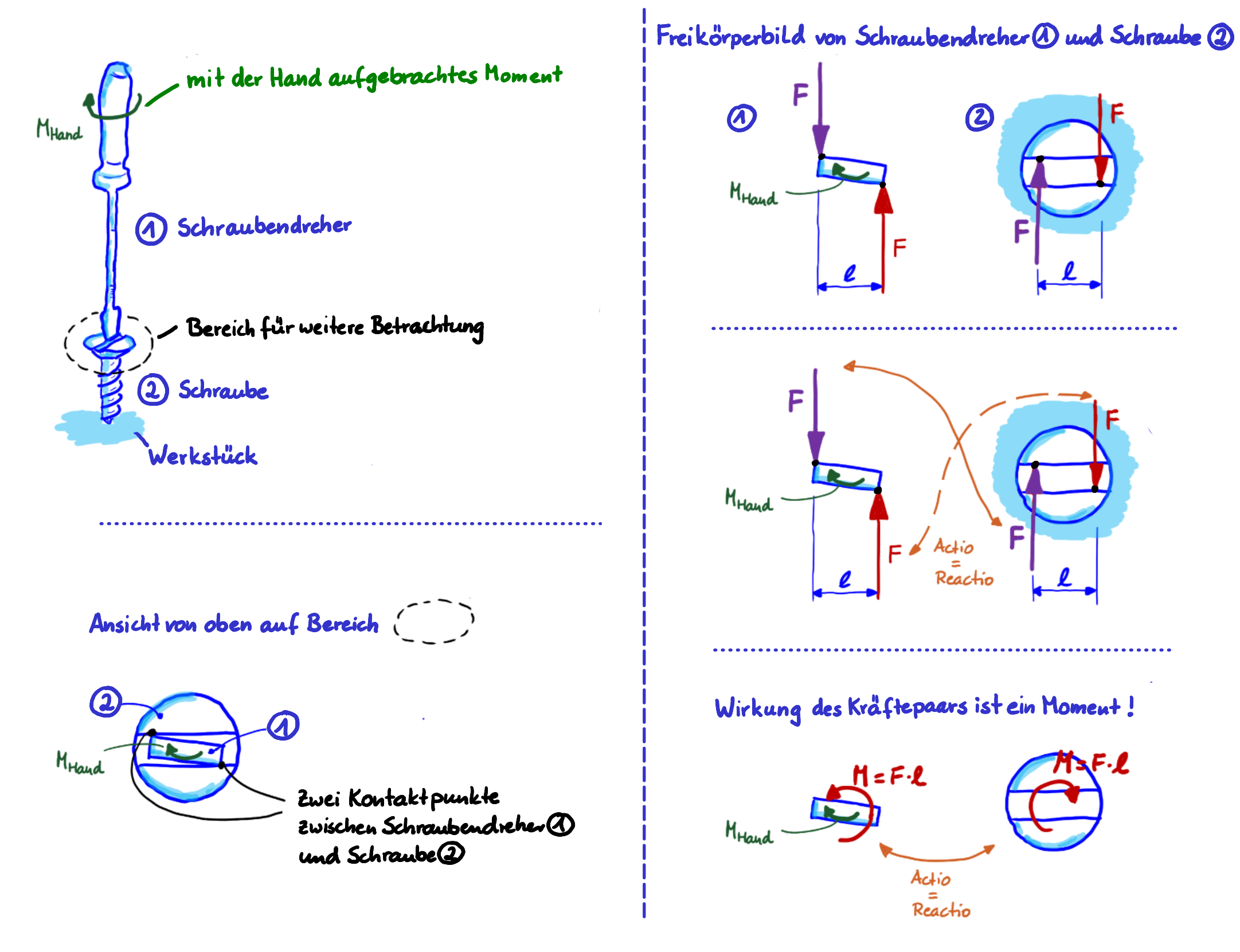
Kräftepaar und Moment beim Schlitzschraubendreher
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2174/Kraeftepaar_und_Moment_beim_Schlitzschraubendreher%20%281%29.png
Schauen wir jetzt mal genau in den Kontaktbereich zwischen Schraubendreher und Schraube. Die Schraubendreherspitze berührt den Schlitz der Schraube in genau zwei Kontaktpunkten.
Wenn wir das Gesamtsystem an dieser Stelle trennen, also ein Freikörperbild des Schraubendrehers zeichnen und auch den Schraubenkopf separat darstellen, dann wirken auf den Schraubendreher das Moment \( M_{\mathrm{Hand}} \) und zwei Kräfte mit Betrag \( F \) an den Kontaktpunkten. Die Richtung der beiden Kräfte ist senkrecht zum Schlitz und der Abstand der beiden Kontaktpunkte ist wie eingezeichnet \( \ell \).
Und da ist es, das Kräftepaar. Tada.
Da der Schraubendreher im Gleichgewicht ist \( - \) er bewegt sich ja nicht \( - \), muss die resultierende Wirkung aller angreifenden Größen ( \( M_{\mathrm{Hand}} \) und Kräfte \( F \) ) im Gleichgewicht sein.
Für die Summe aller angreifenden Kräfte, also das Kräftegleichgewicht, gilt: \( F-F=0 \).
Ein Kräftepaar hat also keine resultierende Kraftwirkung auf den Körper.
Nun wirkt ja aber nachweislich das Moment deiner Hand an dem Schraubendreher. Also muss aus dem Kräftepaar ein dem Moment \( M_{\mathrm{Hand}} \) entgegengesetzt gerichtetes Moment resultieren. Sonst könnte der Schraubendreher ja gar nicht im Gleichgewicht sein. Und genau so ist es. Für das Momentengleichgewicht gilt: \( M_{\mathrm{Hand}}=F\cdot \ell=M_{\mathrm{Kräftepaar}} \).
Ein Kräftepaar hat also als Wirkung auf den Körper ausschließlich ein Moment, das den Betrag "Kraft mal senkrechter Abstand der Wirkungslinien der Kräfte" hat. Seine Richtung ist durch die Richtung der Kräfte gegeben: In diesem Beispiel "drehen" die beiden Kräfte linksrum. Das Moment, das du mit der Hand aufbringst, wirkt genau andersrum.
Übertragen wir das Gelernte noch auf die vier Kräftepaare aus dem Beispiel:
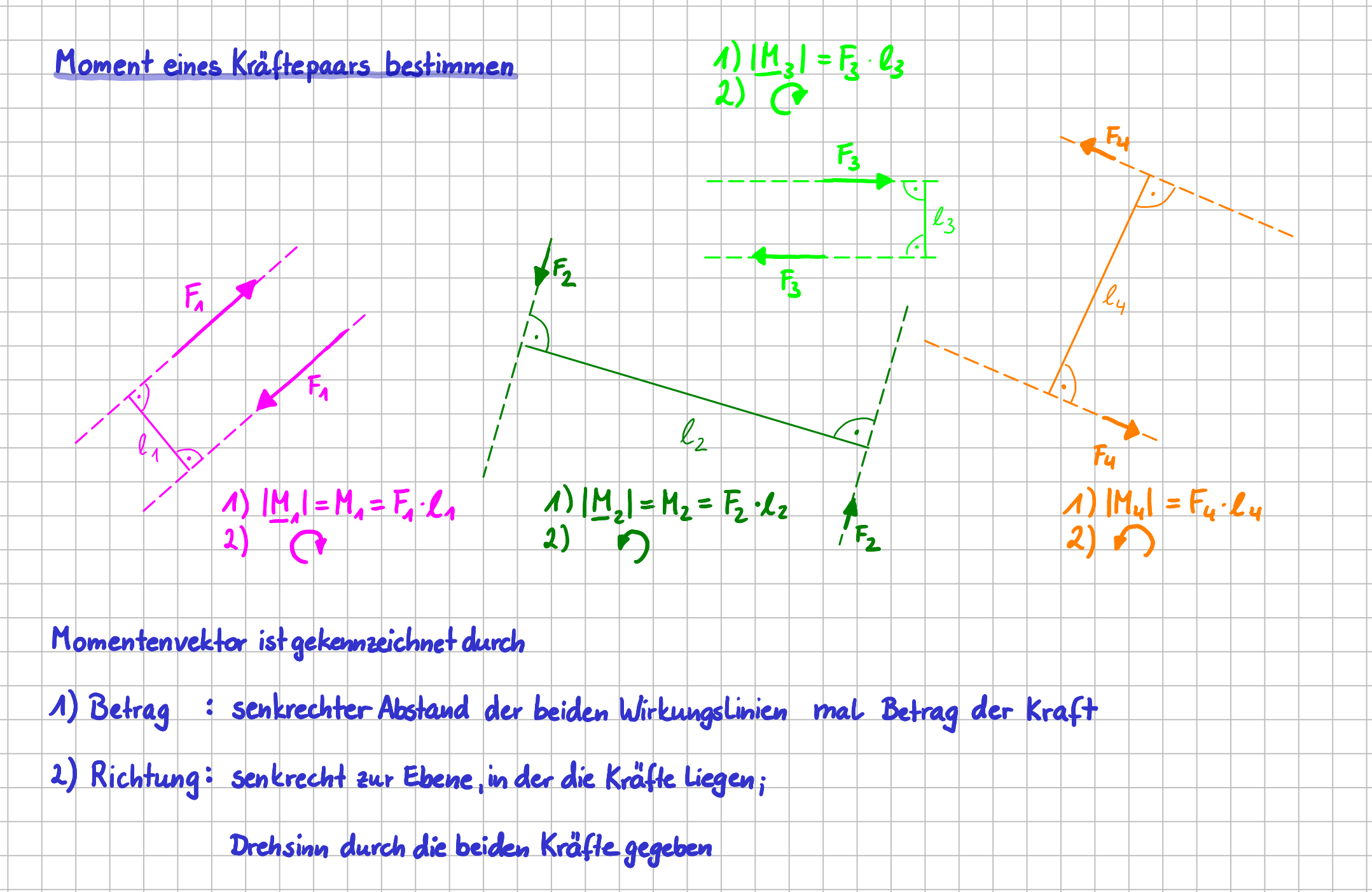
Resultierende Momente für vier verschiedene Kräftepaare
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2174/resultierende_Momente_fuer_vier_verschiedene_Kraeftepaare.png
Zusammenfassung - Das Wichtigste in Kürze
Ein Kräftepaar ist gekennzeichnet durch zwei Kräfte,
- die denselben Betrag haben,
- deren Wirkungslinien parallel sind und
- deren Richtungen entgegengesetzt sind.
Das Moment eines Kräftepaars ist - wie jeder Momentenvektor - gekennzeichnet durch seinen Betrag und seine Richtung:
- Betrag = 'senkrechter Abstand zwischen den Wirkungslinien der beiden Kräfte mal Betrag der Kraft'
- Richtung = 'senkrecht zu der Ebene, in der das Kräftepaar liegt und mit 'Drehsinn' gemäß dem Kräftepaar'
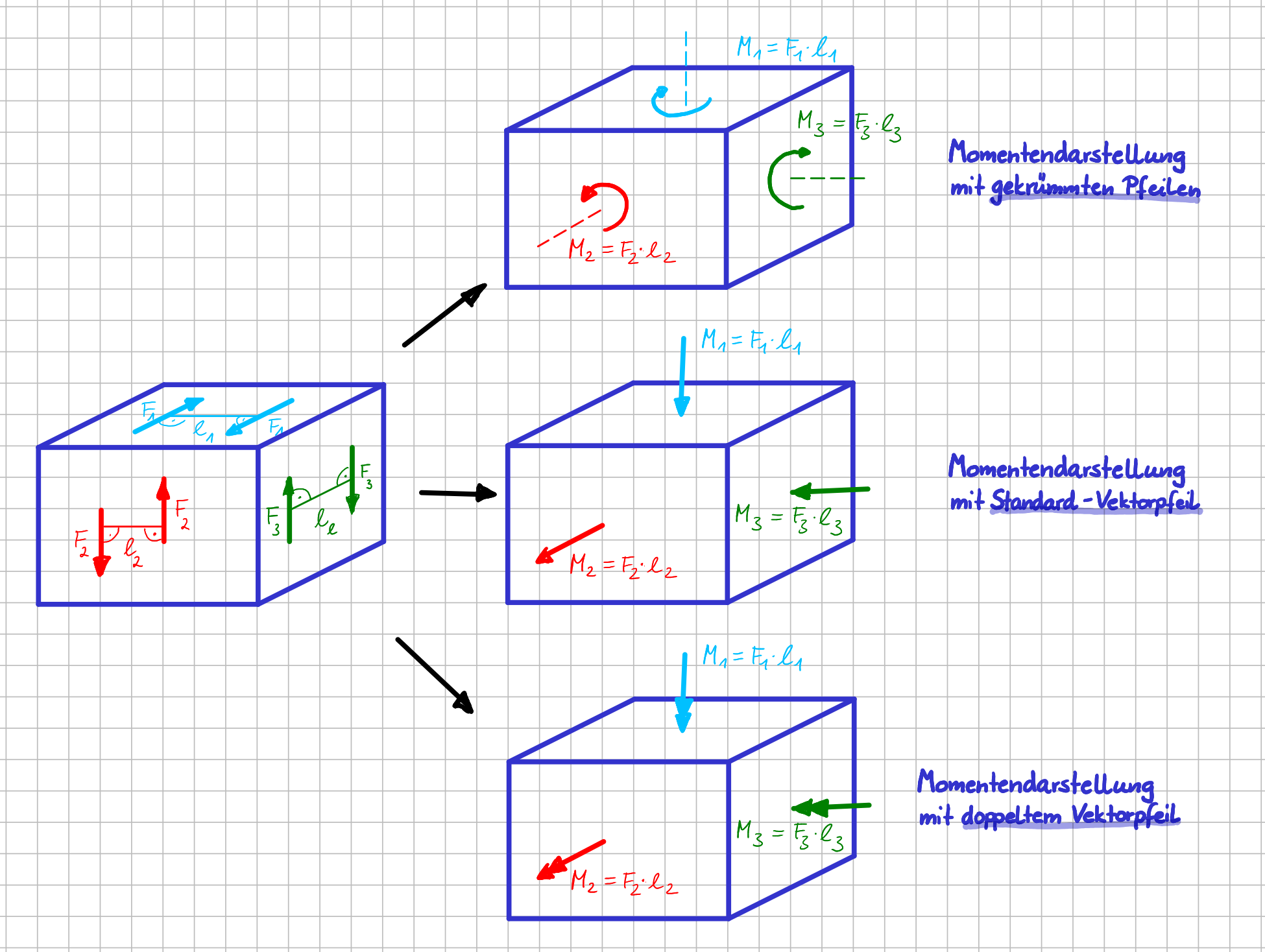
Kräftepaare und resultierende Momente mit unterschiedlichen Darstellungsarten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13818/mod_book/chapter/2174/Kraeftepaare_und_Momente_verschiedene_Darstellungsformen.png

