Kraftzerlegung

Wenn du Mechanikaufgaben lösen willst, wirst du immer wieder Kräfte in ihre Komponenten bezüglich der gegebenen Koordinatenachsen zerlegen. Weil es so oft vorkommt, solltest du dieses Vorgehen quasi im Schlaf beherrschen. Deswegen wollen wir uns in diesem Abschnitt genau anschauen, wie das eigentlich geht.

Was du an mathematischem Werkzeug mitbringen solltest: Sicher mit den Winkelfunktionen Sinus und Cosinus umgehen können. Schau gerne nochmal im Kapitel Tirgonometrie vorbei, wenn du das erst noch üben willst: Hier geht's zum Kapitel Trigonometrie.

In der folgenden Abbildung links siehst du einen Balken, der an der linken Seite fest eingespannt ist. Er ist im Punkt  \(B\)   mit der Kraft  \(\vec{F}\)  belastet. Die Kraft greift unter dem Winkel  \(\delta\)  zur Horizontalen an. Auf der rechten Seite ist die Kraft  \(\vec{F}\)  in ihre Komponenten zerlegt worden.

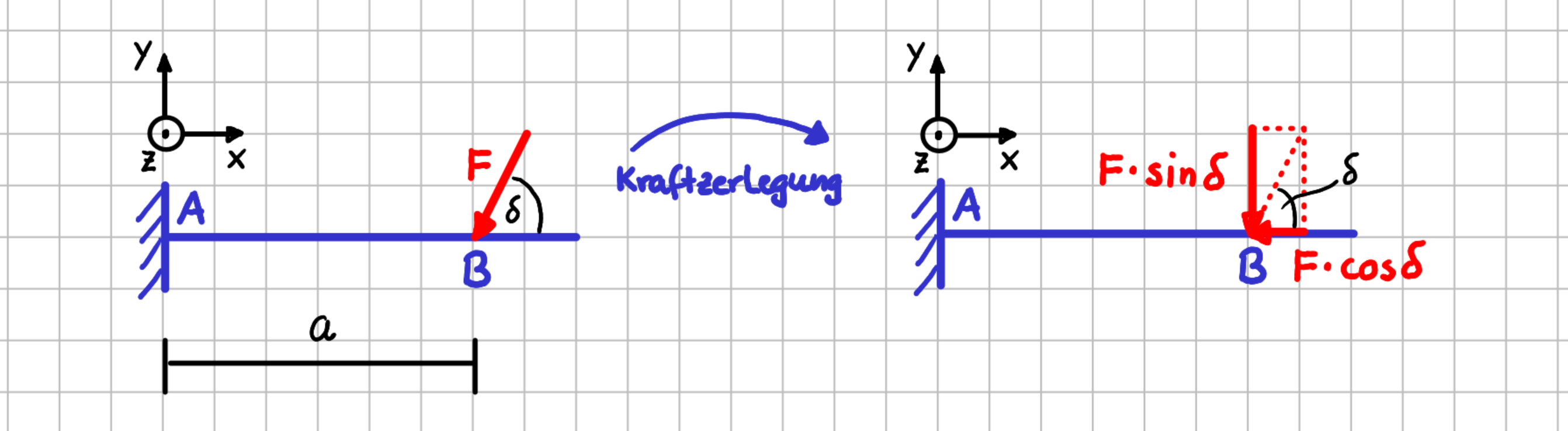
Kraftzerlegung

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2173/Kraftzerlegung.png

Warum muss die Kraft jetzt überhaupt zerlegt werden?
Wenn du die Lagerkräfte für dieses System berechnen willst, musst du nach dem Erstellen des Freikörperbildes unter anderem das Kräftegleichgewicht aufstellen. Dazu muss du wissen, wie groß die die Anteile von  \(\vec{F}\)  in die  \(x-\)  und  \(y-\) Richtung sind.

Wie das mit der Kraftzerlegung genau geht, siehst du in der folgenden Abbildung. Es sind vier Schritte, die du durchläufst. Ich empfehle dir, am Anfang die Schritte wirklich so ausführlich hinzuschreiben bzw. hinzuzeichnen, wie ich es getan habe. Später wirst du das vermutlich alles im Kopf machen.

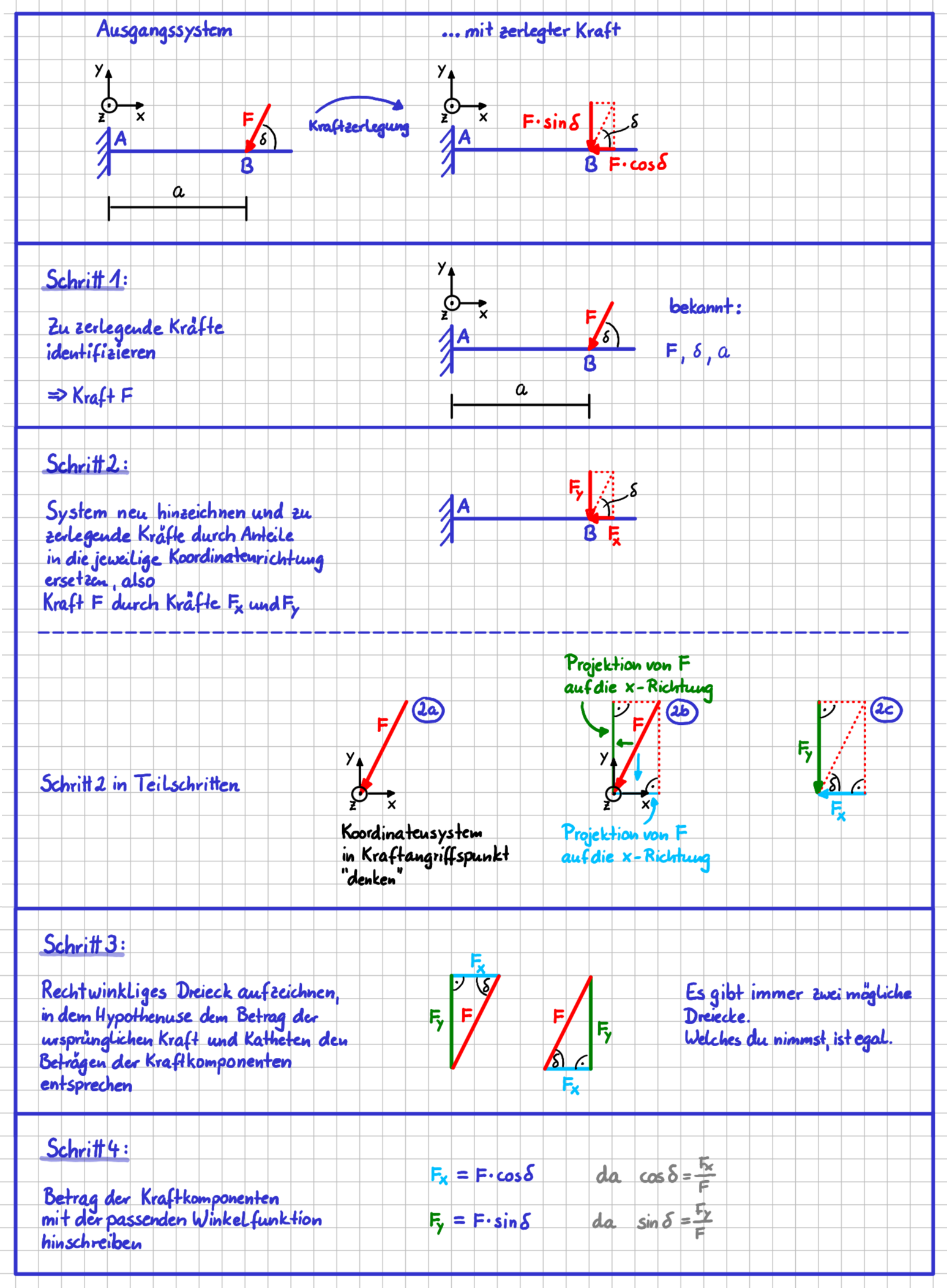
Kraftzerlegung Schritt für Schritt

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2173/Kraftzerlegung_Schritt_fuer_Schritt%20%281%29.png

Worauf kommt es an? Ganz wichtig ist, dass du dir klarmachst, dass du in Schritt 2 eine Vektoroperation an einem Kraftvektor, also einem gebundenen Vektor durchführst. Diese Zerlegung musst du im Angriffspunkt der Kraft durchführen. Das bedeutet, dass die beiden Kraftkomponenten, die du durch die Zerlegung bekommst, mit ihren Pfeilspitzen auf den Kraftangriffspunkt zeigen.

In Schritt 3 führst du keine Vektoroperation, sondern eine rein geometrische Betrachtung durch, um die Beträge der beiden Vektorkomponenten zu bestimmen. Hier schaust du dir also reine Streckenlängen an. Du wählst dabei eines der beiden sich ergebenden rechtwinkligen Dreiecke aus. Der Betrag der ursprünglichen Kraft ist die Hypothenuse in diesen Dreiecken. Die Beträge der Komponenten entsprechen den Längen der Katheten.

Schritt 4 ist ein rein mathematischer Schritt, in dem du die trigonometrischen Beziehungen beim rechtwinkligen Dreieck verwendest, um die Länge der beiden Katheten in Abhängigkeit von gegebenem Winkel und Hypothenuse anzugeben.

Wenn du dich jetzt fragst: "Und was mache ich, wenn der Kraftangriffspunkt nicht auf dem Bauteil liegt?", dann ist das eine berechtigte Frage. Du hast ja im vorangegangenen Abschnitt gerade gesehen, dass es gewisse Operationen bei gebundenen Vektoren wie Kräften gibt, die du durchführen darfst, ohne dass sich die Wirkung nach Außen ändert.

Schauen wir uns das anhand des folgenden Beispiels mal genauer an.

xxx BILD 1

Du kannst eine Kraft ja entlang ihrer Wirkungslinie verschieben. Wenn du das tust, so dass der Kraftangriffspunkt auf dem Bauteil liegt, sieht die Kraftzerlegung auch nicht mehr "komisch" aus.