Kraft
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Kraft |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 12:49 |
1. Einleitung
Einleitung Kraft
In dieser Lektion nehmen wir die physikalische Größe Kraft ganz genau unter die Lupe. Wir schauen uns an, was eine Kraft überhaupt ist, wie man Kräfte darstellen kann, um dann auch Berechnungen durchzuführen.
Und wir steigen ein in die Modellierung: Wir wollen ja versuchen, reale Systeme mathematisch zu beschreiben. Du wirst sehen: In der Statik gibt es verschiedene Operationen, die du in deinen Modellen mit Kräften ausführen kannst und die dir das Lösen von Aufgaben erheblich vereinfachen.
Wir schauen, welche verschiedenen Arten von Kräften es gibt. Und wir analysieren, was die Merkmale für ebene und für räumliche Kräftesysteme sind.

Die 'magische' Größe Kraft: unsichtbar aber dennoch mit unglaublicher Wirkung
Weitere Informationen
2. Grundlagen
Grundlagen Kraft
In diesem ersten Abschnitt geht es um die Beschreibung und Darstellung von Kräften. Wir schauen uns an, was ein Kräftesystem ist und welche Arten es gibt. Und du bekommst eine Übersicht darüber, welche Kraftarten es in der Realität gibt und welche Arten typischer Weise in mechanischen Modellen verwendet werden.
2.1. Beschreibung und Darstellung
Beschreibung und Darstellung von Kräften
Kräfte sind vektorielle Größen. Sie lassen sich also als Vektor mit Betrag und Richtung darstellen. Genauer gesagt sind Kräfte gebundenen Vektoren. Aber der Reihe nach.
Stell dir vor, du bist die Person auf dem folgenden Bild. Plötzlich kommt Wind auf und die Kraft, die eine Böe auf dich ausübt, hat eine Größe von \(200\mathrm{N}\). Es macht einen erheblichen Unterschied, ob diese Kraft von links oder von rechts auf dich einwirkt, oder? Einmal geht es für dich Richtung Sicherheit, einmal Richtung Abgrund.

Die Richtung einer Kraft macht den Unterschied
Weitere Informationen
Kräfte sind nicht nur Vektoren, sie sind gebundene Vektoren.
Was ist das denn nun schon wieder? Und gibt es dann auch
ungebundene/freie Vektoren? Ja, die gibt es. Aber da Kräfte nun mal
gebundene Vektoren sind, konzentrieren wir uns erst einmal darauf.
Mit der Gewichtskraft lässt sich sehr einfach veranschaulichen, was es bedeutet, dass die Kraft ein gebundener Vektor ist.
Stell dir ein Pendel vor. Das kann z.B. ein Stein an einem Faden oder ein Lot auf einer Baustelle sein. Wenn du dieses Pendel auslenkst, dann schwingt es hin und her.
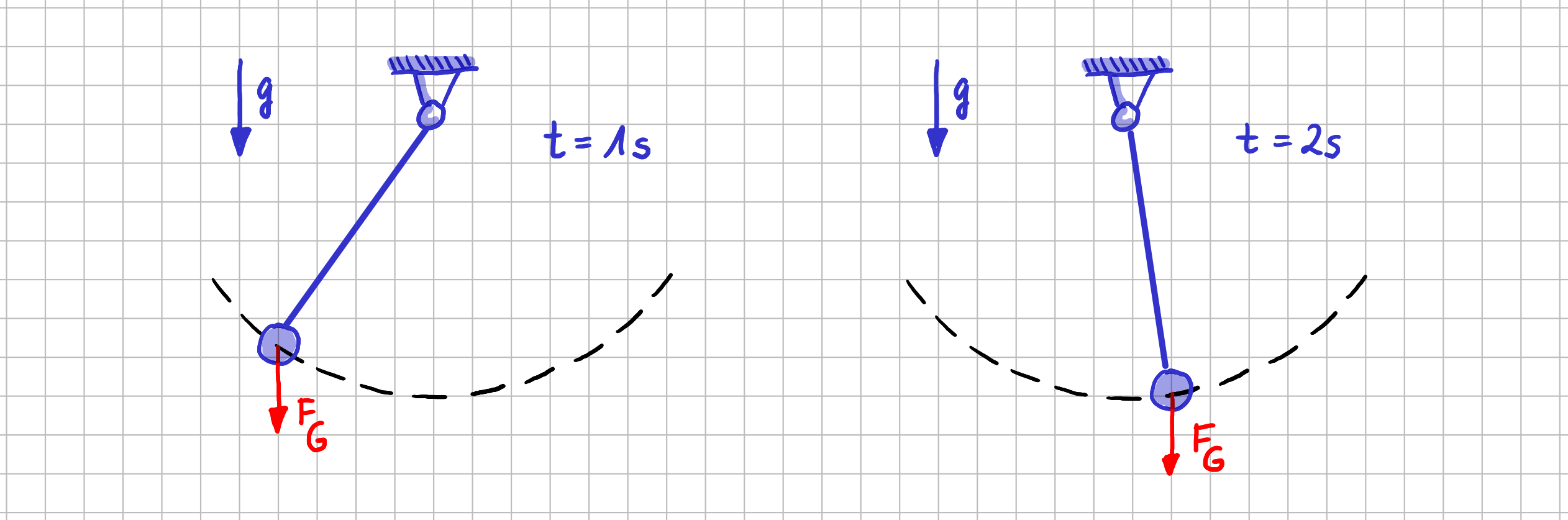
Kraft als gebundener Vektor am Beispiel der Gewichtskraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2163/Kraft_als_gebundener_Vektor_am_Beispiel_Gewichtskraft.png
Das Pendelobjekt (Stein oder Senkblei) hat aufgrund seiner Masse \( - \)nehmen wir an es seien \( 500\mathrm{g} \) \( - \) eine Gewichtskraft von \( 0,5\mathrm{kg} \cdot 9,81 \frac{\mathrm{kg}}{\mathrm{m} \cdot \mathrm{s}^2} \approx 5\mathrm{N} \). Und der Angriffspunkt dieser Masse "bewegt sich mit dem Objekt mit". Um die Gewichtskraft korrekt beschreiben zu können, braucht es also zusätzlich zu Betrag \( 5\mathrm{N} \) und Richtung (in Richtung des Erdmittelpunktes, also in Richtung des Vektors der Erdbeschleunigung \( \vec{g} \) ) auch noch den Angriffspunkt des Vektors. Und dieser Angriffspunkt ist der Schwerpunkt des Pendelobjektes.
Für einen gebundenen Vektor sind also drei Informationen erforderlich:
- Betrag,
- Richtung und
- Lage des Angriffspunktes.
Wenn du einmal am eigenen Körper spüren willst, genauer gesagt in deinem Schultergelenk, dass die Kraft ein gebundener Vektor ist, ihre Wirkung also von der Lage des Angriffspunktes abhängt, dann mach doch einfach mal den folgenden Versuch.
Streck beide Arme seitlich aus. Jetzt bittest du jemand, mit der gleichen Kraft beim rechten Arm auf dein Handgelenk nach unten zu drücken, und linken Arm auf dein Schultergelenk. Dein Aufgabe ist es, beide Arme in der horizontalen Position zu halten.
Die beiden Kräfte sind dann gleich, was den Betrag und die Richtung angeht. Nur ihr Angriffspunkt relativ zum Schultergelenk ist unterschiedlich.

Die Lage des Angriffspunktes hat auf die Wirkung einer Kraft einen großen Einfluss.
Weitere Informationen
yanalya, Zuschnitt und Eintragungen Johanna Peters
Freepik-Lizenz
https://de.freepik.com/fotos-kostenlos/glueckliches-maedchen-zeigt-zwei-uebungen-fuer-arme_937106.htm
Na, merkst du die unterschiedliche Wirkung der beiden Kräfte?
Wenn du dich auf deine Schultergelenke konzentriertst, merkst du sie daran, dass du auf der rechten Seite über die Muskeln rund um das Schultergelenk ein Moment aufbringen musst, um die Abwärtsbewegung (Drehung) des Arms zu verhinden und den Arm in der horizontalen Lage zu halten. Auf der linken Seite ist das nicht nötig.
Wenn du die Informationen für einen gebundenen Vektor wie z.B. die Kraft angeben willst, reicht es also nicht aus, den Betrag und den Kraftvektor an sich aufzuschreiben. Du musst zusätzlich noch die Lage des Angriffspunktes kennen.
Für einen allgemeinen Kraftvektor sieht das dann so aus, wenn wir der Einfachheit der Darstellung halber mal annehmen, dass der Kraftvektor in der \(xy-\)Ebene wirkt.

Darstellung eines allgemeinen Kraftvektors (gebundener Vektor) mit Angabe von Betrag, Richtung und Lage des Angriffspunktes
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2163/Darstellung_eines_allgemeinen_Kraftvektors_als_gebundener_Vektor.png
Im Kapitel "Moment" kannst du dich ausführlich auch mit der Momentenwirkung von Kräften beschäftigen. Momente sind auch vektorielle Größen. Allerdings sind sie im Gegensatz zu Kräften ungebunde Vektoren.
Zusammenfassung - Das Wichtigste in Kürze
Kräfte sind ortsgebundene Vektoren.
Für ihre Beschreibung sind daher drei Angaben erforderlich
- der Betrag
- die Richtung
- der Angriffspunkt

Gewichtskraft eines Containers als Beispiel für einen gebundenen Vektor
Weitere Informationen
Kevin Hackert, handschriftliche Ergänzungen von Johanna Peters TUHH
CC BY-NC 2.0
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2163/Gewichtskraft_eines_Containers.png
2.2. Ebenes und räumliches Kräftesystem
Ebenes und räumliches Kräftesystem
Wenn auf einen Körper mehrere Kräfte wirken, so nennt man all diese Kräfte zusammen Kräftesystem.
In der Mechanik werden Kräftesysteme in Bezug auf ihre Dimension unterschieden:
es gibt ebene Kräftesysteme, oft als 2D-Systeme bezeichnet, und räumliche Kräftesysteme, oft als 3D-Systeme bezeichnet.
Gleich vorweg: Die Bezeichnungen "2D" und "3D" können irreführend sein: Sie suggerieren vielleicht, dass die Systeme dahingehend unterschieden werden, ob die betrachteten Körper und Elemente zweidimensional oder dreidimensional modelliert werden können; aber genau darum geht es eben nicht. Also: schau dir im Folgenden erst an, was mit "Dimension" im Kontext von Kräftesystemen in der Mechanik überhaupt gemeint ist. Dann entscheide selbst, welche Begriffe du verwendest, um Kräftesysteme zu charakterisieren. Mit "eben" und "räumlich" liegst du in jedem Fall immer auf der sicheren Seite.
Ebenes Kräftesystem
Ein ebenes Kräftesystem kannst du daran erkennen, dass die Wirkungslinien aller Kräfte in einer Ebene liegen.
In den beiden gezeigten Beispielen handelt es sich beide Male um einen räumlichen Körper.
Aber die Belastungen sind unterschiedlich:
- im linken System wirken die Kräfte alle in der \( xy- \)Ebene, d.h. also, dass ihre Wirkungslinien alle in der \( xy- \)Ebene liegen. Außerdem sind die Ortsvektoren der Kräfte alle in der \( xy- \)Ebene. Es handelt sich also um ein ebenes Kräftesystem.
- im rechten System lliegen die Wirkungslinien der Kräfte nicht mehr alle in einer Ebene. Zusätzlich wirken auch Kräfte in \( z- \)Richtung. Das ist also kein ebenes Kräftesystem mehr, sondern ein räumliches Kräftesystem.
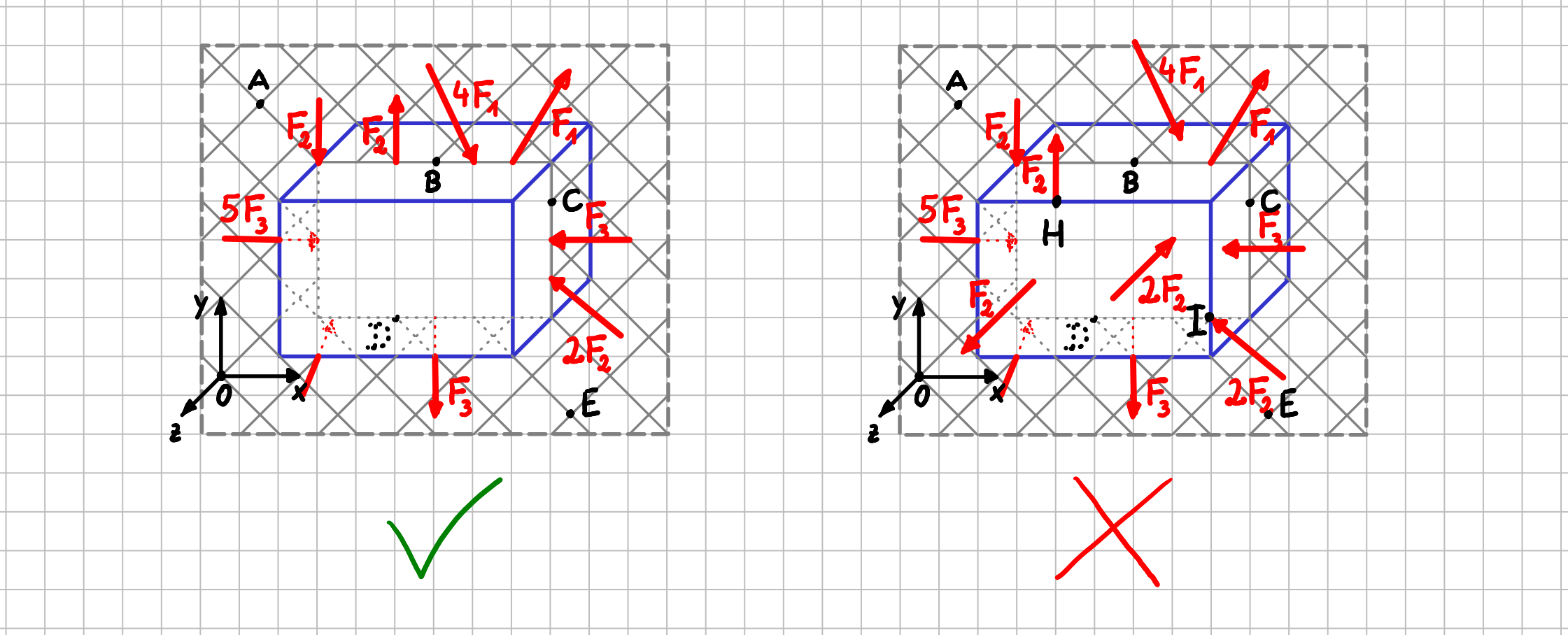
Abgrenzung ebenes Kräftesystem (links) und räumliches Kräftesystem (rechts)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/Abgrenzung_ebenes_rauemliches_Kraeftesystem.png
Wenn du jetzt denkst, "Moment mal, es gibt doch auch noch Momente?!?", dann liegst du genau richtig. Kräfte, die in der \( xy- \)Ebene liegen, haben \( - \) je nach gewähltem Bezugspunkt \( - \) eine Momentenwirkung um die \( z- \)Achse. In einem ebenen Kräftesystem können aber auch noch freie Einzelmomente um die \( z \)-Achse auftreten. Wenn du jetzt etwas entrüstet sagst: "Aber dann gibt es ja doch etwas, was außerhalb der \( xy- \)Ebene, also in \( z -\)Richtung wirkt!", dann hast du nur im ersten Moment recht. Ein Einzelmoment um die \( z- \)Achse ist ja die Wirkung eines Kräftepaars. Und diese beiden Kräfte liegen dann wieder in der \( xy- \)Ebene.
Machen wir es konkret: Die beiden Kräfte '\( 4F_2 \)' bilden genau so ein Kräftepaar. Was waren nochmal die Bedingungen für ein Kräftepaar? 1) Der Betrag der beiden Kräfte ist gleich groß; 2) die Wirkungslinien sind parallel; 3) die Kräfte wirken in die entgegengesetzte Richtung. All das ist hier für die beiden Kräfte '\( 4F_2 \)' gegeben. Ihre Wirkung ist also einzig und allein ein Moment, das um die \( z- \)Achse wirkt; die Ursache, die beiden Kräfte selbst, liegt aber in der \( xy-\)Ebene.
Hier findest du alles aus dem bisherigen Abschnitt auch noch einmal im Video erklärt:
Schauen wir uns noch ein reales System an. Wie kannst du entscheiden, ob du ein reales System als ein ebenes oder als ein räumliches System modellieren kannst? Es hängt einzig und allein davon ab, was du untersuchen möchtest.
Wenn dich bei der dargestellten Brücke z.B. 'nur' die Belastungen der Seile oder Lager aufgrund der Belastungen durch das Eigengewicht der Brücke und dem Verkehr interessiert, reicht es aus, die Brücke als ebenes System zu modellieren: Alle genannten Kräfte liegen in der Brückenebene.
Wenn dich jedoch auch noch interessiert, welchen Einfluss Windlasten haben, die ja je nach Windrichtung aus allen möglichen Richtungen kommen können, musst du die Brücke als räumliches System modellieren: Es treten dann in jedem Fall auch noch Kraftkomponenten senkrecht zur Brückenebene auf.

Brücke mit Eigengewicht und Belastung durch Fahrzeuge
Weitere Informationen
Leonardo Pallotta
CC BY 2.0
https://www.flickr.com/photos/83265757@N00/73471268
Räumliches Kräftesystem
Nachdem jetzt klar ist, was ein ebenes Kräftesystem ist, ist die Definition eines räumlichen Kräftesystems eigentlich schon ein Selbstgänger, oder?
Bei einem räumlichen Kräftesystem können die Wirkungslinien der Kräfte Komponenten in alle drei Koordinatenrichtungen haben.
Ein Beispiel ist das rechte System im vorletzten Bild. Oder ein fahrendes Auto, bei dem der Wind von schräg vorne kommt: die Gewichtskraft \( F_G \) wirkt in \( y- \) Richtung. Die aus dem Wind resultierende Kraft \( F_W \) liegt in der \( xz- \)Ebene und kann in ihre Komponenten \( F_{w_x} \) und \( F_{w_z} \) in \( x-\) und \( z- \)Richtung zerlegt werden.
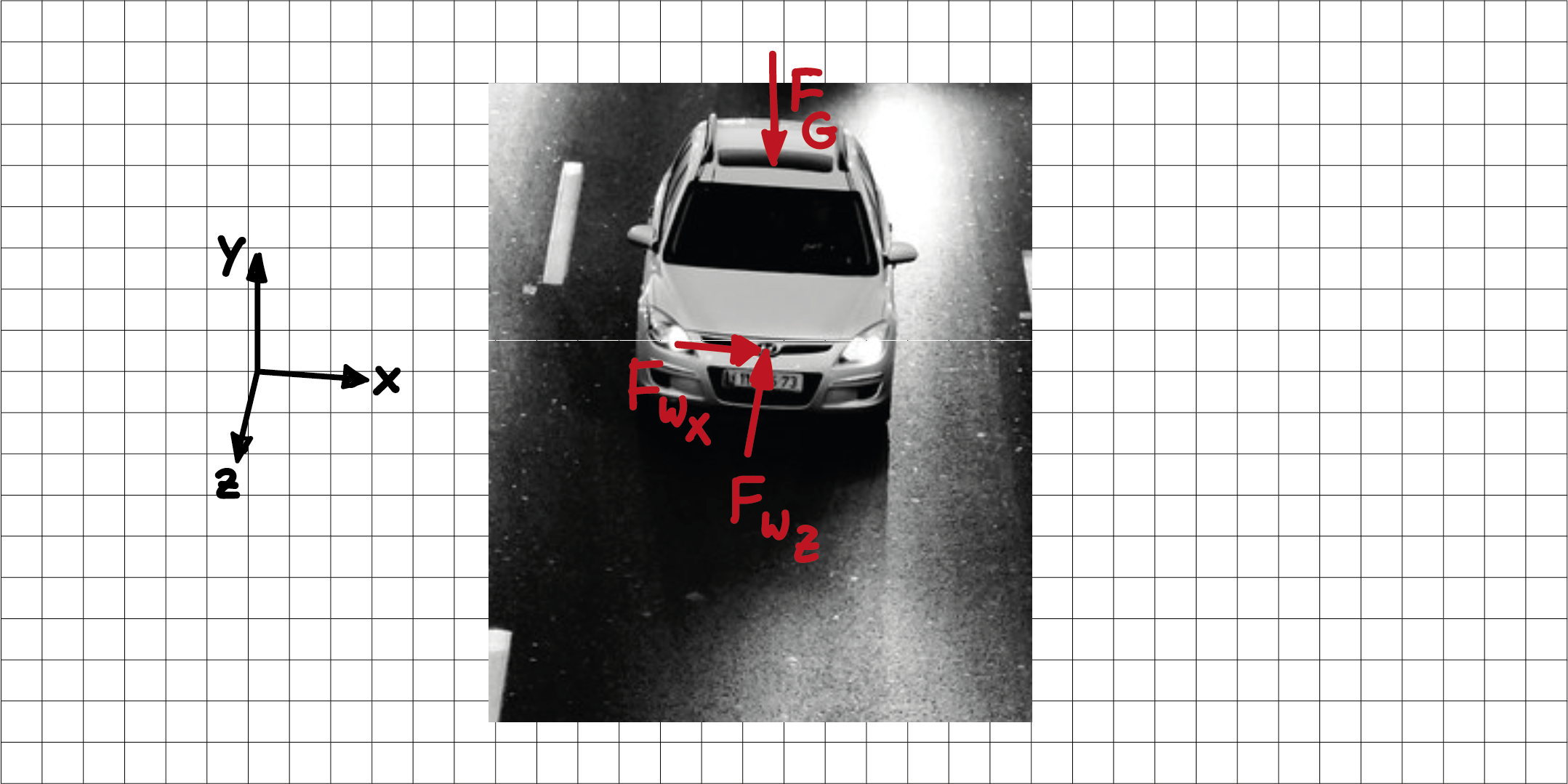
Räumliches Kräftesystem: Fahrzeug mit Belastungen durch Gewichtskraft und Wind
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg (Ausschnitt und handschriftliche Ergänzungen) auf Basis von RG in TLV
CC BY 2.0
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/Raeumliches_Kraeftesystem_Fahrzeug_mit_Windlast_und_Gewichtskraft.png
https://www.flickr.com/photos/30845197@N00/22028571392
Auch das, was wir über Momente für das ebene System festgestellt haben, lässt sich natürlich für das räumliche Kräftesystem übertragen und erweitern: Auch im räumlichen Kräftesystem treten natürlich Momentenwirkungen und Einzelmomente auf. Sie können Komponenten in alle Koordinatenrichtungen haben, da ja Kräftepaare mit Wirkungslinien in alle drei Achsrichtungen auftreten können.
Zusammenfassung - Das Wichtigste in Kürze
Kräftesysteme
Mit einem Kräftesystem sind alle auf einen Körper wirkenden Kräfte gemeint.
In einem ebenen Kräftesystem liegen die Wirkungslinien aller Kräfte in einer Ebene. Für die resultierenden Momente und die Einzelmomente bedeutet dies, dass sie ausschließlich um die Achse senkrecht zu dieser Ebene wirken.
Beispiel für ein ebenes System in der \( xy- \)Ebene:
Die Wirkunglinien aller Kräfte und ihre Ortsvektoren liegen in der \( xy- \)Ebene. Momente wirken nur um die \(z-\)Achse.
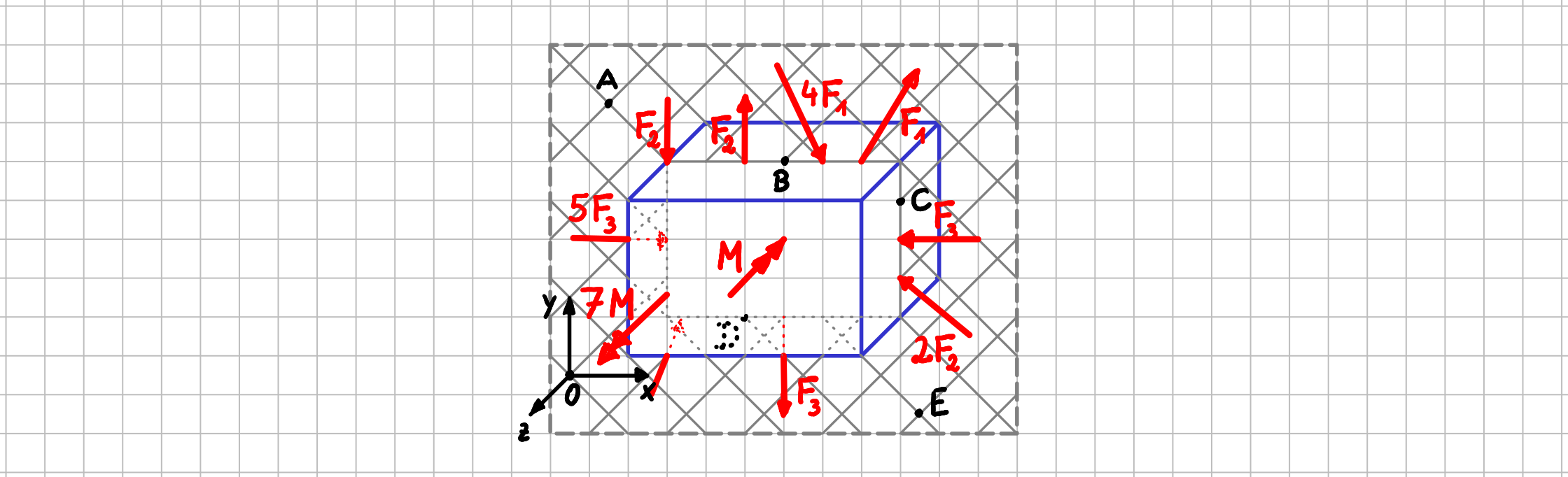
Ebenes Kräftesystem
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/Ebenes_Kraeftesystem_Zusammenfassung.png
In einem räumlichen Kräftesystem liegen Wirkungslinien und Ortsvektoren von Kräften nicht mehr alle in einer Ebene. Oft gibt es Kräfte mit Komponenten in alle drei Raumrichtungen. Momente oder Momentenkomponenten können daher auch um alle drei Achsen wirken.
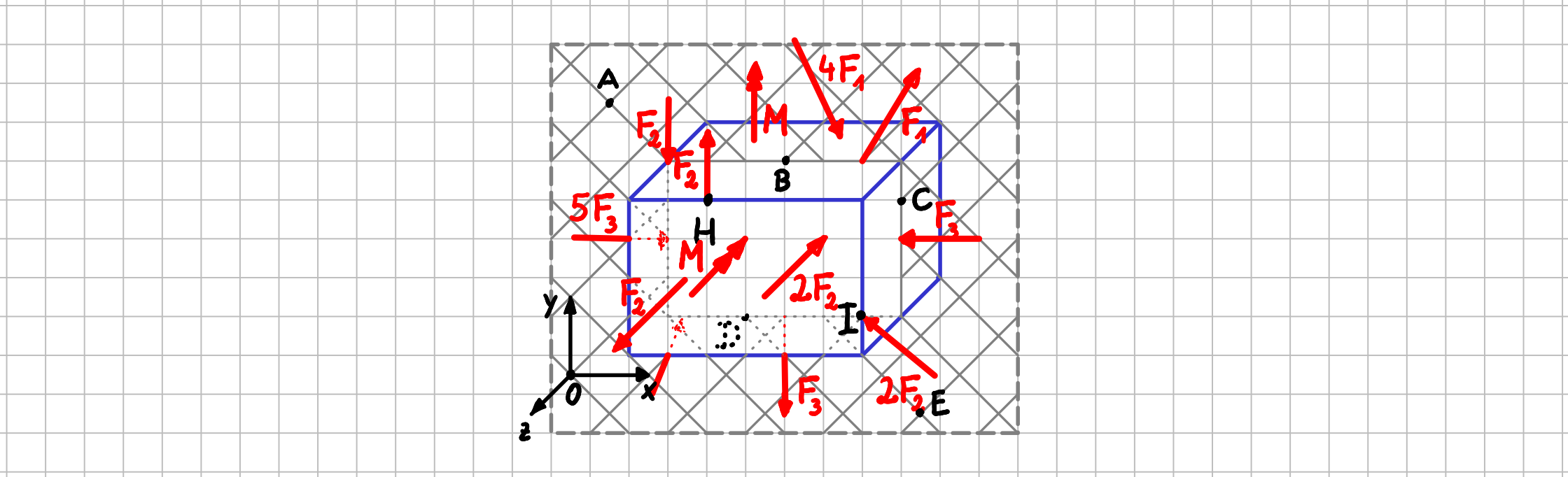
Räumliches Kräftesystem
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/raeumliches_Kraeftesystem_Zusammenfassung.png
2.3. Kräfte in der Realität vs. im Modell
Kräfte in der Realität vs. im Modell
Kräfte können zum Beispiel danach unterschieden werden, ob sie in der Natur vorkommen oder ob sie 'nur' in Modellen verwendet werden. Die Aufgabe von Ingenieuren ist es ja, mit Modellen und mathematischen Gleichungen reale Systeme und ihr Verhalten zu beschreiben. Dabei werden immer wieder Idealisierungen oder Vereinfachungen getroffen. Das mag jetzt auf den ersten Blick vielleicht negativ klingen. Aber so ist es nicht. Ganz im Gegenteil. Ingenieure sind clever und daher im positiven Sinne faul: Sie versuchen die Modelle immer nur so genau zu machen, wie es für den konkreten Anwendungsfall erforderlich ist.
In der linken Spalte der folgenden Abbildung sind daher die in der Natur vorkommenden Kräftearten dargestellt. In der rechten Spalte sind diejenigen Kräftearten zu sehen, die in Modellen verwendet werden. Auch wenn die Gewichtskraft eine über das Volumen eines Körpers verteilte Kraft ist, reicht es in vielen Fällen aus, sie als Einzelkraft im Schwerpunkt zu berücksichtigen.
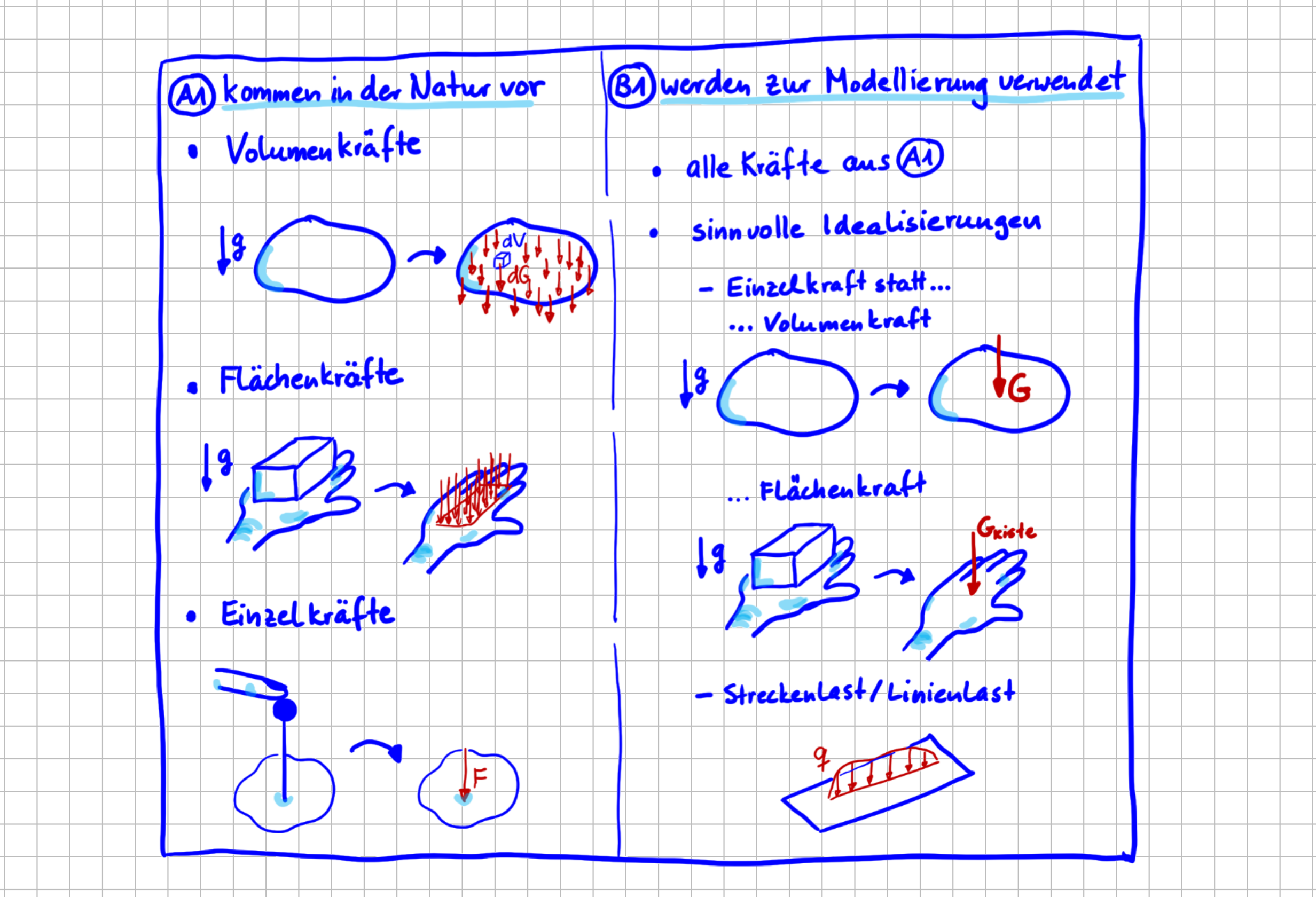
Abgrenzung von Kräften nach Vorkommen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2165/Abgrenzung_von_Kraeften_nach_Vorkommen.png
2.4. Zulässige Operationen
Zulässige Operationen bei Kräften
Es gibt gewisse Operationen, die du mit Kräften durchführen kannst, ohne dass sich die "Wirkung nach außen" ändert.
Bevor wir uns überlegen können, was überhaupt Operationen sind, die man mit Kräften durchführen kann, müssen wir uns erstmal anschauen, was mit "Wirkung nach außen" gemeint ist. Nur dann können wir verstehen, warum gewisse Operationen erlaubt sind und andere nicht.
Mit "Wirkung nach außen" ist gemeint, dass sich -obwohl man eine Operation mit einer Kraft ausführt- am Gesamtverhalten des Systems nichts ändert: Die Lagerreaktionen bleiben also gleich.
Wenn du ganz neu im Bereich Mechanik unterwegs bist, solltest du an dieser Stelle erst die Kapitel "Freischneiden & Actio=Reactio" sowie "Gleichgewichtsbedingungen" durcharbeiten, damit du alles im Folgenden verstehen kannst.
Oder du machst auch ohne Kenntnis dieser beiden Kapitel hier erst einmal weiter und kommst nachdem du die beiden Kapitel erarbeitet hast, ein zweites Mal hierher zurück.
Wenn du dich schon mal mi Gleichgewichtsbedingungen beschäftigt hast, sollten dir die folgenden Darstellungen hoffentlich schnell einleuchten.
Machen wir es konkret: Was kannst du mit der Kraft in den beiden folgenden Systemen 'anstellen', ohne dass sich die Lagerreaktionen (Beträge und Richtungen) verändern?

Ausgangssysteme mit Kräften
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Ausgangssysteme_mit_Kraeften.png
Wenn das Kriterium für erlaubte Kräfteoperationen ist, dass sich die Lagerreaktionen nicht ändern dürfen, müssen die Lagerreaktionen erstmal durch Freischneiden sichtbar gemacht werden. Das Ergebnis für die beiden Systeme sieht so aus:
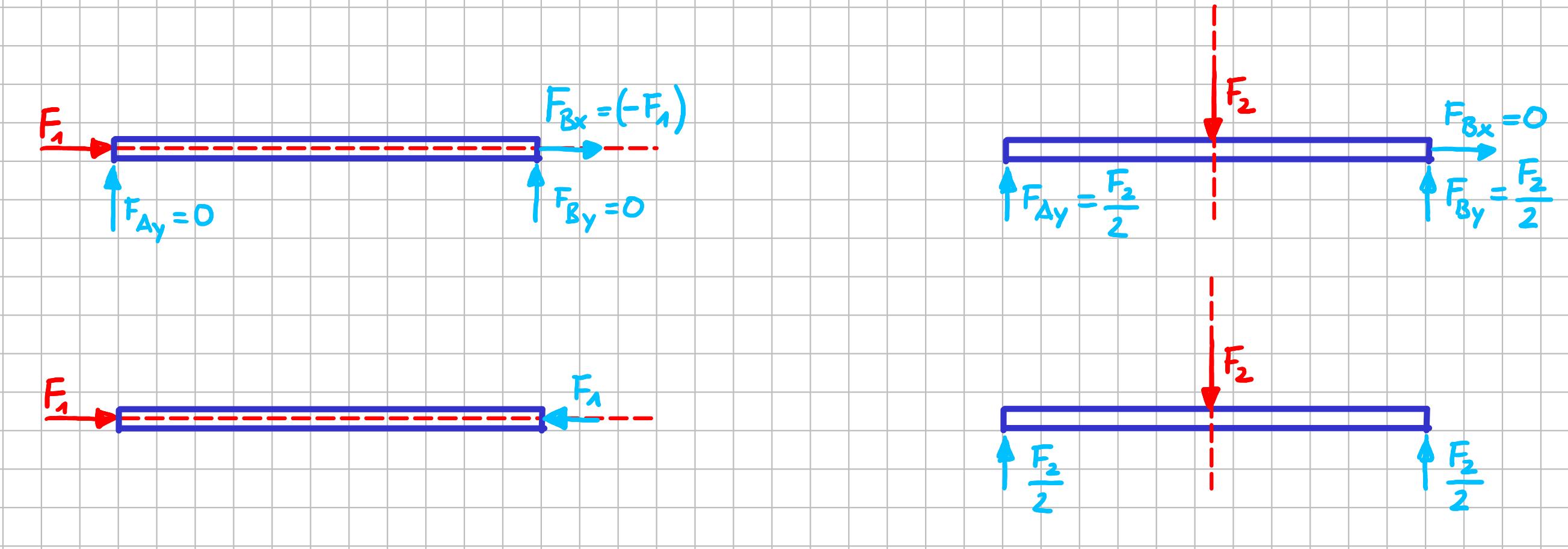
Freikörperbilder der Ausgangssysteme
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Freikoerperbilder_der_Ausgangssysteme.png
Damit leichter zu überblicken ist, welche Kräfte die ursprüngliche Belastung und welche die Lagerreaktionen sind, wurden die Lagerreaktionen ausnahmsweise in hellblau dargestellt.
Wenn die äußeren Kräfte \( F_1 \) und \( F_2 \) entlang ihrer Wirkungslinie verschoben werden, ändert das nichts an den Lagerreaktionen.

Kräfte verschoben entlang ihrer Wirkungslinien
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Kraefte_verschoeben_entlang_ihrer_Wirkungslinie.png
Verschieben einer Kraft entlang ihrer Wirkungslinie ist also eine zulässige Operation, da sich die Wirkung nach außen dadurch nicht ändert.
Und was ist mit dem Verschieben parallel zur Wirkungslinie? Das ist ja die logische nächste Frage. Schauen wir uns das anhand des rechten Systems einmal an. Wenn du beim rechten System die Kraft \( F_2 \) z.B. nach rechts verschieben würdest, dann sähe das so aus:

Kraft parallel verschoben zu ihrer Wirkungslinie
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Kraefte_parallel_verschoben_zu_ihrer_Wirkungslinie.png

Nullvektoren addieren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Nullvektoren_addieren.png
Für die praktische Anwendung ist diese Operation sicherlich nicht so relevant. Für die Betrachtungen im Zusammenhang mit der Momentwirkung von Kräften ist sie allerdings essentiell. Das wirst du im Kapitel Moment merken.
Bei der Betrachtung von mechanischen Systemen werden diese zwei zulässigen Operationen ständig verwendet: Das Addieren und Zerlegen von Kräften mit gemeinsamem Angriffspunkt.
Schauen wir uns zunächst das Addieren genauer an. Die folgenden drei Aussagen für die Kräfte \( \vec{F}_1 \), \( \vec{F}_2 \), die einen gemeinsamen Angriffspunkt haben, und ihre resultierende Kraft \( \vec{F}_{res} \) sind identisch:
- Die Kräfte \( \vec{F}_1 \) und \( \vec{F}_2 \) greifen an einem Punkt an. Ihre Wirkung ist identisch der Wirkung der resultierenden Kraft \( \vec{F}_{res} \), wenn \( \vec{F}_{res} \) aus der Parallelogramm-Konstruktion bestimmt wird.
- \( \vec{F}_1 + \vec{F}_2 = \vec{F}_{res} \)
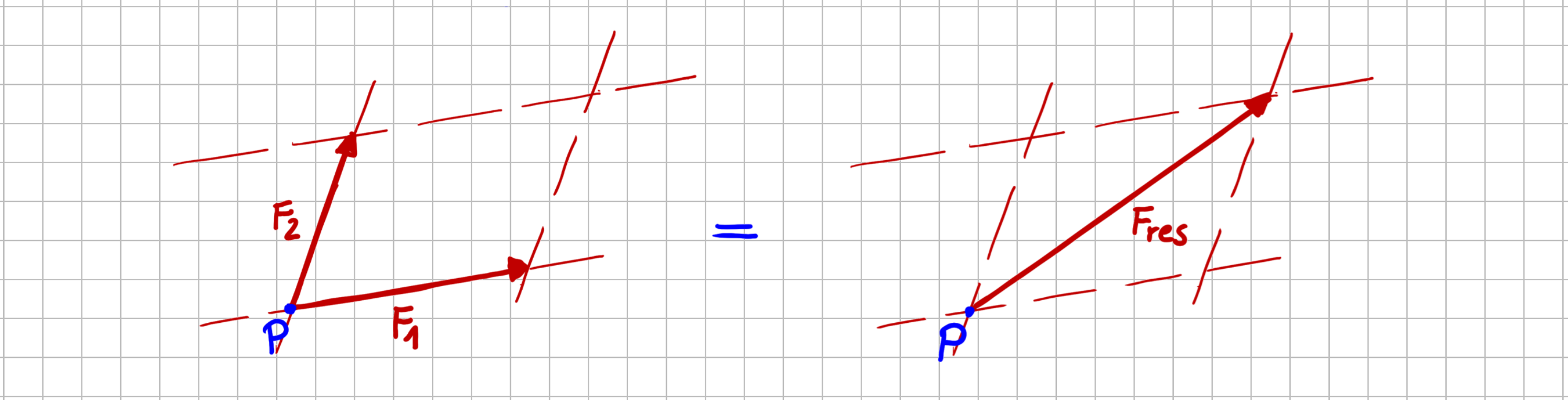
Addition von Kraftvektoren mit gemeinsamem Angriffspunkt: Konstruktion der resultierenden Kraft mittels Parallelogramm-Regel
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Addition_von_Kraftvektoren_mit_gemeinsamem_Angriffspunkt.png
Die Umkehrung gilt natürlich auch: eine Kraft kann in zwei Kräfte mit demselben Angriffspunkt zerlegt werden, wenn die Parallelogramm-Regel verwendet wird. Diese Form der Kraftzerlegung kennst du vielleicht schon aus einer ganz praktischen Anwendung: Wenn sich ein Fahrzeug festgefahren hat, kannst du es mit einem weiteren Fahrzeug, das die Kraft \( \vec{F} \) aufbringt, freischleppen. Oder du verwendest zwei Fahrzeuge oder auch Seilwinden, die die Kräfte \( \vec{F}_1 \) und \( \vec{F}_2 \) aufbringen und zwar so, das die resultierende Kraft \( \vec{F}_{res} \) wieder genau \( \vec{F} \) ist.
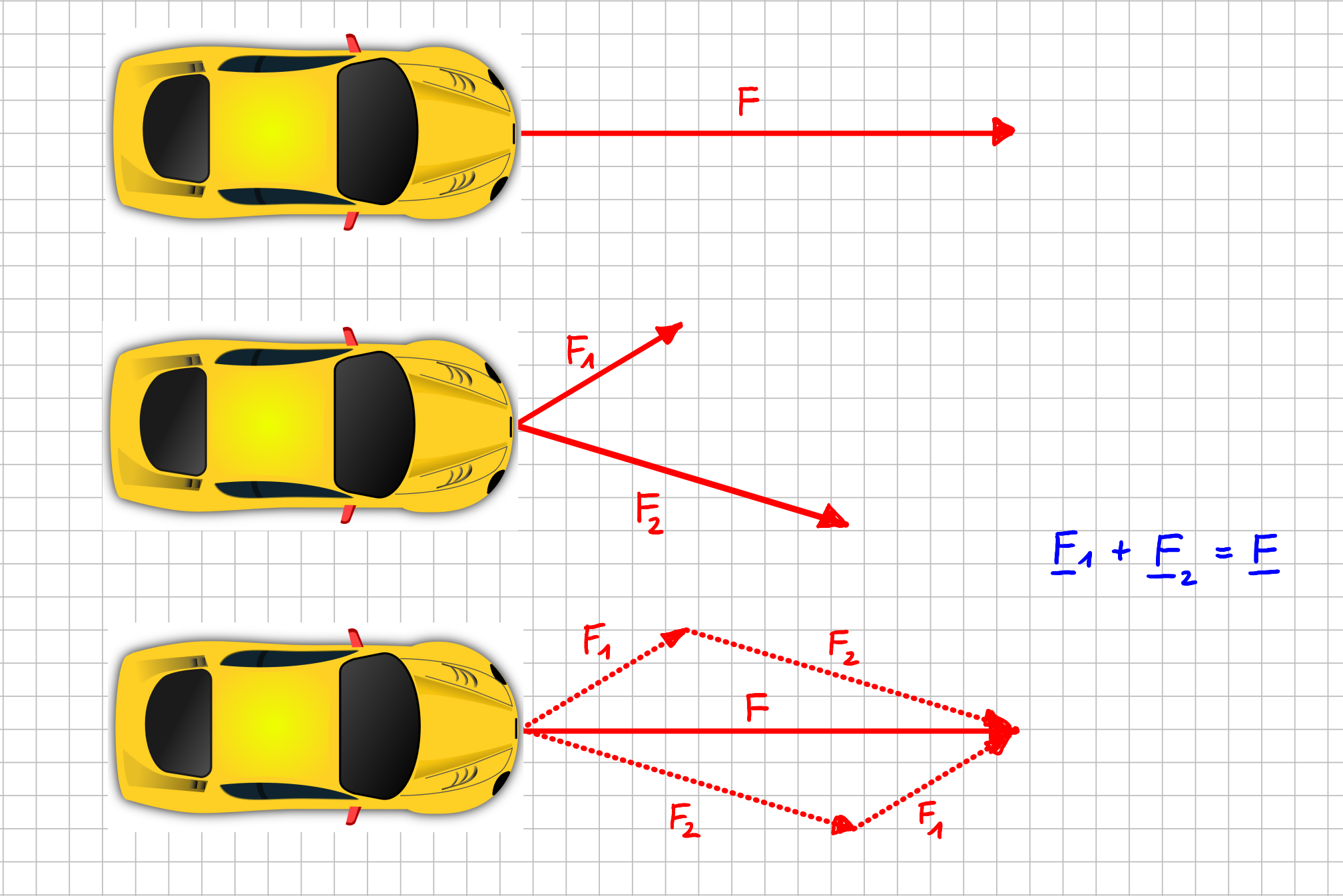
Anwenden der Kraftzerlegung beim Freischleppen eines Fahrzeugs
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg, auf der Basis von von Peeyush.ciit
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Anwenden_der_Kraftzerlegung_beim_Freischleppen_eines_Fahrzeugs.png https://upload.wikimedia.org/wikipedia/commons/c/cf/Travel-car-topview.svg
Bei der Betrachtung von mechanischen Systemen verwenden wir diese Zerlegung wirklich sehr oft. Meist werden Kräfte in ihre Komponenten bezüglich eines gegebenen Koordinatensystem zerlegt. Und da die Achsen dieses Koordinatensystems senkrecht zueinander stehen, sieht die Zerlegung dann so aus:
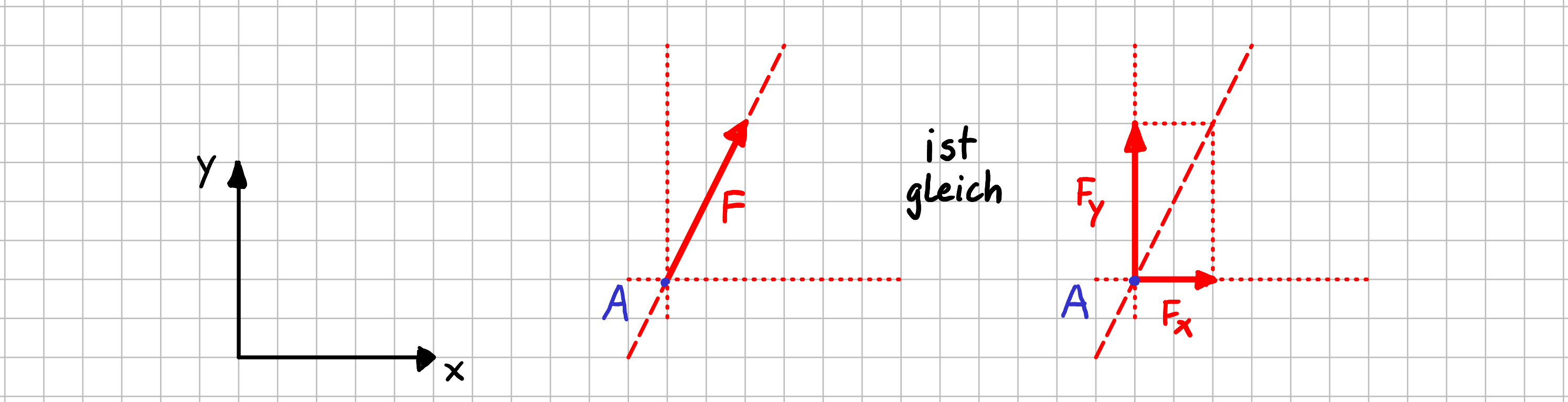
Zerlegung eines Vektors in seine Komponenten im karthesischen Koordinatensystem
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Zerlegung_eines_Vektors_in_seine_Komponenten.png
Zusammenfassung - Das Wichtigste in Kürze
Operationen mit Kräften, die die Wirkung nach außen nicht verändern
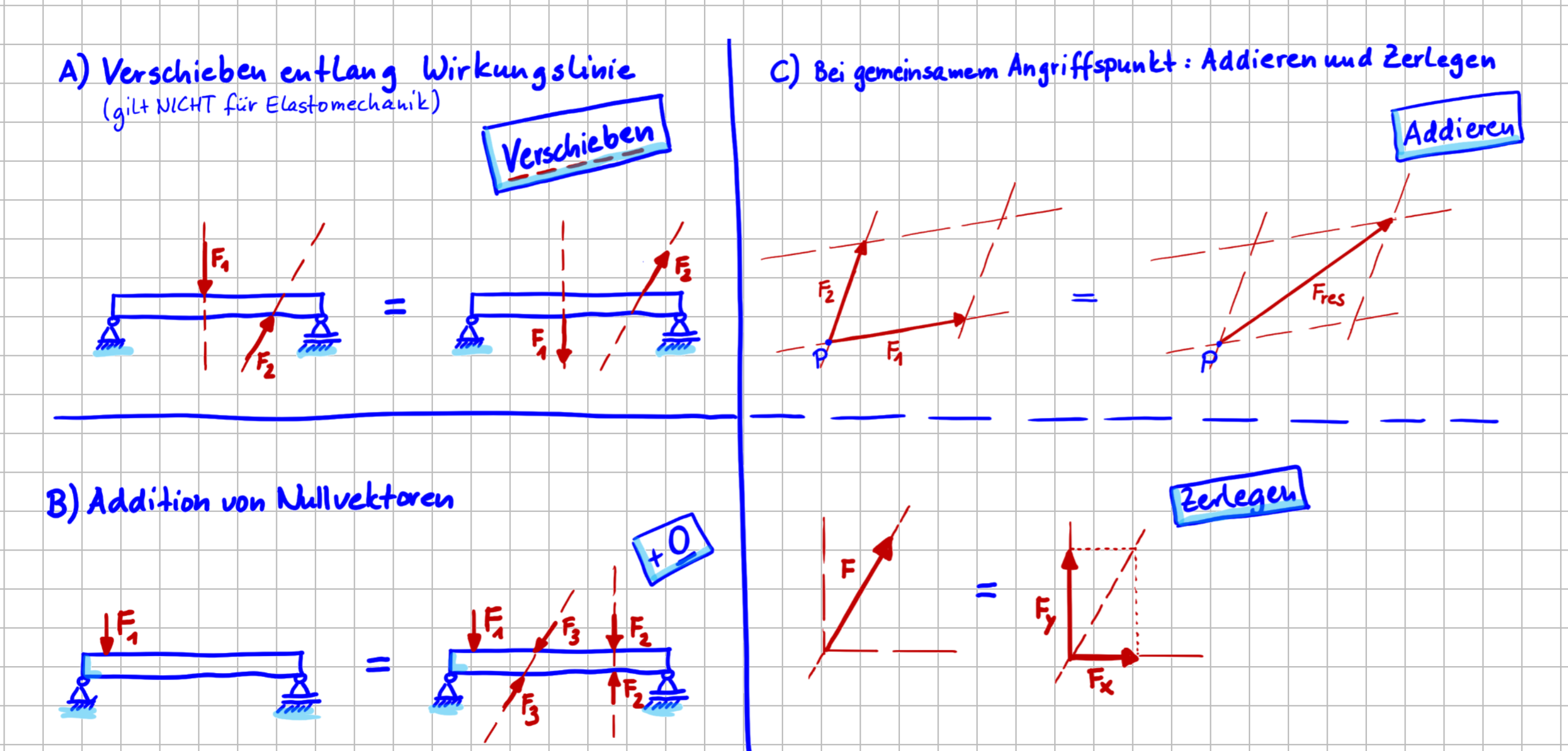
Zusammenstellung von Operationen mit Kräften ohne Veränderung der Wirkung nach außen
Weitere Informationen
Damit solltest du nun die wichtigsten Operationen, die mit Kräften erlaubt sind, kennen.
2.5. Kraftzerlegung
Kraftzerlegung
Wenn du Mechanikaufgaben lösen willst, wirst du immer wieder Kräfte in ihre Komponenten bezüglich der gegebenen Koordinatenachsen zerlegen. Weil es so oft vorkommt, solltest du dieses Vorgehen quasi im Schlaf beherrschen. Deswegen wollen wir uns in diesem Abschnitt genau anschauen, wie das eigentlich geht.
Was du an mathematischem Werkzeug mitbringen solltest: Sicher mit den Winkelfunktionen Sinus und Cosinus umgehen können. Schau gerne nochmal im Kapitel Tirgonometrie vorbei, wenn du das erst noch üben willst: Hier geht's zum Kapitel Trigonometrie.
In der folgenden Abbildung links siehst du einen Balken, der an der linken Seite fest eingespannt ist. Er ist im Punkt \(B\) mit der Kraft \(\vec{F}\) belastet. Die Kraft greift unter dem Winkel \(\delta\) zur Horizontalen an. Auf der rechten Seite ist die Kraft \(\vec{F}\) in ihre Komponenten zerlegt worden.
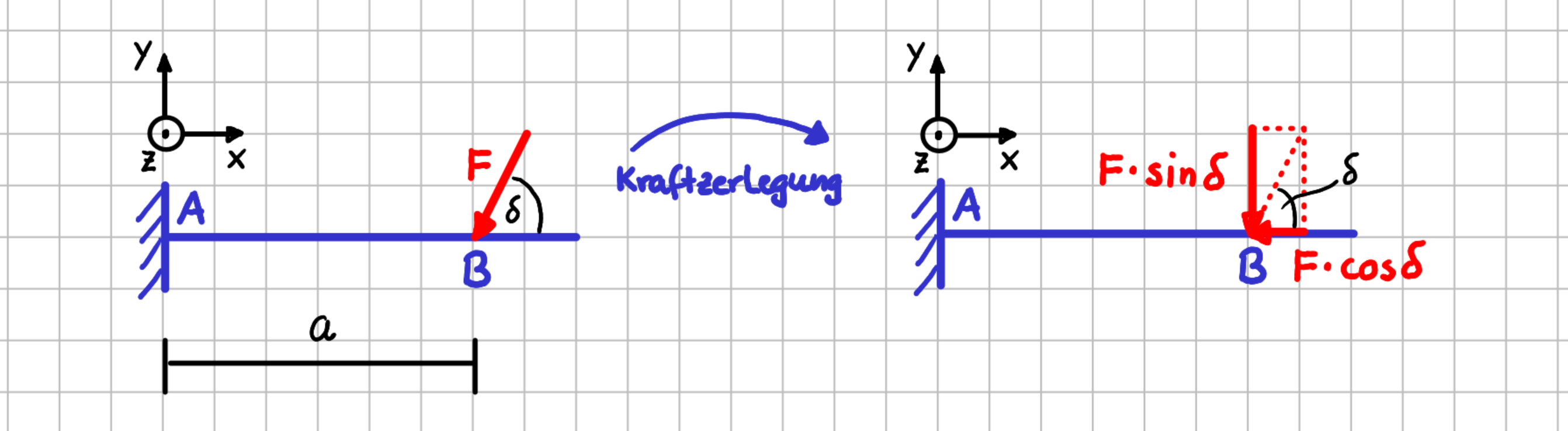
Kraftzerlegung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2173/Kraftzerlegung.png
Warum muss die Kraft jetzt überhaupt zerlegt werden?
Wenn du die Lagerkräfte für dieses System berechnen willst, musst du nach dem Erstellen des Freikörperbildes unter anderem das Kräftegleichgewicht aufstellen. Dazu muss du wissen, wie groß die die Anteile von \(\vec{F}\) in die \(x-\) und \(y-\) Richtung sind.
Wie das mit der Kraftzerlegung genau geht, siehst du in der folgenden Abbildung. Es sind vier Schritte, die du durchläufst. Ich empfehle dir, am Anfang die Schritte wirklich so ausführlich hinzuschreiben bzw. hinzuzeichnen, wie ich es getan habe. Später wirst du das vermutlich alles im Kopf machen.
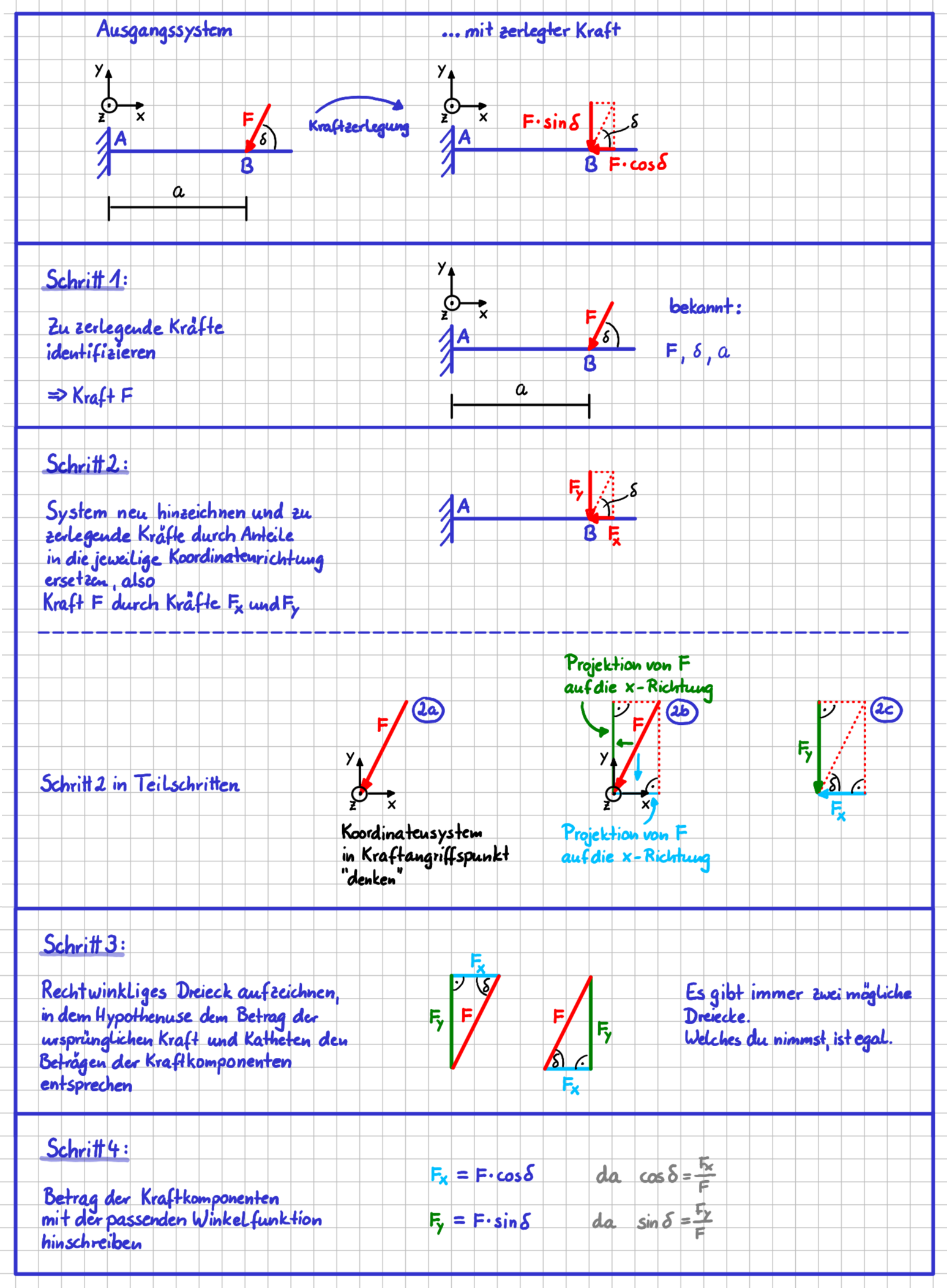
Kraftzerlegung Schritt für Schritt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2173/Kraftzerlegung_Schritt_fuer_Schritt%20%281%29.png
Worauf kommt es an? Ganz wichtig ist, dass du dir klarmachst, dass du in Schritt 2 eine Vektoroperation an einem Kraftvektor, also einem gebundenen Vektor durchführst. Diese Zerlegung musst du im Angriffspunkt der Kraft durchführen. Das bedeutet, dass die beiden Kraftkomponenten, die du durch die Zerlegung bekommst, mit ihren Pfeilspitzen auf den Kraftangriffspunkt zeigen.
In Schritt 3 führst du keine Vektoroperation, sondern eine rein geometrische Betrachtung durch, um die Beträge der beiden Vektorkomponenten zu bestimmen. Hier schaust du dir also reine Streckenlängen an. Du wählst dabei eines der beiden sich ergebenden rechtwinkligen Dreiecke aus. Der Betrag der ursprünglichen Kraft ist die Hypothenuse in diesen Dreiecken. Die Beträge der Komponenten entsprechen den Längen der Katheten.
Schritt 4 ist ein rein mathematischer Schritt, in dem du die trigonometrischen Beziehungen beim rechtwinkligen Dreieck verwendest, um die Länge der beiden Katheten in Abhängigkeit von gegebenem Winkel und Hypothenuse anzugeben.
Wenn du dich jetzt fragst: "Und was mache ich, wenn der Kraftangriffspunkt nicht auf dem Bauteil liegt?", dann ist das eine berechtigte Frage. Du hast ja im vorangegangenen Abschnitt gerade gesehen, dass es gewisse Operationen bei gebundenen Vektoren wie Kräften gibt, die du durchführen darfst, ohne dass sich die Wirkung nach Außen ändert.
Schauen wir uns das anhand des folgenden Beispiels mal genauer an.
xxx BILD 1
Du kannst eine Kraft ja entlang ihrer Wirkungslinie verschieben. Wenn du das tust, so dass der Kraftangriffspunkt auf dem Bauteil liegt, sieht die Kraftzerlegung auch nicht mehr "komisch" aus.
Aufgabe - Jetzt bist du dran
2.6. Eingeprägte vs. Reaktionskraft
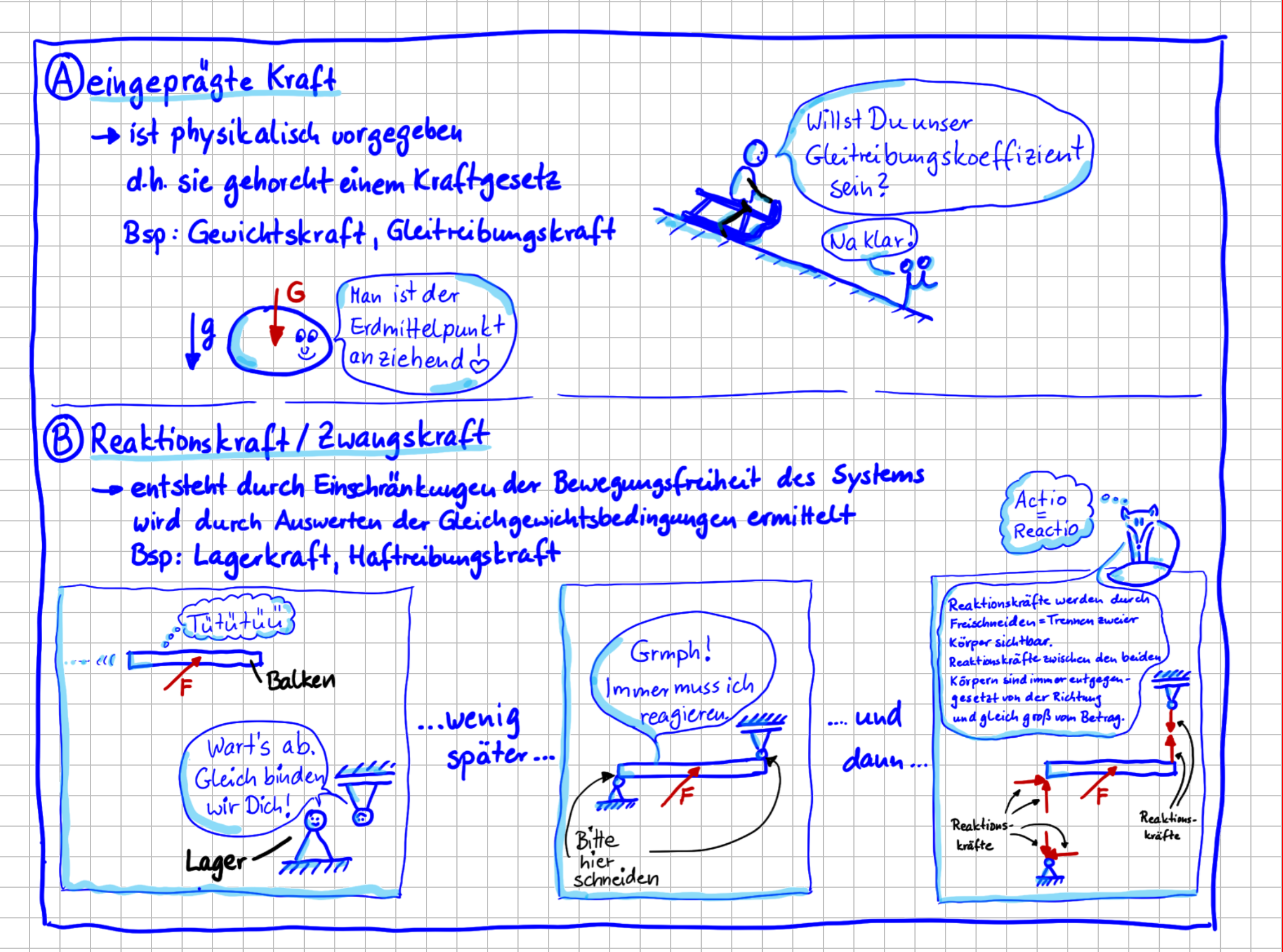
Eingeprägte vs. Reaktionskraft
Kräfte können auch danach unterschieden werden, ob sie zur Gruppe der "eingeprägten Kräfte" oder zur Gruppe der "Reaktionskräfte" gehören.
Bei eingeprägten Kräften ist der Bestimmtheitsgrad von vornherein größer. Ich erkläre dir, was damit gemeint ist.
Erinnern wir uns nochmal daran, was es braucht, um eine Kraft (= gebundener Vektor) eindeutig zu beschreiben:
- die Richtung
- die Lage des Angriffspunktes bzw. der Wirkungslinie
- den Betrag
Bei einer eingeprägten Kraft sind diese drei Eigenschaften 'von vorneherein' bekannt, da eingeprägte Kräfte einem Kraftgesetz gehorchen.
Schauen wir uns das am Beispiel der Gewichtskraft an.
Hier ist das Kraftgesetz das Gravitationsgesetz. Wir wissen also von vornherein, dass die Richtung (1.) der Gewichtskraft in Richtung des Erdmittelpunktes zeigt, also in Richtung des Erdbeschleunigungsvektors \(\vec{g}\) . Außerdem wissen wir, dass der Angriffspunkt (2.) der Schwerpunkt des Körpers ist. Auf der Erdoberfläche ist der Betrag (3.) der Gewichtskraft eines Körpers gleich seiner Masse mal der Erdbeschleunigung: \(\vec{G}=m \cdot \vec{g} \) . Alle drei Merkmale sind also von vorneherein bekannt. Es braucht nicht erst ein System und irgendwelche Berechnungen am System.
Wie sieht das jetzt konkret aus, wenn z.B. die statische Belastung der Lager für ein Feuerwehrfahrzeug bestimmt werden soll?
Wie wir gerade festgestellt haben, sind für die Gewichtskraft \( \vec{G} \) alle drei benötigten Informationen bekannt. Die eingeprägte Kraft lässt sich also direkt im Freikörperbild einzeichnen.
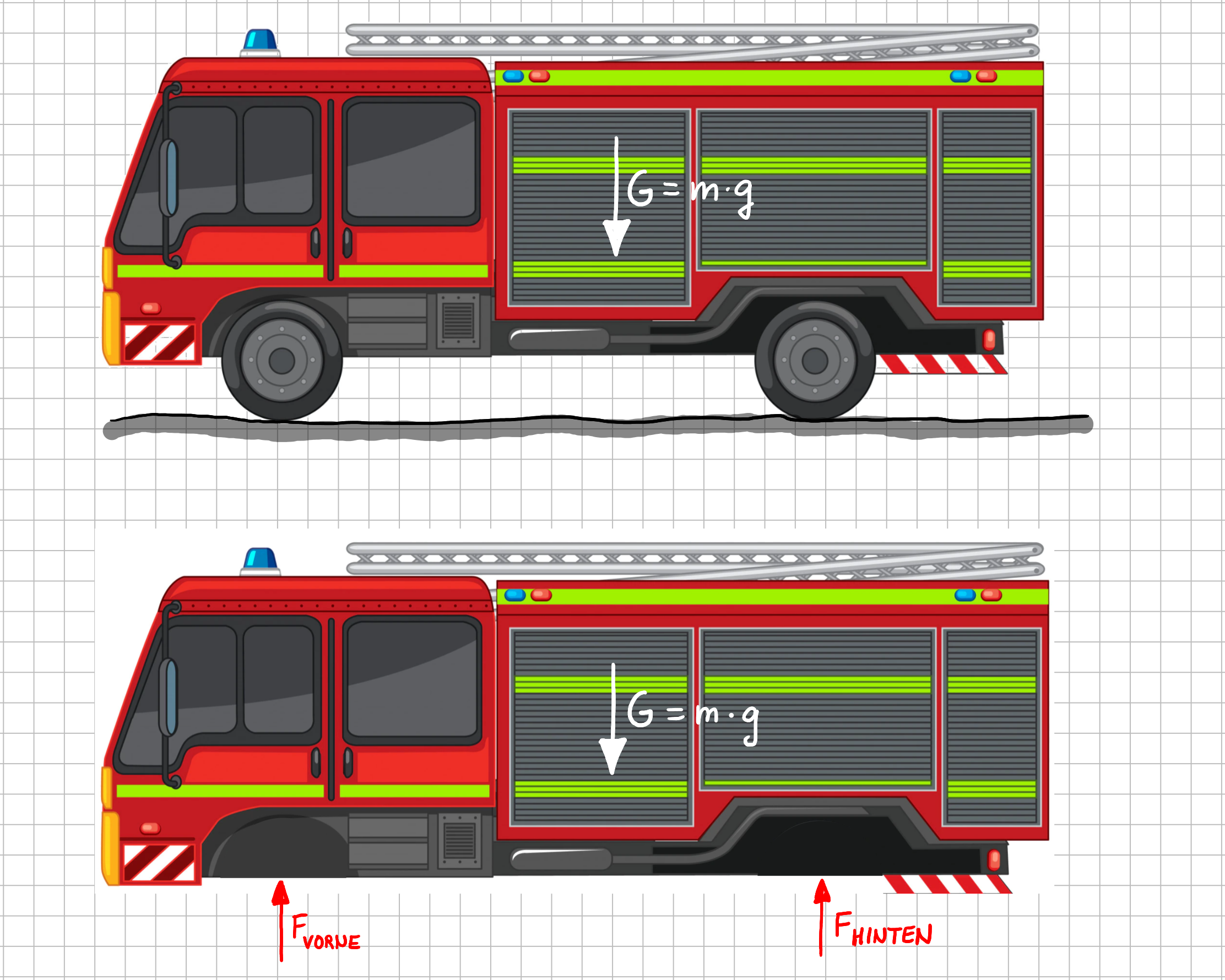
Veranschaulichung des Unterschieds zwischen eingeprägter und Reaktionskraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg, auf Basis von brgfx (freepic)
CC BY-SA 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2162/Veranschaulichung_des_Unterschieds_zwischen_eingepr%C3%A4gter_und_Reaktionskraft.png
https://de.freepik.com/vektoren-kostenlos/feuerwehrauto-auf-weiss_5936246.htm
Abgrenzung von Kräften nach Bestimmtheitsgrad
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2162/Abgrenzung_von_Kr%C3%A4ften_nach_Bestimmtheitsgrad.png
Wie deutlich wird, ist die Reibkraft eine Kraft, die sowohl eingeprägte Kraft (Gleitreibungskraft) als auch Reaktionskraft (Haftreibungskraft) ist. Das ist natürlich besonders spannend. Diesem Punkt widmen wir uns beim Thema Reibung im Detail.
Zusammenfassung - Das Wichtigste in Kürze
Um einen Kraftvektor eindeutig zu beschreiben, müssen die drei folgenden Informationen bekannt sein:
- die Richtung
- den Angriffspunkt bzw. die Lage der Wirkungslinie
- den Betrag
Beispiele: Gewichtskraft, Federkraft, Dämpferkraft, Gleitreibungskraft
3. Verschiedene Kraftarten ganz nah
Verschiedene Kraftarten ganz nah
Einige Arten von Kräften tauchen immer wieder auf. Deswegen lohnt es sich, diese Kraftarten noch einmal ganz aus der Nähe zu betrachten. In diesem Abschnitt geht es daher auf Tuchfühlung mit einzelnen Kräften.

Verschiedene Kraftarten in Alltagssituationen
Weitere Informationen
upklyak, freepik, brgfx, fabrikasimf
Freepik License
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2172/unterschiedliche_Kraftarten_im_Alltag.png
3.1. Gewichtskraft
Alle Körper ziehen sich aufgrund ihrer Masse gegenseitig an. Die wirkenden Kräfte bezeichnet man als Gravitationskraft. Das hat Isaac Newton schon im 17. Jahrhundert festgestellt.
Schauen wir uns das einmal genauer für zwei beliebige Körper \(1\) und \(2\) mit den Massen \(m_1\) und \(m_2\) an. Die Gravitationskräfte wirken entlang der Verbindungslinie der Schwerpunkte, sind entgegengesetzt gerichtet und vom Betrag her gleich groß.
Wenn \(r\) der Abstand zwischen den beiden Schwerpunkten ist, lässt sich die Gravitationskraft \(F_G\) so berechnen:
$$F_G=G \cdot \dfrac{m_1 \cdot m_2}{r^2}.$$
Der Faktor \(G\) ist eine universelle Konstante. Sie hat den Wert
$$G=6,673\cdot 10^{-11}\dfrac{\mathrm{m}^3}{\mathrm{kg} \cdot \mathrm{s}^2}.$$
Die Gravitationskraft ist also direkt proportional zum Produkt der beiden Massen und umgekehrt proportional zum Quadrat des Abstandes zwischen den beiden Massen.
Aufgrund der Gravitationskraft bleiben wir überhaupt auf der Erdoberfläche und fliegen nicht durch den Weltraum.
Lass uns als Körper \(1\) die Erde nehmen und als Körper \(2\) irgendein Objekt auf der Erde. Dann gilt \(m_1=m_{\mathrm{Erde}}=5,972 \cdot 10^{24} \mathrm{kg}\). Da der Erdradius im Verhältnis zur Größe irgendeines Körpers auf der Erdoberfläche groß ist, können wir für den Abstand \(r\) zwischen dem Schwerpunkt der Erde und dem Schwerpunkt des Objektes auf der Erde in guter Näherung den mittleren Radius der Erde verwenden: \(r=r_{\mathrm{Erde}}=6371\mathrm{km}\). Dann sieht die Formel so aus:
$$F_G=G \cdot \dfrac{m_{\mathrm{Erde}} \cdot m_2}{r_{\mathrm{Erde}}^2} = g \cdot m_2.$$
Da bis auf \(m_2\) alle Faktoren konstant und bekannt sind, können wir diese zu einer neuen Konstante \(g=G \cdot \dfrac{m_{\mathrm{Erde}}}{r_{\mathrm{Erde}}^2}\) zusammenfassen. Für die Größe \(g\) ergibt sich dann die Einheit \(\dfrac{m}{s^2}\), also die Einheit einer Beschleunigung. Da wir uns auf der Erdoberflcähe befinden, wird \(g\) als Erdbeschleunigung oder auch Erdbeschleunigungskonstante bezeichnet. Wenn du die Zahlenwerte der drei Konstanten einsetzt, kannst du den Wert für die Erdbeschleunigung \(g\) ausrechnen: \(g=9,81 \dfrac{m}{s^2}.\) Wenn du bei Berechnungen keinen Taschenrechner hast oder benutzen darfst, kannst du in guter Näherung auch \(g=10 \dfrac{m}{s^2}\) verwenden.
Auf der Erdoberfläche gilt dann also für die Gravtitationskraft einer Masse \(m\):
$$F_G = m \cdot g.$$
Die Gravitationskraft wird auch als Gewichtskraft oder Gewicht bezeichnet.
In der Umgangssprache werden die Begriffe 'Masse' und 'Gewicht' leider oft gleichwertig verwendet. Überleg mal selbst, ob du schon mal "Meine Masse ist 65kg." gesagt hast, oder ob du "Mein Gewicht ist 65kg." sagst.
In der Mechanik ist es eindeutig:
Gravitationskraft = Gewichtskraft = Gewicht ist ein Kraft, hat also die Einheit Newton.
Die Masse ist die Größe, die die Einheit Kilogramm hat.
Pass da also gut auf und lass dich nicht durch den "schlampigen" Umgang mit Begriffen in der Umgangssprache verwirren.
Welche Einheit hat denn die Gewichtskraft nun eigentlich?
$$F_G = m \cdot g $$
also
$$[\mathrm{Einheit} \mathrm{Gewichtskraft}]= \mathrm{kg} \cdot \dfrac{\mathrm{m}}{\mathrm{s^2}} $$.
Die Einheiten, die auf der rechten Seite stehen \(-\) Kilogramm, Meter, Sekunde \(-\) sind alle Standardeinheiten. Da die Einheit einer Kraft immer wieder vorkommt, hat man die Einheitenkombination \( \mathrm{kg} \cdot \dfrac{\mathrm{m}}{\mathrm{s^2}} \) zu Ehren Isaac Newtons \(\mathrm{Newton}\) genannt, was mit einem großen N, also \(\mathrm{N}\) angegeben wird:
$$1 \mathrm{N} = 1 \mathrm{kg} \cdot \dfrac{\mathrm{m}}{\mathrm{s^2}}.$$
Zusammenfassung - Das Wichtigste in Kürze
In der Mechanik werden die Begriffe "Gravitationskraft", "Gewichtskraft" und "Gewicht" gleichwertig verwendet. Die Gewichtskraft bezeichnet die Kraft, die auf einen Körper auf der Erdoberfläche aufgrund der wechselseitigen Anziehung mit der Erde wirkt.
Für die Gewichtskraft \(F_G\) eines Körpers mit der Masse \(m\) gilt mit der Erdbeschleunigung \(g\) :
\(F_G = m \cdot g \) .
Für die Einheiten gilt
\([\mathrm{Einheit} \mathrm{Gewichtskraft}]= [\mathrm{Einheit} \mathrm{Masse}] \cdot [\mathrm{Einheit} \mathrm{Erdbeschleunigung}]= \mathrm{kg} \cdot \dfrac{\mathrm{m}}{\mathrm{s^2}} .\)
Zu Ehren Isaac Newtons werden Kräfte in der Einheit \(\mathrm{Newton}\) angegeben und es gilt:
\(1 \mathrm{N} = 1 \mathrm{kg} \cdot \dfrac{\mathrm{m}}{\mathrm{s^2}}.\)
Die Gewichtskraft \(F_G\) zeigt in Richtung des Erdmittelpunktes und greift im Schwerpunkt des Körpers an. Sie ist vom Typ "Eingeprägte Kraft", da das Kraftgesetz \(F_G = m \cdot g \) gilt.
Die Erdbeschleunigung \(g\) hat den Wert \(g=9,81 \dfrac{m}{s^2}\). Für Überschlagsrechnungen kannst du in guter Näherung \(g=10 \dfrac{m}{s^2}\) verwenden.
Aufgabe - Jetzt bist du dran
3.2. Streckenlast = Linienlast
Streckenlast = Linienlast
Eine Streckenlast, die auch als Linienkraft bezeichnet
wird, ist zwar eine Idealisierung, die in realen Systemen kaum
vorkommt. Bei der Modellierung von räumlichen Systemen als ebene Systeme
ist sie aber eine sehr häufig verwendete Lastart. Sie wird z.B. dafür
verwendet, um das Eigengewicht von Komponenten mit seiner Verteilung zu
berücksichtigen. Das Eigengewicht ist ja in ganz vielen Anwendungen relevant, wie zum Beispiel bei Brücken und bei Dächern. Auch um flächige Lasten aus der Realität, wie z.B. Schneelasten, Windlasten, oder Auftriebslasten in zweidimensionalen Modellen zu berücksichtigen, kannst du die Streckenlast sehr gut verwenden. Es lohnt sich also, sich mit dieser Art von Belastung intensiver zu beschäftigen.
Aber der Reihe nach. Stell dir vor, du schneidest mit einem Messer z.B. Käse.
Wenn wir die Dicke der Schneide vernachlässigen, was sicherlich eine sehr plausible Näherung ist, dann ist die vom Messer auf den Käse wirkende Belastung eine Streckenlast.
Die Einheit ist "Kraft pro Länge" also z.B. \( \mathbf{\left[\frac{N}{m}\right]}. \)
Es ist also eine spezifische Größe, da sie auf die Länge bezogen ist.

Kraft zwischen der Schneide eines Messers und Käse als reales Beispiel für eine Streckenlast
Weitere Informationen
Charles Williams
CC BY 2.0
https://www.flickr.com/photos/99652207@N00/378503271
Für die mechanische und mathematische Darstellung werden üblicherweise folgende Bezeichnungen und Darstellungen verwendet:

Typische Bezeichnungen und Darstellungen im Zusammenhang mit Streckenlasten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Typische_Bezeichnungen_und_Darstellungen_Streckenlast.png
Schauen wir uns die Sache mit dem Eigengewicht eines Körpers, das über eine Streckenlast berücksichtigt werden kann, gleich mal genauer an.
Ein I-Träger, wie er auf dem Bild links zu sehen ist, wird in vielen bautechnischen Konstruktionen verwendet, z.B. in der Tragstruktur für eine Fabrikhalle.

I-Träger (links) und Verwendung in der Tragstruktur einer Fabrikhalle (rechts)
Weitere Informationen
Wir betrachten einen I-Träger mit den äußeren Abmessungen 200mm x 200mm aus Stahl und einer Stegbreite von 15mm bzw. 9mm. Er hat eine Masse von 63kg pro Meter Länge und damit eine Gewichtskraft von ca. 600N pro Meter.

Abmessungen und Gewichtskraft I-Träger
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Abmessungen_und_Gewichtskraft_I_Traeger.png
Wie wirkt es sich nun aus, wenn wir das Eigengewicht so eines Balkens in Form von Einzelkräften im Vergleich zu einer Streckenlast im Modell berücksichtigen? Dazu wollen wir uns ein Modell anschauen, bei dem ein Balken von 1m Länge am linken Ende mit einem Festlager und am rechten Ende mit einem Loslager gegenüber der Umgebung abgestützt ist.
Dieser Aufbau kann ein einem ebenen System abgebildet werden, da das Eigengewicht nur in einer Richtung wirkt, es also keinen räumlichen Belastungsfall gibt.
Das ebene System sieht dann so aus:
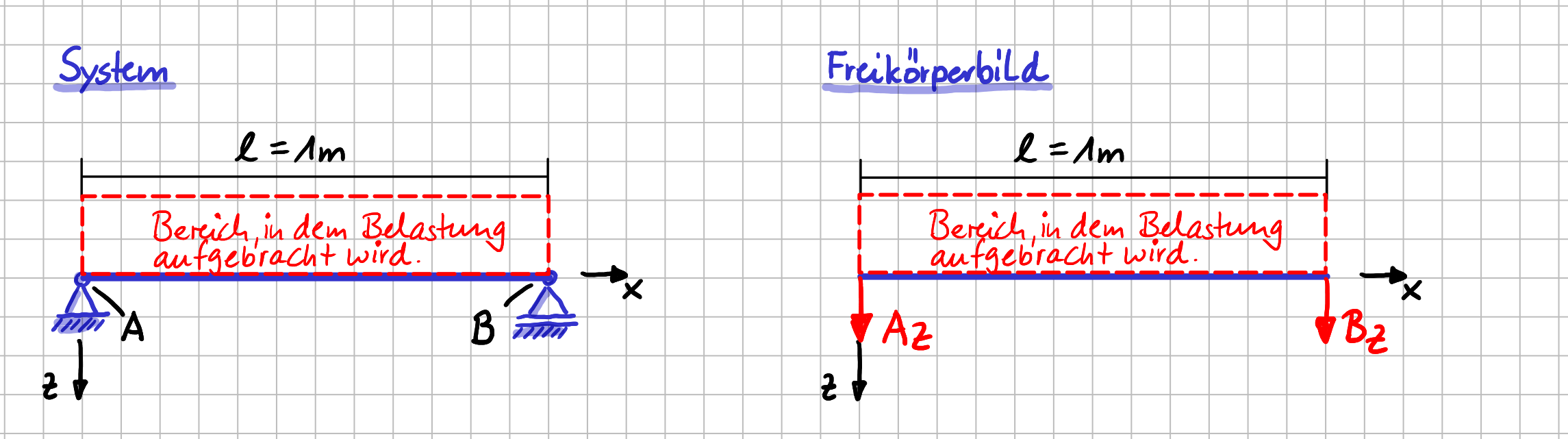
Ebenes Modell des Balkens mit Lagerung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Ebenes_Modell_des_Balkens_mit_Lagerung.png
Um das Eigengewicht von 600N zu berücksichtigen, hast du verschiedene Möglichkeiten. Du kannst eine Einzelkraft \( \vec{F}_1 \) mit einem Betrag von 600N aufbringen, Fall 1. Du kannst zwei Einzelkräfte \( \vec{F}_2 \) mit einem Betrag von je 300 N aufbringen, Fall 2. Du kannst drei Einzelkräfte mit einem Betrag von je 200 N aufbringen, Fall 3..... und so weiter. Oder du kannst eine konstante Streckenlast von 600\( \frac{\mathrm{N}}{\mathrm{m}} \) aufbringen, Fall 6.
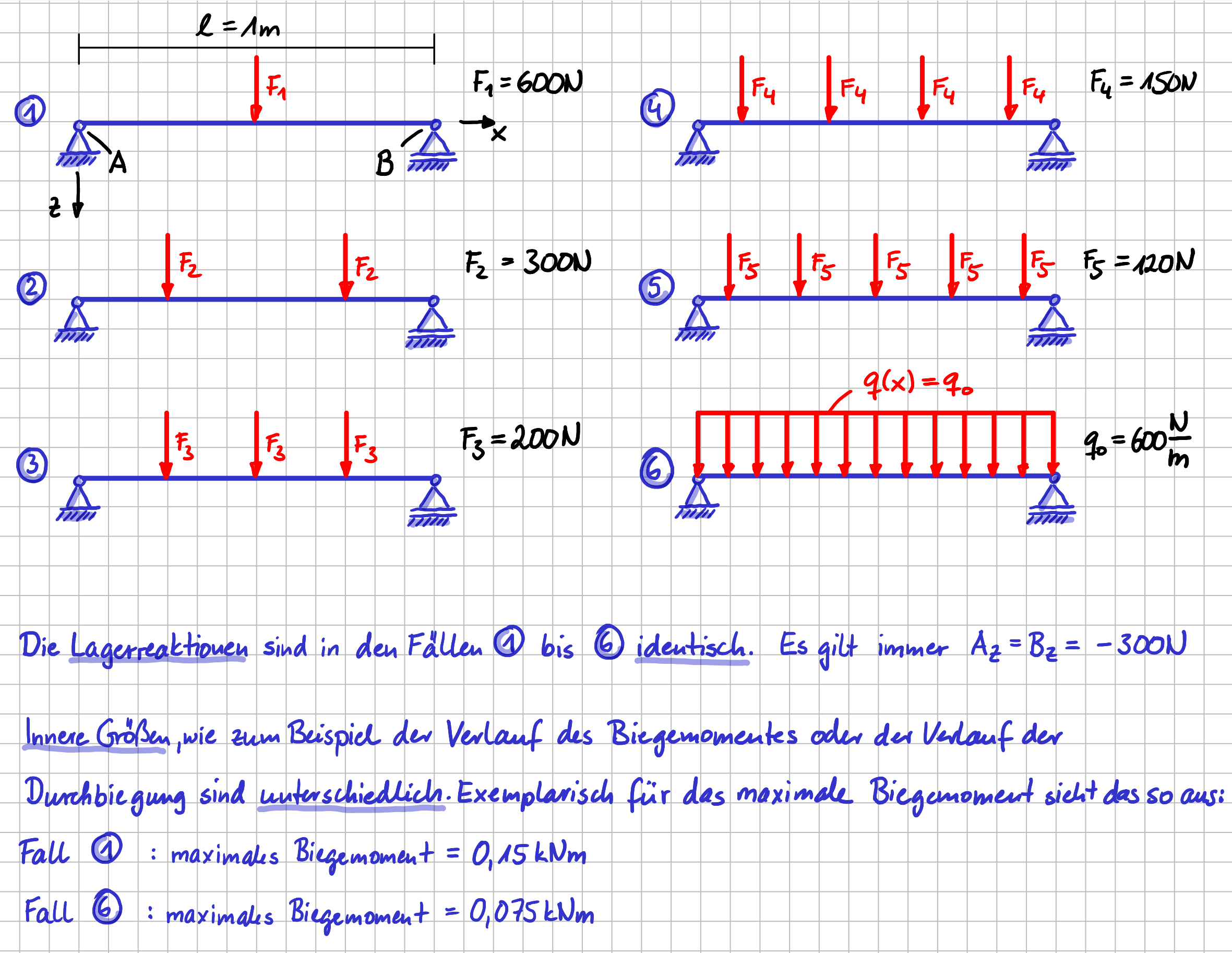
Verschiedenen Variante, um das Eigengewicht im Modell zu berücksichtigen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
Verschiedene_Varianten_um_Eigengewicht_im_Modell_zu_ber%C3%BCcksichtigen.png
Die Entscheidung darüber, wie genau du das Eigengewicht in deinem Modell berücksichtigen musst, hängt davon ab, was du untersuchen und berechnen willst. Die Werte der Lagerreaktionen \( A_z \) und \( B_z \) sind in allen sechs Fällen identisch. Bis du also nur an den Lagerreaktionen interessiert, reicht es aus, das Eigengewicht als Einzelkraft mit dem der Streckenlast entsprechenden resultierenden Größe zu berücksichtigen. Oder anders formuliert: Eine Streckenlast kann für die Berechnung der Lagerreaktionen zu einer äquivalenten Einzelkraft zusammengefasst werden.
Sobald du an inneren Größen interessiert bist, also z.B. wissen möchtest, wie stark sich der Balken durchbiegt oder wie groß das maximale Biegemoment ist, das im Balken auftritt, wird deine Berechnung umso genauer, je genauer du die Realität in deinem Modell abbildest. Und da das Eigengewicht des Balkens über seine gesamte Länge verteilt ist, bekommst du das genaueste Ergebnis für den Wert des maximalen Biegemoments, wenn du das Eigengewicht als Streckenlast berücksichtigst.
Wenn du dich mit mechanischen Systemen beschäftigst, wirst du immer wieder Streckenlasten \( q(x) \) zu einer äquivalenten Einzelkraft \( F_q \) zusammenfassen. Dieses Vorgehen ist immer dann hilfreich, wenn Lagerreaktionen bestimmt werden sollen, aber auch, wenn du den Verlauf von Schnittgrößen abschnittsweise bestimmst.
Deshalb wollen wir uns an dieser Stelle noch einmal genau anschauen, wie du von einer Streckenlast \( q(x) \) \( - \) egal wie einfach oder komplex sie ist \( - \) zur Einzelkraft \( F_q \) kommst.
Ganz allgemein ist eine Einzelkraft ja charakterisiert durch ... na, denk schnell selbst nach, bevor du weiterliest ... ok, ich helfe dir ein bisschen ... es sind drei typische Eigenschaften, die du angeben musst ...
- ...
- ...
- ...
- die Richtung
- den Angriffspunkt und
- den Betrag.
Die Richtung, der Betrag und der Angriffspunkt müssen so gewählt werden, dass sich die "Wirkung nach außen" nicht ändert. Mechanisch gesprochen bedeutet dies, dass die Auswertung der Gleichgewichtsbedingungen (Kräfte- und Momentengleichgewicht) für das System mit der Streckenlast und das System mit der äquivalenten Einzelkraft \( F_q \) auf dasselbe Ergebnis führen muss.
Die Richtung der Einzelkraft \( F_q \) ist identisch der Richtung von \( q(x) \). Warum sollte es anders sein?
Der Betrag von \( F_q \) entspricht der Fläche, die von \( q(x) \) überdeckt ist. Der Angriffspunkt ist der Schwerpunkt der Fläche, die von \( q(x) \) überdekct ist. Die Wirkungslinie von \( F_q \) muss also durch den Schwerpunkt genau dieser Fläche gehen.
Schauen wir uns das an drei Beispielen an.
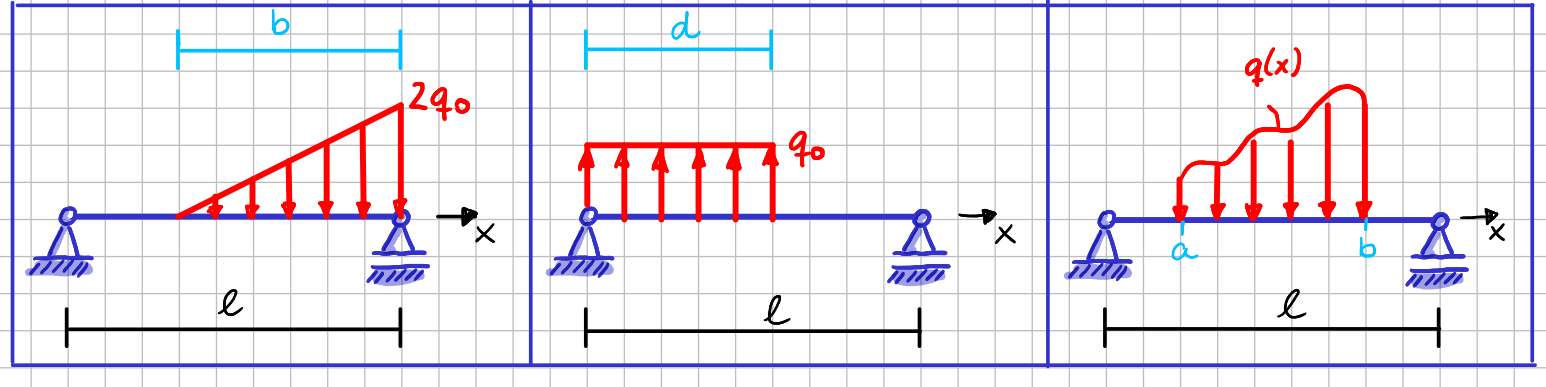
Drei verschiedene Verläufe für Streckenlasten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Drei_verschiedene_Verl%C3%A4ufe_fuer_Streckenlasten.png
Wenn du jetzt also die Anweisungen befolgst, kannst du die Lage der Wirkungslinien und die Richtung von \( F_q \) in allen drei Fällen gleich einzeichnen, oder?
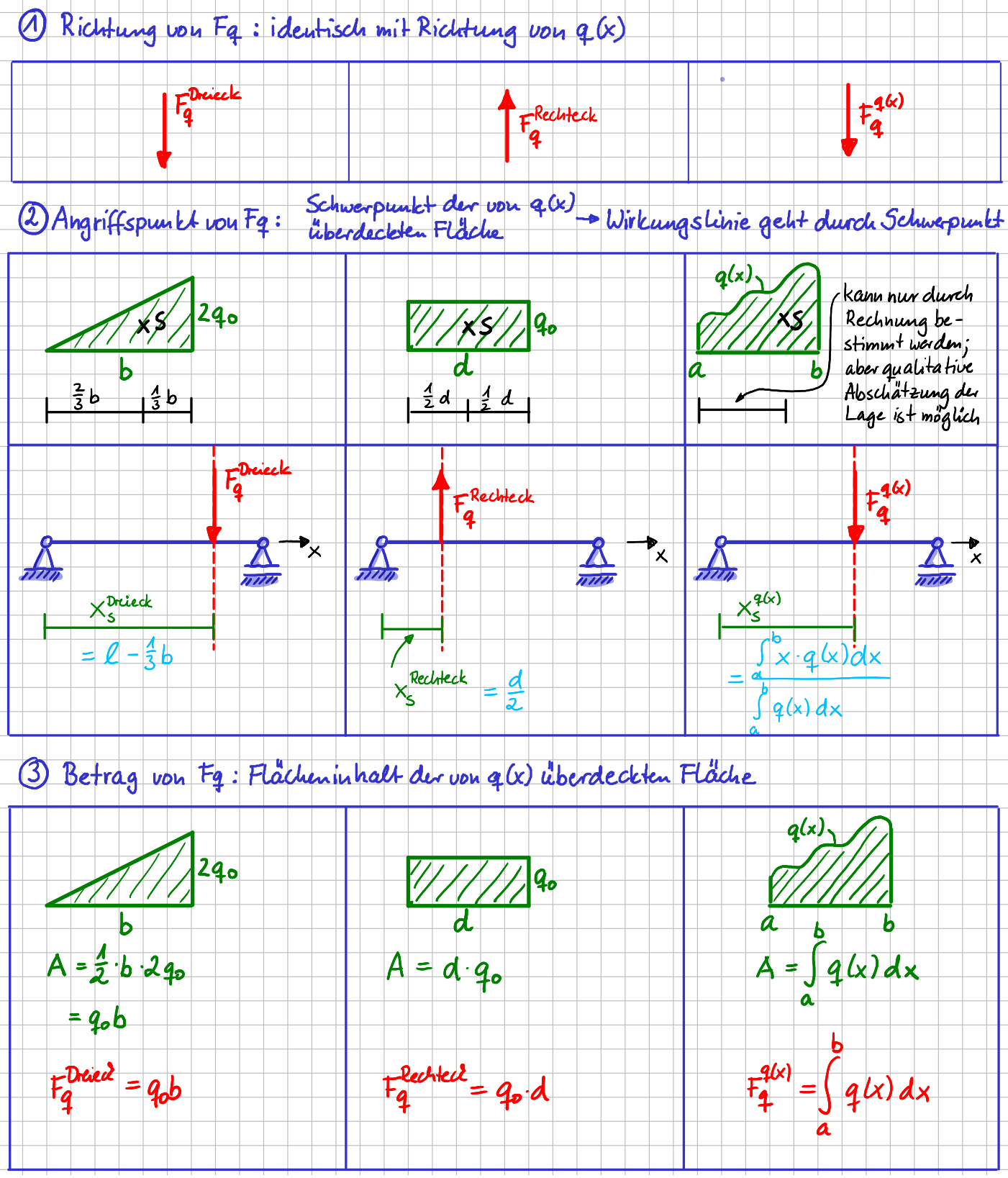
Bestimmung der äquivalenten Einzelkraft \(F_q\)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Bestimmung_der_aequivalenten_Einzelkraft.png
Damit hast du für alle drei Systeme die äquivalente Einzelkraft \(F_q\) bestimmt.
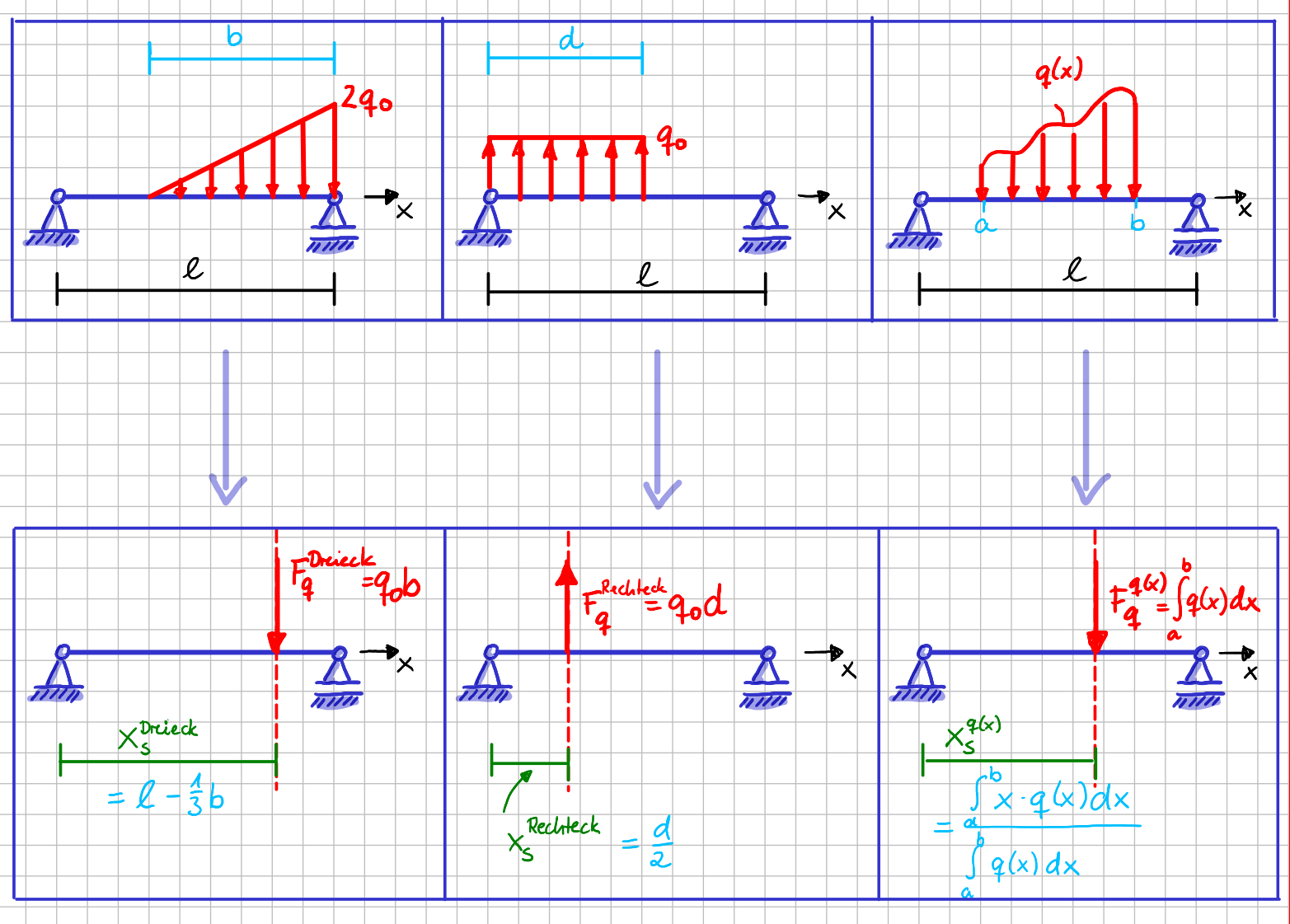
Ausgangssysteme und Ersatzsysteme mit äquivalenter Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Ausgangssysteme_und_Ersatzsysteme_mit_aequivalenter_Einzelkraft.png
Schauen wir nochmal genau auf die Fläche im Fall der rechteckförmigen Streckenlast. Eine Kantenlänge ist \( d \), also eine Länge, die z.B. in \( [\mathrm{m}] \) gegeben sein kann. Die andere Kantenlänge ist \( q_0 \), die z.B. in \( \left[\frac{\mathrm{N}}{\mathrm{m}}\right] \) gegeben sein kann. Das mag dich zunächst irritieren, da Flächen ja die Einheit "Länge \( ^2 \)" also z.B. \( [\mathrm{m}^2] \) haben. Unsere Fläche ist also keine Fläche im klassischen Sinn, was ja wiederum auch total Sinn macht, da wir ja sagen, dass die Streckenlastfläche dem Betrag der Kraft \( F_q \) entspricht. Und der Betrag einer Kraft wird ja bitteschön immer noch in \( [\mathrm{N}] \) angegeben. Wenn wir jetzt also die beiden Kantenlängen unserer Streckenlastfläche mit einander multiplizieren, so gilt für die Einheiten \( [\mathrm{m}] \cdot\left[\frac{\mathrm{N}}{\mathrm{m}}\right] = [\mathrm{N}] \). Die Dimension des Flächeninhalts der Streckenlastfläche ist also \( [\mathrm{N}] \). Und damit hat alles seine Richtigkeit.
Zusammenfassung - Das Wichtigste in Kürze
- die Richtung
\( \rightarrow \) dieselbe wie die der Streckenlast - die Lage der Wirkungslinie
\( \rightarrow \) geht durch den Schwerpunkt der von \( q(x) \) überdeckten Fläche - den Betrag
\( \rightarrow \) entspricht dem Flächeninhalt der von \( q(x) \) überdeckten Fläche
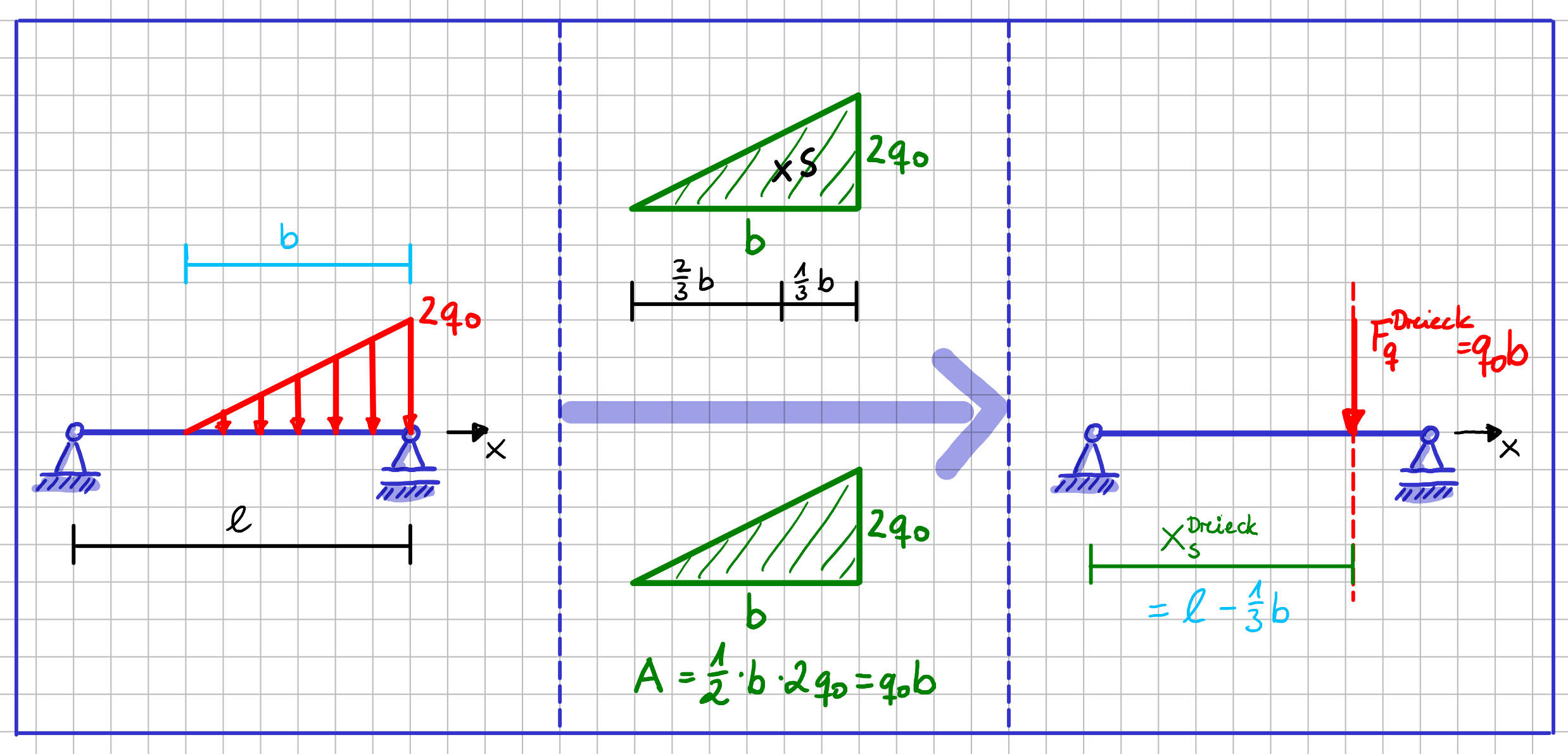
Ausgangssystem und Ersatzsystem mit äquivalenter Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Ausgangssystem_und_Ersatzsystem_mit_aequivalenter_Einzelkraft.png
Arbeitsblatt - Teste dein Wissen
Test - Prüfe dein Wissen
3.3. Seilkraft ohne Reibung
Seilkraft ohne Reibung
Könnte man statt eines Tauziehens auch ein Taudrücken veranstalten? "Komische Frage", denkst du jetzt vielleicht. Mit einem langen Tau zu drücken geht irgendwie nicht. Mit einem ganz kurzen Stück aber schon. Mh.
Und 'n Ooge taudrücken sollten wir vielleicht alle mal viel häufiger.
Aber mal ganz ernsthaft: Die Frage mit dem Tauziehen/-drücken führt uns direkt zur Frage, was ein Seil eigentlich ist. Und du ahnst es schon: Wenn ich diese Frage so stelle, dann meine ich natürlich "Was ist ein Seil als mechanisches Modell?"
Überleg als erstes Mal, wo Seile in der Realität eingesetzt werden. Ein paar Anregungen findest du in den folgenden Bildern.
Was kennzeichnet Seile in all diesen Anwendungen? Es sind Elemente, die
- aus zusammengedrehten oder geflochtenen Fasern oder Drähten bestehen,
- im Verhältnis zum Durchmesser sehr schlank oder lang sind, die
- Zugkräfte übertragen und
- durchhängen, wenn man ein längeres Stück davon hochhebt und sie sind
- je nach Material und Herstellung mehr (z.B. Kletterseil) oder weniger (z.B. Drahtseil) elastisch.
- masselos,
- straff,
- nicht dehnbar,
- ohne Biegesteifigkeit und
- kann ausschließlich Zugkräfte übertragen und
- sein Durchmesser ist gegenüber seiner Länge und allen anderen Abmessungen des Systems vernachlässigbar.
Für einen Kran ist ein ebenes Modell erstellt worden, das du in der nächsten Abbildung siehst. Der Ausleger des Krans ist als Fachwerk modelliert. Die eigentliche Hebevorrichtung für Lasten ist als Rolle mit Radius \( r \) im Modell berücksichtigt worden. Ein Seil führt von der Motoreinheit im Punkt \( D \) wie dargestellt über die Rolle zur Last mit der Gewichtskraft \( G \). Wird die Motoreinheit angesteuert, bewegt sich die Last also je nach Drehrichtung des Motors nach obern oder nach unten.
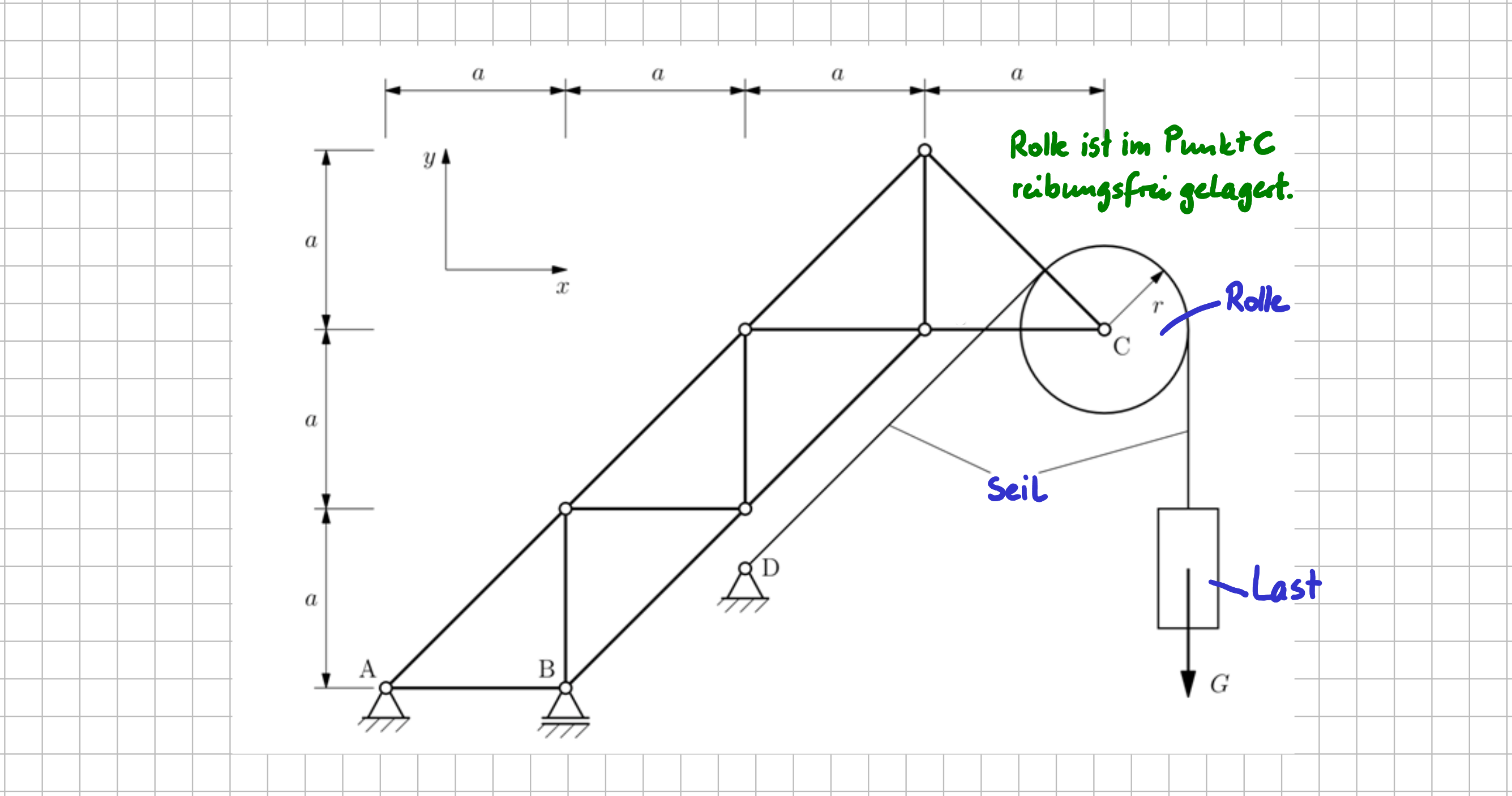
Ebenes Modell eines Krans.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2169/Ebenes_Modell_eines_Krans.png
Aus Sicht des Konstrukteurs des Krans ist es natürlich wünschenswert, dass das Anheben und Senken von Lasten bei einem Kran möglichst reibungsfrei, also möglichst ohne zusätzlichen Energieaufwand, funktioniert. Dementsprechend ist es nur logisch davon auszugehen, dass bei der Auslegung der Lagerung der Rolle konstruktiv darauf geachtet wurde, dass möglichst wenig Reibung vorliegt. Für das Modell ist es daher angemessen anzunehmen, dass an der Lagerstelle gar keine Reibung vorliegt: Die Rolle wird als reibungsfrei gelagert in Punkt \( C \) modelliert. Da die Masse der Rolle im Vergleich zu den zu bewegenden Lasten klein ist, wird die Masse der Rolle vernachlässigt.
Stellt sich die Frage, wie es mit der Kraft im Seil aussieht. Machen wir doch erstmal das, was wir schon gut können: Freischneiden und ein Freikörperbild erstellen. Dabei benenne ich alle Größen, deren Wert noch nicht bekannst sind, mit sinnvollen Namen.
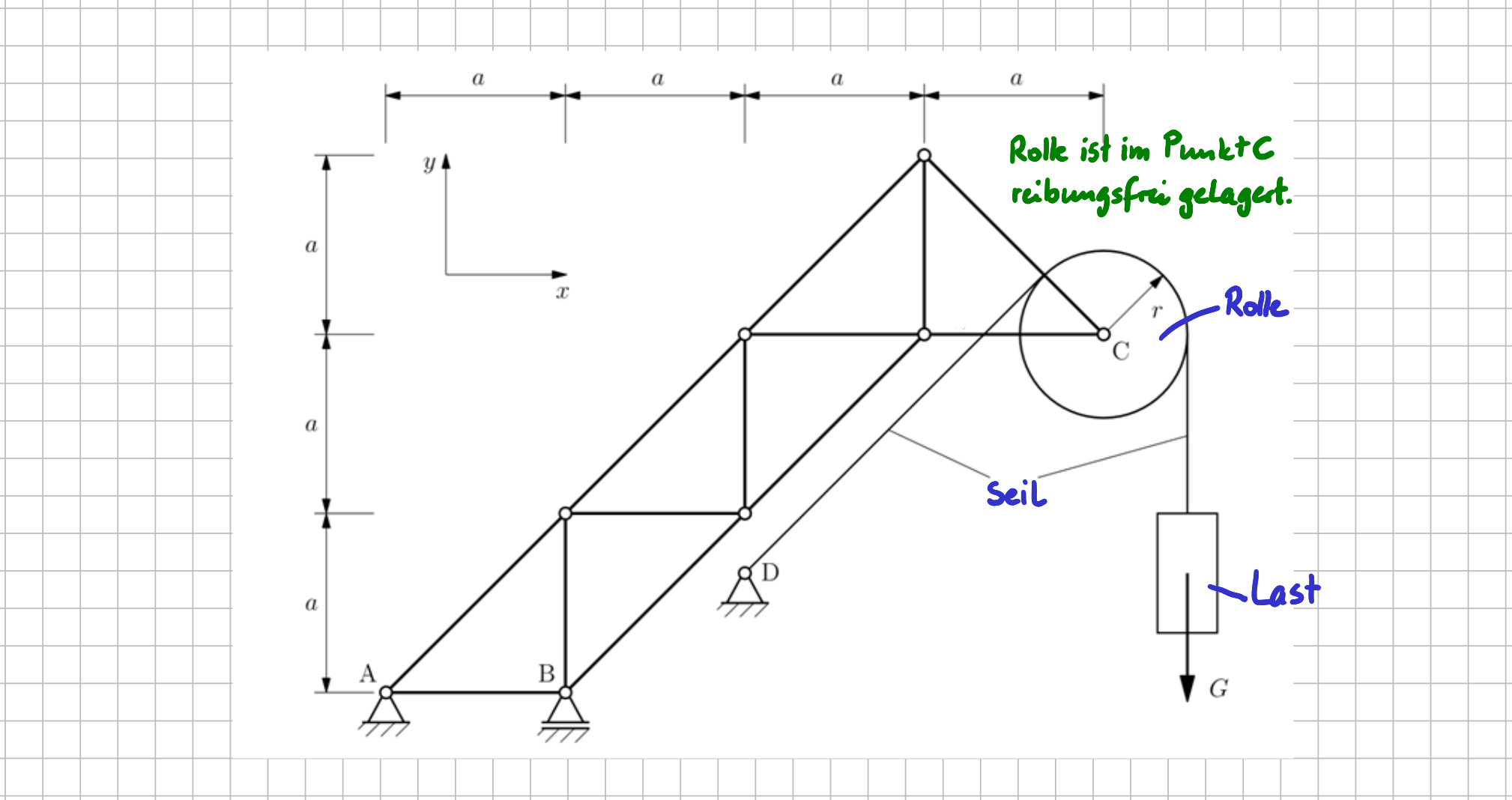
Ebenes Modell eines Krans: Freischneiden der Rolle.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2169/Ebenes_Modell_eines_Krans_Freischneiden_der_Rolle.png
Wenn wir die Rolle freischneiden wollen, müssen wir das Seil an beiden Seiten der Rolle schneiden. Zusätzlich müssen wir noch die Rolle vom eigentlichen Fachwerk, das den Krangrundaufbau modelliert, trennen, also in Punkt \( C \) schneiden .
Mit eingezeichneten Größen an den Schnittstellen, sieht das dann so aus:
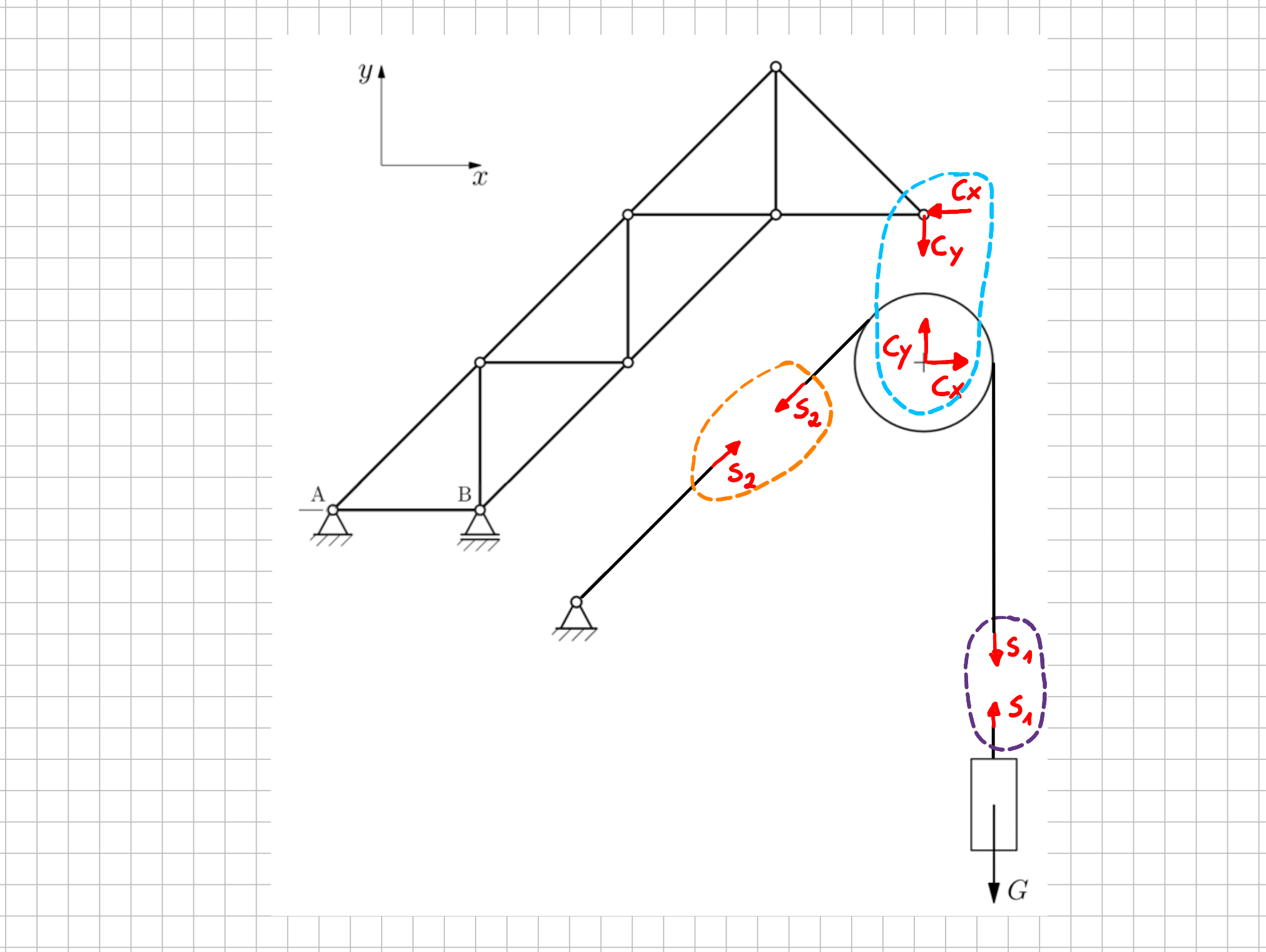
Ebenes Modell eines Krans: Teilfreikörperbild.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2169/Ebenes_Modell_eines_Krans_Teilfreikoerperbild.png
An den Stellen, an denen das Seil geschnitten wurde, habe ich je eine Kraft in Seilrichtung eingezeichnet und natürlich das Prinzip "Actio = Reactio" berücksichtigt. Da Seile nur Zugkräfte übertragen können, ist es einfach nur logisch, die Kräfte "vom Seil weg", also in Zugrichtung einzuzeichnen. Würde ich die Seilkräfte ausrechnen, wüsste ich, dass ich bei dieser Art des Freikörperbilds in jedem Fall etwas Positives herauskommen muss. Passiert das nicht, weiß ich, dass ich mich verrechnet habe und kann auf Fehlersuche gehen. Der Buchstabe \( S \) für Seilkräfte bietet sich einfach an. Und da ich nicht weiß, wie groß die Seilkräfte sind, habe ich sie einfach mit einem fortlaufenden Index nummeriert. Das Lager im Punkt \( C \) ist reibungsfrei und kann eine Kraft in eine beliebige Richtung übertragen, die ich hier wie üblich gleich in Komponenten in die beiden gegebenen Koordinatenrichtungen zerlegt habe.

Ebenes Modell eines Krans: Freikörperbilder von Rolle und Last
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2169/Ebenes_Modell_eines_Krans_Freikoerperbilder_von_Rolle_und_Last.png
Das Gesamtsystem ist im Gleichgewicht und beim Herausschneiden der Rolle und der Last haben wir die auftretenden Reaktionsgrößen berücksichtigt. Deshalb müssen auch Rolle und Last jeweils im Gleichgewicht sein undwirfür können für beide Körper Gleichgewichtsbedingungen aufstellen.
Aus dem Momentengleichgewicht für die Rolle im Punkt /( C /) um die \( z- \)Achse ergibt sich, dass die beiden Seilkräfte \( S_1 \) und \(S_2 \) gleich groß sind. Aus dem Kräftegleichgewicht in \( y- \)Richtung für die Last folgt \(S_1 = G\). Durch die reibungsfrei gelagerte Rolle wird das Seil also lediglich umgelenkt weshalb die Seilkraft "rechts und links" von der Rolle identisch ist und den Wert der Gewichtskraft der Last hat.
Bisher haben wir gesagt, dass die Rolle reibungsfrei gelagert ist. Wenn wir uns das Freikörperbild der Rolle und das Freikörperbild, bei dem zusätzlich noch das Seil von der Rolle getrennt wird, anschauen, wird unmittelbar über den Kontakt zwischen Rolle und Seil noch etwas klar.
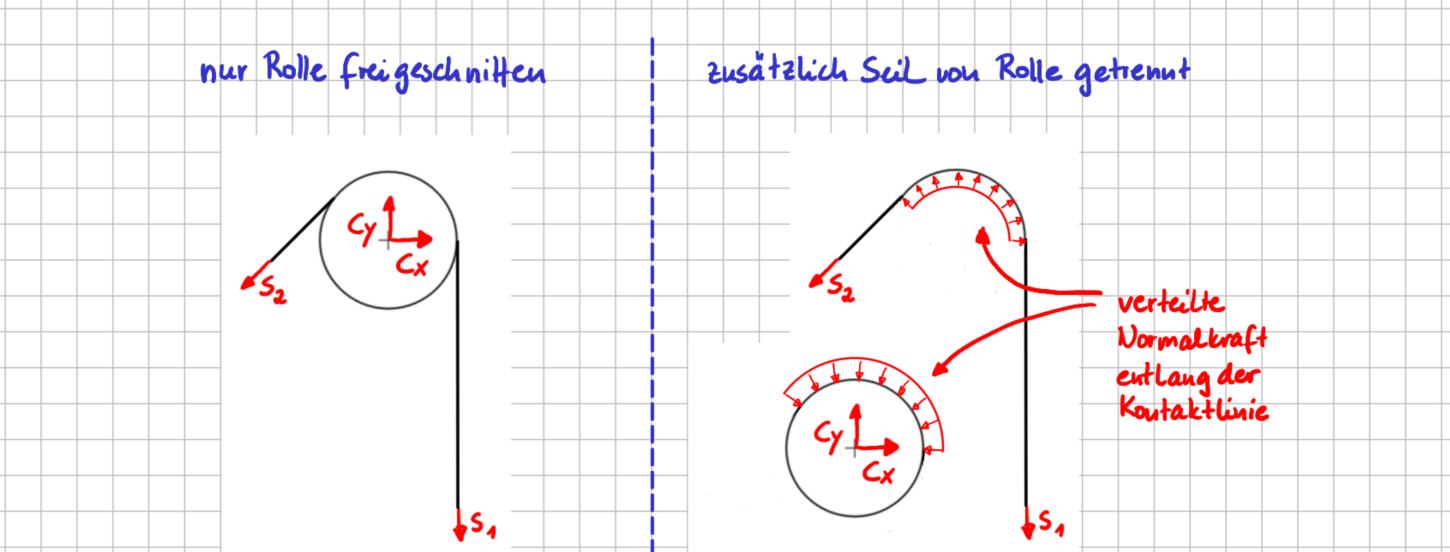
Rolle: Seil noch nicht von Rolle getrennt (links); Seil auch noch von Rolle getrennt (rechts).
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2169/Rolle_Seil_nocht_nicht_getrennt_und_getrennt.png
Zwischen dem Seil und der Rolle wirkt entlang der Kontaktlinie in jedem Fall eine Normalkraft. Sie wurde hier beim Freischneiden als kostant über die Berührlinie verteilt modelliert.
Aber wie sieht es nun mit einer Reibkraftkomponente im Kontakt zwischen Seil und Rolle aus?
Der Kontakt zwischen Seil und Rolle muss reibungsfrei sein. Würde entlang der Kontaktlinie zwischen Seil und Rolle eine Reibkraft wirken, würde die ja ins Momentengleichgewicht eingehen. Das würde ummittelbar zur Folge haben, dass die Seilkräfte \( S_1 \) und \( S_2 \) ungleich wären. Wir haben ja aber gerade eben anhand des Freikörperbildes, in dem das Seil noch nicht von der Rolle getrennt ist, gezeigt, dass die beiden Seilkräfte identisch sind. Wenn eine Rolle reibungsfrei gelagert ist, bedeutet das in der betrachteten Konstellation automatisch, dass auch zwischen Seil und Rolle keine Reibung wirkt. Das unterstreicht nochmal die Aussage, dass das Seil einfach nur umgelenkt wird und die Kraft im Seil sich dadurch nicht ändert.
Wenn die Rolle jetzt einfach als Umlenkung fungieren würde, es also gar kein Lager in der Mitte gäbe und die Rolle fest mit der Umgebung verbunden wäre, was ändert sich dann? Im folgenden Bild ist die "feste Ecke" rechts dargestellt.
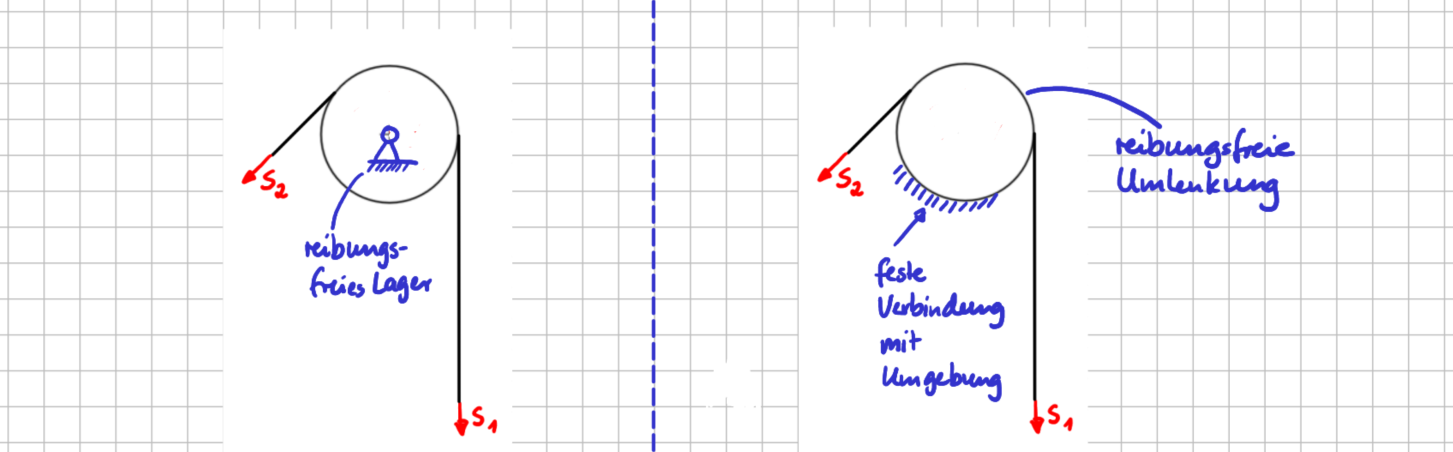
Reibungsfrei gelagerte Rolle (links); Umlenkung mit reibungsfreiem Kontakt zwischen Seil und Kontaktpartner (rechts): die mechanische Funktion ist dieselbe.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2169/Reibungsfreie_Rolle_und_reibungsfreier_Kontakt.png
Rein von der mechanischen Funktion her ändert sich gar nichts, wenn das Seil um eine Geometrie, die die Form eines Kreises hat, umgelenkt wird. Das gilt genau so lange, wie der Kontakt zwischen Seil und Rollengeometrie reibungsfrei ist.
In diesem Video findest du noch einmal viele Punkte aus diesem Abschnitt:
Ganz anders sieht die Welt aus, wenn im Modell Reibung berücksichtigt werden muss. Was sich ändert, wenn der Kontakt zwischen Seil und Kontaktpartner als reibungsbehaftet, also mit Reibung, modelliert werden muss, um die Realität möglichst gut abzubilden, das steht in einem anderen Abschnitt.
3.4. Reibkraft
Reibkraft
In diesem Kapitel beleuchten wir das Thema Reibung aus verschiedenen Perspektiven. Wir starten mit dem, was du aus Alltagserfahrungen kennst und ganz leicht jeder Zeit ausprobieren kannst. Dann nehmen wir das physikalische Verständnis dazu. Und zum Schluss schauen wir, wie man den Einfluss von Reibung mathematisch beschreiben kann.
Alltagserfahrungen
Wetten, dass du ab sofort keinen Stuhl mehr verschieben kannst, ohne an Reibung zu denken? Und auch Science-Fiction-Filme wirst du vermutlich nach dem Durcharbeiten dieses Kapitels nicht mehr schauen können, ohne an Reibung zu denken. Ich wollte dich nur vorab warnen. Aber jetzt starten wir erstmal ganz irdisch.
Denk doch als erstes mal selber darüber nach, wo dir im Alltag überall Reibung begegnet.

Ohne Reibung wäre vieles gar nicht möglich ... oder würde nicht passieren.
Weitere Informationen
Marco Verch, master1305, drobotdean, gpointstudio, senivpetro, teksomolika, fxquadro
freepik
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Ohne_Reibung_waere_vieles_gar_nicht_moeglich.png
Vielleicht hast du kürzlich den Stuhl nach dem Essen wieder unter den Tisch geschoben. Das ging nicht „einfach so“, sondern da war ein „gewisser Widerstand“ zu spüren, oder? Genauer gesagt, war da ein doppelter „Widerstand“ zu spüren: Erst, musstest du eine gewisse Kraft aufbringen, bis sich das Sitzmöbel überhaupt in Bewegung gesetzt hat. Und als es sich bewegt hat, war da auch ein „Widerstand zu spüren“. Schon in dieser einfachen Situation kannst du ganz viele Aspekte von „Reibung“ spüren und beobachten. Nehmen wir mal an, du schiebst den Stuhl nach vorne. Dann wirkt die Reibkraft auf den Stuhl nach hinten. Die so genannte Gleitreibungskraft wirkt also entgegen der Bewegungsrichtung. Und das ist immer so. Und dass du erst eine gewisse Mindestkraft aufbringen musst, bevor sich der Stuhl überhaupt in Bewegung setzt, das hat auch mit Reibung zu tun. Es gibt nämlich auch noch die sogenannte Haftreibung, genauer gesagt einen Maximalwert der Haftreibungskraft, der erstmal überwunden werden muss, bevor der Stuhl verschoben werden kann.
Manche Stühle sind mit Filzgleitern unter den Beinen versehen. Andere haben Kunststoffgleiter. Warum ist das so? Also, warum gibt es überhaupt solche Gleiter und dann aus verschiedenen Materialien? Die Filzgleiter werden verwendet, wenn ein Stuhl auf Holz zum Einsatz kommt. Die Gleiter aus Kunststoff werden normalerweise verwendet, wenn ein Stuhl auf Teppich steht. Die Materialien für die Gleiter werden also so ausgewählt, dass die Reibung zwischen Stuhl und Boden möglichst gering ist. Die Materialpaarung an einer Kontaktstelle hat also einen Einfluss auf die Größe der Reibkraft. Aber selbst, wenn die Materialpaarung bleibt: es gibt weitere Einflüsse auf die Größe der Reibkraft. Vielleicht hast du Folgendes schon mal erlebt: Während du mit gewissen Schuhen bei trockenen Verhältnissen noch guten Halt hast, rutscht du sobald es nass ist, immer wieder weg. Und Reifen, die im Sommer eine gute Kraftübertragung vom Fahrzeug auf den Asphalt ermöglichen, drehen im Winter bei geringeren Temperaturen plötzlich immer wieder durch. Warum fahren Formel-1-Fahrer manchmal mit Slicks und manchmal nutzen sie mehr oder weniger stark profilierte Reifen? Es kommt also nicht nur auf die Materialpaarung an sich, sondern auch auf die Umgebungsbedingungen (z.B. Temperatur, Feuchte) und auch die Oberflächen der Kontaktpartner an.
Und dann spielt es ja bei einer festen Materialpaarung und festen Umgebungsbedingungen auch noch eine Rolle, wie die Oberflächen der beiden Kontaktpartner beschaffen sind.
Wenn du jetzt denkst: Puuh, und das alles soll in der Mechanik in den Gleichungen berücksichtigt werden? Naja, zumindest die wesentlichen Phänomene, die du im Alltag beobachten kannst. Das Thema „Reibung“ ist in der Tat ein ganz eigenes Forschungsthema, mit dem man sich viele Jahre beschäftigen kann. Aber wie so oft gilt ja: mit ganz einfachen Ansätzen kommt man schon ein großes Stück weit. Und genau diese Ansätze wollen wir uns genauer ansehen.
Physikalisches Verständnis
Holen wir doch einfach mal die Physik detaillierter ins Boot. Eine Reibkraft tritt immer dann zwischen zwei Objekten auf, wenn zwischen ihnen auch eine Kraft senkrecht zum Berührpunkt oder der Berührfläche, also eine sogenannte Normalkraft wirkt. Wenn du also eine Kiste über den Boden schiebst, dann braucht es eine Kraft senkrecht zum Boden, die sogenannte Normalkraft, die die Gewichtskraft kompensiert. Da hier also die Voraussetzung, dass es eine Normalkraft gegeben muss, erfüllt ist, wirkt auch eine Reibkraft zwischen Kiste und Boden, wenn du versuchst, sie in Bewegung zu setzen oder die Kiste verschiebst.Wenn du die Kiste genau an einer Wand entlang schiebst, wirkt zwischen Wand und Kiste keine Reibkraft, solange du mit deiner Hand die Kraft exakt parallel zur Wand auf die Kiste aufbringst. Es gibt ja schlicht und einfach keine Kraft, die senkrecht zur Wand wirkt. Und wo keine Normalkraft, da auch keine Reibkraft.

Normalkraft als Voraussetzung für das Auftreten von Reibung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Normalkraft_als_Voraussetzung_fuer_das%20Auftreten_von_Reibung.png
Tja, und wie ist das jetzt mit der Fortbewegung im Raumschiff im Weltall? Wieso kann sich die Besatzung der Enterprise gehend fortbewegen? Und wieso geht das auf der ISS nicht? Mehr dazu im Arbeitsblatt.
Kommen wir nochmal zu dem Punkt zurück, dass du auf einen Gegenstand eine Kraft ausüben kannst, ohne dass er sich bewegt. Je nachdem, wie feinmotorisch du unterwegs bist: Schnapp dir einfach mal einen leichten bis mittelschweren Gegenstand auf einem Tisch und probiere aus, wie doll du mit deinem Zeigefinger dagegendrücken kannst, bevor er anfängt sich zu bewegen. Und jetzt bleibst du mit der Kraft, die du aufbringst gerade unter dieser Grenze.
Merk dir, wie sich die Kraft anfühlt, die du gerade aufbringst. Wenn du jetzt den Gegenstand in Bewegung bringen willst, musst du ein bisschen mehr Kraft aufbringen. Und danach ist die Kraft sogar ein bisschen geringer, wenn du den Gegenstand mit konstanter Geschwindigkeit über den Tisch schiebst, oder?
Der Grund dafür, dass du eine Mindestkraft aufbringen musst, bevor sich der Gegenstand in Bewegung setzt, liegt darin, dass die beiden berührenden Oberflächen nicht glatt sind.
Selbst ein Glasbecher und ein geschliffener Holztisch, deren Oberfläche mit dem bloßen Auge sehr glatt wirken, sind es auf mikroskopischer Ebene nicht. Die Oberflächen sind rauh und die Spitzen, die sich auf beiden Oberflächen befinden, sind ineinandergeschoben und verhaken sich ein wenig.

Anschieben eines Glases auf einem Tisch
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Anschieben_eines_Glases_auf_einem_Tisch.png
Erst, wenn die Kraft, die du aufbringst, so groß ist, dass sich diese Spitzen voneinander lösen, setzt sich der Glasbecher im Bild in Bewegung. Und wenn die Spitzen erstmal voneinander getrennt sind und Bewegung vorliegt, schieben sie sich auch nicht wieder vollständig ineinander. Deswegen nimmt ist die Kraft, die du brauchst, um den Gegenstand mit konstanter Geschwindigkeit über den Tisch zu schieben, auch ein wenig geringer, als die Losbrechkraft.
Wenn der Tisch jetzt wieder noch feucht wäre, wäre es für die Spitzen einfacher, sich voneinander zu trennen. Die Losbrechtkraft wäre also geringer, als bei einer trockenen Oberfläche.
Und wie beschreibt man das jetzt alles?
Wenn du jetzt denkst: "Puuh, das sind ja ganz schön viele Phänomene, die es bei Reibung gibt. Das alles soll ich mathematisch beschreiben können?" Ja, ganz genau das. Und du wirst sehen, es ist eigentlich ganz einfach und vor allem logisch. Wie immer fangen wir mit dem an, was du schon kennst.
Stell dir also als erstes noch einmal vor, dass du auf einen Gegenstand eine beliebige Kraft aufbringst, deren Größe so ist, dass sich der Gegenstand nicht bewegt. Der Gegenstand befindet sich dann im Gleichgewicht. Das bedeutet, dass du alles anwenden kannst, was du bisher gelernt hast, da ja noch gar nichts neu ist: Freischneiden und Gleichgewichtsbedingungen aufstellen. Das machen wir doch einfach mal für ein Objekt mit der Masse \( m \). Zeichne als erstes das Freikörperbild für den Fall, dass nur die Gewichtskraft wirkt, du also noch gar nicht mit deinem Finger dagegendrückst. Im zweiten Fall kommt dann zusätzlich noch die Kraft \( F_{\mathrm{Finger}} \), die durch deinen Finger auf den Gegenstand ausgeübt wird, dazu.
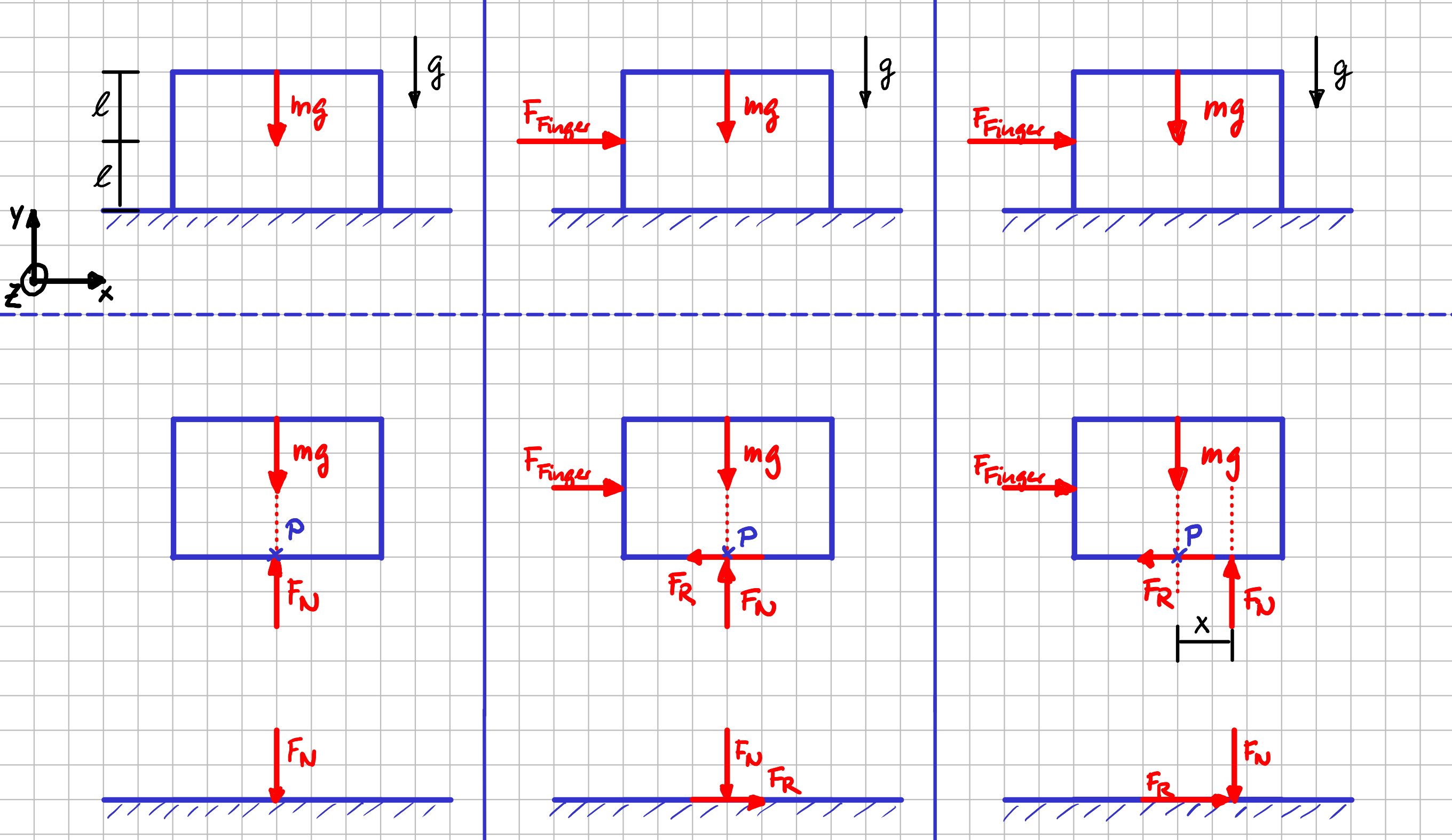
System und zwei Varianten für das Freikörperbild
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/System_und_zwei_Varianten_fuer_das_Freikoerperbild.png
Und? Wie sehen deine beiden Freikörperbilder aus? Ich habe die Normalkraft mit \( F_N \) und die Reibkraft mit \( F_R \) bezeichnet. Beim linken Freikörperbild \( - \) ohne Belastung durch die Fingerkraft \( - \) sind wir uns bestimmt einig. Aber welches Freikörperbild ist korrekt, wenn auch die Kraft durch deinen Finger auf den Gegenstand wirkt? Ist es das mittlere Freikörperbild? Oder das rechte? Oder noch eine andere Variante? Wenn du nicht gleich eine klare Antwort hast, stell doch einfach mal für alle drei Varianten die Gleichgewichtsbedingungen auf.
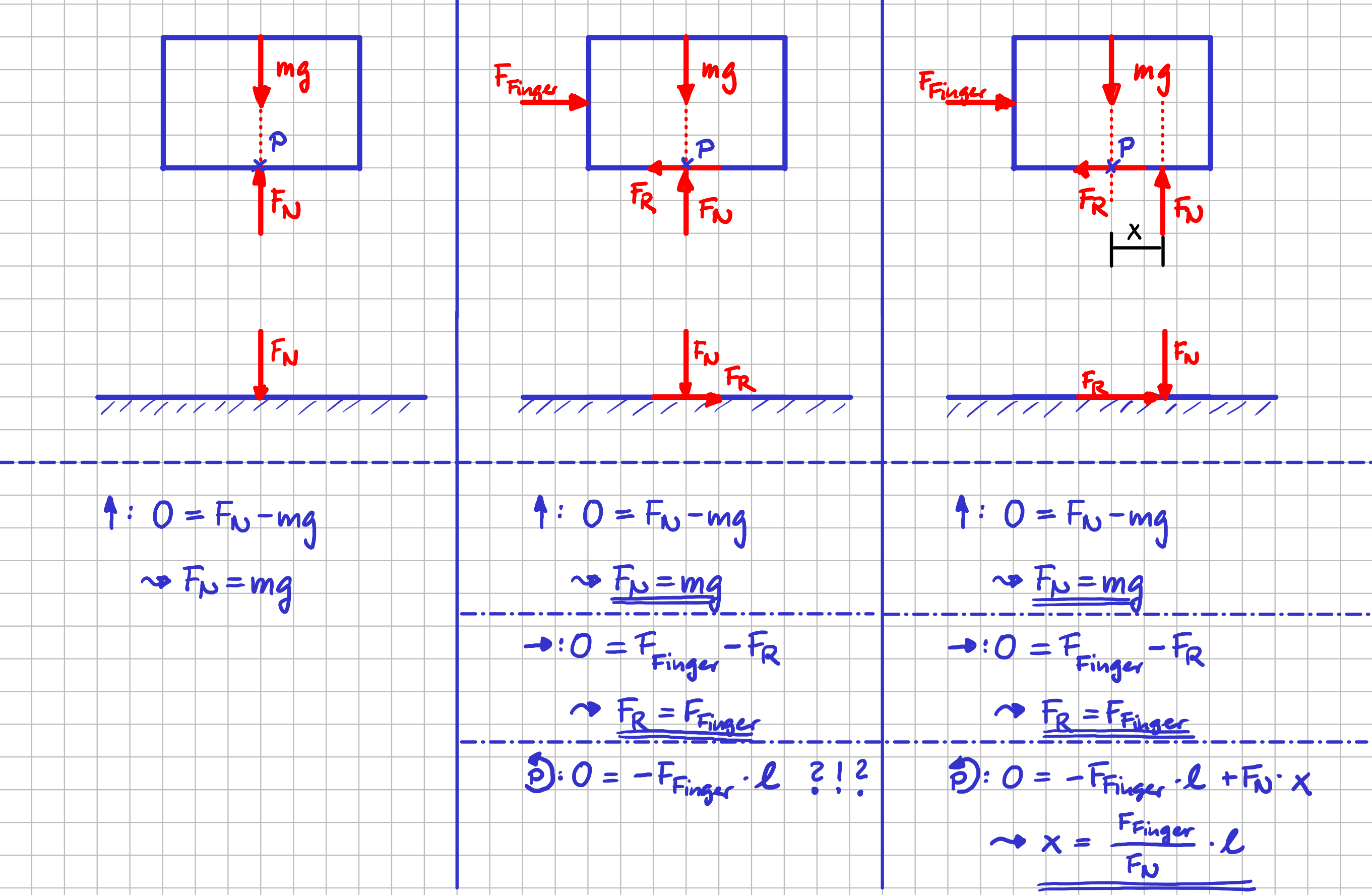
Gleichgewichtsbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Gleichgewichtsbedingungen.png
In dem Fall, in dem nur die Gewichtskraft angreift, ist alles klar, oder? Zwischen Kiste und Boden wirkt als Reaktionskraft nur die Normalkraft \( F_N \) und ihr Betrag ist genauso groß wie die Gewichtskraft.
Schauen wir uns die Gleichgewichtsbedingungen für die beiden Varianten, in denen die Fingerkraft auch mit angreift, mal im Detail an.
\( y \)-Richtung
Auch hier gilt in beiden Fällen, dass die Normalkraft \( F_N \) der Gewichtskraft \( mg \) entgegenwirkt und der Betrag der Normalkraft genauso groß ist, wie die Gewichtskraft.
\( x \)-Richtung
Aus dem Kräftegleichgewicht in \( x \)-Richtung folgt, dass Fingerkraft \( F_{\mathrm{Finger}} \) und Reibkraft \( F_R \) entgegengesetzt gerichtet ist. Außerdem sind sie beide vom Betrag her gleich groß. Hier gibt es also auch keinen Unterschied.
\( z \)-Richtung
Beim Momentengleichgewicht um die \( z \)-Achse im Bezugspunkt \( P \) bekommst du unterschiedliche Ergebnisse. Im mittleren Fall müsste entweder die durch den Finger aufgebrachte Kraft oder die Länge \( \ell \) Null sein. Mmh, das klingt irgendwie komisch bzw. schlicht und einfach falsch. Weder die Kraft och die Länge sind Null.
Bei der rechten Variante, in der die Normalkraft nicht im Punkt \( P \), sondern rechts davon angreift, kannst du über das Momentengleichgewicht bestimmen, wie groß der Abstand \( x \) der Wirkungslinie der Normalkraft vom Punkt \( P \) sein muss, damit das Momentengleichgewicht erfüllt ist. Das sieht alles sehr vernünftig aus!
Fazit:
- Das mittlere Freikörperbild ist falsch.
- Nur durch Anwenden dessen, was du bereits kennst (Freischneiden und Gleichgewichtsbedingungen aufstellen), hast du hergeleitet, dass der Angriffspunkt der Normalkraft davon abhängt, wie groß die vom Finger aufgebrachte Kraft ist: Je größer die Kraft ist, desto größer ist \( x \).
Und wenn du jetzt noch einen kleinen Schritt weiterdenkst: Du kannst ja nach und nach die Fingerkraft, die du aufbringst, immer weiter erhöhen. Wenn wir annehmen, dass die Kiste dabei die ganze Zeit haftet, also nicht anfängt zu rutschen, dann würde \( x \) immer größer werden, was bedeutet, dass der der Angriffspunkt der Normalkraft immer weiter nach rechts wandert. Und wenn jetzt der Angriffspunkt der Normalkraft in der Ecke, also bei \( x=\frac{3}{2}\ell \) angekommen ist? Was passiert dann?
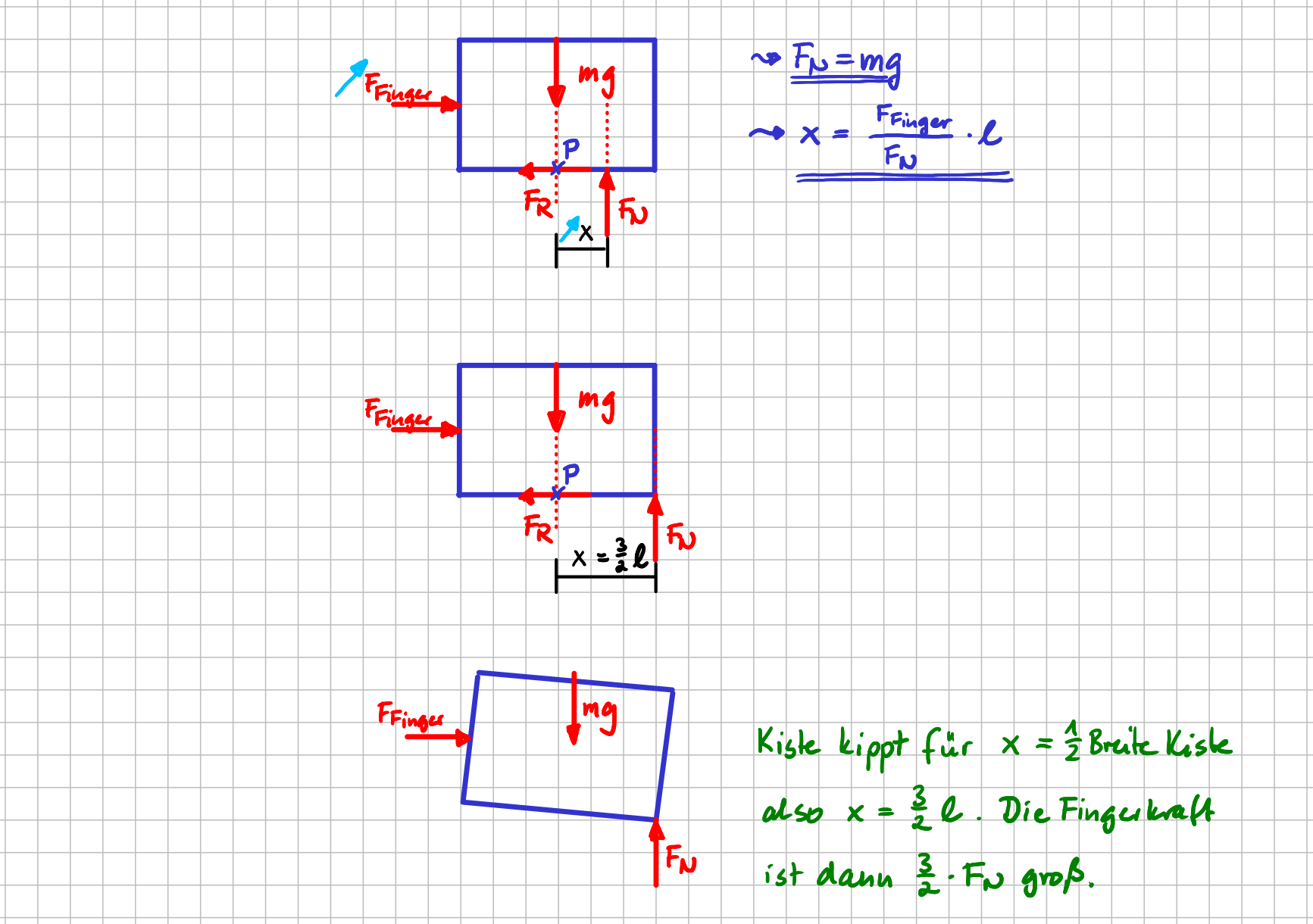
Bedingung dafür, dass die Kiste kippt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Bedingungen_dafuer_dass_eine_Kiste_kippt.png
Dann beginnt die Kiste zu kippen. Probier das mal mit einem Umzugskarton oder auch mit einem Küchenstuhl aus. Kleiner Tipp: Wenn dein Versuchsobjekt erst anfängt zu rutschen, bevor es kippt, dann kannst du die eine Ecke auch einfach festhalten oder irgendwas darunterlegen, so dass der Kontakt zwischen Objekt und Boden möglichst rauh ist.
- Die Richtung der Normalkraft ist immer senkrecht zur Oberfläche. Die Richtung der Reibkraft ist wiederum senkrecht zur Richtung der Normalkraft.
- So lange keine relative Bewegung zwischen zwei Körpern vorliegt, ist die Reibkraft wie eine Reaktionskraft in einem Lager. Ihre Richtung und ihr Betrag lässt sich „wie immer“ aus den Gleichgewichtsbedingungen berechnen. Man sagt „Es liegt Haftreibung vor.“. Und im Fall der Haftreibung ist die Reibkraft vom Typ „Reaktionskraft“.
- Bei der Normalkraft ist von vorneherein immer physikalisch klar, in welche Richtung sie wirkt: AUF die jeweiligen Körper zu. Es macht also Sinn, sie von vornherein auch in diese Richtung im Freikörperbild einzuzeichnen.
- Die Lage der Wirkungslinie der Normalkraft bei einem flächigen Kontakt, so wie wir ihn in unserem Beispiel mit der Kiste haben, ist so, dass das System im Gleichgewicht ist. In unserem Beispiel bedeutet das, dass die Wirkungslinie rechts von der Mittellinie der Kiste liegt. Die genaue Position lässt sich aus dem Momentengleichgewicht bestimmen.
- Kippen tritt immer dann auf, wenn die Normalkraft aufgrund der Art und Weise, wie die anderen äußeren Belastungen wirken, in eine der Ecken des Objektes 'wandert'
- die Richtung,
- den Betrag und
- die Lage der Wirkungslinie.
| Paarung | Gleitreibungskoeffizient \( \mu \) |
|---|---|
| Stahl - Stahl | 0,1 |
| Stahl - Beton | 0,2 |
| Stahl - Eis | 0,01 |
- Richtung entgegen der Bewegungsrichtung
- \( |\vec{F}_R| \propto |\vec{F}_N| \rightarrow |\vec{F}_R| = \mu \cdot |\vec{F}_N| \)
- Lage: in der Berührfläche
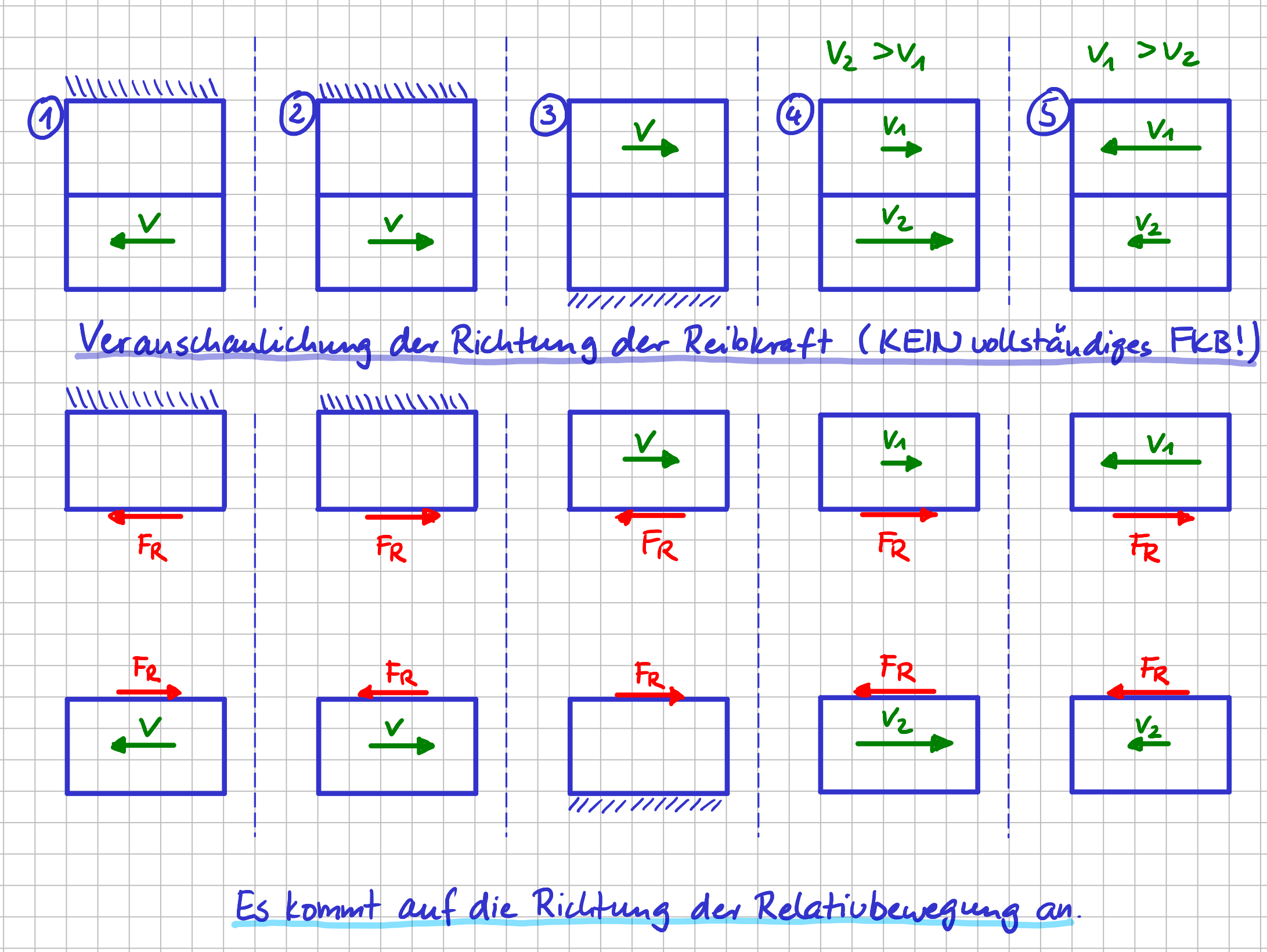
Richtung der Reibkraft für verschiedene Fälle
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Richtung_der_Reibkraft_fuer_verschiedene_Faelle.png
| Paarung | Gleitreibungskoeffizient \(\boldsymbol\mu \) |
Haftreibungskoeffizient \( \boldsymbol\mu_0 \) |
|---|---|---|
| Stahl - Stahl |
0,1 |
0,2 |
| Stahl - Beton |
0,2 |
0,35 |
| Stahl - Eis |
0,01 |
0,03 |
Wie geht man jetzt konkret bei Aufgaben vor?
- Liegt Haftreibung vor, behandelst du die Reibkraft wie jede andere Reaktionskraft auch. Durch Auswerten der Gleichgewichtsbedingungen bekommst du Betrag und Richtung heraus.
- Liegt Gleitreibung vor, zeichnest du die Richtung der Reibkraft entgegen der Bewegungsrichtung am Körper ein und berechnest den Betrag über \( F_R=\mu \cdot F_N \).
Zusammenfassung - Das Wichtigste in Kürze
Die Reibkraft ist eine Kraft, die je nach Bedingungen im System in zwei unterschiedlichen 'Arten' auftritt: als Haftreibung und als Gleitreibung.
\( \boldsymbol\mu \) ist der Gleitreibungskoeffizient und \( \boldsymbol\mu_0 \) ist der Haftreibungskoeffizient.
Haftreibung und Gleitreibung und was sie charakterisiert
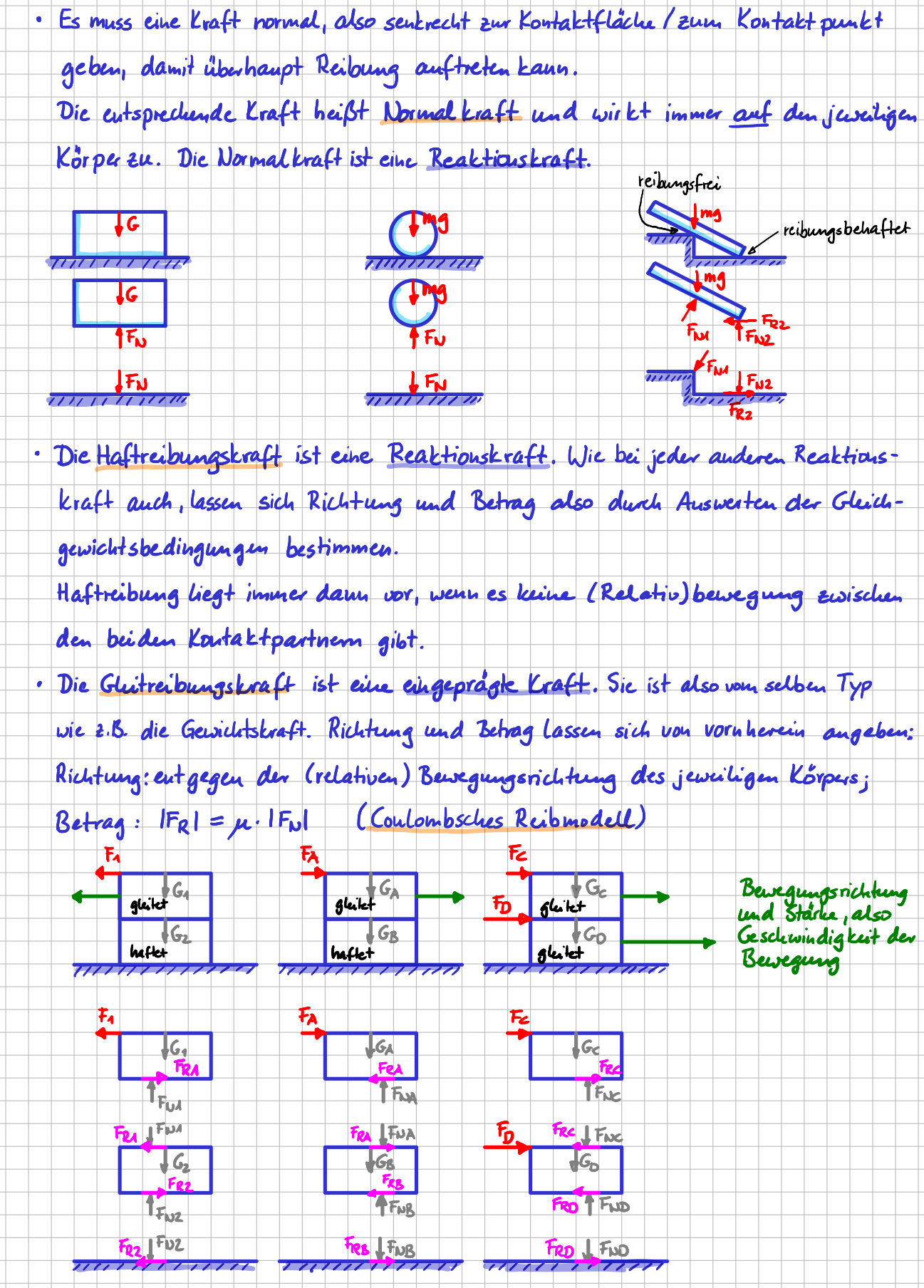
Haftreibung und Gleitreibung und was sie charakterisiert
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Haftreibungs_und_Gleitreibungskraft_und_was_sie_charakterisiert.png
Beispiel, bei dem alle Reibungszenarien auftreten können
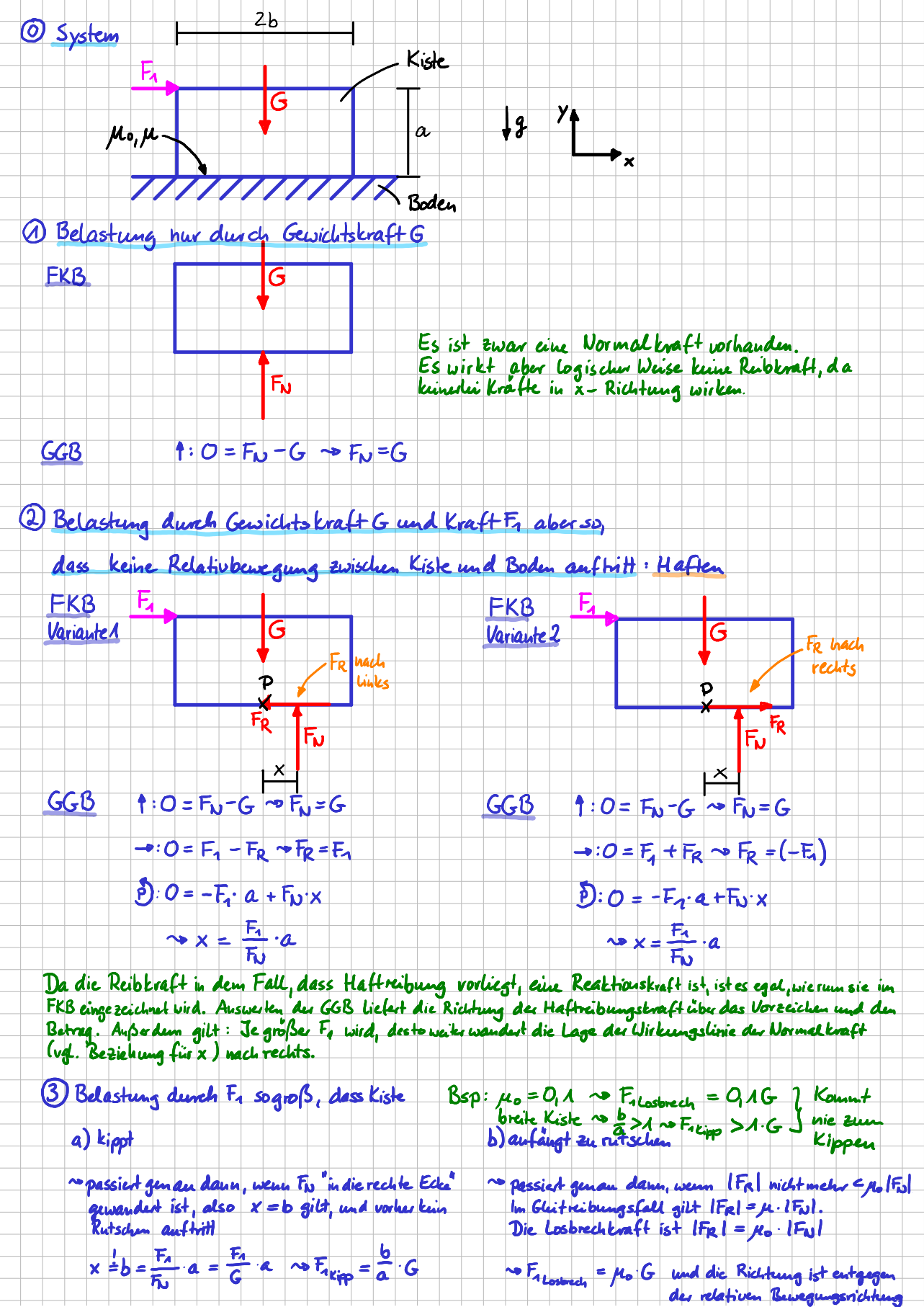
Beispiel, in dem alle Reibungsszenarien auftreten können
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Beispiel_alle_Reibungsszenarien.png
Vorgehen bei Reibungsaufgaben
Wenn nicht von vornherein bekannt ist, ob Haft- oder Gleitreibung vorliegt, rechnest du als erstes so, als ob Haftreibung vorliegen würde. Wenn du denBetrag für \( F_R \) durch Auswerten der Gleichgewichtsbedingungen bestimmt hast, prüfst du, ob deine Annahme, das Haftreibung vorliegt, korrekt war. Gilt \( |F_R| < \mu_0 \cdot |F_N| \) liegt in der Tat Haftreibung vor. Wenn diese Bedingung nicht erfüllt ist, liegt Gleitreibung vor. Der durch Auswerten der Gleichgewichtsbedingungen erhaltene Wert für \( F_R \) ist nicht korrekt, denn es gilt \( |F_R| = \mu \cdot |F_N| \) und die Richtung der Gleitreibungskraft ist entgegen der relativen Bewegungsrichtung.
Arbeitsblatt - Teste dein Wissen
Wilmas Mechanikwelt
Verflixte Reibung Ich liebe Eis. Joghurt-Feige und Joghurt-Heidelbeere mag ich besonders gerne. Natürlich schmeckt Eis besser, wenn es nicht gerade regnet. Aber Eis geht ja eigentlich immer. Was total doof ist: Meine 5-Meter-Schleppleine wickelt sich immer um die Tischbeine und Stuhlbeine. Das freie Leinenende liegt einfach auf dem Boden. Kannst du erklären, warum ich irgendwann so doll ziehen kann, wie ich will? Ich komme einfach nicht mehr von der Stelle. Was hat das mit Reibung zu tun? Kleiner Tipp: Es hat nicht nur mit Seilreibung zu tun. "Normale" Reibung spielt auch noch eine Rolle. Wenn du eine Lösung zu dem Rätsel hast, schreib gerne an diese Emailadresse. Dann schreibe ich deine Lösung hier mit rein. Bin schon sehr gespannt auf deine Ideen.
Verfixte Reibung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Verflixte_Reibung.png

