Kraft: Reibkraft

3. Verschiedene Kraftarten ganz nah

3.4. Reibkraft

Reibkraft

In diesem Kapitel beleuchten wir das Thema Reibung aus verschiedenen Perspektiven. Wir starten mit dem, was du aus Alltagserfahrungen kennst und ganz leicht jeder Zeit ausprobieren kannst. Dann nehmen wir das physikalische Verständnis dazu. Und zum Schluss schauen wir, wie man den Einfluss von Reibung mathematisch beschreiben kann.

Alltagserfahrungen

Wetten, dass du ab sofort keinen Stuhl mehr verschieben kannst, ohne an Reibung zu denken? Und auch Science-Fiction-Filme wirst du vermutlich nach dem Durcharbeiten dieses Kapitels nicht mehr schauen können, ohne an Reibung zu denken. Ich wollte dich nur vorab warnen. Aber jetzt starten wir erstmal ganz irdisch.

Denk doch als erstes mal selber darüber nach, wo dir im Alltag überall Reibung begegnet.

Ohne Reibung wäre vieles gar nicht möglich ... oder würde nicht passieren.

Weitere Informationen

Marco Verch, master1305, drobotdean, gpointstudio, senivpetro, teksomolika, fxquadro
freepik
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Ohne_Reibung_waere_vieles_gar_nicht_moeglich.png

Vielleicht hast du kürzlich den Stuhl nach dem Essen wieder unter den Tisch geschoben. Das ging nicht „einfach so“, sondern da war ein „gewisser Widerstand“ zu spüren, oder? Genauer gesagt, war da ein doppelter „Widerstand“ zu spüren: Erst, musstest du eine gewisse Kraft aufbringen, bis sich das Sitzmöbel überhaupt in Bewegung gesetzt hat. Und als es sich bewegt hat, war da auch ein „Widerstand zu spüren“. Schon in dieser einfachen Situation kannst du ganz viele Aspekte von „Reibung“ spüren und beobachten. Nehmen wir mal an, du schiebst den Stuhl nach vorne. Dann wirkt die Reibkraft auf den Stuhl nach hinten. Die so genannte Gleitreibungskraft wirkt also entgegen der Bewegungsrichtung. Und das ist immer so. Und dass du erst eine gewisse Mindestkraft aufbringen musst, bevor sich der Stuhl überhaupt in Bewegung setzt, das hat auch mit Reibung zu tun. Es gibt nämlich auch noch die sogenannte Haftreibung, genauer gesagt einen Maximalwert der Haftreibungskraft, der erstmal überwunden werden muss, bevor der Stuhl verschoben werden kann.
Manche Stühle sind mit Filzgleitern unter den Beinen versehen. Andere haben Kunststoffgleiter. Warum ist das so? Also, warum gibt es überhaupt solche Gleiter und dann aus verschiedenen Materialien? Die Filzgleiter werden verwendet, wenn ein Stuhl auf Holz zum Einsatz kommt. Die Gleiter aus Kunststoff werden normalerweise verwendet, wenn ein Stuhl auf Teppich steht. Die Materialien für die Gleiter werden also so ausgewählt, dass die Reibung zwischen Stuhl und Boden möglichst gering ist. Die Materialpaarung an einer Kontaktstelle hat also einen Einfluss auf die Größe der Reibkraft. Aber selbst, wenn die Materialpaarung bleibt: es gibt weitere Einflüsse auf die Größe der Reibkraft. Vielleicht hast du Folgendes schon mal erlebt: Während du mit gewissen Schuhen bei trockenen Verhältnissen noch guten Halt hast, rutscht du sobald es nass ist, immer wieder weg. Und Reifen, die im Sommer eine gute Kraftübertragung vom Fahrzeug auf den Asphalt ermöglichen, drehen im Winter bei geringeren Temperaturen plötzlich immer wieder durch. Warum fahren Formel-1-Fahrer manchmal mit Slicks und manchmal nutzen sie mehr oder weniger stark profilierte Reifen? Es kommt also nicht nur auf die Materialpaarung an sich, sondern auch auf die Umgebungsbedingungen (z.B. Temperatur, Feuchte) und auch die Oberflächen der Kontaktpartner an.
Und dann spielt es ja bei einer festen Materialpaarung und festen Umgebungsbedingungen auch noch eine Rolle, wie die Oberflächen der beiden Kontaktpartner beschaffen sind.
Wenn du jetzt denkst: Puuh, und das alles soll in der Mechanik in den Gleichungen berücksichtigt werden? Naja, zumindest die wesentlichen Phänomene, die du im Alltag beobachten kannst. Das Thema „Reibung“ ist in der Tat ein ganz eigenes Forschungsthema, mit dem man sich viele Jahre beschäftigen kann. Aber wie so oft gilt ja: mit ganz einfachen Ansätzen kommt man schon ein großes Stück weit. Und genau diese Ansätze wollen wir uns genauer ansehen.

Physikalisches Verständnis

Holen wir doch einfach mal die Physik detaillierter ins Boot. Eine Reibkraft tritt immer dann zwischen zwei Objekten auf, wenn zwischen ihnen auch eine Kraft senkrecht zum Berührpunkt oder der Berührfläche, also eine sogenannte Normalkraft wirkt. Wenn du also eine Kiste über den Boden schiebst, dann braucht es eine Kraft senkrecht zum Boden, die sogenannte Normalkraft, die die Gewichtskraft kompensiert. Da hier also die Voraussetzung, dass es eine Normalkraft gegeben muss, erfüllt ist, wirkt auch eine Reibkraft zwischen Kiste und Boden, wenn du versuchst, sie in Bewegung zu setzen oder die Kiste verschiebst.
Wenn du die Kiste genau an einer Wand entlang schiebst, wirkt zwischen Wand und Kiste keine Reibkraft, solange du mit deiner Hand die Kraft exakt parallel zur Wand auf die Kiste aufbringst. Es gibt ja schlicht und einfach keine Kraft, die senkrecht zur Wand wirkt. Und wo keine Normalkraft, da auch keine Reibkraft.

Normalkraft als Voraussetzung für das Auftreten von Reibung

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Normalkraft_als_Voraussetzung_fuer_das%20Auftreten_von_Reibung.png

Tja, und wie ist das jetzt mit der Fortbewegung im Raumschiff im Weltall? Wieso kann sich die Besatzung der Enterprise gehend fortbewegen? Und wieso geht das auf der ISS nicht? Mehr dazu im Arbeitsblatt.

Kommen wir nochmal zu dem Punkt zurück, dass du auf einen Gegenstand eine Kraft ausüben kannst, ohne dass er sich bewegt. Je nachdem, wie feinmotorisch du unterwegs bist: Schnapp dir einfach mal einen leichten bis mittelschweren Gegenstand auf einem Tisch und probiere aus, wie doll du mit deinem Zeigefinger dagegendrücken kannst, bevor er anfängt sich zu bewegen. Und jetzt bleibst du mit der Kraft, die du aufbringst gerade unter dieser Grenze.
Merk dir, wie sich die Kraft anfühlt, die du gerade aufbringst. Wenn du jetzt den Gegenstand in Bewegung bringen willst, musst du ein bisschen mehr Kraft aufbringen. Und danach ist die Kraft sogar ein bisschen geringer, wenn du den Gegenstand mit konstanter Geschwindigkeit über den Tisch schiebst, oder?

Der Grund dafür, dass du eine Mindestkraft aufbringen musst, bevor sich der Gegenstand in Bewegung setzt, liegt darin, dass die beiden berührenden Oberflächen nicht glatt sind.
Selbst ein Glasbecher und ein geschliffener Holztisch, deren Oberfläche mit dem bloßen Auge sehr glatt wirken, sind es auf mikroskopischer Ebene nicht. Die Oberflächen sind rauh und die Spitzen, die sich auf beiden Oberflächen befinden, sind ineinandergeschoben und verhaken sich ein wenig.

Anschieben eines Glases auf einem Tisch

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Anschieben_eines_Glases_auf_einem_Tisch.png

Erst, wenn die Kraft, die du aufbringst, so groß ist, dass sich diese Spitzen voneinander lösen, setzt sich der Glasbecher im Bild in Bewegung. Und wenn die Spitzen erstmal voneinander getrennt sind und Bewegung vorliegt, schieben sie sich auch nicht wieder vollständig ineinander. Deswegen nimmt ist die Kraft, die du brauchst, um den Gegenstand mit konstanter Geschwindigkeit über den Tisch zu schieben, auch ein wenig geringer, als die Losbrechkraft.
Wenn der Tisch jetzt wieder noch feucht wäre, wäre es für die Spitzen einfacher, sich voneinander zu trennen. Die Losbrechtkraft wäre also geringer, als bei einer trockenen Oberfläche.

Und wie beschreibt man das jetzt alles?

Wenn du jetzt denkst: "Puuh, das sind ja ganz schön viele Phänomene, die es bei Reibung gibt. Das alles soll ich mathematisch beschreiben können?" Ja, ganz genau das. Und du wirst sehen, es ist eigentlich ganz einfach und vor allem logisch. Wie immer fangen wir mit dem an, was du schon kennst.
Stell dir also als erstes noch einmal vor, dass du auf einen Gegenstand eine beliebige Kraft aufbringst, deren Größe so ist, dass sich der Gegenstand nicht bewegt. Der Gegenstand befindet sich dann im Gleichgewicht. Das bedeutet, dass du alles anwenden kannst, was du bisher gelernt hast, da ja noch gar nichts neu ist: Freischneiden und Gleichgewichtsbedingungen aufstellen. Das machen wir doch einfach mal für ein Objekt mit der Masse \( m \). Zeichne als erstes das Freikörperbild für den Fall, dass nur die Gewichtskraft wirkt, du also noch gar nicht mit deinem Finger dagegendrückst. Im zweiten Fall kommt dann zusätzlich noch die Kraft \( F_{\mathrm{Finger}} \), die durch deinen Finger auf den Gegenstand ausgeübt wird, dazu.

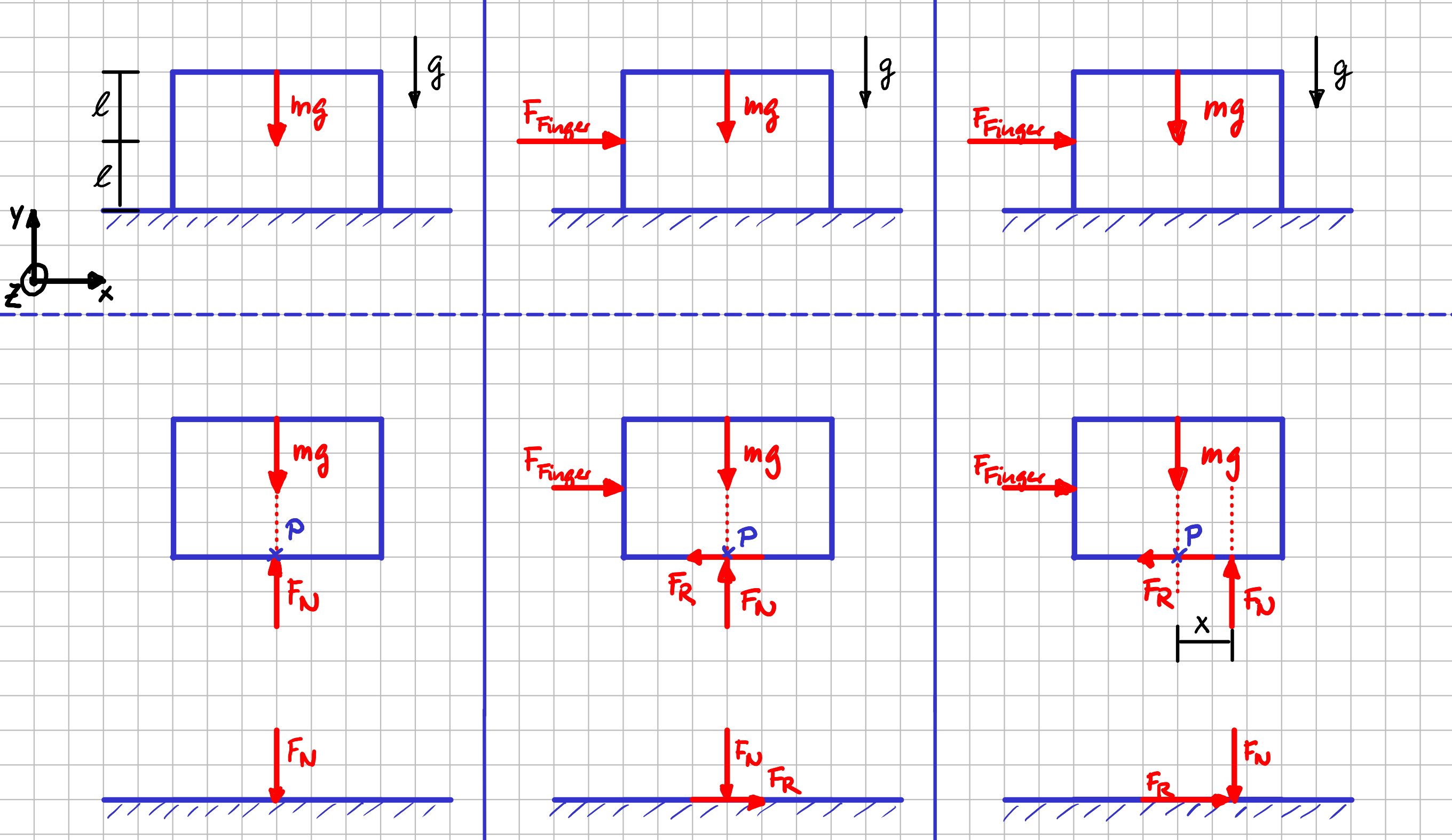
System und zwei Varianten für das Freikörperbild

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/System_und_zwei_Varianten_fuer_das_Freikoerperbild.png

Und? Wie sehen deine beiden Freikörperbilder aus? Ich habe die Normalkraft mit \( F_N \) und die Reibkraft mit \( F_R \) bezeichnet. Beim linken Freikörperbild \( - \) ohne Belastung durch die Fingerkraft \( - \) sind wir uns bestimmt einig. Aber welches Freikörperbild ist korrekt, wenn auch die Kraft durch deinen Finger auf den Gegenstand wirkt? Ist es das mittlere Freikörperbild? Oder das rechte? Oder noch eine andere Variante? Wenn du nicht gleich eine klare Antwort hast, stell doch einfach mal für alle drei Varianten die Gleichgewichtsbedingungen auf.

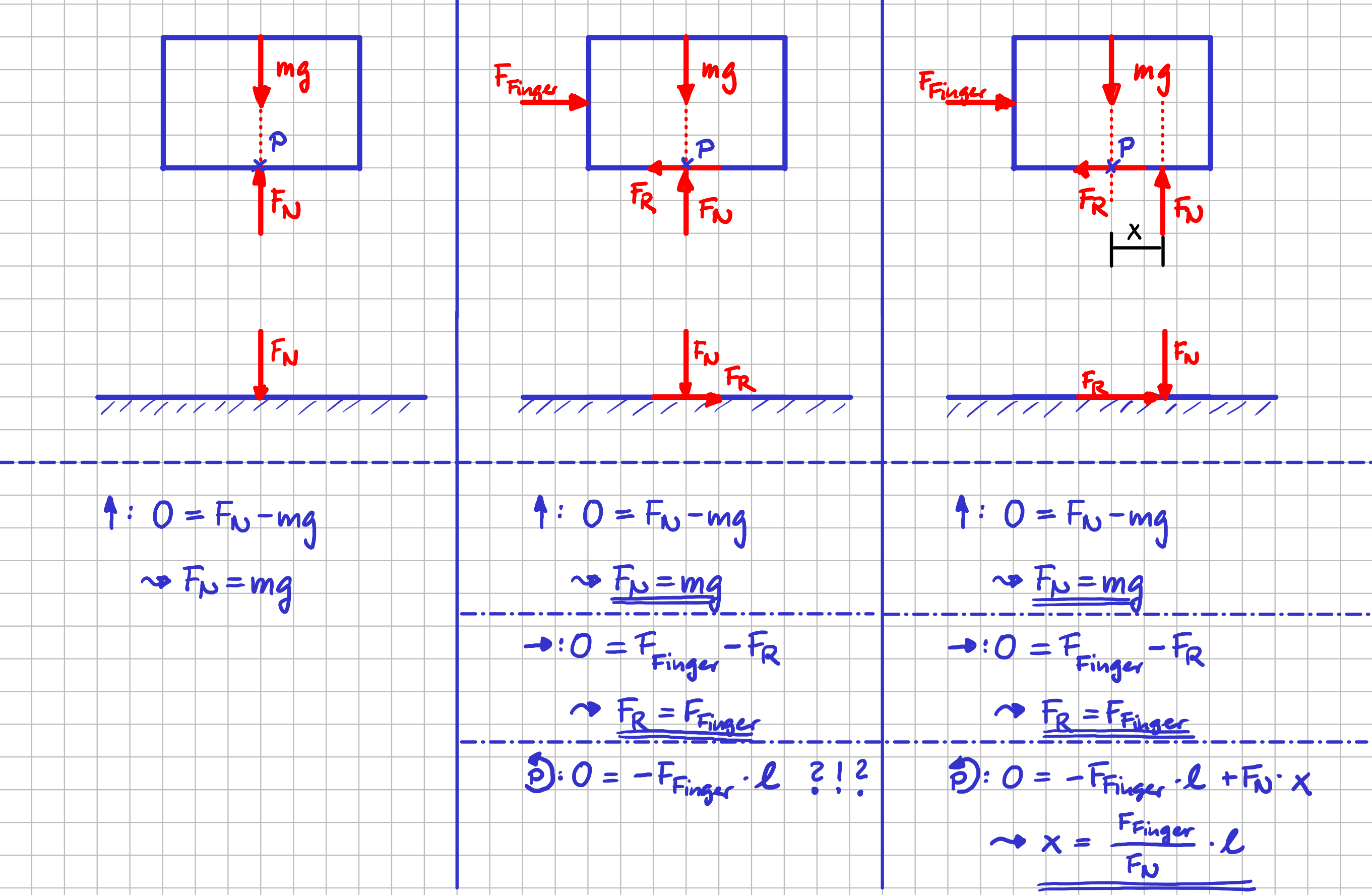
Gleichgewichtsbedingungen

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Gleichgewichtsbedingungen.png

In dem Fall, in dem nur die Gewichtskraft angreift, ist alles klar, oder? Zwischen Kiste und Boden wirkt als Reaktionskraft nur die Normalkraft \( F_N \) und ihr Betrag ist genauso groß wie die Gewichtskraft.
Schauen wir uns die Gleichgewichtsbedingungen für die beiden Varianten, in denen die Fingerkraft auch mit angreift, mal im Detail an.
\( y \)-Richtung
Auch hier gilt in beiden Fällen, dass die Normalkraft \( F_N \) der Gewichtskraft \( mg \) entgegenwirkt und der Betrag der Normalkraft genauso groß ist, wie die Gewichtskraft.
\( x \)-Richtung
Aus dem Kräftegleichgewicht in \( x \)-Richtung folgt, dass Fingerkraft \( F_{\mathrm{Finger}} \) und Reibkraft \( F_R \) entgegengesetzt gerichtet ist. Außerdem sind sie beide vom Betrag her gleich groß. Hier gibt es also auch keinen Unterschied.
\( z \)-Richtung
Beim Momentengleichgewicht um die \( z \)-Achse im Bezugspunkt \( P \) bekommst du unterschiedliche Ergebnisse. Im mittleren Fall müsste entweder die durch den Finger aufgebrachte Kraft oder die Länge \( \ell \) Null sein. Mmh, das klingt irgendwie komisch bzw. schlicht und einfach falsch. Weder die Kraft och die Länge sind Null.
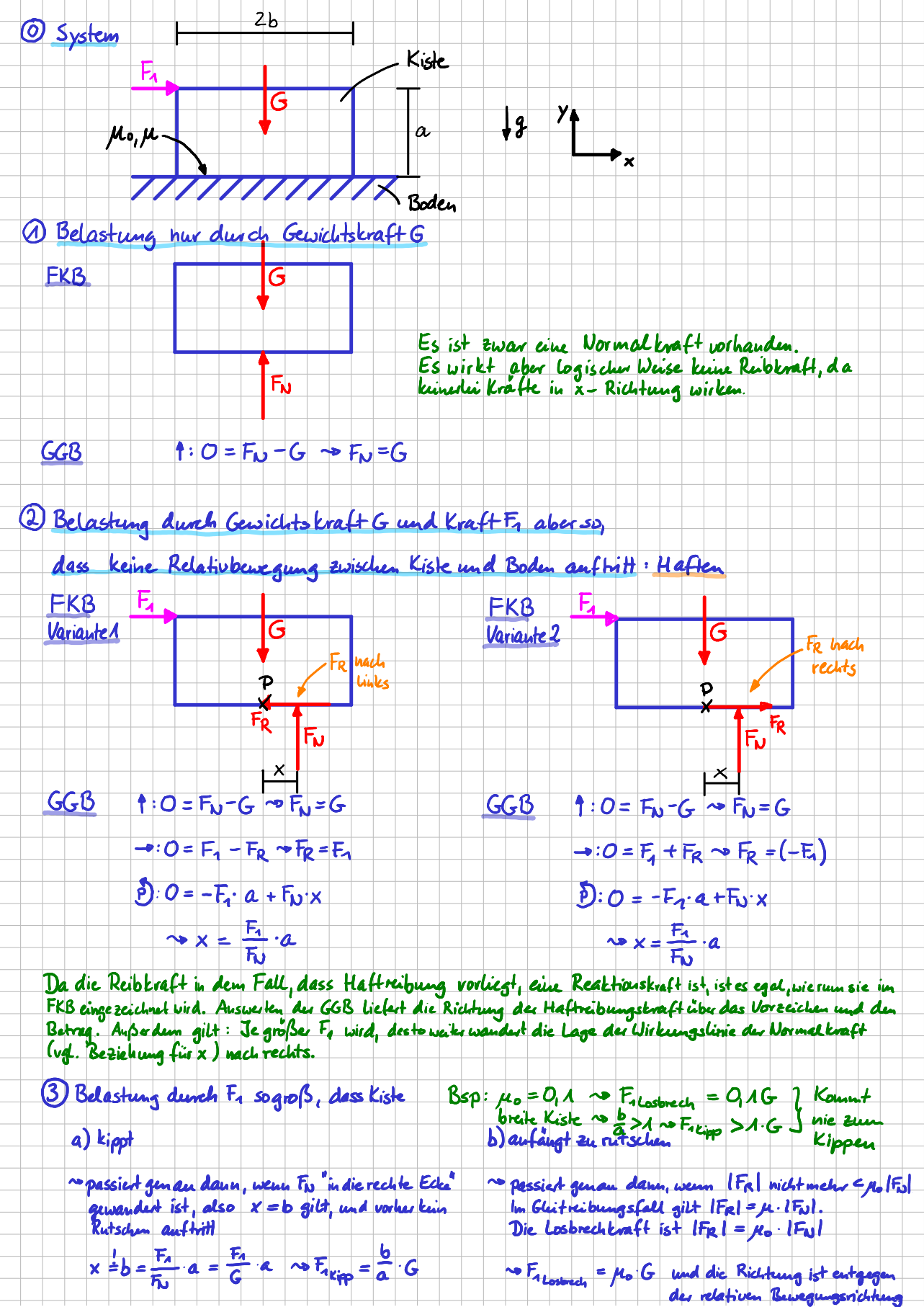
Bei der rechten Variante, in der die Normalkraft nicht im Punkt \( P \), sondern rechts davon angreift, kannst du über das Momentengleichgewicht bestimmen, wie groß der Abstand \( x \) der Wirkungslinie der Normalkraft vom Punkt \( P \) sein muss, damit das Momentengleichgewicht erfüllt ist. Das sieht alles sehr vernünftig aus!

Fazit:

Das mittlere Freikörperbild ist falsch.
Nur durch Anwenden dessen, was du bereits kennst (Freischneiden und Gleichgewichtsbedingungen aufstellen), hast du hergeleitet, dass der Angriffspunkt der Normalkraft davon abhängt, wie groß die vom Finger aufgebrachte Kraft ist: Je größer die Kraft ist, desto größer ist \( x \).

Irgendwie cool, oder? So lange Haftreibung vorliegt \( - \)genau das haben wir ja angenommen, da die Fingerkraft so klein sein soll, dass sich die Kiste (noch) nicht bewegt\( - \) ist gar nichts neu: Du kannst die Reibkraft wie eine Lagerkraft behandeln und bestimmst ihre Größe und ihre Richtung durch Auswerten der Gleichgewichtsbedingungen. Und wo die Wirkungslinie der Normalkraft langlaufen muss, bekommst du auch gleich noch aus den Gleichgewichtsbedingungen heraus.

Und wenn du jetzt noch einen kleinen Schritt weiterdenkst: Du kannst ja nach und nach die Fingerkraft, die du aufbringst, immer weiter erhöhen. Wenn wir annehmen, dass die Kiste dabei die ganze Zeit haftet, also nicht anfängt zu rutschen, dann würde \( x \) immer größer werden, was bedeutet, dass der der Angriffspunkt der Normalkraft immer weiter nach rechts wandert. Und wenn jetzt der Angriffspunkt der Normalkraft in der Ecke, also bei \( x=\frac{3}{2}\ell \) angekommen ist? Was passiert dann?

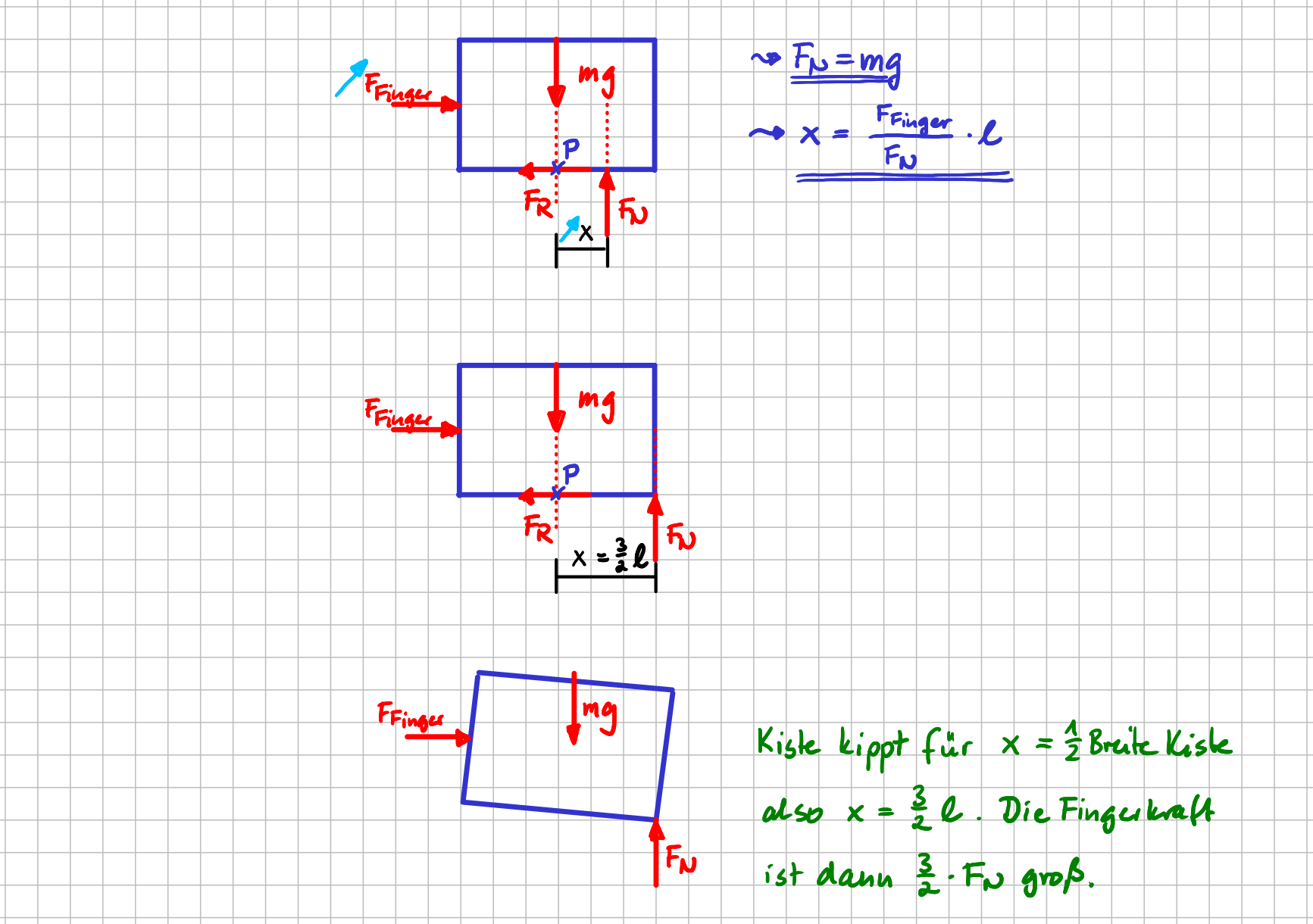
Bedingung dafür, dass die Kiste kippt

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Bedingungen_dafuer_dass_eine_Kiste_kippt.png

Dann beginnt die Kiste zu kippen. Probier das mal mit einem Umzugskarton oder auch mit einem Küchenstuhl aus. Kleiner Tipp: Wenn dein Versuchsobjekt erst anfängt zu rutschen, bevor es kippt, dann kannst du die eine Ecke auch einfach festhalten oder irgendwas darunterlegen, so dass der Kontakt zwischen Objekt und Boden möglichst rauh ist.

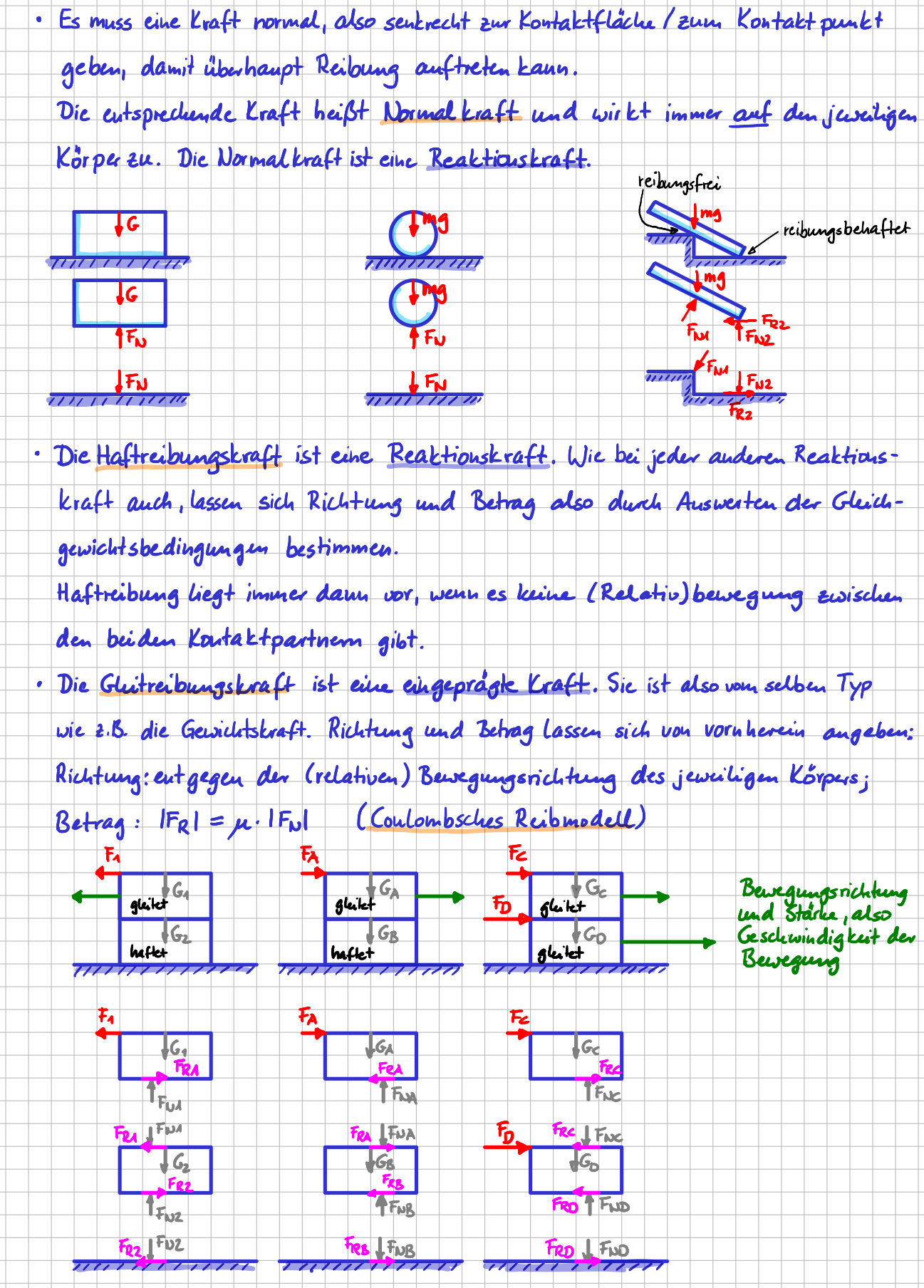
Du musst zugeben, dass ist fast schon ein langweilig einfaches Experiment. Und gerade deshalb kannst du schon unglaublich viel über die Reibkraft lernen.

Die Richtung der Normalkraft ist immer senkrecht zur Oberfläche. Die Richtung der Reibkraft ist wiederum senkrecht zur Richtung der Normalkraft.
So lange keine relative Bewegung zwischen zwei Körpern vorliegt, ist die Reibkraft wie eine Reaktionskraft in einem Lager. Ihre Richtung und ihr Betrag lässt sich „wie immer“ aus den Gleichgewichtsbedingungen berechnen. Man sagt „Es liegt Haftreibung vor.“. Und im Fall der Haftreibung ist die Reibkraft vom Typ „Reaktionskraft“.
Bei der Normalkraft ist von vorneherein immer physikalisch klar, in welche Richtung sie wirkt: AUF die jeweiligen Körper zu. Es macht also Sinn, sie von vornherein auch in diese Richtung im Freikörperbild einzuzeichnen.
Die Lage der Wirkungslinie der Normalkraft bei einem flächigen Kontakt, so wie wir ihn in unserem Beispiel mit der Kiste haben, ist so, dass das System im Gleichgewicht ist. In unserem Beispiel bedeutet das, dass die Wirkungslinie rechts von der Mittellinie der Kiste liegt. Die genaue Position lässt sich aus dem Momentengleichgewicht bestimmen.
Kippen tritt immer dann auf, wenn die Normalkraft aufgrund der Art und Weise, wie die anderen äußeren Belastungen wirken, in eine der Ecken des Objektes 'wandert'

Bleiben noch (mindestens) zwei Fragen: Wann kommt es denn jetzt eigentlich zum Rutschen und wie berücksichtigt man, dass es eine Grenzreibungskraft gibt, die sogar ein bisschen höher ist, als die Reibkraft, die vorliegt, wenn ein Körper rutscht? Wenn es zu einer Bewegung zwischen zwei Körpern kommt, dann ...... häääää, wir sind doch in der Statik. Da bewegt sich doch gar nichts. Stimmt. Aber Ingenieure lieben es, in Grenzfällen zu denken. Und bis zu dem Punkt, in dem ein Körper gerade anfängt, sich zu bewegen, können wir sehr wohl mit Argumenten der Statik hantieren. Also, ..... wenn es zu einer Bewegung zwischen zwei Körpern kommt, dann ändert sich etwas Fundamentales in Bezug auf die Reibkraft. Aber mal langsam und Schritt für Schritt: Erinnern wir uns noch einmal kurz daran, dass es drei Informationen braucht, um eine Kraft eindeutig zu beschreiben

die Richtung,
den Betrag und
die Lage der Wirkungslinie.

Körper befinden sich in Ruhe: Es liegt Haftreibung vor

Im Fall, dass Haftreibung vorliegt, ist die Richtung der Normalkraft von vornherein physikalisch vorgegeben (auf den jeweiligen Körper zu). Betrag und Lage der Wirkungslinie lassen sich aus den Gleichgewichtsbedingungen ermitteln. Für die Reibkraft ist im Fall der Haftreibung die Lage der Wirkungslinie direkt bekannt (liegt in der Kontaktfläche), Richtung und Betrag lassen sich wie bei jeder anderen Reaktionskraft auch aus den Gleichgewichtsbedingungen bestimmen.

Es liegt eine Relativbewegung zwischen den beiden Körpern vor: Es liegt Gleitreibung vor

Jetzt aber: Wenn es Bewegung zwischen zwei Körpern auftritt, sie also aufeinander gleiten, ändert sich bei der Normalkraft gar nichts: die Richtung der Normalkraft ist von vornherein physikalisch vorgegeben (auf den jeweiligen Körper zu). Betrag und Lage der Wirkungslinie lassen sich aus den Gleichgewichtsbedingungen ermitteln. Bei der Reibkraft ist dei Lage der Wirkungslinie immer noch direkt bekannt (liegt in der Kontaktfläche). Aber sonst ist alles anders: Die Richtung ist im Fall der Gleitreibung bekannt, nämlich entgegen der Bewegungsrichtung. Und aus Versuchen kann man zeigen, dass der Betrag der Reibkraft in vielen Fällen proportional zur Normalkraft ist. Die Gleitreibungskraft ist also vom Typ "eingeprägte Kraft", da Richtung, Betrag und Lage der Wikrungslinie von vornherein bekannt sind. Charles Augustin de Coulomb hat neben vielen anderen Wissenschaftlern umfangreiche Versuche zum Thema Reibung durchgeführt. Nach ihm ist das einfachste Reibmodell, die Coulombsche Reibung benannt: \( |\vec{F}_R| \propto |\vec{F}_N| \) also \( F_R \propto F_N\) im Fall der Gleitreibung. Die Proportionalitätskonstante wird üblicherweise mit \(\boldsymbol{\mu}\) bezeichnet und heißt Gleitreibungskoeffizient. Der Gleitrebungskoeffizient \( \mu \) wird experimentell ermittelt und berücksichtigt z.B. die Materialpaarung und die Oberflächenbeschaffenheit. Typische Werte für Stahl liegen bei

Paarung	Gleitreibungskoeffizient \( \mu \)
Stahl - Stahl	0,1
Stahl - Beton	0,2
Stahl - Eis	0,01

Im Fall der Gleitreibung gilt also

Richtung entgegen der Bewegungsrichtung
\( |\vec{F}_R| \propto |\vec{F}_N| \rightarrow |\vec{F}_R| = \mu \cdot |\vec{F}_N| \)
Lage: in der Berührfläche

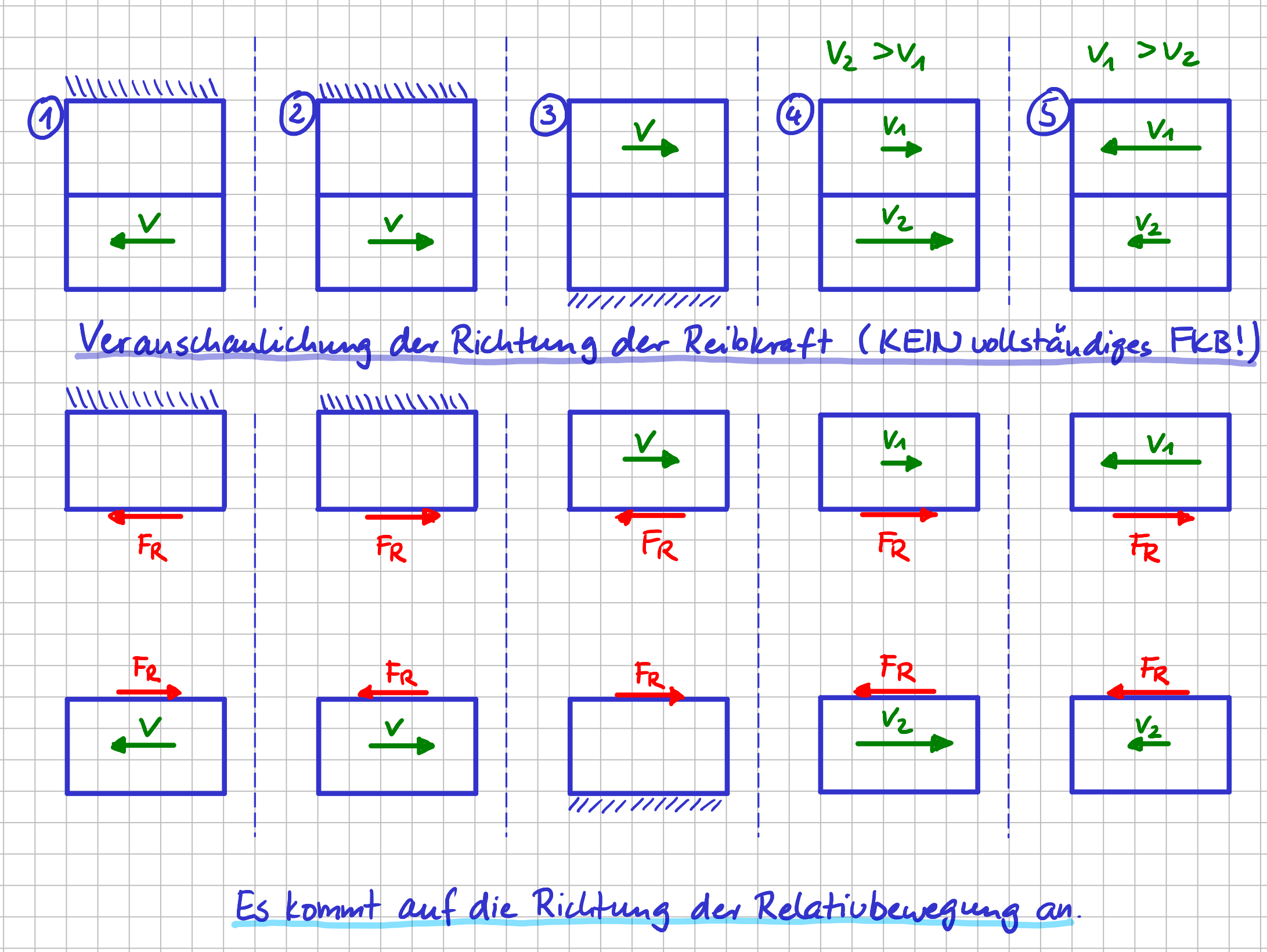
Richtung der Reibkraft für verschiedene Fälle

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Richtung_der_Reibkraft_fuer_verschiedene_Faelle.png

Und wie kannst du nun feststellen, ob schon Gleitreibung vorliegt, oder ob noch Haftreibung vorherrscht? Ganz einfach: So lange \( |\vec{F}_R| < \mu \cdot |\vec{F}_N| \) liegt noch Haftreibung vor. Wir haben ja schon selbst beim Schieben des Objektes bemerkt, dass die Losbrechkraft ein bischen größer ist als die Kraft, die zum anschließenden Schieben erforderlich ist. Deshalb wird die Bedingung, bis wann Haftreibung vorliegt, meist so formuliert \( |\vec{F}_R| < \mu_0 \cdot |\vec{F}_N| \). \( \boldsymbol\mu_0 \) ist der sogenannte Haftreibungskoeffizient. Er ist vom Zahlenwert her ein bisschen größer als der Gleitreibungskoeffizient \( \mu \): \( \mu_0 < \mu\).

Paarung	Gleitreibungskoeffizient \(\boldsymbol\mu \)	Haftreibungskoeffizient \( \boldsymbol\mu_0 \)
Stahl - Stahl	0,1	0,2
Stahl - Beton	0,2	0,35
Stahl - Eis	0,01	0,03

Und um es nochmal klar zu sagen: Du kannst mit Methoden der Statik nur bis zum Grenzfall der beginnenden Bewegung, also der beginnenden Gleitreibung rechnen. Aber das ist ja schon sehr viel. So kannst du z.B. schon die maximal zulässige äußere Kraft berechnen, ab der sich ein Gegenstand in Bewegung setzt. Wie sich der Gegenstand dann bewegt bzw. sich diese Bewegung dann beschreiben lässt, ist Gegenstand des Teilgebiets "Dynamik".

Wie geht man jetzt konkret bei Aufgaben vor?

Für das Vorgehen bei Aufgaben gibt es zwei verschiedene Fälle.

Fall 1: Es ist vorab klar, ob Gleitreibung oder Haftreibung vorliegt

Liegt Haftreibung vor, behandelst du die Reibkraft wie jede andere Reaktionskraft auch. Durch Auswerten der Gleichgewichtsbedingungen bekommst du Betrag und Richtung heraus.
Liegt Gleitreibung vor, zeichnest du die Richtung der Reibkraft entgegen der Bewegungsrichtung am Körper ein und berechnest den Betrag über \( F_R=\mu \cdot F_N \).

Fall 2: Es ist vorab nicht klar, ob Haft- oder Gleitreibung vorliegt

Schritt 1: Du nimmst an, dass Haftreibung vorliegt, behandelst die Reibkraft also als Reaktionskraft und rechnest ihren Betrag und ihre Richtung über das Auswerten der Gleichgewichtsbedingungen aus.

Schritt 2: Anschließend prüfst du, ob deine Annahme korrekt war, in dem du den Wert, den du für \( F_R \) erhalten hast, in die Ungleichung \( |F_R| < \mu_0 \cdot |F_N| \) einsetzt.

Variante 1) Ist die Ungleichung erfüllt, war deine Annahme korrekt. Im System liegt Haftreibung vor.

Variante 2) Ist die Ungleichung nicht erfüllt, war die Annahme, dass Haftreibung vorliegt, nicht korrekt. Es liegt also keine Haftreibung, sondern Gleitreibung vor. Im Fall von Gleitreibung wissen wir was für Betrag und Richtung gilt. Für den Betrag gilt \( |F_R|= \mu \cdot |F_N|\). Außerdem ist die Richtung der Reibkraft an jedem Körper entgegen der relativen Bewegungsrichtung.

Zusammenfassung - Das Wichtigste in Kürze

Die Reibkraft ist eine Kraft, die je nach Bedingungen im System in zwei unterschiedlichen 'Arten' auftritt: als Haftreibung und als Gleitreibung.

\( \boldsymbol\mu \) ist der Gleitreibungskoeffizient und \( \boldsymbol\mu_0 \) ist der Haftreibungskoeffizient.

Haftreibung und Gleitreibung und was sie charakterisiert

Haftreibung und Gleitreibung und was sie charakterisiert

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Haftreibungs_und_Gleitreibungskraft_und_was_sie_charakterisiert.png

Beispiel, bei dem alle Reibungszenarien auftreten können

Beispiel, in dem alle Reibungsszenarien auftreten können

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Beispiel_alle_Reibungsszenarien.png

Vorgehen bei Reibungsaufgaben

Wenn nicht von vornherein bekannt ist, ob Haft- oder Gleitreibung vorliegt, rechnest du als erstes so, als ob Haftreibung vorliegen würde. Wenn du denBetrag für \( F_R \) durch Auswerten der Gleichgewichtsbedingungen bestimmt hast, prüfst du, ob deine Annahme, das Haftreibung vorliegt, korrekt war. Gilt \( |F_R| < \mu_0 \cdot |F_N| \) liegt in der Tat Haftreibung vor. Wenn diese Bedingung nicht erfüllt ist, liegt Gleitreibung vor. Der durch Auswerten der Gleichgewichtsbedingungen erhaltene Wert für \( F_R \) ist nicht korrekt, denn es gilt \( |F_R| = \mu \cdot |F_N| \) und die Richtung der Gleitreibungskraft ist entgegen der relativen Bewegungsrichtung.

Arbeitsblatt - Teste dein Wissen

Reibung: Bekannte oder schon Freundin?

Bremse mit Reibmechanismus

Wilmas Mechanikwelt

Verflixte Reibung Ich liebe Eis. Joghurt-Feige und Joghurt-Heidelbeere mag ich besonders gerne. Natürlich schmeckt Eis besser, wenn es nicht gerade regnet. Aber Eis geht ja eigentlich immer. Was total doof ist: Meine 5-Meter-Schleppleine wickelt sich immer um die Tischbeine und Stuhlbeine. Das freie Leinenende liegt einfach auf dem Boden. Kannst du erklären, warum ich irgendwann so doll ziehen kann, wie ich will? Ich komme einfach nicht mehr von der Stelle. Was hat das mit Reibung zu tun? Kleiner Tipp: Es hat nicht nur mit Seilreibung zu tun. "Normale" Reibung spielt auch noch eine Rolle. Wenn du eine Lösung zu dem Rätsel hast, schreib gerne an diese Emailadresse. Dann schreibe ich deine Lösung hier mit rein. Bin schon sehr gespannt auf deine Ideen.

Verfixte Reibung

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2170/Verflixte_Reibung.png