Kraft
Kraft
3. Verschiedene Kraftarten ganz nah
3.2. Streckenlast = Linienlast
Streckenlast = Linienlast
Eine Streckenlast, die auch als Linienkraft bezeichnet
wird, ist zwar eine Idealisierung, die in realen Systemen kaum
vorkommt. Bei der Modellierung von räumlichen Systemen als ebene Systeme
ist sie aber eine sehr häufig verwendete Lastart. Sie wird z.B. dafür
verwendet, um das Eigengewicht von Komponenten mit seiner Verteilung zu
berücksichtigen. Das Eigengewicht ist ja in ganz vielen Anwendungen relevant, wie zum Beispiel bei Brücken und bei Dächern. Auch um flächige Lasten aus der Realität, wie z.B. Schneelasten, Windlasten, oder Auftriebslasten in zweidimensionalen Modellen zu berücksichtigen, kannst du die Streckenlast sehr gut verwenden. Es lohnt sich also, sich mit dieser Art von Belastung intensiver zu beschäftigen.
Aber der Reihe nach. Stell dir vor, du schneidest mit einem Messer z.B. Käse.
Wenn wir die Dicke der Schneide vernachlässigen, was sicherlich eine sehr plausible Näherung ist, dann ist die vom Messer auf den Käse wirkende Belastung eine Streckenlast.
Die Einheit ist "Kraft pro Länge" also z.B. \( \mathbf{\left[\frac{N}{m}\right]}. \)
Es ist also eine spezifische Größe, da sie auf die Länge bezogen ist.

Kraft zwischen der Schneide eines Messers und Käse als reales Beispiel für eine Streckenlast
Weitere Informationen
Charles Williams
CC BY 2.0
https://www.flickr.com/photos/99652207@N00/378503271
Für die mechanische und mathematische Darstellung werden üblicherweise folgende Bezeichnungen und Darstellungen verwendet:

Typische Bezeichnungen und Darstellungen im Zusammenhang mit Streckenlasten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Typische_Bezeichnungen_und_Darstellungen_Streckenlast.png
Schauen wir uns die Sache mit dem Eigengewicht eines Körpers, das über eine Streckenlast berücksichtigt werden kann, gleich mal genauer an.
Ein I-Träger, wie er auf dem Bild links zu sehen ist, wird in vielen bautechnischen Konstruktionen verwendet, z.B. in der Tragstruktur für eine Fabrikhalle.

I-Träger (links) und Verwendung in der Tragstruktur einer Fabrikhalle (rechts)
Weitere Informationen
Wir betrachten einen I-Träger mit den äußeren Abmessungen 200mm x 200mm aus Stahl und einer Stegbreite von 15mm bzw. 9mm. Er hat eine Masse von 63kg pro Meter Länge und damit eine Gewichtskraft von ca. 600N pro Meter.

Abmessungen und Gewichtskraft I-Träger
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Abmessungen_und_Gewichtskraft_I_Traeger.png
Wie wirkt es sich nun aus, wenn wir das Eigengewicht so eines Balkens in Form von Einzelkräften im Vergleich zu einer Streckenlast im Modell berücksichtigen? Dazu wollen wir uns ein Modell anschauen, bei dem ein Balken von 1m Länge am linken Ende mit einem Festlager und am rechten Ende mit einem Loslager gegenüber der Umgebung abgestützt ist.
Dieser Aufbau kann ein einem ebenen System abgebildet werden, da das Eigengewicht nur in einer Richtung wirkt, es also keinen räumlichen Belastungsfall gibt.
Das ebene System sieht dann so aus:
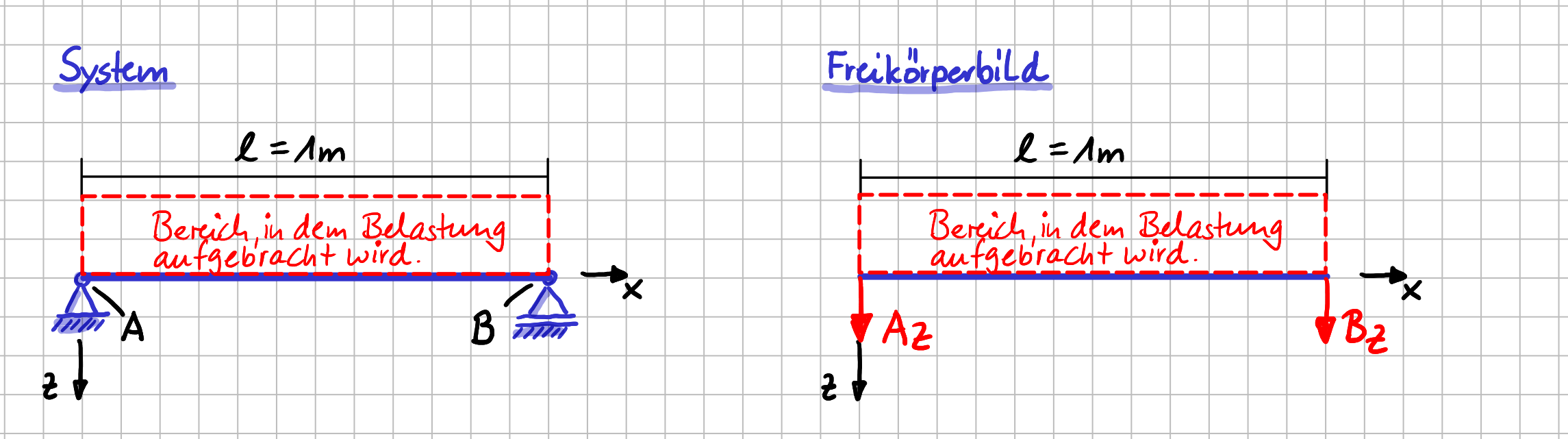
Ebenes Modell des Balkens mit Lagerung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Ebenes_Modell_des_Balkens_mit_Lagerung.png
Um das Eigengewicht von 600N zu berücksichtigen, hast du verschiedene Möglichkeiten. Du kannst eine Einzelkraft \( \vec{F}_1 \) mit einem Betrag von 600N aufbringen, Fall 1. Du kannst zwei Einzelkräfte \( \vec{F}_2 \) mit einem Betrag von je 300 N aufbringen, Fall 2. Du kannst drei Einzelkräfte mit einem Betrag von je 200 N aufbringen, Fall 3..... und so weiter. Oder du kannst eine konstante Streckenlast von 600\( \frac{\mathrm{N}}{\mathrm{m}} \) aufbringen, Fall 6.
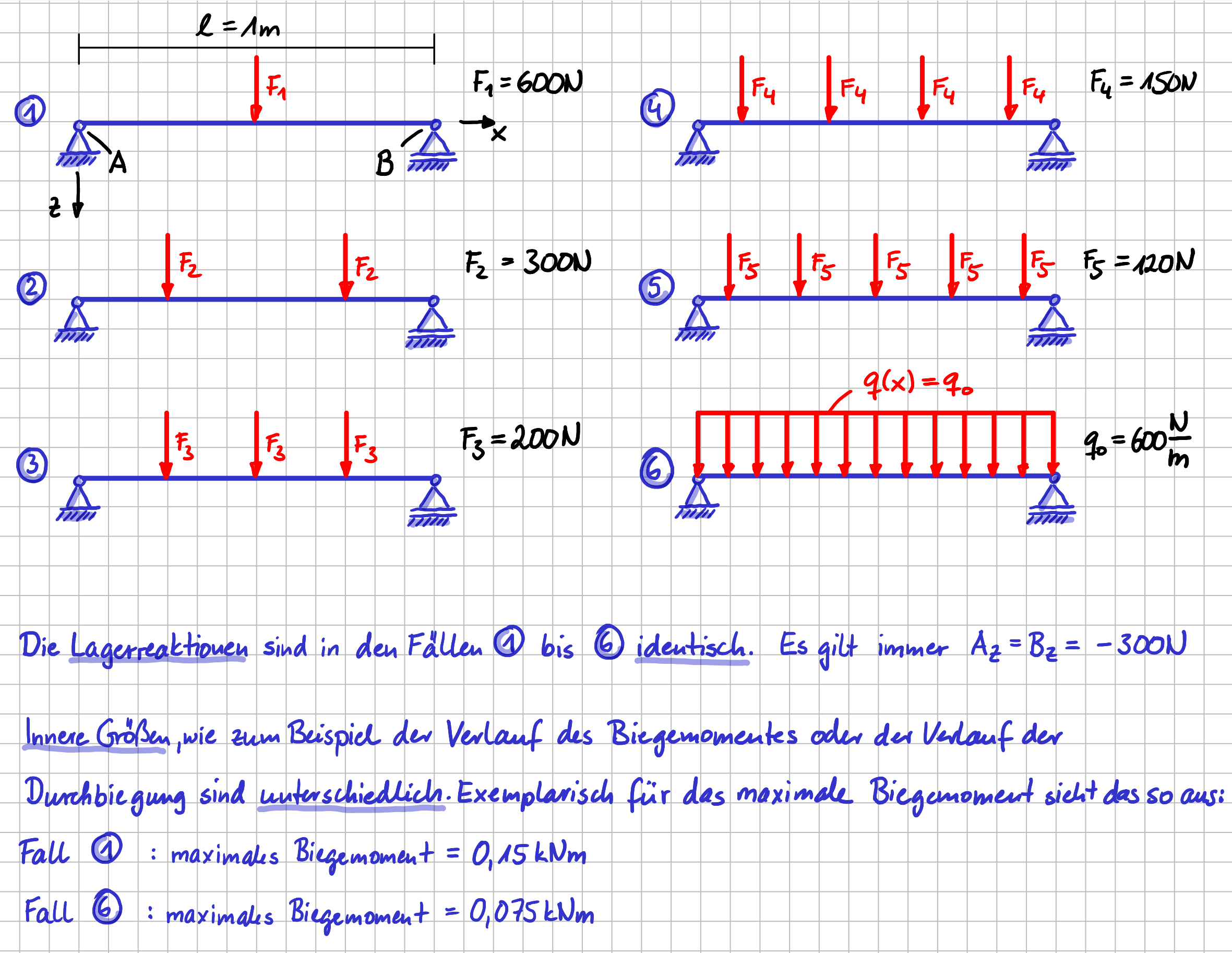
Verschiedenen Variante, um das Eigengewicht im Modell zu berücksichtigen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
Verschiedene_Varianten_um_Eigengewicht_im_Modell_zu_ber%C3%BCcksichtigen.png
Die Entscheidung darüber, wie genau du das Eigengewicht in deinem Modell berücksichtigen musst, hängt davon ab, was du untersuchen und berechnen willst. Die Werte der Lagerreaktionen \( A_z \) und \( B_z \) sind in allen sechs Fällen identisch. Bis du also nur an den Lagerreaktionen interessiert, reicht es aus, das Eigengewicht als Einzelkraft mit dem der Streckenlast entsprechenden resultierenden Größe zu berücksichtigen. Oder anders formuliert: Eine Streckenlast kann für die Berechnung der Lagerreaktionen zu einer äquivalenten Einzelkraft zusammengefasst werden.
Sobald du an inneren Größen interessiert bist, also z.B. wissen möchtest, wie stark sich der Balken durchbiegt oder wie groß das maximale Biegemoment ist, das im Balken auftritt, wird deine Berechnung umso genauer, je genauer du die Realität in deinem Modell abbildest. Und da das Eigengewicht des Balkens über seine gesamte Länge verteilt ist, bekommst du das genaueste Ergebnis für den Wert des maximalen Biegemoments, wenn du das Eigengewicht als Streckenlast berücksichtigst.
Wenn du dich mit mechanischen Systemen beschäftigst, wirst du immer wieder Streckenlasten \( q(x) \) zu einer äquivalenten Einzelkraft \( F_q \) zusammenfassen. Dieses Vorgehen ist immer dann hilfreich, wenn Lagerreaktionen bestimmt werden sollen, aber auch, wenn du den Verlauf von Schnittgrößen abschnittsweise bestimmst.
Deshalb wollen wir uns an dieser Stelle noch einmal genau anschauen, wie du von einer Streckenlast \( q(x) \) \( - \) egal wie einfach oder komplex sie ist \( - \) zur Einzelkraft \( F_q \) kommst.
Ganz allgemein ist eine Einzelkraft ja charakterisiert durch ... na, denk schnell selbst nach, bevor du weiterliest ... ok, ich helfe dir ein bisschen ... es sind drei typische Eigenschaften, die du angeben musst ...
- ...
- ...
- ...
- die Richtung
- den Angriffspunkt und
- den Betrag.
Die Richtung, der Betrag und der Angriffspunkt müssen so gewählt werden, dass sich die "Wirkung nach außen" nicht ändert. Mechanisch gesprochen bedeutet dies, dass die Auswertung der Gleichgewichtsbedingungen (Kräfte- und Momentengleichgewicht) für das System mit der Streckenlast und das System mit der äquivalenten Einzelkraft \( F_q \) auf dasselbe Ergebnis führen muss.
Die Richtung der Einzelkraft \( F_q \) ist identisch der Richtung von \( q(x) \). Warum sollte es anders sein?
Der Betrag von \( F_q \) entspricht der Fläche, die von \( q(x) \) überdeckt ist. Der Angriffspunkt ist der Schwerpunkt der Fläche, die von \( q(x) \) überdekct ist. Die Wirkungslinie von \( F_q \) muss also durch den Schwerpunkt genau dieser Fläche gehen.
Schauen wir uns das an drei Beispielen an.
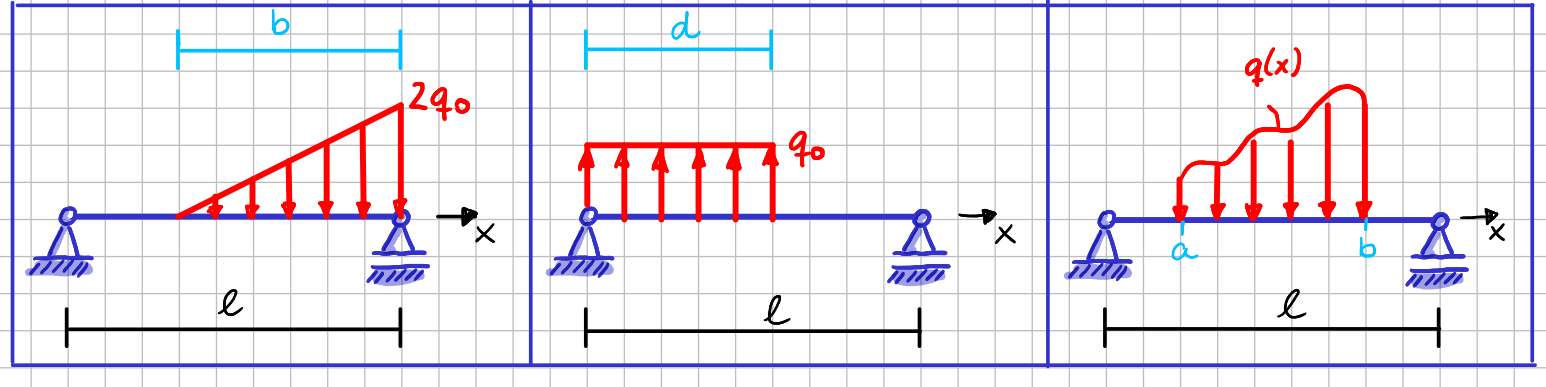
Drei verschiedene Verläufe für Streckenlasten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Drei_verschiedene_Verl%C3%A4ufe_fuer_Streckenlasten.png
Wenn du jetzt also die Anweisungen befolgst, kannst du die Lage der Wirkungslinien und die Richtung von \( F_q \) in allen drei Fällen gleich einzeichnen, oder?
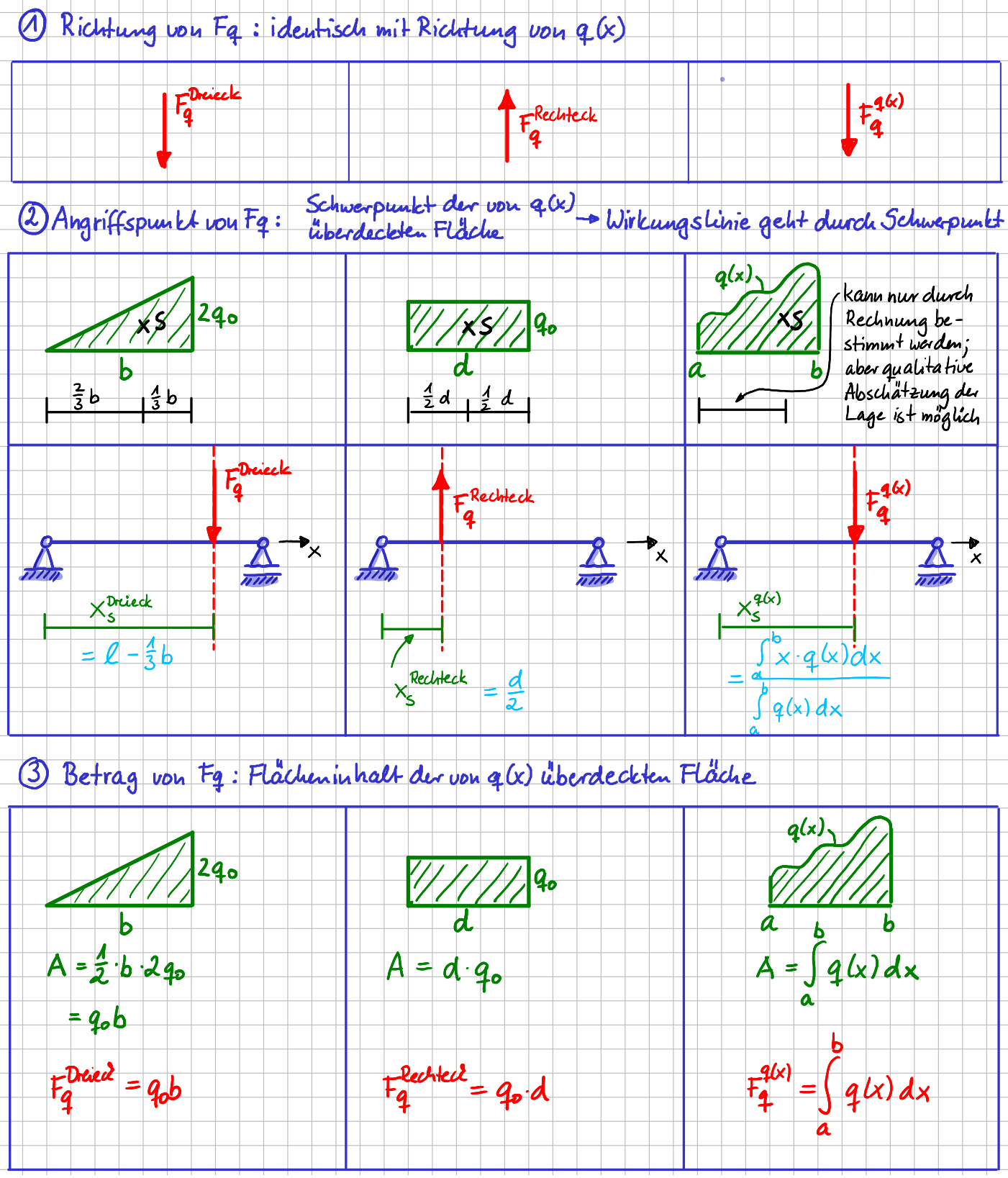
Bestimmung der äquivalenten Einzelkraft \(F_q\)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Bestimmung_der_aequivalenten_Einzelkraft.png
Damit hast du für alle drei Systeme die äquivalente Einzelkraft \(F_q\) bestimmt.
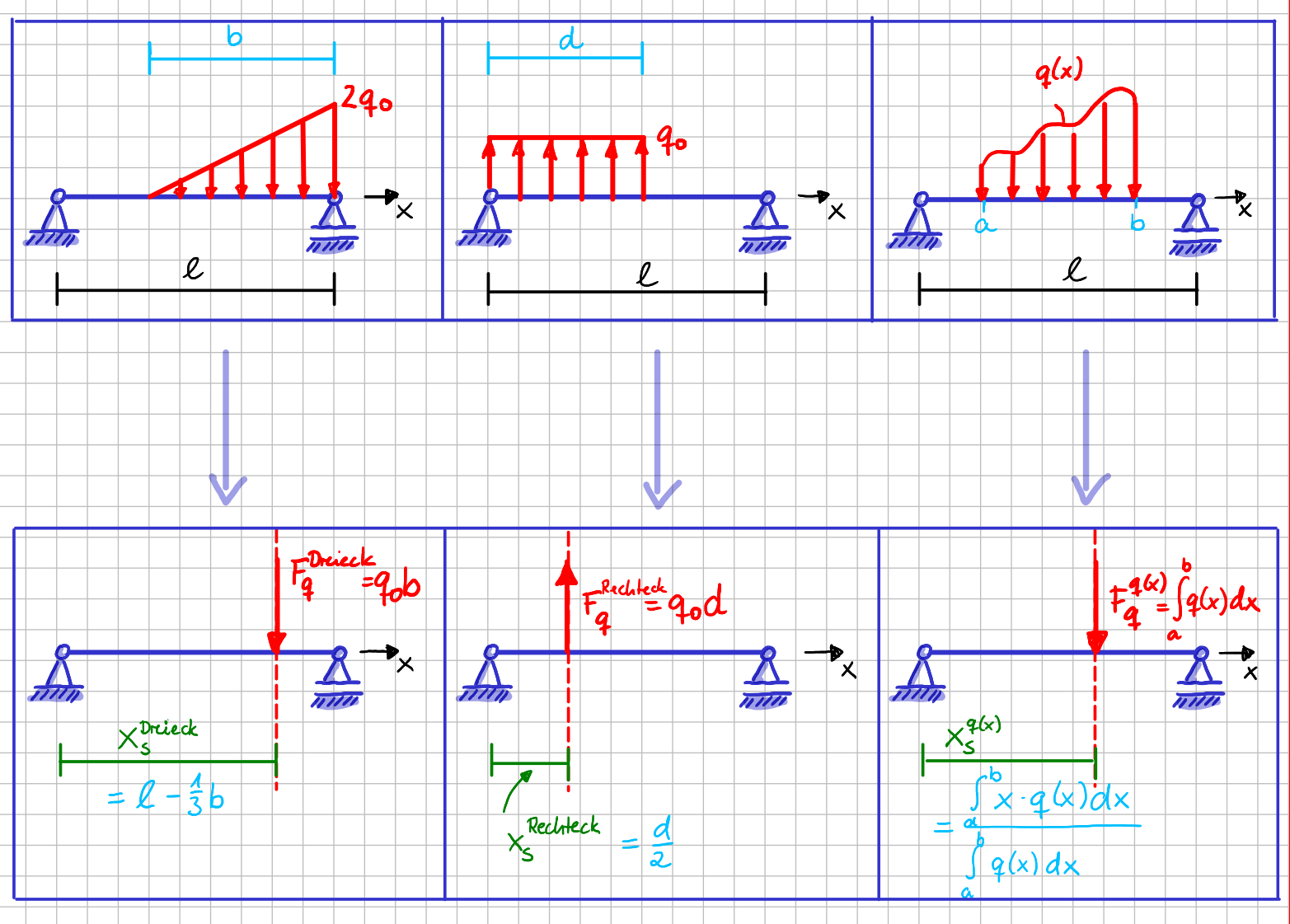
Ausgangssysteme und Ersatzsysteme mit äquivalenter Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Ausgangssysteme_und_Ersatzsysteme_mit_aequivalenter_Einzelkraft.png
Schauen wir nochmal genau auf die Fläche im Fall der rechteckförmigen Streckenlast. Eine Kantenlänge ist \( d \), also eine Länge, die z.B. in \( [\mathrm{m}] \) gegeben sein kann. Die andere Kantenlänge ist \( q_0 \), die z.B. in \( \left[\frac{\mathrm{N}}{\mathrm{m}}\right] \) gegeben sein kann. Das mag dich zunächst irritieren, da Flächen ja die Einheit "Länge \( ^2 \)" also z.B. \( [\mathrm{m}^2] \) haben. Unsere Fläche ist also keine Fläche im klassischen Sinn, was ja wiederum auch total Sinn macht, da wir ja sagen, dass die Streckenlastfläche dem Betrag der Kraft \( F_q \) entspricht. Und der Betrag einer Kraft wird ja bitteschön immer noch in \( [\mathrm{N}] \) angegeben. Wenn wir jetzt also die beiden Kantenlängen unserer Streckenlastfläche mit einander multiplizieren, so gilt für die Einheiten \( [\mathrm{m}] \cdot\left[\frac{\mathrm{N}}{\mathrm{m}}\right] = [\mathrm{N}] \). Die Dimension des Flächeninhalts der Streckenlastfläche ist also \( [\mathrm{N}] \). Und damit hat alles seine Richtigkeit.
Zusammenfassung - Das Wichtigste in Kürze
- die Richtung
\( \rightarrow \) dieselbe wie die der Streckenlast - die Lage der Wirkungslinie
\( \rightarrow \) geht durch den Schwerpunkt der von \( q(x) \) überdeckten Fläche - den Betrag
\( \rightarrow \) entspricht dem Flächeninhalt der von \( q(x) \) überdeckten Fläche
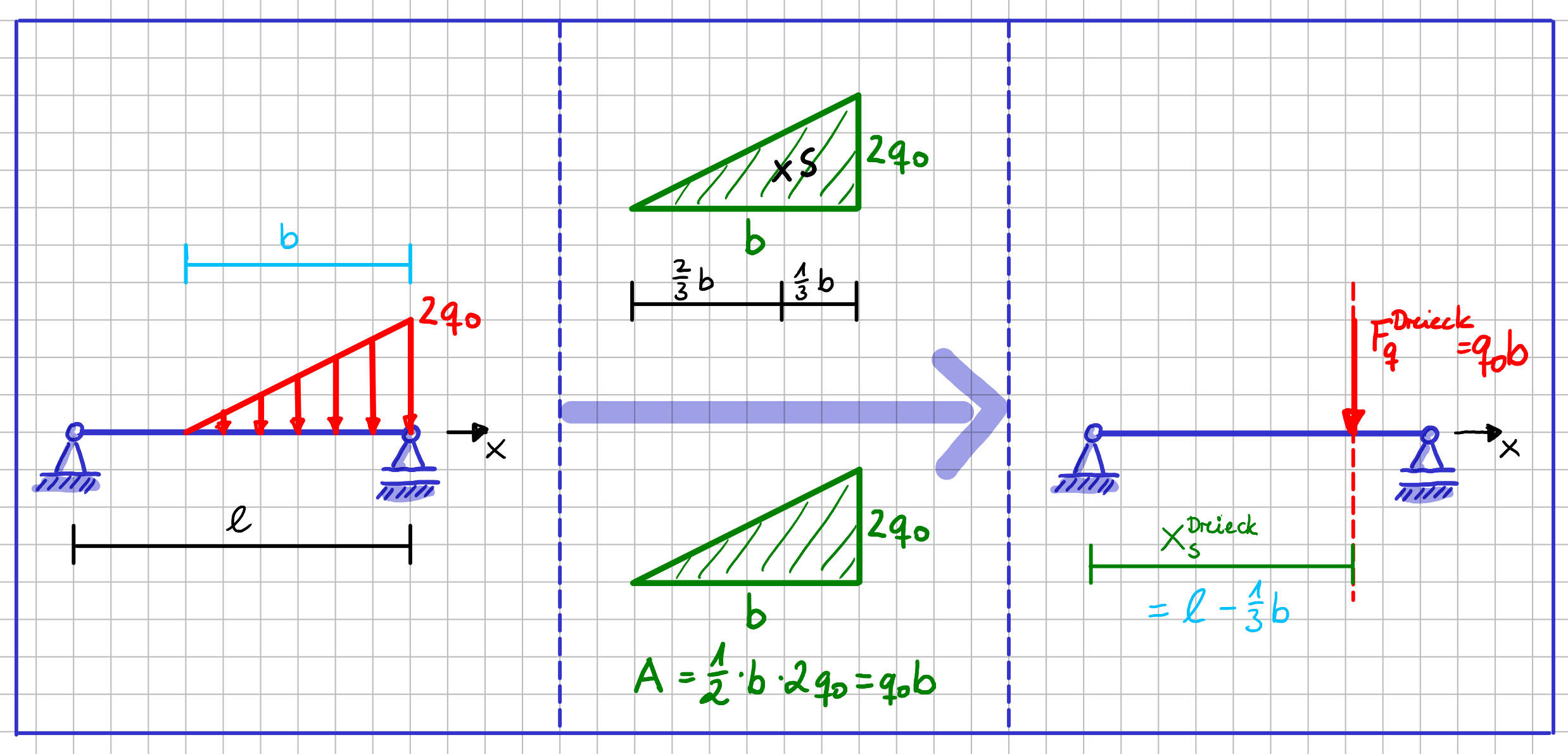
Ausgangssystem und Ersatzsystem mit äquivalenter Einzelkraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2168/Ausgangssystem_und_Ersatzsystem_mit_aequivalenter_Einzelkraft.png

