Ebenes und räumliches Kräftesystem

Wenn auf einen Körper mehrere Kräfte wirken, so nennt man all diese Kräfte zusammen Kräftesystem. 

In der Mechanik werden Kräftesysteme in Bezug auf ihre Dimension unterschieden:
es gibt ebene Kräftesysteme, oft als 2D-Systeme bezeichnet, und räumliche Kräftesysteme, oft als 3D-Systeme bezeichnet.

Gleich vorweg: Die Bezeichnungen "2D" und "3D" können irreführend sein: Sie suggerieren vielleicht, dass die Systeme dahingehend unterschieden werden, ob die betrachteten Körper und Elemente zweidimensional oder dreidimensional modelliert werden können; aber genau darum geht es eben nicht. Also: schau dir im Folgenden erst an, was mit "Dimension" im Kontext von Kräftesystemen in der Mechanik überhaupt gemeint ist. Dann entscheide selbst, welche Begriffe du verwendest, um Kräftesysteme zu charakterisieren. Mit "eben" und "räumlich" liegst du in jedem Fall immer auf der sicheren Seite.

Ebenes Kräftesystem

Ein ebenes Kräftesystem kannst du daran erkennen, dass die Wirkungslinien aller Kräfte in einer Ebene liegen. 

In den  beiden gezeigten Beispielen handelt es sich beide Male um einen räumlichen Körper.
Aber die Belastungen sind unterschiedlich:

• im linken System wirken die Kräfte alle in der \( xy- \)Ebene, d.h. also, dass ihre Wirkungslinien alle in der \( xy- \)Ebene liegen. Außerdem sind die Ortsvektoren der Kräfte alle in der \( xy- \)Ebene. Es handelt sich also um ein ebenes Kräftesystem.
• im rechten System lliegen die Wirkungslinien der Kräfte nicht mehr alle in einer Ebene. Zusätzlich wirken auch Kräfte in \( z- \)Richtung. Das ist also kein ebenes Kräftesystem mehr, sondern ein räumliches Kräftesystem.

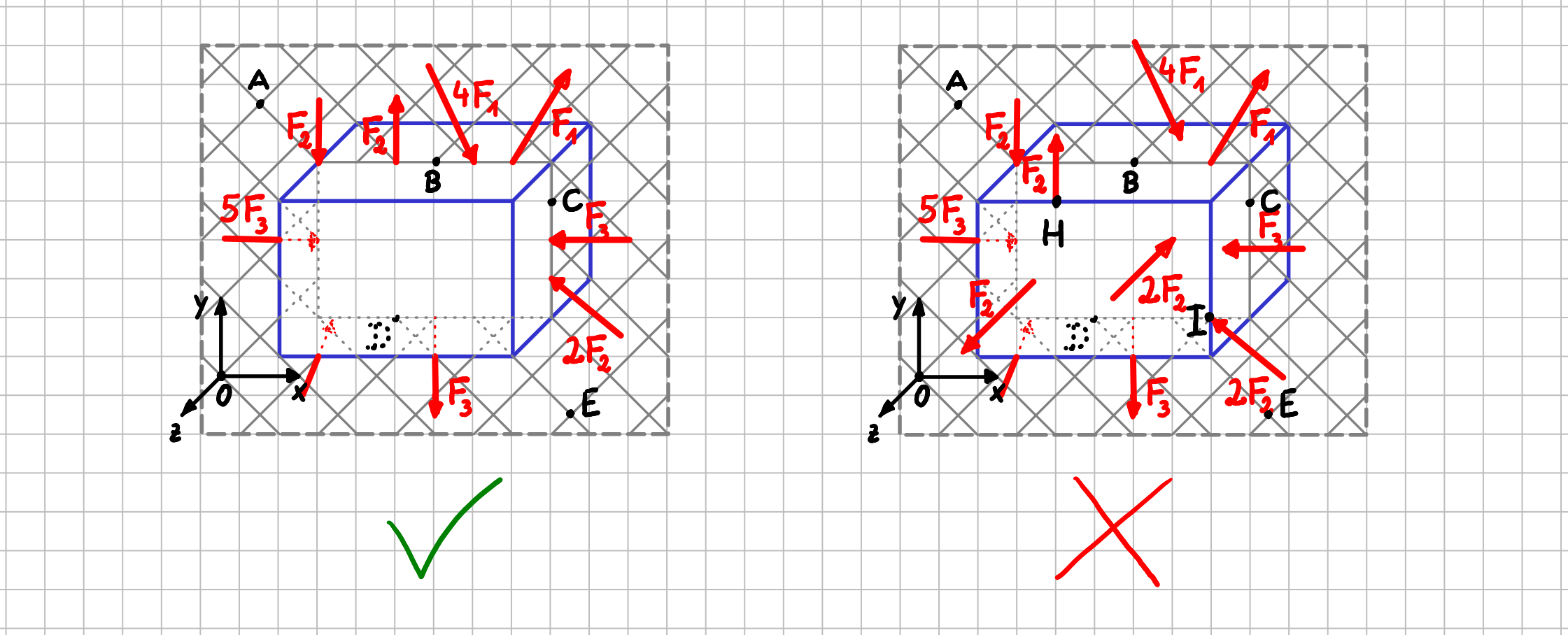
Abgrenzung ebenes Kräftesystem (links) und räumliches Kräftesystem (rechts)

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/Abgrenzung_ebenes_rauemliches_Kraeftesystem.png

Wenn du jetzt denkst, "Moment mal, es gibt doch auch noch Momente?!?", dann liegst du genau richtig. Kräfte, die in der \( xy- \)Ebene liegen, haben \( - \) je nach gewähltem Bezugspunkt \( - \) eine Momentenwirkung um die \( z- \)Achse. In einem ebenen Kräftesystem können aber auch noch freie Einzelmomente um die \( z \)-Achse auftreten. Wenn du jetzt etwas entrüstet sagst: "Aber dann gibt es ja doch etwas, was außerhalb der \( xy- \)Ebene, also in \( z -\)Richtung wirkt!", dann hast du nur im ersten Moment recht. Ein Einzelmoment um die \( z- \)Achse ist ja die Wirkung eines Kräftepaars. Und diese beiden Kräfte liegen dann wieder in der \( xy- \)Ebene.

Machen wir es konkret: Die beiden Kräfte '\( 4F_2 \)' bilden genau so ein Kräftepaar. Was waren nochmal die Bedingungen für ein Kräftepaar? 1) Der Betrag der beiden Kräfte ist gleich groß; 2) die Wirkungslinien sind parallel; 3) die Kräfte wirken in die entgegengesetzte Richtung. All das ist hier für die beiden Kräfte '\( 4F_2 \)' gegeben. Ihre Wirkung ist also einzig und allein ein Moment, das um die \( z- \)Achse wirkt; die Ursache, die beiden Kräfte selbst, liegt aber in der \( xy-\)Ebene.

Hier findest du alles aus dem bisherigen Abschnitt auch noch einmal im Video erklärt:

Schauen wir uns noch ein reales System an. Wie kannst du entscheiden, ob du ein reales System als ein ebenes oder als ein räumliches System modellieren kannst? Es hängt einzig und allein davon ab, was du untersuchen möchtest.

Wenn dich bei der dargestellten Brücke z.B. 'nur' die Belastungen der Seile oder Lager aufgrund der Belastungen durch das Eigengewicht der Brücke und dem Verkehr interessiert, reicht es aus, die Brücke als ebenes System zu modellieren: Alle genannten Kräfte liegen in der Brückenebene.

Wenn dich jedoch auch noch interessiert, welchen Einfluss Windlasten haben, die ja je nach Windrichtung aus allen möglichen Richtungen kommen können, musst du die Brücke als räumliches System modellieren: Es treten dann in jedem Fall auch noch Kraftkomponenten senkrecht zur Brückenebene auf.

Brücke mit Eigengewicht und Belastung durch Fahrzeuge

Weitere Informationen

Leonardo Pallotta
CC BY 2.0
https://www.flickr.com/photos/83265757@N00/73471268

Räumliches Kräftesystem

Nachdem jetzt klar ist, was ein ebenes Kräftesystem ist, ist die Definition eines räumlichen Kräftesystems eigentlich schon ein Selbstgänger, oder? 

Bei einem räumlichen Kräftesystem können die Wirkungslinien der Kräfte Komponenten in alle drei Koordinatenrichtungen haben. 

Ein Beispiel ist das rechte System im vorletzten Bild. Oder ein fahrendes Auto, bei dem der Wind von schräg vorne kommt: die Gewichtskraft \( F_G \) wirkt in \( y- \) Richtung. Die aus dem Wind resultierende Kraft \( F_W \) liegt in der \( xz- \)Ebene und kann in ihre Komponenten \( F_{w_x} \) und \( F_{w_z} \) in \( x-\) und \( z- \)Richtung zerlegt werden. 

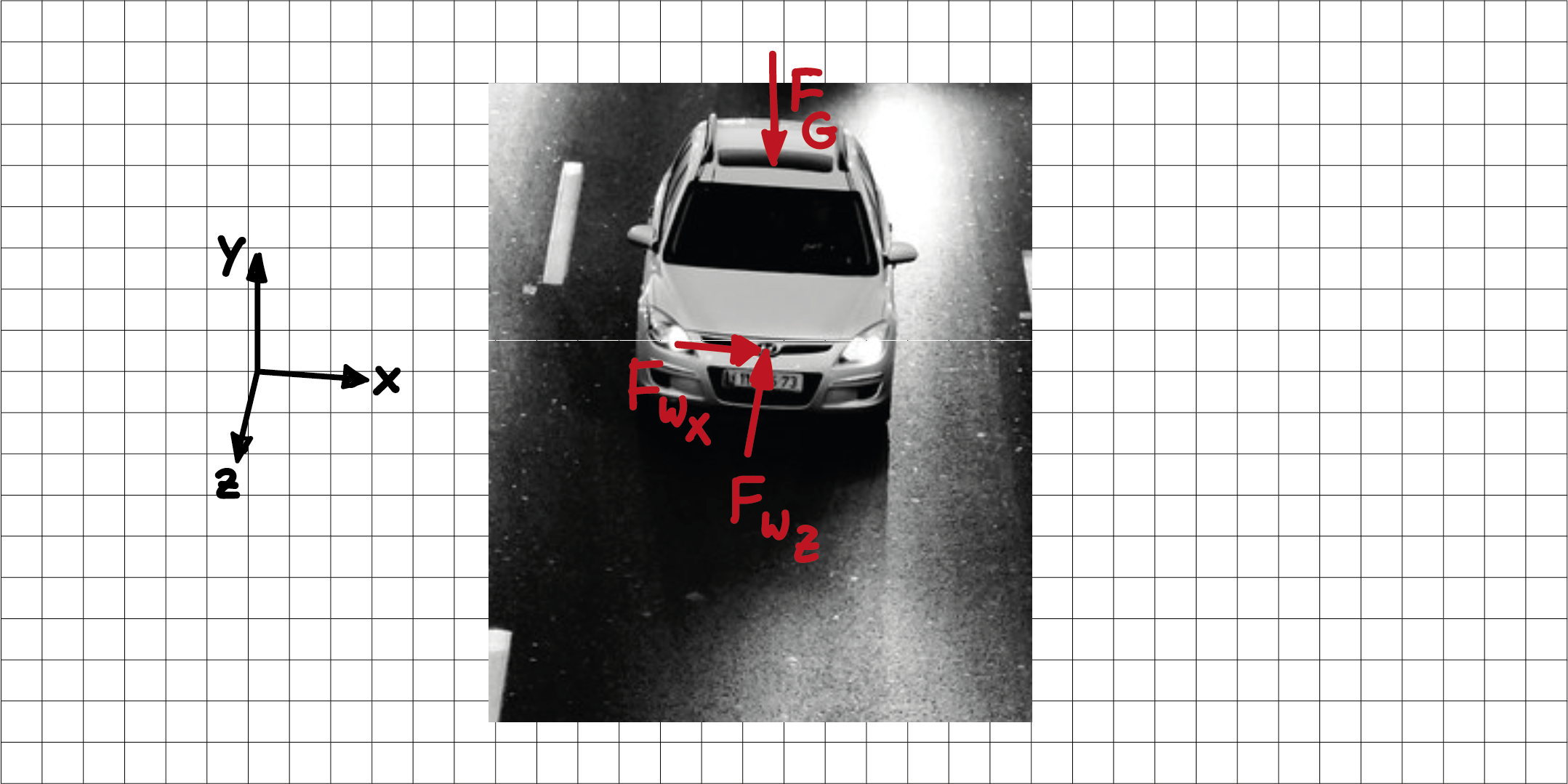
Räumliches Kräftesystem: Fahrzeug mit Belastungen durch Gewichtskraft und Wind

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg (Ausschnitt und handschriftliche Ergänzungen) auf Basis von RG in TLV
CC BY 2.0
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/Raeumliches_Kraeftesystem_Fahrzeug_mit_Windlast_und_Gewichtskraft.png
https://www.flickr.com/photos/30845197@N00/22028571392

Auch das, was wir über Momente für das ebene System festgestellt haben, lässt sich natürlich für das räumliche Kräftesystem übertragen und erweitern: Auch im räumlichen Kräftesystem treten natürlich Momentenwirkungen und Einzelmomente auf. Sie können Komponenten in alle Koordinatenrichtungen haben, da ja Kräftepaare mit Wirkungslinien in alle drei Achsrichtungen auftreten können.

Zusammenfassung - Das Wichtigste in Kürze

Kräftesysteme
Mit einem Kräftesystem sind alle auf einen Körper wirkenden Kräfte gemeint.
In einem ebenen Kräftesystem liegen die Wirkungslinien aller Kräfte in einer Ebene. Für die resultierenden Momente und die Einzelmomente bedeutet dies, dass sie ausschließlich um die Achse senkrecht zu dieser Ebene wirken.

Beispiel für ein ebenes System in der \( xy- \)Ebene:

Die Wirkunglinien aller Kräfte und ihre Ortsvektoren liegen in der \( xy- \)Ebene. Momente wirken nur um die \(z-\)Achse.

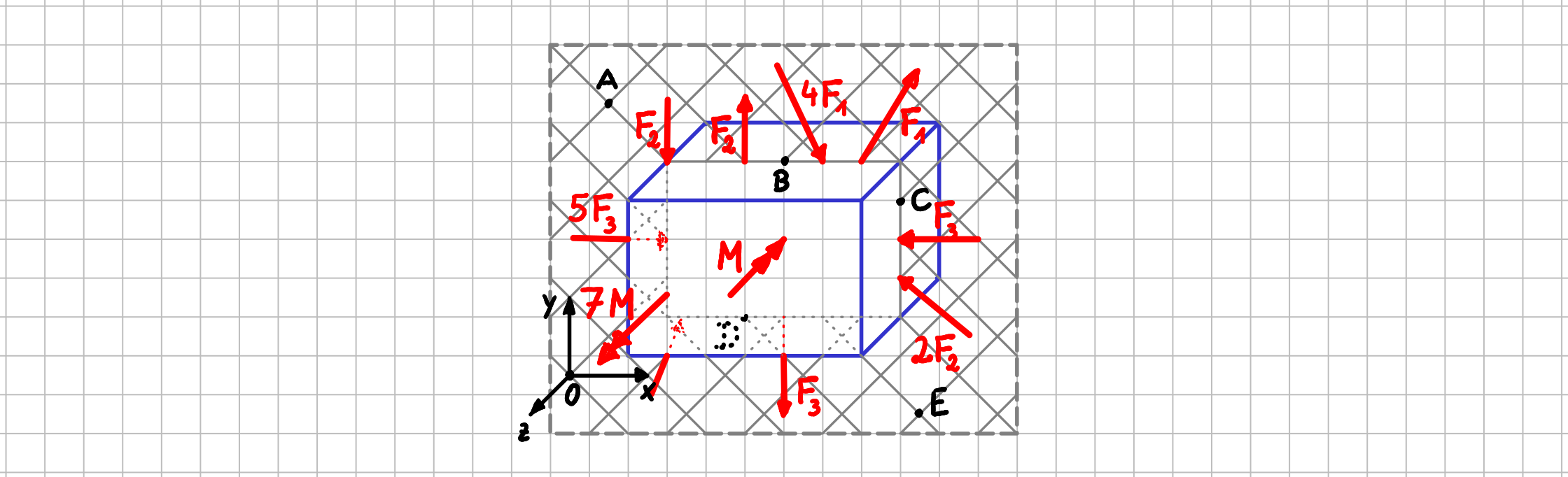
Ebenes Kräftesystem

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/Ebenes_Kraeftesystem_Zusammenfassung.png

In einem räumlichen Kräftesystem  liegen Wirkungslinien und Ortsvektoren von Kräften nicht mehr alle in einer Ebene. Oft gibt es Kräfte mit Komponenten in alle drei Raumrichtungen. Momente oder Momentenkomponenten können daher auch um alle drei Achsen wirken.

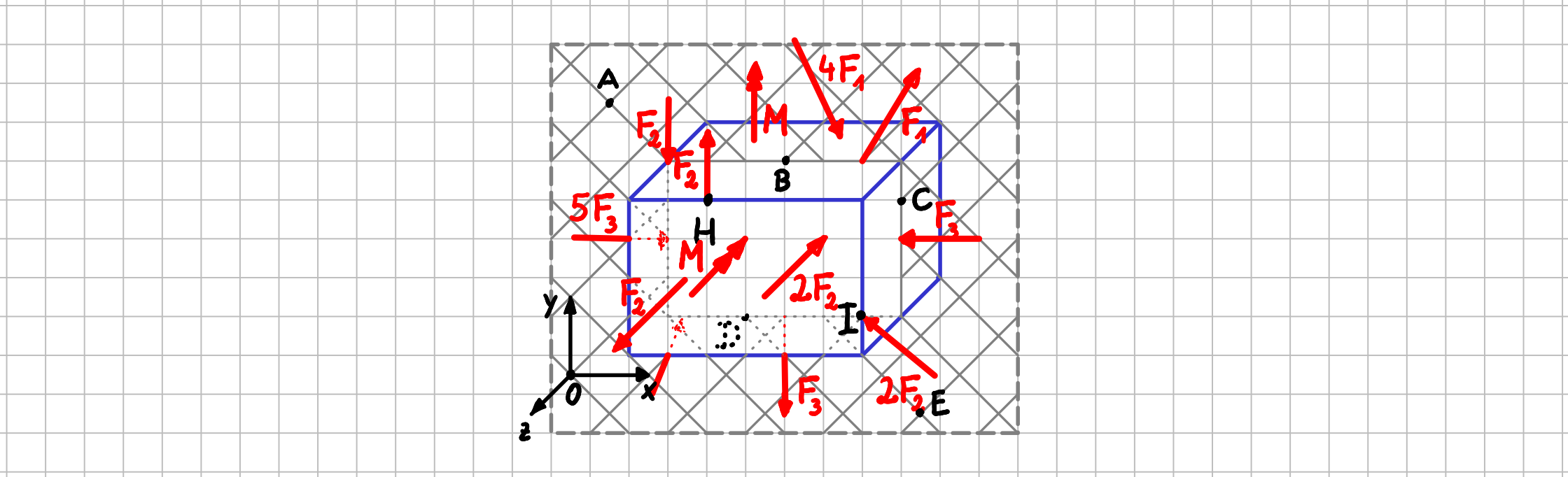
Räumliches Kräftesystem

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2164/raeumliches_Kraeftesystem_Zusammenfassung.png