Zum Hauptinhalt
Details

Kraft

Kraft

Zurück
Weiter

2. Grundlagen

2.1. Beschreibung und Darstellung

Beschreibung und Darstellung von Kräften

Kräfte sind vektorielle Größen. Sie lassen sich also als Vektor mit Betrag und Richtung darstellen. Genauer gesagt sind Kräfte gebundenen Vektoren. Aber der Reihe nach.

Stell dir vor, du bist die Person auf dem folgenden Bild. Plötzlich kommt Wind auf und die Kraft, die eine Böe auf dich ausübt, hat eine Größe von \(200\mathrm{N}\). Es macht einen erheblichen Unterschied, ob diese Kraft von links oder von rechts auf dich einwirkt, oder? Einmal geht es für dich Richtung Sicherheit, einmal Richtung Abgrund.


Kräfte sind nicht nur Vektoren, sie sind gebundene Vektoren. 
Was ist das denn nun schon wieder? Und gibt es dann auch ungebundene/freie Vektoren? Ja, die gibt es. Aber da Kräfte nun mal gebundene Vektoren sind, konzentrieren wir uns erst einmal darauf.

Mit der Gewichtskraft lässt sich sehr einfach veranschaulichen, was es bedeutet, dass die Kraft ein gebundener Vektor ist.

Stell dir ein Pendel vor. Das kann z.B. ein Stein an einem Faden oder ein Lot auf einer Baustelle sein.  Wenn du dieses Pendel auslenkst, dann schwingt es hin und her. 

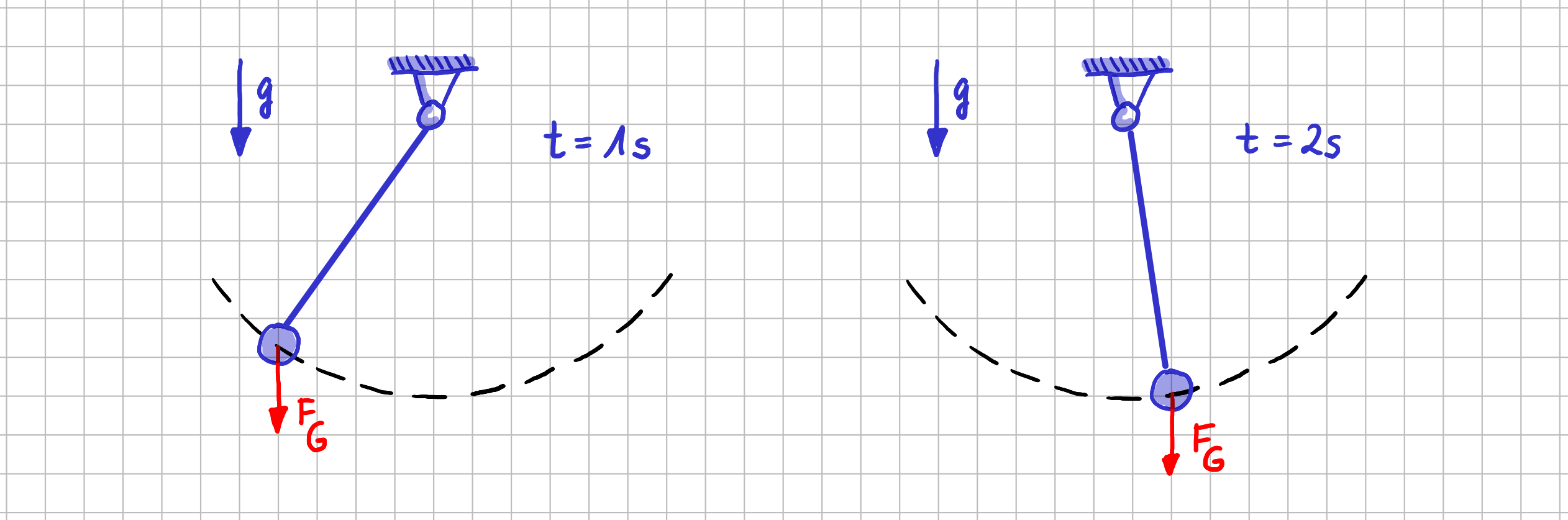
Kraft als gebundener Vektor am Beispiel der Gewichtskraft

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2163/Kraft_als_gebundener_Vektor_am_Beispiel_Gewichtskraft.png


Das Pendelobjekt (Stein oder Senkblei) hat aufgrund seiner Masse \( - \)nehmen wir an es seien \( 500\mathrm{g} \) \( - \) eine Gewichtskraft  von \( 0,5\mathrm{kg} \cdot 9,81 \frac{\mathrm{kg}}{\mathrm{m} \cdot \mathrm{s}^2} \approx 5\mathrm{N} \). Und der Angriffspunkt dieser Masse "bewegt sich mit dem Objekt mit". Um die Gewichtskraft korrekt beschreiben zu können, braucht es also zusätzlich zu Betrag \( 5\mathrm{N} \) und Richtung (in Richtung des Erdmittelpunktes, also in Richtung des Vektors der Erdbeschleunigung \( \vec{g} \) ) auch noch den Angriffspunkt des Vektors. Und dieser Angriffspunkt ist der Schwerpunkt des Pendelobjektes.

Für einen gebundenen Vektor sind also drei Informationen erforderlich: 

  1. Betrag, 
  2. Richtung und 
  3. Lage des Angriffspunktes.


Wenn du einmal am eigenen Körper spüren willst, genauer gesagt in deinem Schultergelenk, dass die Kraft ein gebundener Vektor ist, ihre Wirkung also von der Lage des Angriffspunktes abhängt, dann mach doch einfach mal den folgenden Versuch.
Streck beide Arme seitlich aus. Jetzt bittest du jemand, mit der gleichen Kraft beim rechten Arm auf dein Handgelenk nach unten zu drücken, und linken Arm auf dein Schultergelenk. Dein Aufgabe ist es, beide Arme in der horizontalen Position zu halten.
Die beiden Kräfte sind dann gleich, was den Betrag und die Richtung angeht. Nur ihr Angriffspunkt relativ zum Schultergelenk ist unterschiedlich.

Die Lage des Angriffspunktes hat auf die Wirkung einer Kraft einen großen Einfluss.

Weitere Informationen

yanalya, Zuschnitt und Eintragungen Johanna Peters
Freepik-Lizenz
https://de.freepik.com/fotos-kostenlos/glueckliches-maedchen-zeigt-zwei-uebungen-fuer-arme_937106.htm


Na, merkst du die unterschiedliche Wirkung der beiden Kräfte?
Wenn du dich auf deine Schultergelenke konzentriertst, merkst du sie daran, dass du auf der rechten Seite über die Muskeln rund um das Schultergelenk ein Moment aufbringen musst, um die Abwärtsbewegung (Drehung) des Arms zu verhinden und den Arm in der horizontalen Lage zu halten. Auf der linken Seite ist das nicht nötig.


Wenn du die Informationen für einen gebundenen Vektor wie z.B. die Kraft angeben willst, reicht es also nicht aus, den Betrag und den Kraftvektor an sich aufzuschreiben. Du musst zusätzlich noch die Lage des Angriffspunktes kennen.
Für einen allgemeinen Kraftvektor sieht das dann so aus, wenn wir der Einfachheit der Darstellung halber mal annehmen, dass der Kraftvektor in der \(xy-\)Ebene wirkt.

Darstellung eines allgemeinen Kraftvektors (gebundener Vektor) mit Angabe von Betrag, Richtung und Lage des Angriffspunktes

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2163/Darstellung_eines_allgemeinen_Kraftvektors_als_gebundener_Vektor.png


Im Kapitel "Moment" kannst du dich ausführlich auch mit der Momentenwirkung von Kräften beschäftigen. Momente sind auch vektorielle Größen. Allerdings sind sie im Gegensatz zu Kräften ungebunde Vektoren.

Zusammenfassung - Das Wichtigste in Kürze

Kräfte sind ortsgebundene Vektoren. 

Für ihre Beschreibung sind daher drei Angaben erforderlich

  1. der Betrag
  2. die Richtung
  3. der Angriffspunkt
Für die Gewichtskraft eines nahezu vollbeladenen Containers mit homogener Verteilung des Inhalts können die drei Angaben so gegeben werden:

Gewichtskraft eines Containers als Beispiel für einen gebundenen Vektor

Weitere Informationen

Kevin Hackert, handschriftliche Ergänzungen von Johanna Peters TUHH
CC BY-NC 2.0
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2163/Gewichtskraft_eines_Containers.png



Zurück
Weiter