Kraft
Kraft
2. Grundlagen
2.4. Zulässige Operationen
Zulässige Operationen bei Kräften
Es gibt gewisse Operationen, die du mit Kräften durchführen kannst, ohne dass sich die "Wirkung nach außen" ändert.
Bevor wir uns überlegen können, was überhaupt Operationen sind, die man mit Kräften durchführen kann, müssen wir uns erstmal anschauen, was mit "Wirkung nach außen" gemeint ist. Nur dann können wir verstehen, warum gewisse Operationen erlaubt sind und andere nicht.
Mit "Wirkung nach außen" ist gemeint, dass sich -obwohl man eine Operation mit einer Kraft ausführt- am Gesamtverhalten des Systems nichts ändert: Die Lagerreaktionen bleiben also gleich.
Wenn du ganz neu im Bereich Mechanik unterwegs bist, solltest du an dieser Stelle erst die Kapitel "Freischneiden & Actio=Reactio" sowie "Gleichgewichtsbedingungen" durcharbeiten, damit du alles im Folgenden verstehen kannst.
Oder du machst auch ohne Kenntnis dieser beiden Kapitel hier erst einmal weiter und kommst nachdem du die beiden Kapitel erarbeitet hast, ein zweites Mal hierher zurück.
Wenn du dich schon mal mi Gleichgewichtsbedingungen beschäftigt hast, sollten dir die folgenden Darstellungen hoffentlich schnell einleuchten.
Machen wir es konkret: Was kannst du mit der Kraft in den beiden folgenden Systemen 'anstellen', ohne dass sich die Lagerreaktionen (Beträge und Richtungen) verändern?

Ausgangssysteme mit Kräften
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Ausgangssysteme_mit_Kraeften.png
Wenn das Kriterium für erlaubte Kräfteoperationen ist, dass sich die Lagerreaktionen nicht ändern dürfen, müssen die Lagerreaktionen erstmal durch Freischneiden sichtbar gemacht werden. Das Ergebnis für die beiden Systeme sieht so aus:
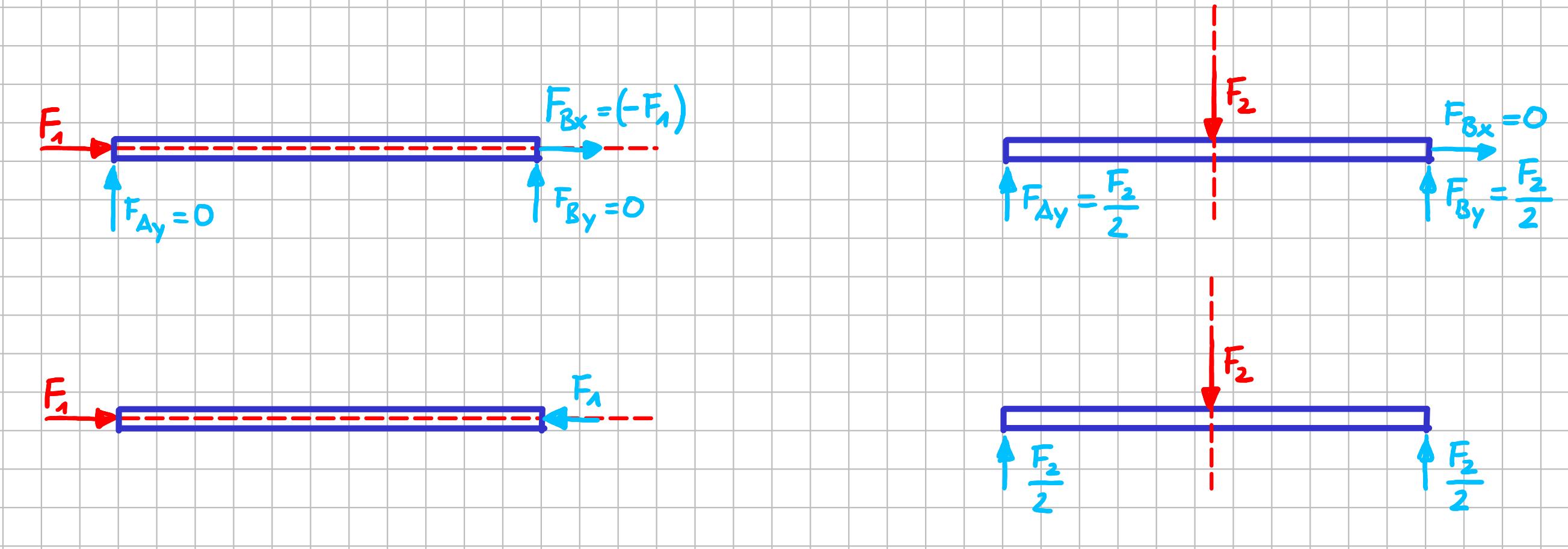
Freikörperbilder der Ausgangssysteme
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Freikoerperbilder_der_Ausgangssysteme.png
Damit leichter zu überblicken ist, welche Kräfte die ursprüngliche Belastung und welche die Lagerreaktionen sind, wurden die Lagerreaktionen ausnahmsweise in hellblau dargestellt.
Wenn die äußeren Kräfte \( F_1 \) und \( F_2 \) entlang ihrer Wirkungslinie verschoben werden, ändert das nichts an den Lagerreaktionen.

Kräfte verschoben entlang ihrer Wirkungslinien
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Kraefte_verschoeben_entlang_ihrer_Wirkungslinie.png
Verschieben einer Kraft entlang ihrer Wirkungslinie ist also eine zulässige Operation, da sich die Wirkung nach außen dadurch nicht ändert.
Und was ist mit dem Verschieben parallel zur Wirkungslinie? Das ist ja die logische nächste Frage. Schauen wir uns das anhand des rechten Systems einmal an. Wenn du beim rechten System die Kraft \( F_2 \) z.B. nach rechts verschieben würdest, dann sähe das so aus:

Kraft parallel verschoben zu ihrer Wirkungslinie
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Kraefte_parallel_verschoben_zu_ihrer_Wirkungslinie.png

Nullvektoren addieren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Nullvektoren_addieren.png
Für die praktische Anwendung ist diese Operation sicherlich nicht so relevant. Für die Betrachtungen im Zusammenhang mit der Momentwirkung von Kräften ist sie allerdings essentiell. Das wirst du im Kapitel Moment merken.
Bei der Betrachtung von mechanischen Systemen werden diese zwei zulässigen Operationen ständig verwendet: Das Addieren und Zerlegen von Kräften mit gemeinsamem Angriffspunkt.
Schauen wir uns zunächst das Addieren genauer an. Die folgenden drei Aussagen für die Kräfte \( \vec{F}_1 \), \( \vec{F}_2 \), die einen gemeinsamen Angriffspunkt haben, und ihre resultierende Kraft \( \vec{F}_{res} \) sind identisch:
- Die Kräfte \( \vec{F}_1 \) und \( \vec{F}_2 \) greifen an einem Punkt an. Ihre Wirkung ist identisch der Wirkung der resultierenden Kraft \( \vec{F}_{res} \), wenn \( \vec{F}_{res} \) aus der Parallelogramm-Konstruktion bestimmt wird.
- \( \vec{F}_1 + \vec{F}_2 = \vec{F}_{res} \)
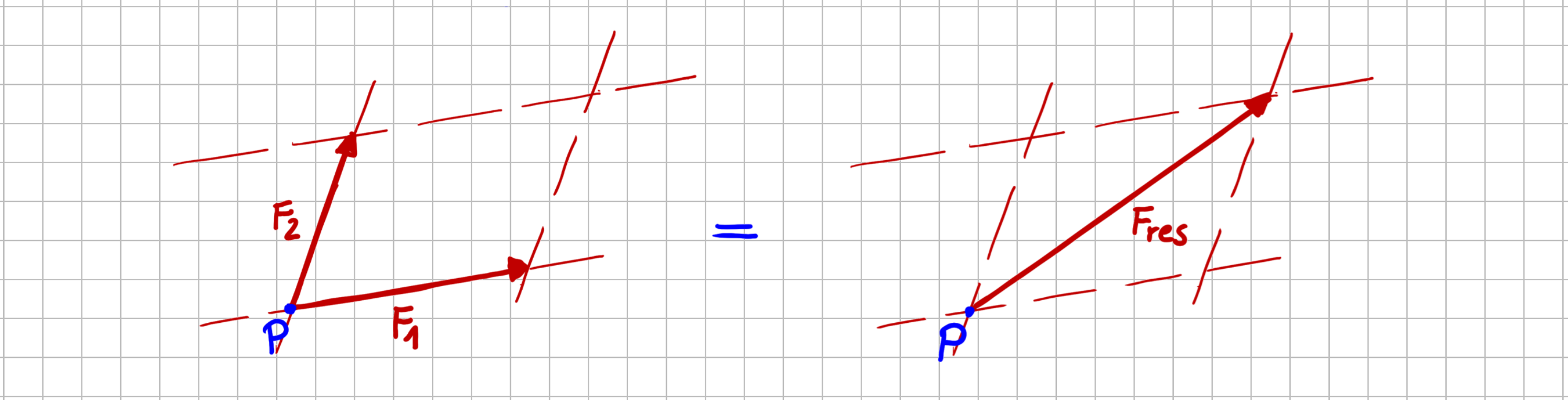
Addition von Kraftvektoren mit gemeinsamem Angriffspunkt: Konstruktion der resultierenden Kraft mittels Parallelogramm-Regel
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Addition_von_Kraftvektoren_mit_gemeinsamem_Angriffspunkt.png
Die Umkehrung gilt natürlich auch: eine Kraft kann in zwei Kräfte mit demselben Angriffspunkt zerlegt werden, wenn die Parallelogramm-Regel verwendet wird. Diese Form der Kraftzerlegung kennst du vielleicht schon aus einer ganz praktischen Anwendung: Wenn sich ein Fahrzeug festgefahren hat, kannst du es mit einem weiteren Fahrzeug, das die Kraft \( \vec{F} \) aufbringt, freischleppen. Oder du verwendest zwei Fahrzeuge oder auch Seilwinden, die die Kräfte \( \vec{F}_1 \) und \( \vec{F}_2 \) aufbringen und zwar so, das die resultierende Kraft \( \vec{F}_{res} \) wieder genau \( \vec{F} \) ist.
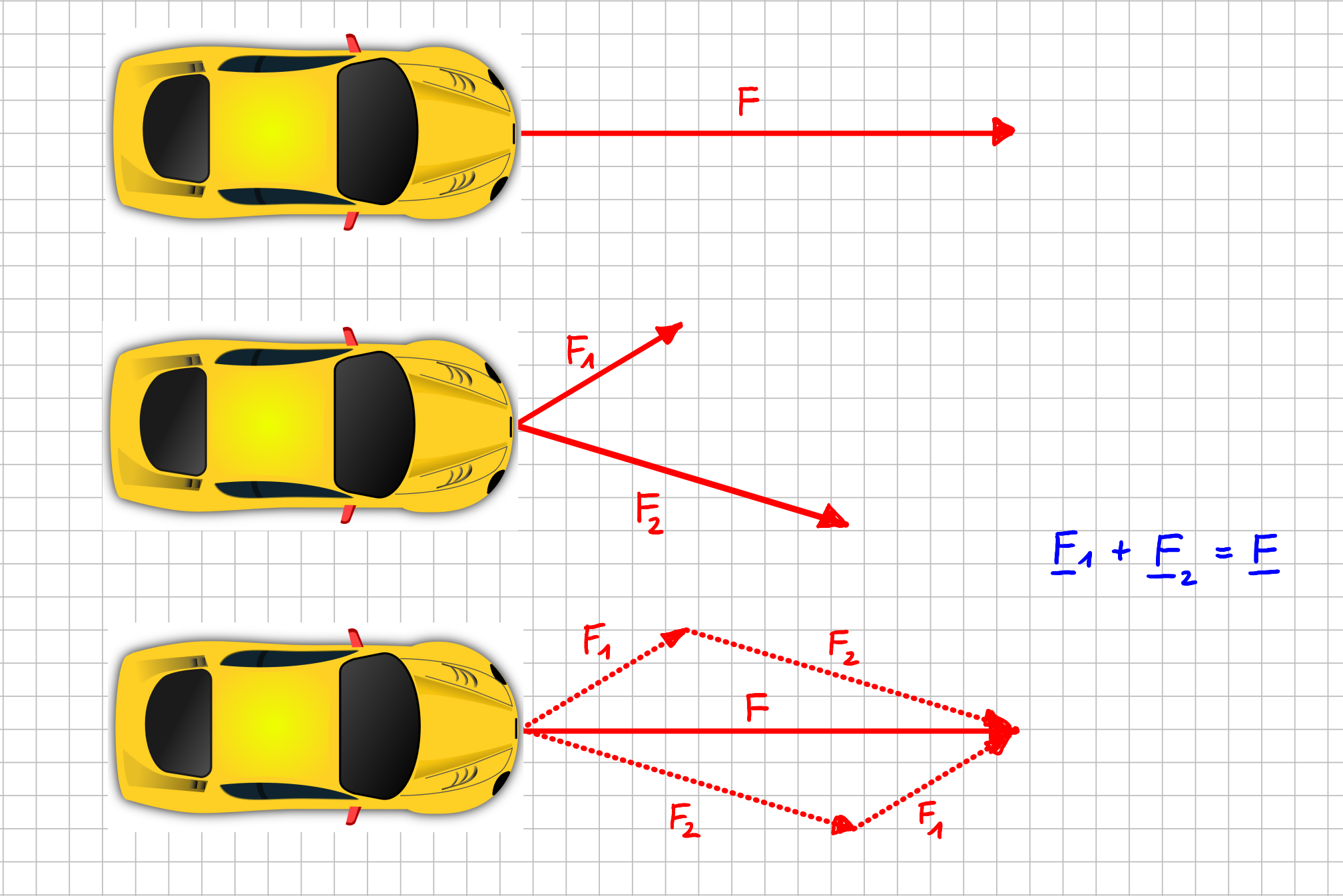
Anwenden der Kraftzerlegung beim Freischleppen eines Fahrzeugs
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg, auf der Basis von von Peeyush.ciit
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Anwenden_der_Kraftzerlegung_beim_Freischleppen_eines_Fahrzeugs.png https://upload.wikimedia.org/wikipedia/commons/c/cf/Travel-car-topview.svg
Bei der Betrachtung von mechanischen Systemen verwenden wir diese Zerlegung wirklich sehr oft. Meist werden Kräfte in ihre Komponenten bezüglich eines gegebenen Koordinatensystem zerlegt. Und da die Achsen dieses Koordinatensystems senkrecht zueinander stehen, sieht die Zerlegung dann so aus:
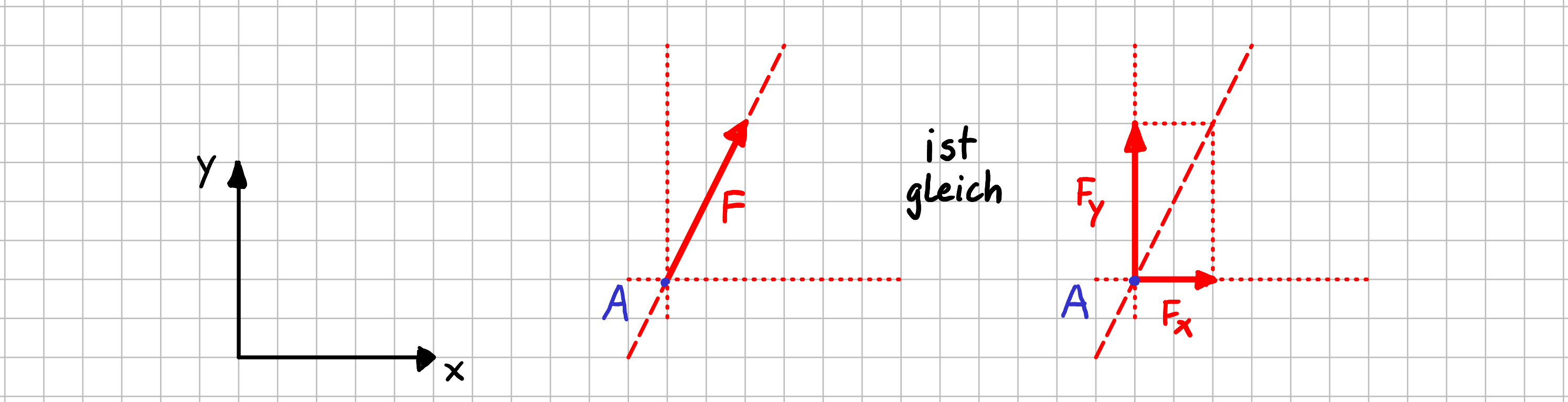
Zerlegung eines Vektors in seine Komponenten im karthesischen Koordinatensystem
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13817/mod_book/chapter/2161/Zerlegung_eines_Vektors_in_seine_Komponenten.png
Zusammenfassung - Das Wichtigste in Kürze
Operationen mit Kräften, die die Wirkung nach außen nicht verändern
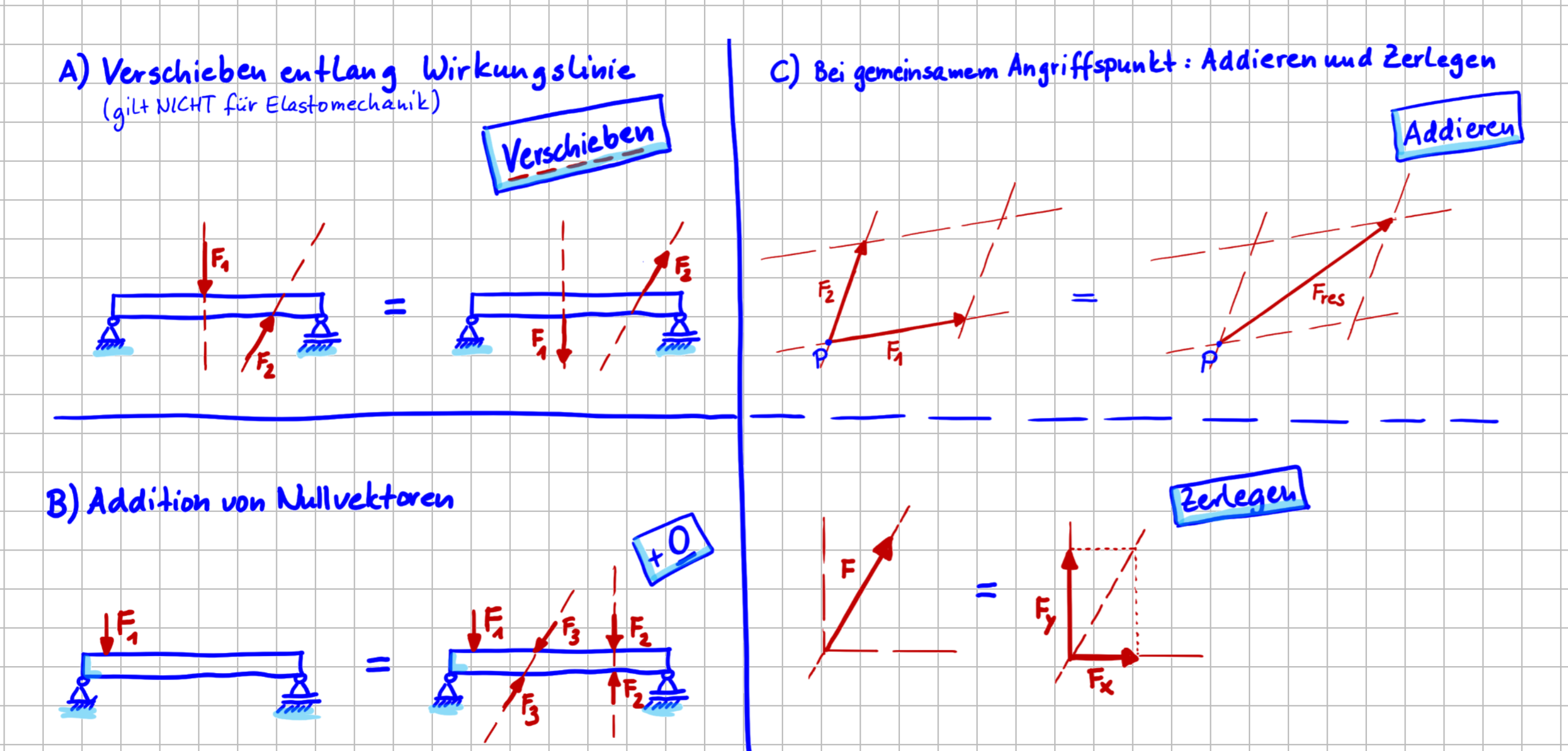
Zusammenstellung von Operationen mit Kräften ohne Veränderung der Wirkung nach außen
Weitere Informationen
Damit solltest du nun die wichtigsten Operationen, die mit Kräften erlaubt sind, kennen.