Vektorrechnung: Subtraktion

3. Rechenoperationen

3.3. Subtraktion

Subtraktion von Vektoren

Die Subtraktion zweier Vektoren $ \vec{d} $ und $ \vec{e} $ wird analog zur Addition ausgeführt und liefert ebenfalls einen Vektor als Ergebnis. Dies sei $ \vec{f} $ $$ \vec{d}=\begin{pmatrix} d_1 \\ d_2 \\ d_3 \end{pmatrix} \qquad \vec{e}=\begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix} \quad \rightarrow \quad {\vec{d}-\vec{e}=\begin{pmatrix} d_1-e_1 \\ d_2-e_2 \\ d_3-e_3 \end{pmatrix} =\vec{f}} $$

Zahlenbeispiel

$$ \vec{d}=\begin{pmatrix} 7 \\ 2 \\ -4 \end{pmatrix} \qquad \vec{e}=\begin{pmatrix} -3 \\ 2 \\ 8 \end{pmatrix} \quad \rightarrow \quad\vec{d}-\vec{e}=\begin{pmatrix} 7-(-3) \\ 2-2 \\ -4-6 \end{pmatrix} =\begin{pmatrix} 10 \\ 0 \\ -12 \end{pmatrix} $$

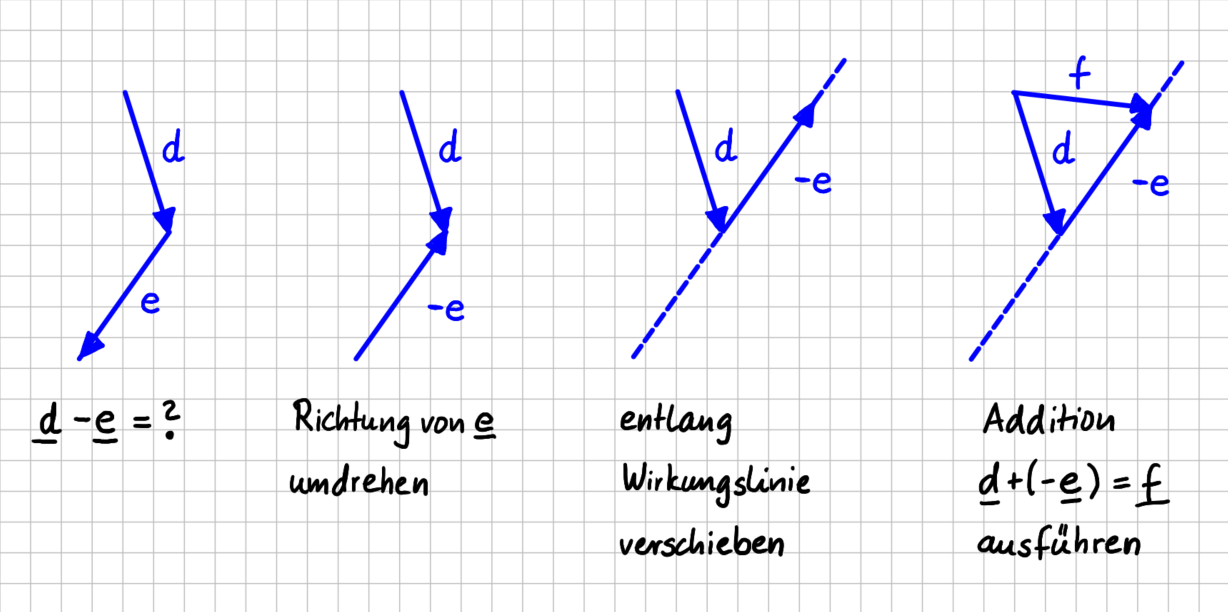
Was bei der Subtraktion passiert, lässt sich mit den bisherigen Kenntnissen sehr leicht veranschaulichen. Die Subtraktion lässt sich als Addition umschreiben: $$\vec{d}-\vec{e} = \vec{d}+(-1)\cdot\vec{e}$$ Und da bereits bekannt ist, dass die Multiplikation eines Vektors mit $(-1)$ lediglich die Richtung des Vektors umgekehrt, kann das identische Vorgehen wie bei der Addition angewendet werden, wie es in der folgenden Abbildung veranschaulicht ist.

Subtraktion von Vektoren

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2148/Subtraktion_von_Vektoren.png

Zusammenfassung - Das Wichtigste in Kürze

Subtraktion von Vektoren

Wenn zwei Vektoren $\vec{d}$ und $\vec{e}$ von einander abgezogen werden, ist das Ergebnis wieder ein Vektor. Dies sei $\vec{f}$ . Die Komponenten von $\vec{f}$ ergeben sich, indem die Komponenten von $\vec{d}$ und $\vec{e}$ einzeln voneinander abgezogen werden.

$$\vec{d}=\begin{pmatrix} d_1 \\ d_2 \\ d_3 \end{pmatrix} \qquad\vec{e}=\begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix} \quad \rightarrow \quad {\vec{d}-\vec{e}=\begin{pmatrix} d_1-e_1 \\ d_2-e_2 \\ d_3-e_3 \end{pmatrix} =\vec{f}}$$

Bei der Subtraktion von Vektoren ist die Reihenfolge nicht vertauschbar, d.h. das Kommutativgesetz gilt nicht:

$$\vec{d} - \vec{e} \neq \vec{e} - \vec{d}$$

Graphisch lässt sich die Subtraktion ebenfalls als "Hintereinanderschaltung" der beiden Vektoren verstehen, wenn in einem Vorabschritt die Richtung des abzuziehenden Vektors umgedreht wird:

Subtraktion von Vektoren

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2148/Subtraktion_von_Vektoren.png

Test - Jetzt bist du dran

Du kannst den Test nur durchführen, wenn du in "Mechanik hautnah" als Teilnehmer/in eingeschrieben bist. Wie das geht, ist hier erklärt.

Subtrahiere verschiedene Vektoren