Vektorrechnung
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Vektorrechnung |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 18:11 |
1. Einleitung Vektorrechnung
Einleitung Vektorrechnung
In der Lektion Vektorrechnung geht es um Vektoren und darum, wie du mit ihnen rechnen kannst.
Wenn du bisher also den Vektor vor lauter Pfeilen nicht gesehen hast, dann wird sich das mit dieser Lektion sicherlich ändern.
Überall Pfeile?
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2141/ueberall_Pfeile.png
Jeder Mensch hat ein Gespür dafür, was ein Vektor ist, selbst wenn er den Begriff noch nie gehört hat.
"Was für ein Quatsch ist das denn?", denkst du jetzt? Warte. Ich beweise es dir.
Du weißt doch auch, wie es sich anfühlt, wenn man in einem Auto sitzt und um eine enge Kurve fährt, stimmt's? Oder dass es einen Unterschied macht, ob du beim Ballsport den Ball von vorne oder von der Seite an den Kopf geworfen bekommst; oder dass man manchmal "das andere links" meint, richtig?
Also hast du in jedem Fall schon ein Gespür dafür, was Vektoren sind.
In dieser Lektion hast du die Möglichkeit, dich dem Thema Schritt für Schritt zu nähern. Du erarbeitest dir, was ein Vektor ist und wie er dargestellt wird - mathematisch und graphisch. Anschließend lernst du die grundlegenden Rechenmethoden für Vektoren kennen. Plus-, Minus- Mal- und Geteiltrechnen mit Zahlen kannst du bestimmt ganz gut. Du wirst sehen, auch für Vektoren gibt es verschiedene Rechenarten. Und die sind eigentlich auch ganz einfach zu lernen.
Für alle Rechenmethoden findest du unterschiedliches Trainingsmaterial.
Test - Vektorrechnung Mischmasch
2. Was ist ein Vektor eigentlich?
Was ist ein Vektor eigentlich?
Wenn du das Wort “Vektor” hörst, reagierst du automatisch in irgendeiner Form. Du kannst gar nicht anders. Diese Reaktion wird von Mensch zu Mensch unterschiedlich sein, aber tendenziell eher positiv – Cool, Vektoren! – oder eher negativ – Oje, schon wieder Vektoren! – gefärbt sein.
Egal, wie deine ganz individuelle Reaktion ausfällt, erlaub dir gerade in dem Fall, in dem du tendenziell negativ reagierst, das Thema “Vektoren” noch einmal ganz neu kennenzulernen. Du wirst in diesem Abschnitt sehen, warum es sich lohnt.
Stell dir vor, du bist irgendwo in einer Stadt, in der du dich nicht so gut auskennst. Du bist auf der Suche nach einem Bäcker und fragst jemanden auf der Straße nach dem Weg: “Wo ist denn hier der nächste Bäcker?”. Wenn du als Antwort bekommst, “Der ist etwa 500m von hier.” weißt du schon mal, dass du nur etwa 5 Minuten brauchen wirst, um dorthin zu kommen. Du hast aber noch keine Idee, in welche Richtung du gehen musst. Die reine Angabe der Streckenlänge hilft dir also nur bedingt weiter. Du kommst erst zum Ziel, wenn du auch noch Informationen über die Richtung bekommst, in die du gehen musst. Vermutlich wird die Person, die du gefragt hast, dir mit einer Hand noch die Richtung zeigen. Damit bekommst du dann also auch noch die benötigte Richtungsinformation. Und ohne, dass du es gemerkt hast, hast du auch schon mit Vektoren zu tun. Vektoren kombinieren nämlich genau zwei Angaben: die Information über eine Länge (oder allgemeiner gesagt über einen Betrag) und die Information über die Richtung. Und wie du gerade gemerkt hast, ist es für eine Kommunikation in oder über die reale Welt ungeheuer wichtig, beide Informationen zu haben und das am besten noch zur selben Zeit.
Du wirst sicherlich zustimmen, dass es total hilfreich ist, wenn Menschen ihre Hände oder Arme verwenden, um die Richtungen eines Weges zu zeigen. In der Mathematik wird hierfür ein Pfeil verwendet. So wird es ja zum Beispiel auch im Straßenverkehr gemacht. Der Pfeil gibt die Richtung an. Und der Zahlenwert, der daneben geschrieben wird, ist die Länge, die in die angegebene Richtung zurückgelegt werden muss. Beide Informationen zusammen bezeichnet man als Vektor. Im Beispiel sähe die Situation also so aus:
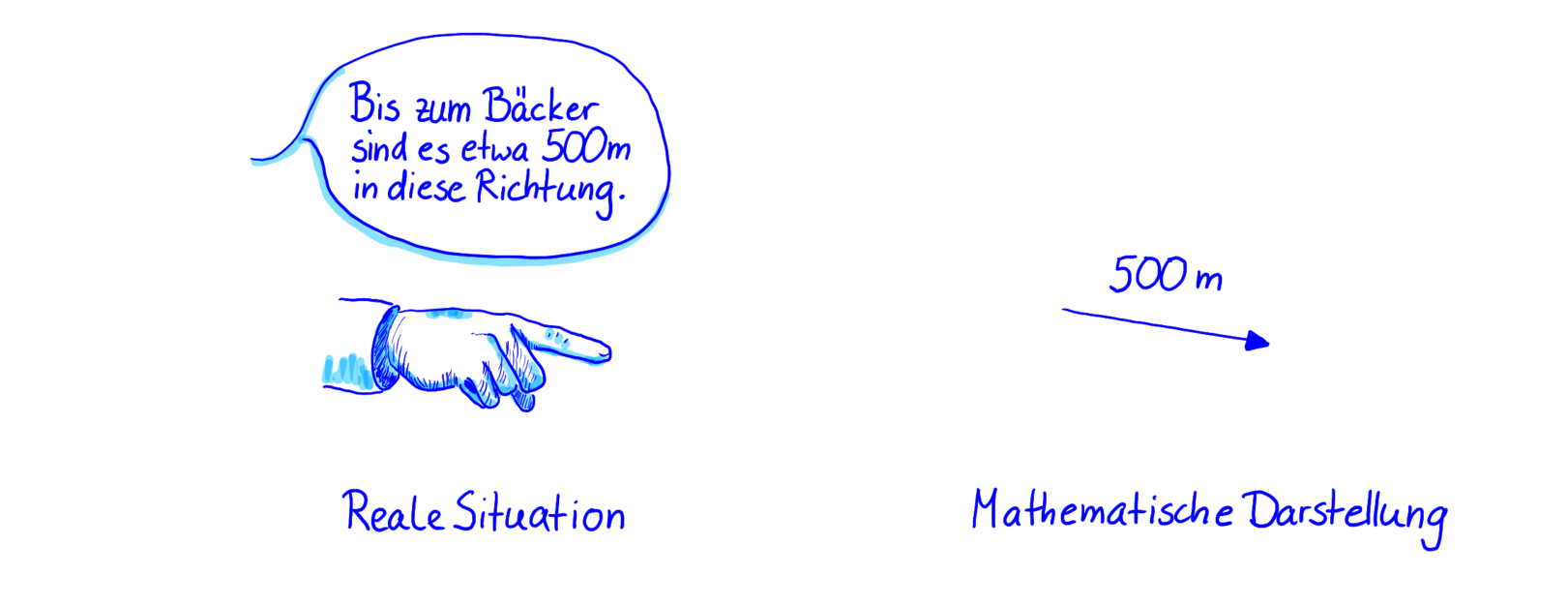
Angabe einer Weginformation mit Richtung und Betrag
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2142/Angabe_einer_Weginformation.png
Im realen Leben, und damit in der Physik, die versucht, Vorgänge im realen Leben zu beschreiben, gibt es ganz viele Größen, die die Angabe eines Betrags und einer Richtung brauchen. Sonst wären sie schlicht und einfach sinnlos und es würde zum Teil richtig gefährlich. Du findest also überall Vektoren. Wenn du auf dem Fahrrad unterwegs bist und einem Kind, das hinter einem Auto hervorspringt, ausweichen willst, dann beschleunigst oder verzögerst du in eine bestimmte Richtung. Tada, ein Vektor. Wenn du auf Skiern oder einem Mountainbike einen Hang runterfährst und in eine Linkskurve gehst, dann wirken da hoffentlich Kräfte in der richtigen Größe und in der richtigen Richtung; sonst liegst du nämlich schnell auf der Nase. Tada, schon wieder ein Vektor. Und du möchtest doch auch, dass die Ingenieurinnen und Ingenieure, die das Haus berechnet haben, in dem du wohnst, alle auftretenden Kräfte (z.B. Eigengewicht, Windlast, Schneelast) ordnungsgemäß nach Größe und Richtung berücksichtigt haben, oder? Tada, schon wieder Vektoren. Und auch die Möbel, die du nutzt, die Brücken, die du passierst, die Maschinen und Verkehrsmittel, die du nutzt, – Toaster, Föhn, Rasenmäher,Fahrrad, Roller, Bus, Auto, Flugzeug – sind hoffentlich alle so ausgelegt, dass sie allen auftretenden Belastungen – egal ob statisch oder dynamisch – standhalten. Du siehst also: Kräfte und Momente, Beschleunigungen und Geschwindigkeiten sind ganz wesentliche Vektoren und begegnen dir Tag aus Tag ein.
Es lohnt sich also wirklich, sich mit dem Konzept “Vektoren” zu beschäftigen, ja mehr noch: anzufreunden. Vektoren sind einfach unglaublich nützlich … und einfach anzuwenden, wenn man das Prinzip verstanden hat. Und genau beim (weiteren) Verstehen soll dir dieses Kapitel helfen.
In den weiteren Abschnitten findest du allgemeine Informationen zur Definition und Darstellung eines Vektors. Mit den drei Kenngrößen eines Vektors, seinem Betrag, seiner Richtung und seinem Angriffspunkt kannst du dich dann noch genauer beschäftigen.
2.1. Definition und Darstellung
Definition und Darstellung eines Vektors
Im realen Leben gibt es viele Größen – z.B. Geschwindigkeit, Beschleunigung, Kraft, Moment, Impuls, Drall – die nur vollständig charakterisiert werden können, wenn man den Betrag und die Richtung, in die die jeweilige Größe wirkt, kennt. Man nennt diese Größen daher auch gerichtete Größen. Und um genau solche Größen mathematisch beschreiben zu können, werden Vektoren verwendet. Vektoren haben eine Länge, allgemeiner sagt man auch einen Betrag, und sie geben die Richtung der Größe an, die sie beschreiben. Und es spielt eine Rolle, wo die entsprechende Größe wirkt. Informationen über die Lage oder den Angriffspunkt der Größe braucht es also auch noch.
Für die graphische Darstellung eines Vektors wird ein Pfeil verwendet. Das ist im Straßenverkehr nicht anders. Der Pfeil gibt die Richtung an.

Pfeil zur Angabe der Richtung im Straßenverkehr
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Pfeil_zur_Angabe_der_Richtung_im_Stra%C3%9Fenverkehr.png?time
In der Mathematik steht neben dem Pfeil der Betrag/die Länge des Vektors. Das kann eine Zahl oder eine Variable sein. Im Fall einer Kiste mit einer Masse von \(m_1=10\mathrm{kg}\) , also einer Gewichtskraft von etwa \( G_1 = m_1 \cdot g= 100\mathrm{N} \) , sieht das dann so aus. Eine doppelt so schwere Kiste ist in der Abbildung ebenfalls dargestellt.
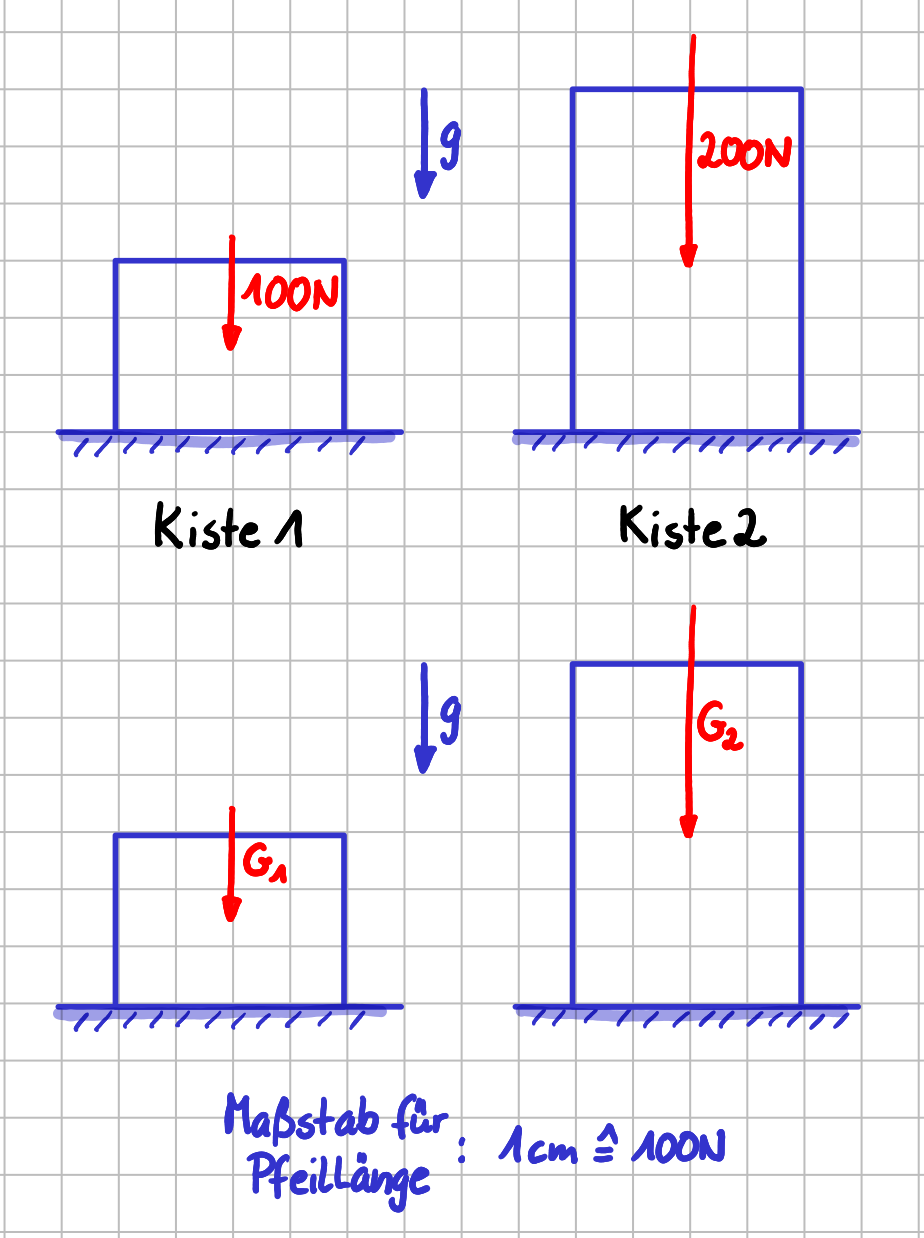
Verschiedene Darstellungsvarianten für den Betrag eines Vektors: maßstäbliche Pfeillänge
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Verschiedene_Darstellungsvarianten_Vektor_01.png
Werden Vektoren maßstäblich gezeichnet, entspricht die Länge des Pfeils dem Betrag des Vektors. Ein doppelt so langer Pfeil bedeutet dann also, dass die Gewichtskraft des zweiten Objektes doppelt so groß ist. In dieser Darstellungsvariante enthält der Pfeil also die Richtungs – und die Betragsinformation, so lange der Maßstab bekannt ist. Die Angabe des Betrags als "Zahl daneben" ist dann theoretisch doppeltgemoppelt, dient aber in jedem Fall der Übersicht.
Oft werden aber alle Pfeile gleich lang dargestellt.
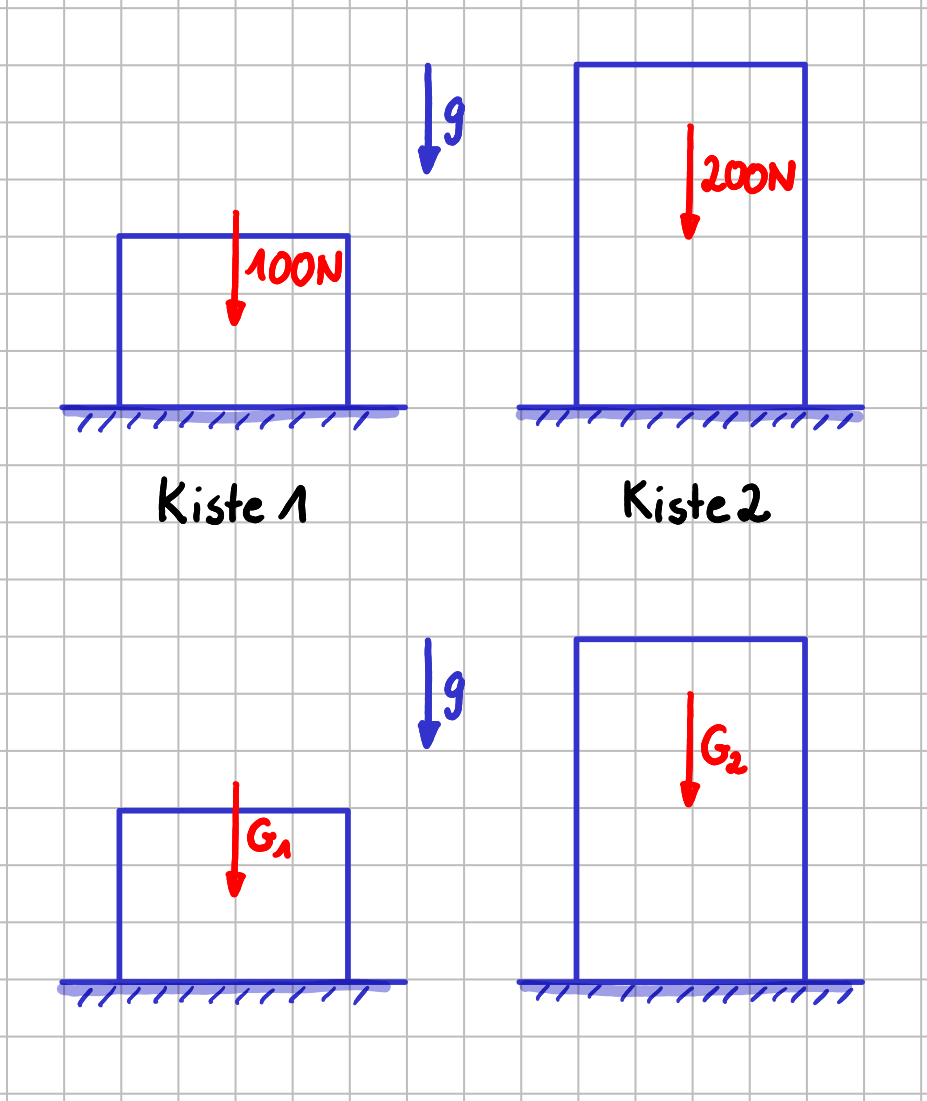
Verschiedene Darstellungsvarianten für den Betrag eines Vektors: einheitliche Pfeillänge
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Verschiedene_Darstellungsvarianten_Vektor_02.png
In diesem Fall wird durch die Richtung des Pfeils die Richtung der physikalischen Größe angegeben. Die Information zum Betrag ergibt sich einzig und allein aus der Zahl oder der Variablen, die neben dem Pfeil steht.
An dieser Stelle vielleicht ein paar Worte zum Thema Variablen: Werden wie in der Mechanik physikalische Zusammenhänge betrachtet, ist es hilfreich und sinnvoll, die beschreibenden Gleichungen erst einmal mit Variablen aufzustellen. Dies setzt voraus, dass z.B. für die Beträge von Vektoren, aber eben auch für Abstände, zunächst Variablen verwendet werden und nicht gleich Zahlenwerte. Die Zahlenwerte werden erst ganz am Ende eingesetzt. Was ist der Vorteil dieser Vorgehensweise? Der größte Vorteil ist, dass man allgemeingültige Gleichungen für ein System erhält. Man kann also für ein und dasselbe System sehr einfach verschiedene Varianten durchrechnen. Nehmen wir einmal das Beispiel einer Brücke. Aus Ingenieurssicht interessiert z.B. die Beanspruchung der Brückenpfeiler, wenn nicht so viel Verkehr herrscht. Genauso interessant ist aber auch die Belastung zur Rush Hour, wenn fünf Mal so viel Verkehr fließt, also deutlich mehr Gewicht auf den Pfeilern lastet. Stehen die Gleichungen in Form von Variablen zur Verfügung, können unterschiedliche Zahlenwerte für die Belastung einfach eingesetzt und die daraus resultierenden Beanspruchungen der Pfeiler für unterschiedliche Lastszenarien ausgerechnet werden. Genauso einfach könnte überprüft werden, wie es sich auf die Beanspruchung der Pfeiler auswirkt, wenn die Länge der Brücke z.B. um 20% erhöht wird.
Exkurs zum Thema Gleichgewichtsbedingungen
In der Mechanik werden typischer Weise vorzeichenbehaftete Beträge neben dem Vektorpfeil angegeben. Wenn du jetzt denkst, “Moment mal, ein Betrag ist per Definition doch positiv!”, dann hast du natürlich recht. So, wie die Vektoren in der Mechanik zum Beispiel in Freikörperbildern für Kräfte verwendet werden, erhält man durch Auswerten der Gleichgewichtbedingungen aber einen vorzeichenbehafteten Wert. Schauen wir uns das für das dargestellte System mal für die Kraft \(𝐴_𝐻\) genauer an.
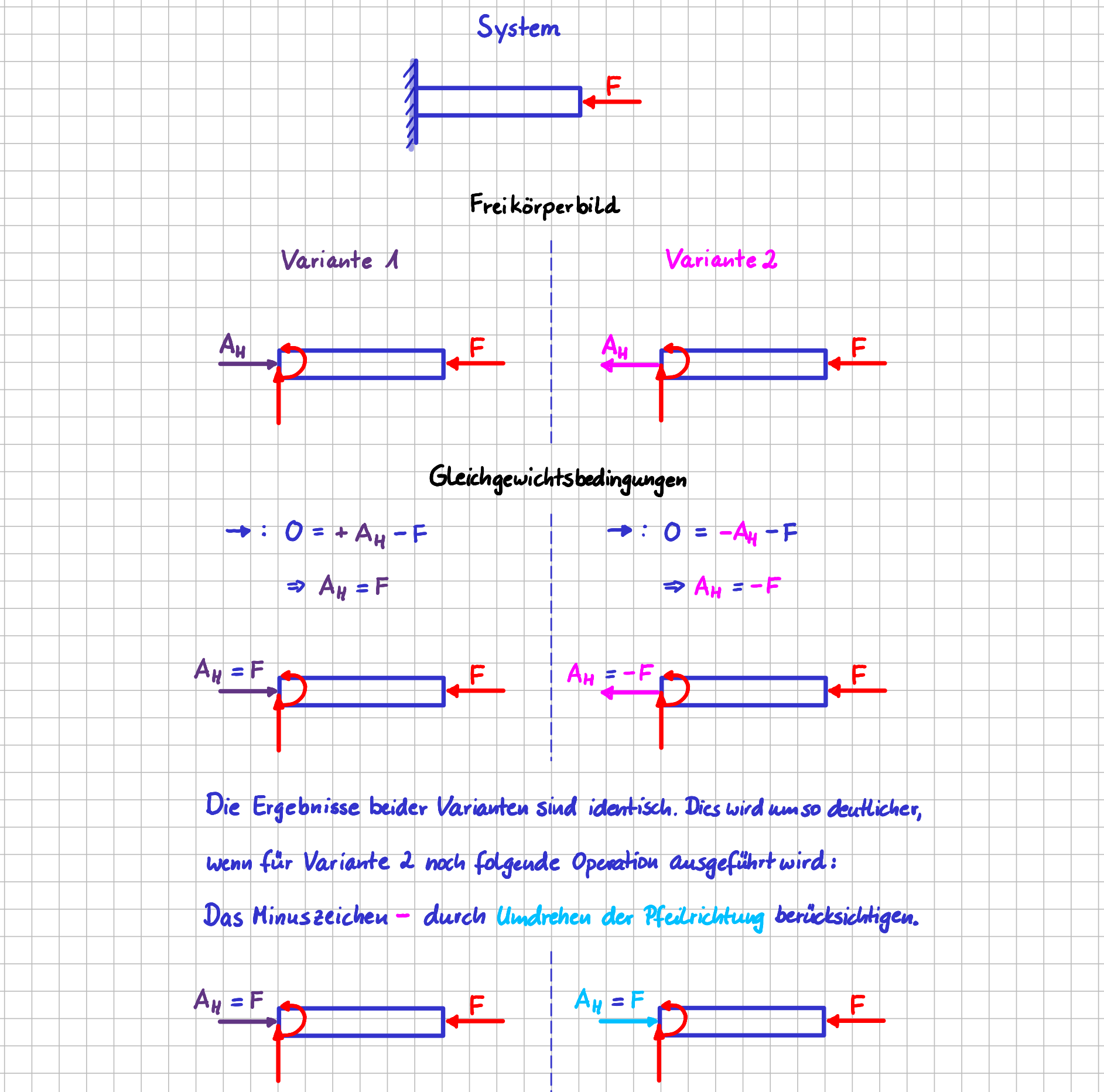
Vorzeichenbehaftete Beträge am Beispiel eines fest eingespannten Balkens
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Vorzeichen_behaftete_Betraege.png
Freikörperbild-Variante 1:
Wird die Kraft beim Freischneiden mit Pfeilspitze "nach rechts" eingezeichnet, ergibt sich aus dem Kräftegleichgewicht in horizontaler Richtung \(A_H=F\).
Freikörperbild-Variante 2:
Wird die Kraft \(A_H\) beim Freischneiden mit Pfeilspitze "nach links" eingezeichnet, ergibt sich aus dem Kräftegleichgewicht in horizontaler Richtung \(A_H=(-F)\).
\(A_H\) hat in beiden Fällen den Betrag \(F\). Und dieser Betrag ist positiv. Das Minuszeichen in der zweiten Variante allerdings zeigt an, dass die Kraft \(A_H\) nicht in die angenommene Pfeilrichtung im Freikörperbild zeigt, sondern in die entgegengesetzte Richtung. Im Vorzeichen ist also noch zusätzlich zum Betrag die Richtungsinformation enthalten. Ergebnisse aus den Gleichgewichtsbedingungen müssen also immer im Zusammenhang mit den gewählten Pfeilrichtungen für die Vektoren im Freikörperbild gesehen werden. Der Ausdruck “Neben dem Vektorpfeil steht der vorzeichenbehaftete Betrag.” ist also die Langform für “Neben dem Vektorpfeil steht der Betrag. Das Vorzeichen davor gibt zusätzlich die Richtungsinformation an: ‘+’ bedeutet in Richtung des eingezeichneten Pfeils, ‘-’ bedeutet entgegen der Richtung des eingezeichneten Pfeils”.
Für Variante 1 und Variante 2 ergibt sich also das identische Ergebnis. Dies war selbstverständlich auch zu erwarten, da es der Physik egal ist, welchen Ansatz wir als diejenigen, die ein Modell erstellen, zur Beschreibung wählen. Das physikalische Prinzip “Statisches System im Gleichgewicht” gilt ja unabhängig von irgendeinem konkreten Beschreibungsansatz.
Für die mathematische Darstellung von Vektoren werden verschiedene Schreibweisen verwendet. Je nach Quelle werden Vektoren fett, mit Unterstrich oder mit einem Pfeil darüber dargestellt. Diese drei Darstellungen beschreiben also ein und denselben Vektor:
$$\mathbf{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\hspace{3cm} \underline{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\hspace{3cm} \vec{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}$$
Auch bei der Wahl der Klammerart gibt es verschiedene Schreibweisen: es werden sowohl runde als auch eckige Klammern verwendet. Um Vektoren auch in einer Zeile schreiben zu können, wird das sogenannte transponiert-Zeichen verwendet.
$$
\underline{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} \qquad \leftrightarrow \qquad \underline{r}=[1\quad 0\quad -1]^T
$$
Zwei Vektoren sind immer dann identisch, wenn sie dieselbe Richtung und denselben Betrag haben, also gleich lang sind. Alle in der folgenden Abbildung gezeigten Vektoren sind daher identisch: $$\vec{a}\ =\ \vec{b}\ =\ \vec{c}\ =\ \vec{d}$$
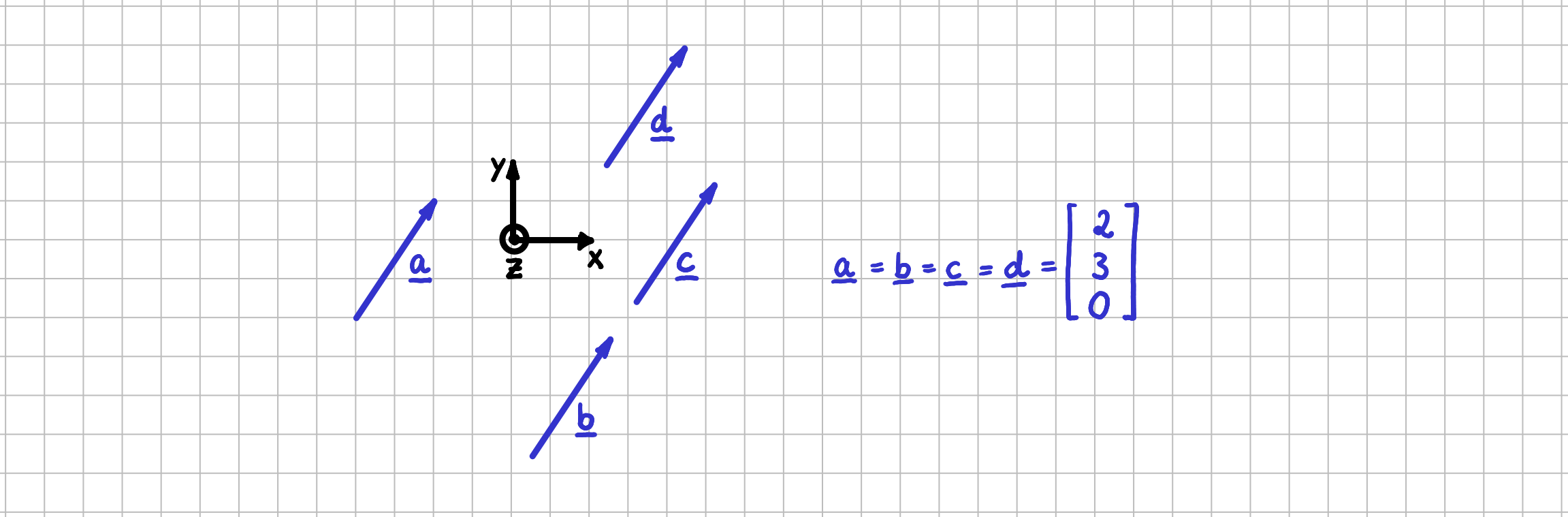
Identische Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Identische_Vektoren.png
Zusammenfassung - Das Wichtigste in Kürze
Darstellungsformen für Vektoren
Es gibt verschiedene Darstellungsformen für Vektoren. Alle folgenden mathematischen Darstellungen sind identisch:
$$\mathbf{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\qquad \underline{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\qquad \vec{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} \qquad\underline{r}=[1\quad 0\quad -1]^T$$
Für die graphische Darstellung wird ein Pfeil verwendet. Neben dem Pfeil steht der vorzeichenbehaftete Betrag.
Das Vorzeichen vor dem Betrag gibt zusätzlich die Richtungsinformation an:
’ + ’ bedeutet in Richtung des eingezeichneten Pfeils,
’ - ’ bedeutet entgegen der Richtung des eingezeichneten Pfeils.
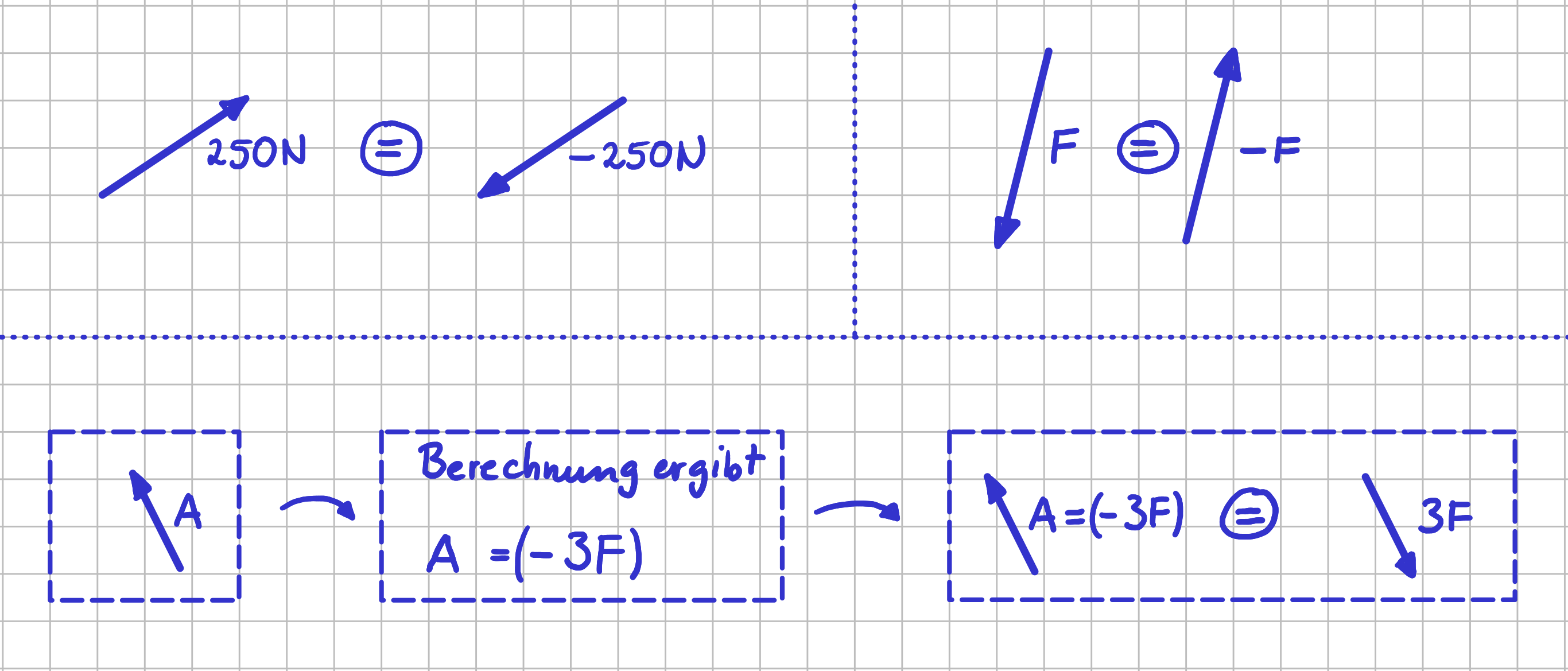
Vorzeichenbehaftete Beträge
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Vorzeichen_behaftete_Betraege_02.png
Aufgabe - Jetzt bist du dran
2.2. Betrag
Betrag eines Vektors
Der Betrag wird auch die Länge eines Vektors genannt und wird mit \(a=\left|\vec{a}\right|\) bezeichnet. Der Betrag eines Vektors \(a\) lässt sich über verschiedene "Denkweisen" bestimmen.
Denkweise 1: geometrische Betrachtung = Satz des Pythagoras
Aus einer geometrischen Betrachtung heraus ergibt sich der Betrag \(a\) über den Satz des Pythagoras direkt zu
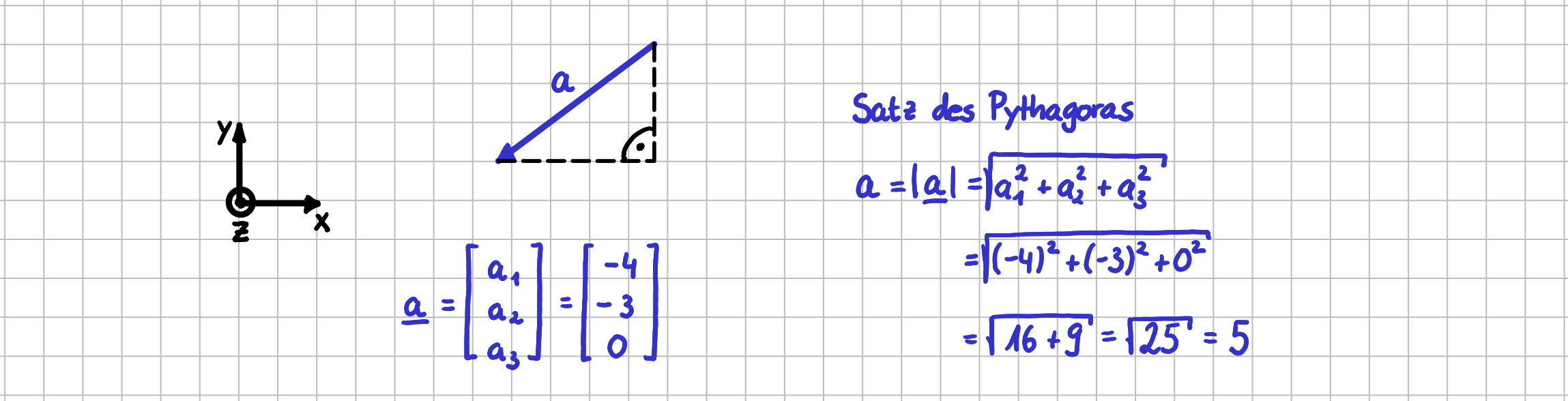
Vektorlänge und Pythagoras
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2144/Verktorlaenge_und_Pythagoras.png
Wird ein Vektor skalar mit sich selber malgenommen, ist der eingeschlossene Winkel 0°, so dass mit \(\cos(0°)=1\) gilt $$\vec{a} \cdot \vec{a} = a \cdot a \cdot \cos(0°)=a^2$$
$$\vec{r}=\begin{pmatrix} 3b \\ 4b \\ 5b \end{pmatrix}$$
$$\mathrm{Pythagoras} \quad \left|\vec{r}\right|=r=\sqrt{(3b)^2+(4b)^2+(5b)^2}=\sqrt{9b^2+16b^2+25b^2}=\sqrt{2 \cdot 25b^2}=5\sqrt{2}b$$
$$\mathrm{Skalarprodukt} \quad \left|\vec{r}\right|=r=\sqrt{\begin{pmatrix} 3b \\ 4b \\ 5 b \end{pmatrix} \cdot \begin{pmatrix} 3b \\ 4b \\5 b \end{pmatrix}}=\sqrt{9b^2+16b^2+25b^2}=\sqrt{2 \cdot 25b^2}=5\sqrt{2}b$$
Zusammenfassung - Das Wichtigste in Kürze
Betrag eines Vektors
Der Betrag eines Vektors gibt die Länge des Vektors an. Er kann mittels des des Satzes von Pythagoras oder mittels des Skalarproduktes berechnet werden:
Arbeitsblatt - Teste dein Wissen
Test - Jetzt bist du dran
2.3. Richtung und normierte Vektoren
Richtung und normierte Vektoren
Wenn du dich für die Richtung eines Vektors interessierst, dann kann es hilfreich sein, wenn du den Einheitsvektor für die durch den Vektor gegebene Richtung kennst. Wenn du diesen normierten Vektors hast, kannst du ihn durch Malnehmen mit einer Zahl beliebig lang machen.
Wenn du den zu einem gegebenen Vektor gehörenden Einheitsvektor bestimmst, dann nennt man diesen Vorgang Normieren.
Wenn ein Vektor normiert wird, dann bedeutet das, dass man ihn so umformt, dass er die Länge \( 1\) hat. Normierte Vektoren werden daher auch als Einsvektoren oder Einheitsvektoren bezeichnet. Bei den Vektoren
$$\vec{e}_x=\begin{pmatrix}1\\0\\0\end{pmatrix},\qquad\vec{e}_y=\begin{pmatrix}0\\1\\0\end{pmatrix},\qquad\vec{e}_z=\begin{pmatrix}0\\1\\0\end{pmatrix}$$
ist offensichtlich, dass es sich um Einheitsvektoren handelt.
Es ist aber möglich, jeden beliebigen Vektor auf die Länge \( 1\) zu bringen. Schauen wir uns das an einem Beispiel an.
Zahlenbeispiel
$$\vec{r}=\begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} \quad \rightarrow \quad \left| \vec{r} \right|=\sqrt{2^2+(-1)^2+3^2}=\sqrt{14} \\\rightarrow \quad \vec{\hat{r}}=\frac{1}{\left| \vec{r} \right|}\vec{r}=\frac{1}{\sqrt{14}}\begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}$$
Der Vektor \(\vec{r}\) hat die Länge \(\sqrt{14}\). Teilen wir den Vektor durch diese Länge, hat er wie gewünscht die Länge \(1\). Normierte Vektoren werden dabei oft auch mit einem "Dach" gekennzeichnet: \(\vec{\hat{r}}\).
Die allgemeine Rechnenvorschrift zur Normierung eines Vektors \(\vec{r}\) lautet also:
$${\vec{\hat{r}}=\frac{1}{\left| \vec{r} \right|}\vec{r}}$$
Ein normierter Vektor hat die Länge \(1\) und zeigt in die Richtung des ursprünglichen Vektors.
Ein normierter Vektor ist immer einheitenlos, da durch den Betrag des Vektors geteilt wird. Und da der Betrag dieselbe Einheit hat, wie die einzelnen Komponenten, kürzen sich die Einheiten weg.
In der Mechanik kommen normierte Vektoren an verschiedenen Stellen zum Einsatz. Wird eine Struktur z.B. von einem Seil abgestützt, so kann die Richtung des Seils, nennen wir sie \(\vec{r}_{\mathrm{Seil}}\) aus der Geometrie berechnet werden. Wird dieser Vektor normiert, liegt ein Vektor mit Länge \(1\) in Richtung der Seilkraft vor: \(\vec{\hat{r}}_{\mathrm{Seil}}\) Die Seilkraft \(\vec{S}\) mit dem Betrag \(S\) lässt sich dann angeben als \(\vec{S}=S \cdot\vec{\hat{r}}_{\mathrm{Seil}}\).
Beispiel
Der Eckpfosten eines Gartenzaunes ist bei Punkt \(A\) fest im Boden verankert. Zusätzlich wird er durch ein Seil, dass die Punkte \(B\) und \(C\) verbindet, gehalten. Der Pfosten wird in Punkt \(B\) durch die Kräfte \(\left| \vec{F}_1 \right| = F\) und \(\left| \vec{F}_2 \right| = F\) belastet. Die Kraft im Seil ist \(\vec{S}\) mit \(\left| \vec{S} \right| = S\).
Die Lage der Punkte \(B\) und \(C\) ist gegeben durch die Vektoren
$$\vec{r}_{AB}=\begin{pmatrix}
0 \\ 0 \\ 2a \end{pmatrix} \quad \mathrm{und} \quad \vec{r}_{AC}=\begin{pmatrix}
-a \\ -a \\ 0 \end{pmatrix}$$
Gesucht ist der Vektor der Seilkraft \(\vec{S}\) .
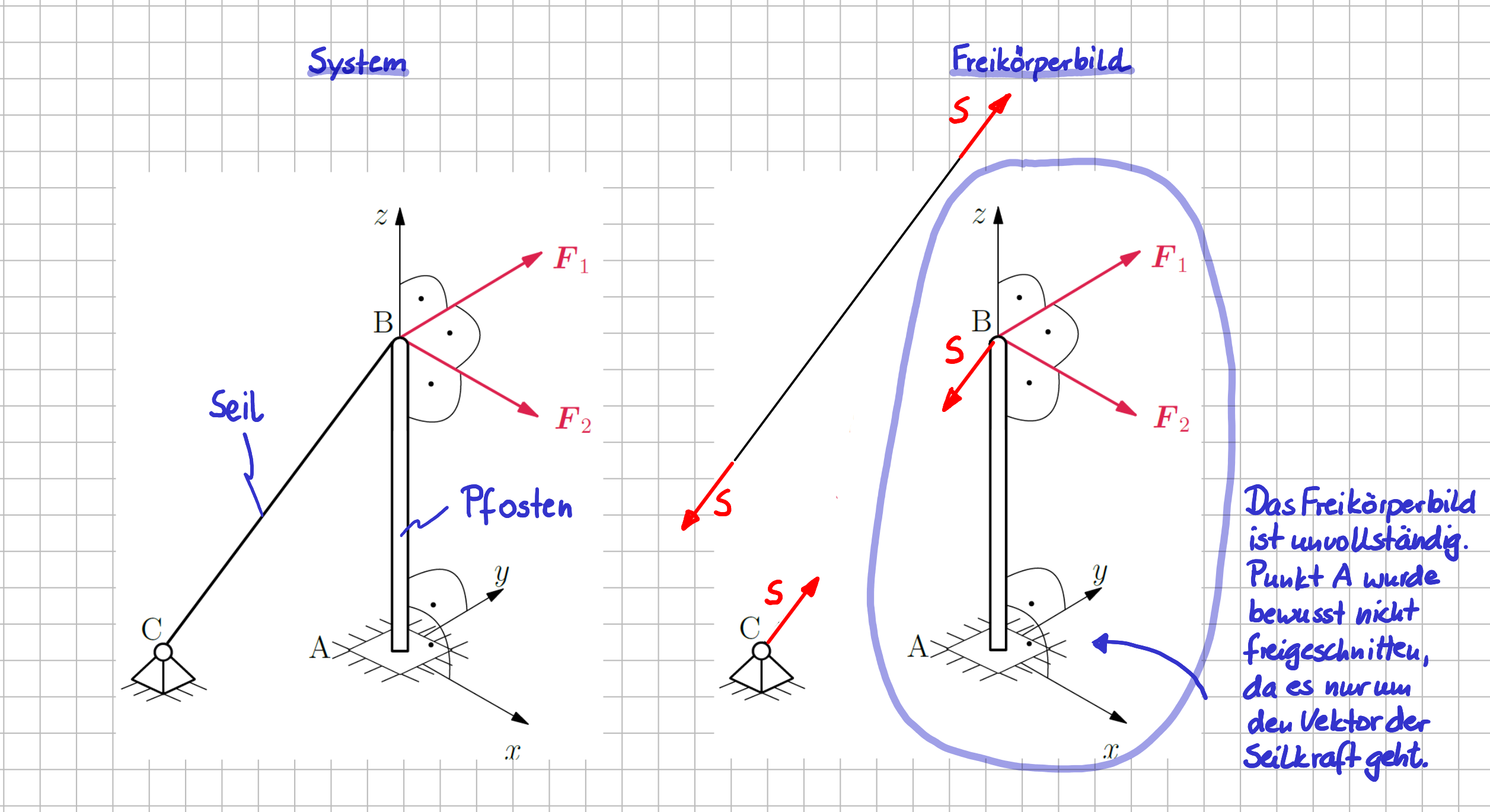
Anwendungsbeispiel: Abstützung eines Pfostens mit einem Seil
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2145/Aanwendungsbeispiel_Abstuetzung_eines_Pfostens.png
$$\vec{S}=S\cdot \vec{\hat{r}}_{BC},$$
da der Betrag \(S\) der Seilkraft ja laut Aufgabenstellung bekannt ist.
Es muss also lediglich der normierte Vektor von \(B\) nach \(C\) bestimmt werden. Es gilt
$$\vec{r}_{BC}=\vec{r}_{AC}-\vec{r}_{AB}=\begin{pmatrix}
-a \\ -a \\ 0 \end{pmatrix}-\begin{pmatrix} 0 \\ 0 \\ 2a
\end{pmatrix}=\begin{pmatrix} -a \\ -a \\ -2a \end{pmatrix}.$$
Die Länge dieses Vektors ergibt sich zu
$$\left| \vec{r}_{BC}\right|=\sqrt{(-a)^2+(-a)^2+(-2a)^2}=\sqrt{6}a.$$
Damit gilt für den normierten Vektor in Richtung von \(B\) nach \(C\)
$$\vec{\hat{r}}_{BC}=\frac{1}{\sqrt{6}a}\cdot \begin{pmatrix} -a \\ -a \\ -2a \end{pmatrix}=\frac{1}{\sqrt{6}}\cdot \begin{pmatrix} -1 \\ -1 \\ -2 \end{pmatrix}.$$
Und für den Vektor \(\vec{S}\) der Seilkraft folgt unter Berücksichtigung der oben bereits aufgestellten Beziehung
$$\vec{S}=S\cdot \vec{\hat{r}}_{BC} = \frac{S}{\sqrt{6}}\begin{pmatrix} -1 \\ -1 \\ -2 \end{pmatrix}.$$
Es ist immer hilfreich, einen Plausibilitätscheck durchzuführen. Die Komponenten des Ergebnisvektors haben die Einheit einer Kraft: Check. Alle Komponenten des Ergebnisvektors sind negativ. Da, wie im Freikörperbild ersichtlich ist, alle Komponenten - in Bezug auf das zugrundegelegte Koordinatensystem - in negative Achsrichtung zeigen, ist das Ergebnis auch in diesem Punkt plausibel: Check.
Das beschriebene Vorgehen lässt sich auch für Stabkräfte in Fachwerken anwenden. Dieser Fall wird in einem der Arbeitsblätter behandelt.
Zusammenfassung - Das Wichtigste in Kürze
Normierter Vektor
$$\quad\vec{\hat{r}}=\dfrac{1}{\left| \vec{r} \right|}\vec{r}$$
Ein normierter Vektor hat die Länge 1 und zeigt in die Richtung des ursprünglichen Vektors. Er wird auch Einsvektor oder Einheitsvektor genannt.
Ein normierter Vektor ist immer einheitenlos, da durch den Betrag des Vektors geteilt wird. Und da der Betrag dieselbe Einheit hat, wie die einzelnen Komponenten, kürzen sich die Einheiten weg.
Ist der Einsvektor in eine bestimmte Richtung bekannt, kann ein beliebiger Vektor, der in diese Richtung zeigt, leicht angegeben werden:
$$\vec{F}=F\cdot \vec{\hat{r}}_{AB}$$
Vektor mit Betrag \(F\) in Richtung der Strecke von Punkt \(A\) nach Punkt \(B\).
Arbeitsblatt - Trainiere deine Fähigkeiten
Aufgabe - Jetzt bist du dran
Test - Prüfe dein Wissen
3. Rechenoperationen
Rechenoperationen für Vektoren
Bei Vektoren handelt es sich um eine andere mathematische Größe als bei einem Skalar. Deshalb ist die Frage, welche Rechenoperationen denn überhaupt definiert sind, sehr sinnvoll.
Die Addition und die Subtraktion sind auch für Vektoren definiert. Die Division, also das Teilen, hingegen nicht. Dafür gibt es gleich zwei Arten, Vektoren miteinander zu multiplizieren. Einmal kommt als Ergebnis der Malrechnung ein Skalar heraus, einmal ein Vektor. Auch kann ein Vektor mit einem Skalar multipliziert werden.
Du siehst also, es ist und bleibt spannend. In den folgenden Abschnitten schauen wir uns die einzelnen Rechenoperationen für Vektoren Schritt für Schritt an.
3.1. Skalierung
Skalierung von Vektoren
Ein Vektor \( \vec{a} \) wird skaliert, indem er mit einer reellen Zahl \( m \) multipliziert wird. Multiplizieren mit einer Zahl wiederum bedeutet, jede einzelne Komponente mit der entsprechenden Zahl malzunehmen:
$${m \cdot \vec{a}=\begin{pmatrix} m \cdot a_1 \\ m \cdot a_2 \\ m \cdot a_3 \end{pmatrix}}$$
Zahlenbeispiel
$$m = 3 \qquad \vec{a}=\begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}\quad \rightarrow \quad m \cdot \vec{a}=\begin{pmatrix} 3 \cdot 2 \\ 3 \cdot (-3) \\ 3 \cdot 5 \end{pmatrix} = \begin{pmatrix} 6 \\ -9 \\ 15 \end{pmatrix}$$
Der Ausgangsvektor wird um den Faktor \(3\) skaliert: Er behält seine Richtung, ändert aber seine Länge auf das Dreifache.
Was passiert für den Fall, dass \(m=(-1)\) gilt?
Zahlenbeispiel
$$m = (-1) \qquad \vec{a}=\begin{pmatrix} 2 \\ 3 \\0 \end{pmatrix} \quad \rightarrow \quad m \cdot \vec{a}= \begin{pmatrix} -2 \\ -3 \\ 0\end{pmatrix}$$
Die Richtung des ursprünglichen Vektors wird durch das Malnehmen mit \((-1)\) also umgekehrt:
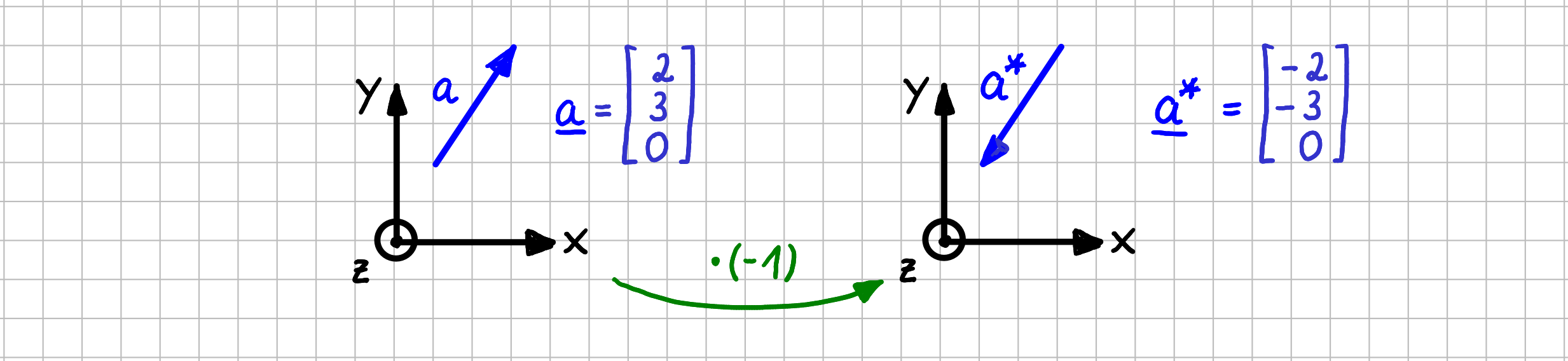
Umkehr der Richtung eines Vektors bei Multiplikation mit (-1)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2147/Umkehr_der_Richtung_eines_Vektors.png
Dieser Aspekt spielt für das Verständnis der Subtraktion eine Rolle. Außerdem ist er auch beim Erstellen von Freikörperbildern und der Bestimmung von Reaktionskräften in der Mechanik von großer Bedeutung.
Zusammenfassung - Das Wichtigste in Kürze
Mahlnehmen mit einer reellen Zahl
$$m \cdot \vec{a}=\begin{pmatrix} m \cdot a_1 \\ m \cdot a_2 \\ m \cdot a_3 \end{pmatrix}$$
Der Ausgangsvektor wird um den Faktor \(m\) skaliert: Er behält seine Richtung, ändert aber seine Länge um den Faktor \(m\).
Insbesondere: Malnehmen mit \(m=(-1)\) bedeutet, dass sich die Richtung des Vektors umkehrt:
$$\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \quad \rightarrow \quad (-1) \cdot \vec{a}=\begin{pmatrix} - a_1 \\ - a_2 \\ - a_3 \end{pmatrix}$$

Umkehr der Richtung eines Vektors bei Multiplikation mit (-1)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2147/Umkehr_der_Richtung_eines_Vektors.png
Arbeitsblatt - Teste dein Wissen
3.2. Addition
Addition von Vektoren
Wenn zwei Vektoren \(\vec{a}\) und \(\vec{b}\) addiert werden, ist das Ergebnis wieder ein Vektor. Dies sei \(\vec{c}\) . Die Komponenten von \(\vec{c}\) ergeben sich, indem die Komponenten von \(\vec{a}\) und \(\vec{b}\) einzeln addiert werden.
$$\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \qquad\vec{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \quad \rightarrow \quad {\vec{a}+\vec{b}=\begin{pmatrix} a_1+b_1 \\ a_2+b_2 \\ a_3+b_3 \end{pmatrix} =\vec{c}}$$
Zahlenbeispiel
$$\vec{a}=\begin{pmatrix} 3 \\ -2 \\ 5 \end{pmatrix} \qquad\vec{b}=\begin{pmatrix} 0 \\ 8 \\ -7 \end{pmatrix} \quad \rightarrow \quad\vec{a}+\vec{b}=\begin{pmatrix} 3+0 \\ -2+8 \\ 5-7 \end{pmatrix} =\begin{pmatrix} 3 \\ 6 \\ -2 \end{pmatrix}$$
Anschaulich bedeutet dies Folgendes. Stell dir vor, du bist in der Stadt und befindest Dich am Punkt \(S\) und willst zu einem Sportgeschäft, dass sich beim Punkt \(E\) befindet. Du fragst jemanden nach dem Weg und bekommst folgende Antwort: "Lauf die Straße nach südsüdost bis sie einen Knick macht. Dann folge der Straße weiter in Richtung südsüdwest, bis du nach ca. 250m das Sportgeschäft erreichst."
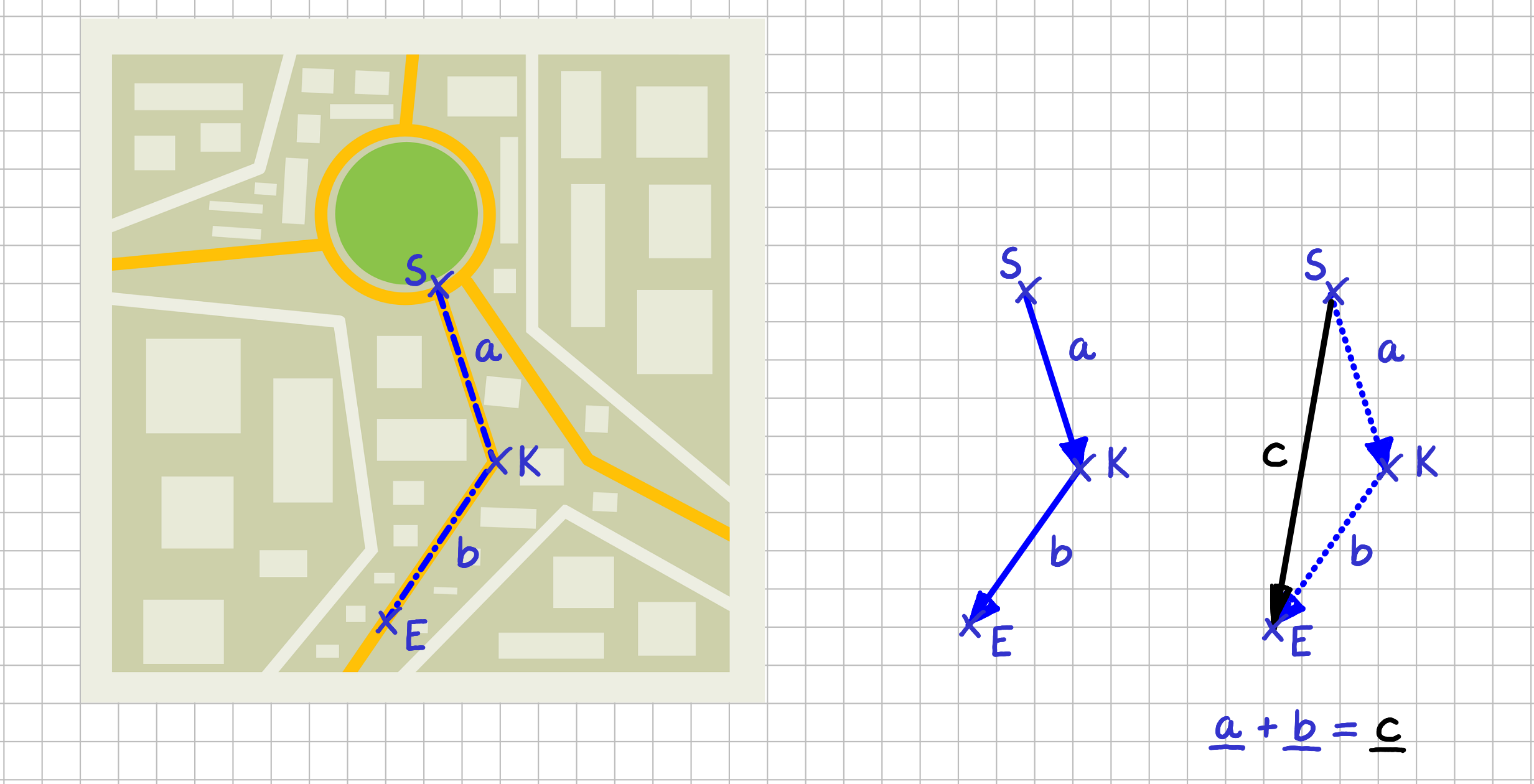
Addition von Vektoren im Alltag
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2146/Addition_von_Vektoren_im_Alltag.png
Wenn du zufällig einen Mathematiker nach dem Weg gefragt hättest, hätte er dir gesagt: "Folge zuerst dem Vektor \(\vec{a}\) . Anschließend folge dem Vektor \(\vec{b}\) ". Beide Aussagen sind identisch. Denn wenn du vor dem Sportgeschäft bei Punkt \(E\) stehst und Dich fragst, "Wie weit bin ich denn nun eigentlich von meinem Startpunkt entfernt, dann ist die Antwort, "Genau die Länge des Vektors \(\vec{c}\) ". Vektor \(\vec{c}\) entsteht, indem man die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) hintereinandersetzt. Vektor \(\vec{c}\) ergibt sich dann als resultierender Vektor der beiden Einzelvektoren.
Noch ein Beispiel, diesmal mit Kräften. Stell dir vor, ein Auto hat sich im Sand oder im Matsch festgefahren. In Richtung der Hauptachse des Fahrzeugs muss die Kraft \(F\) aufgebracht werden, um das Fahrzeug wieder freizuschleppen. Jetzt, wo du schon einiges über Vektoren weißt, hast du verschiedene Möglichkeiten. Du kannst z.B. mit einer Seilwinde direkt die Kraft \(F\) in Richtung der Hauptachse aufbringen. Was aber machst du, wenn eine Seilwinde nicht die erforderliche Kraft \(F\) aufbringen kann? Du nimmst einfach zwei Seilwinden, die ihre Kräfte \(F_1\) und \(F_2\) platzbedingt natürlich nur unter einem gewissen Winkel aufbringen können. Solange die beiden Kräfte und Kraftrichtungen so eingestellt werden, dass sich als resultierende Kraft eine Kraft mit Betrag \(F\) entlang der Fahrzeughauptachse ergibt, bekommst du das festgefahrene Fahrzeug auch auf diese Art freigeschleppt. Jede der beiden Seilwinden muss dabei nur eine Kraft aufbringen, die deutlich geringer als die Gesamtkraft \(F\) ist.
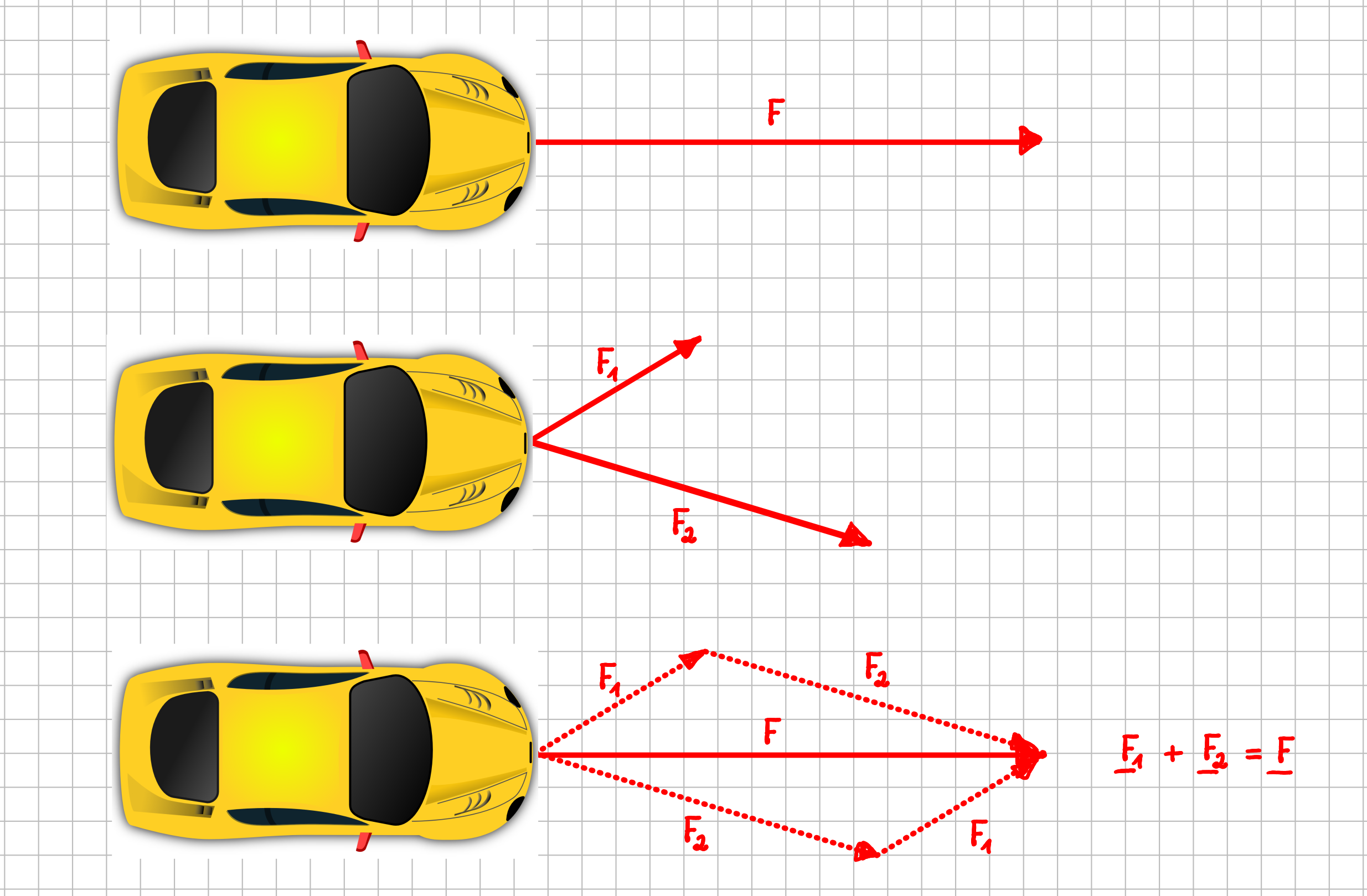
Anwenden der Vektoraddition beim Freischleppen eines Fahrzeugs
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2146/Anwenden_der_Vektoraddition_beim_Freischleppen.png
Wie sich aus den anschaulichen Beispielen aber auch aus den mathematischen Beziehungen sofort ergibt, ist die Addition zweier Vektoren vertauschbar. Es gilt also
$${\vec{a} + \vec{b} = \vec{b} + \vec{a}}$$
Für die Lateinfreaks: Das Kommutativgesetz gilt auch bei der Addition von Vektoren.
Zusammenfassung - Das Wichtigste in Kürze
Addition von Vektoren
Wenn zwei Vektoren \(\vec{a}\) und \(\vec{b}\) addiert werden, ist das Ergebnis wieder ein Vektor. Dies sei \(\vec{c}\) . Die Komponenten von \(\vec{c}\) ergeben sich, indem die Komponenten von \(\vec{a}\) und \(\vec{b}\) einzeln addiert werden.
$$\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \qquad\vec{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \quad \rightarrow \quad \vec{a}+\vec{b}=\begin{pmatrix} a_1+b_1 \\ a_2+b_2 \\ a_3+b_3 \end{pmatrix} =\vec{c}$$
Bei der Addition von Vektoren ist die Reihenfolge vertauschbar, d.h. es gilt das Kommutativgesetz.
$$\vec{a} + \vec{b} = \vec{b} + \vec{a}$$
Graphisch lässt sich die Addition als "Hintereinanderschaltung" der beiden Vektoren verstehen
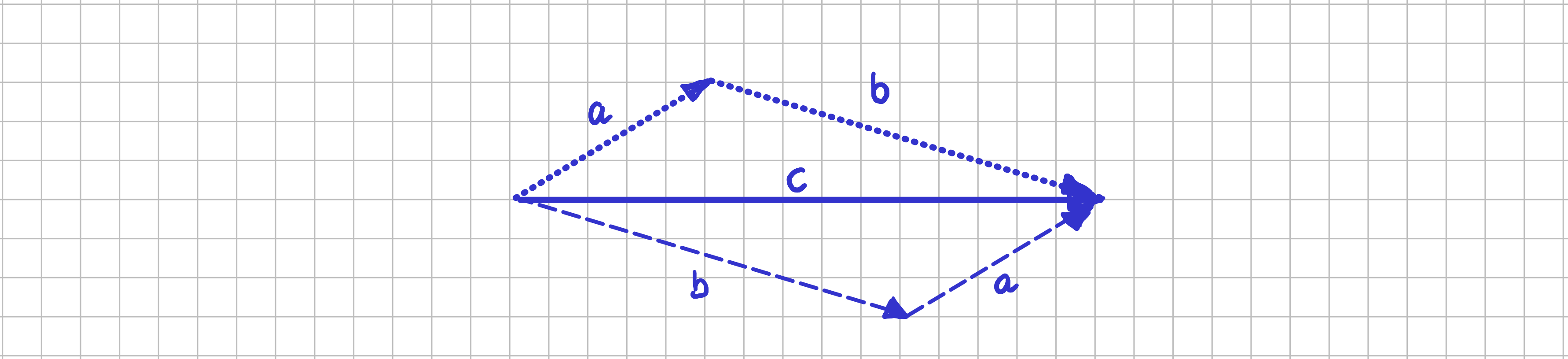
Addition von Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://writemd.rz.tuhh.de/uploads/a8e868b3e0e3a27307fed831c.png
Arbeitsblatt - Teste dein Wissen
Test - Jetzt bist du dran
3.3. Subtraktion
Subtraktion von Vektoren
Die Subtraktion zweier Vektoren \( \vec{d} \) und \( \vec{e} \) wird analog zur Addition ausgeführt und liefert ebenfalls einen Vektor als Ergebnis. Dies sei \( \vec{f} \) $$ \vec{d}=\begin{pmatrix} d_1 \\ d_2 \\ d_3 \end{pmatrix} \qquad \vec{e}=\begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix} \quad \rightarrow \quad {\vec{d}-\vec{e}=\begin{pmatrix} d_1-e_1 \\ d_2-e_2 \\ d_3-e_3 \end{pmatrix} =\vec{f}} $$
Zahlenbeispiel
$$ \vec{d}=\begin{pmatrix} 7 \\ 2 \\ -4 \end{pmatrix} \qquad \vec{e}=\begin{pmatrix} -3 \\ 2 \\ 8 \end{pmatrix} \quad \rightarrow \quad\vec{d}-\vec{e}=\begin{pmatrix} 7-(-3) \\ 2-2 \\ -4-6 \end{pmatrix} =\begin{pmatrix} 10 \\ 0 \\ -12 \end{pmatrix} $$
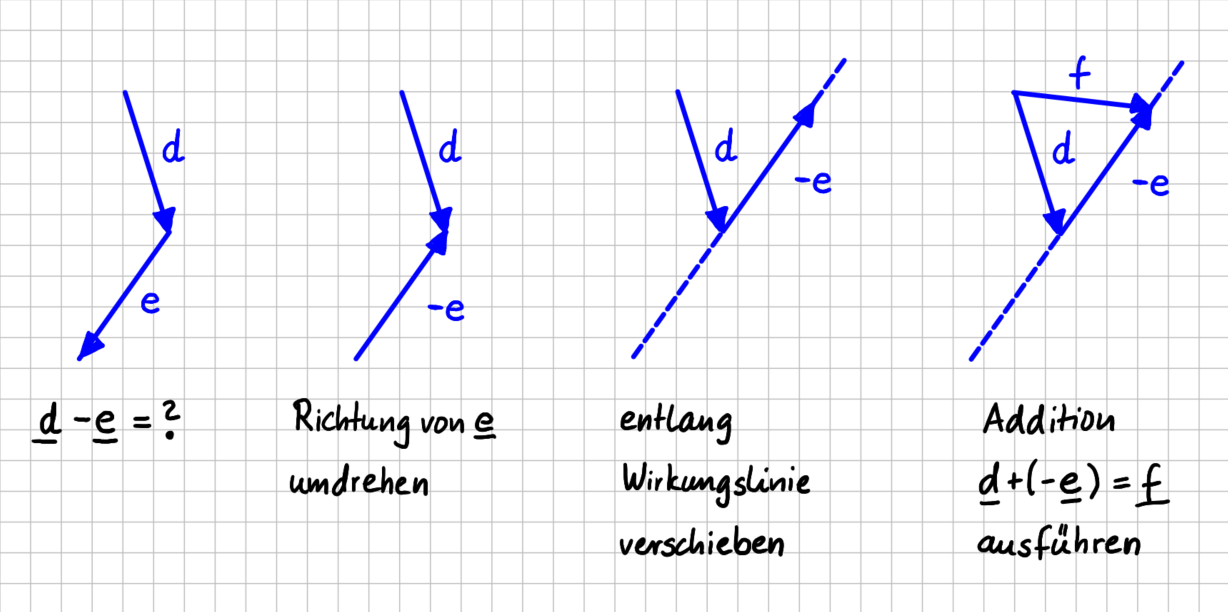
Subtraktion von Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2148/Subtraktion_von_Vektoren.png
Zusammenfassung - Das Wichtigste in Kürze
Subtraktion von Vektoren
Wenn zwei Vektoren \(\vec{d}\) und \(\vec{e}\) von einander abgezogen werden, ist das Ergebnis wieder ein Vektor. Dies sei \(\vec{f}\) . Die Komponenten von \(\vec{f}\) ergeben sich, indem die Komponenten von \(\vec{d}\) und \(\vec{e}\) einzeln voneinander abgezogen werden.
$$\vec{d}=\begin{pmatrix} d_1 \\ d_2 \\ d_3 \end{pmatrix} \qquad\vec{e}=\begin{pmatrix} e_1 \\ e_2 \\ e_3 \end{pmatrix} \quad \rightarrow \quad {\vec{d}-\vec{e}=\begin{pmatrix} d_1-e_1 \\ d_2-e_2 \\ d_3-e_3 \end{pmatrix} =\vec{f}}$$
Bei der Subtraktion von Vektoren ist die Reihenfolge nicht vertauschbar, d.h. das Kommutativgesetz gilt nicht:
$$\vec{d} - \vec{e} \neq \vec{e} - \vec{d}$$
Graphisch lässt sich die Subtraktion ebenfalls als "Hintereinanderschaltung" der beiden Vektoren verstehen, wenn in einem Vorabschritt die Richtung des abzuziehenden Vektors umgedreht wird:

Subtraktion von Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2148/Subtraktion_von_Vektoren.png
Test - Jetzt bist du dran
3.4. Division
Division von Vektoren
Hinweis - Eine Randnotiz zum Verstehen
Don't even think about it!
Die Rechenoperation des Teilens gibt es bei Vektoren schlicht und einfach nicht. Also: bitte gar nicht erst auf die Idee kommen, durch einen Vektor zu teilen.
3.5. Vektorprodukt
Vektorprodukt für Vektoren
Für Vektoren sind zwei Arten von Produkten definiert: das Vektorprodukt, das auch Kreuzprodukt genannt wird, und das Skalarprodukt.
Wie der Name schon klarstellt, ist das Ergebnis des Vektorproduktes wieder ein Vektor; das Ergebnis des Skalarproduktes ist hingegen kein Vektor, sondern ein Skalar, also eine Zahl.
Werden zwei Vektoren \(\vec{a}\) und \(\vec{b}\) mittels Kreuzprodukt miteinander verrechnet, ergibt sich wieder ein Vektor. Nennen wir ihn Vektor \(\vec{c}\) . Vektor \(\vec{c}\) steht senkrecht auf den beiden Ausgangsvektoren.
Mit der Rechten-Hand-Regel lässt sich dabei leicht überprüfen, in welche Richtung \(\vec{c}\) zeigt: der Daumen der rechten Hand wird in Richtung des ersten Vektors, hier \(\vec{a}\) gestreckt, der Zeigefinger in Richtung des zweiten Vektors, hier \(\vec{b}\) . Die Richtung von \(\vec{c}\) ist dann identisch mit der Richtung des angewinkelten Mittelfingers.

Rechte-Hand-Regel beim Kreuzprodukt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2150/Rechte_Hand_Regel_beim_Kreuzprodukt.png
Beim Kreuzprodukt ist die Reihenfolge der beiden Ausgangsvektoren wichtig, d.h. das Kommutativgesetz gilt nicht:
$${\vec{a} \times \vec{b} = -\vec{b} \times \vec{a}}$$
Dies lässt sich auch leicht mit der Rechten-Hand-Regel überprüfen.
Es gibt eine einfache Merkregel für die Berechnung des Kreuzproduktes zweier Vektoren:
Schritt 1: Schreibe die beiden Vektoren zweimal untereinander.
Schritt 2: Streiche die erste und die letzte Zeile.
Schritt 3: Nimm über kreuz mal (daher auch der Name) und ziehe das zweite Produkt vom ersten ab.
Dieses Vorgehen ist hier veranschaulicht:

Schrittweises Vorgehen beim Berechnen des Kreuzproduktes
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2150/Schrittweises_Vorgehen_beim_Berechnen_des_Kreuzproduktes.png
Der Betrag \(\left| \vec{c} \right|\) von \(\vec{c}\) lässt sich neben den bekannten Berechnungsvorschriften auch berechnen über:
$$\left|\vec{c}\right| = \left|\vec{a} \times \vec{b}\right| = ab \sin(\varphi)$$
\(\varphi\) ist der zwischen den beiden Vektoren eingeschlossene Winkel und wird von \(\vec{a}\) aus mathematisch positiv gemessen.
Geometrisch betrachtet ist der Betrag des resultierenden Vektors identisch mit dem Wert des Flächeninhalts, des von den beiden Vektoren \(\vec{a}\) und \(\vec{b}\) aufgespannten Parallelogramms:

Betrag des Ergebnisvektors beim Kreuzprodukt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2150/Betrag_des_Ergebnisvektors_beim_Kreuzprodukt.png
Zusammenfassung - Das Wichtigste in Kürze
Vektorprodukt = Kreuzprodukt
Das Ergebnis des Vektorproduktes zweier Vektoren ist wieder ein Vektor. Der Ergebnisvektor wird nach der folgenden Rechenvorschrift berechnet:

Rechenvorschrift für das Kreuzprodukt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://writemd.rz.tuhh.de/uploads/a8e868b3e0e3a27307fed831f.png
Dann lässt sich der Betrag nach den bekannten Vorschriften (Stichwort 'Pythagoras' oder 'Skalarprodukt') berechnen. Alternativ kann der Betrag auch über die eingeschlossene Fläche der Raute berechnet werden.

Betrag des Ergebnisvektors beim Kreuzprodukt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2150/Betrag_des_Ergebnisvektors_beim_Kreuzprodukt.png
Die Richtung des Ergebnisvektors lässt sich - auch vorab - mit der Rechten-Hand-Regel bestimmen.

Rechte-Hand-Regel beim Kreuzprodukt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2150/Rechte_Hand_Regel_beim_Kreuzprodukt.png
Das Kommutativgesetz gilt für das Kreuzprodukt nicht, d.h. die Reihenfolge der Vektoren kann nicht vertauscht werden. Es gilt stattdessen, wie sich mit der Rechten-Hand-Regel auch leicht prüfen lässt.
$$\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$$
Arbeitsblatt - Teste dein Wissen
Aufgabe - Jetzt bist du dran
Test - Jetzt bist du dran
3.6. Skalarprodukt
Skalarprodukt für Vektoren
Für Vektoren sind zwei Arten von Produkten definiert: das Vektorprodukt, das auch Kreuzprodukt genannt wird, und das Skalarprodukt.
Anders als beim Vektorprodukt ist das Ergebnis des Skalarproduktes ein Skalar, also eine Zahl.
Diese Zahl berechnet sich nach folgender Vorschrift:
$${\vec{a}\cdot\vec{b}=a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3}$$
Werden zwei Vektoren skalar miteinander malgenommen, so errechnet sich das Ergebnis also als Summe der Produkte der Komponenten.
Zahlenbeispiel
$$\begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} -4 \\ 6 \\ 2 \end{pmatrix}=(-2) \cdot (-4) + 1 \cdot 6 + 3 \cdot 2 =20$$
Die Reihenfolge der Vektoren kann beim Skalarprodukt vertauscht werden: Es gilt das Kommutativgesetz
$${\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}}$$
Definiert ist das Skalarprodukt mithilfe des Winkels, den die beiden Vektoren, die miteinander multipliziert werden, einschließen. Dabei wird der Winkel mathematisch positiv, also gegen den Uhrzeigersinn, vom ersten zum zweiten Vektor abgetragen.

Zwischen zwei Vektoren eingeschlossener Winkel
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2152/Zwischen_zwei_Vektoren_eingeschlossener_Winkel.png
$$\vec{a} \cdot \vec{b} := ab\cdot \cos(\varphi)$$
\(a\) und \(b\) sind hierbei die Beträge, also die Längen der beiden Vektoren.
Soll der Winkel zwischen zwei gegebenen Vektoren bestimmt werden, so ist dies nach Umstellen dieser Beziehung leicht möglich:
$$\cos(\varphi)=\frac{\vec{a} \cdot \vec{b}}{ab}$$
Auch lässt sich leicht prüfen, ob zwei Vektoren senkrecht aufeinander stehen, also orthogonal sind. Der eingeschlossene Winkel zweier senkrecht aufeinanderstehender Vektoren ist \(\varphi = 90°\). Und da \(\cos(\varphi = 90°) =0\) gilt, ist auch das Skalarprodukt in diesem Fall Null.
$${\vec{a} \cdot \vec{b} = 0 \qquad \leftrightarrow \qquad \vec{a} \perp \vec{b}}$$
Ergibt das Skalarprodukt zweier Vektoren den Wert Null, stehen die Vektoren senkrecht aufeinander.
Zusammenfassung - Das Wichtigste in Kürze
Skalarprodukt
Das Ergebnis des Skalarproduktes zweier Vektoren ist eine Zahl. Diese Zahl wird nach der folgenden Rechenvorschrift berechnet:
$$\vec{a}\cdot\vec{b}=a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3$$
Werden zwei Vektoren skalar miteinander malgenommen, so errechnet sich das Ergebnis also als Summe der Produkte der Komponenten.
Das Kommutativgesetz gilt für das Skalarprodukt, d.h. die Reihenfolge der Vektoren kann vertauscht werden:
$$\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$$
Alternativ lässt sich das Ergebnis auch über die Beträge der beiden Vektoren und den eingeschlossenen Winkel bestimmen
$$\vec{a} \cdot \vec{b} = ab\cdot \cos(\varphi)$$
Für den Winkel zwischen zwei gegebenenVektoren gilt also:
$$\cos(\varphi)=\frac{\vec{a} \cdot \vec{b}}{ab}$$
Stehen zwei Vektoren senkrecht aufeinander, sind also orthogonal zueinander, ist das Skalarprodukt null
$$\vec{a} \cdot \vec{b} = 0 \qquad \leftrightarrow \qquad \vec{a} \perp \vec{b}$$

 Berechne den Betrag eines Vektors
Berechne den Betrag eines Vektors