Vektorrechnung
Vektorrechnung
3. Rechenoperationen
3.1. Skalierung
Skalierung von Vektoren
Ein Vektor \( \vec{a} \) wird skaliert, indem er mit einer reellen Zahl \( m \) multipliziert wird. Multiplizieren mit einer Zahl wiederum bedeutet, jede einzelne Komponente mit der entsprechenden Zahl malzunehmen:
$${m \cdot \vec{a}=\begin{pmatrix} m \cdot a_1 \\ m \cdot a_2 \\ m \cdot a_3 \end{pmatrix}}$$
Zahlenbeispiel
$$m = 3 \qquad \vec{a}=\begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}\quad \rightarrow \quad m \cdot \vec{a}=\begin{pmatrix} 3 \cdot 2 \\ 3 \cdot (-3) \\ 3 \cdot 5 \end{pmatrix} = \begin{pmatrix} 6 \\ -9 \\ 15 \end{pmatrix}$$
Der Ausgangsvektor wird um den Faktor \(3\) skaliert: Er behält seine Richtung, ändert aber seine Länge auf das Dreifache.
Was passiert für den Fall, dass \(m=(-1)\) gilt?
Zahlenbeispiel
$$m = (-1) \qquad \vec{a}=\begin{pmatrix} 2 \\ 3 \\0 \end{pmatrix} \quad \rightarrow \quad m \cdot \vec{a}= \begin{pmatrix} -2 \\ -3 \\ 0\end{pmatrix}$$
Die Richtung des ursprünglichen Vektors wird durch das Malnehmen mit \((-1)\) also umgekehrt:
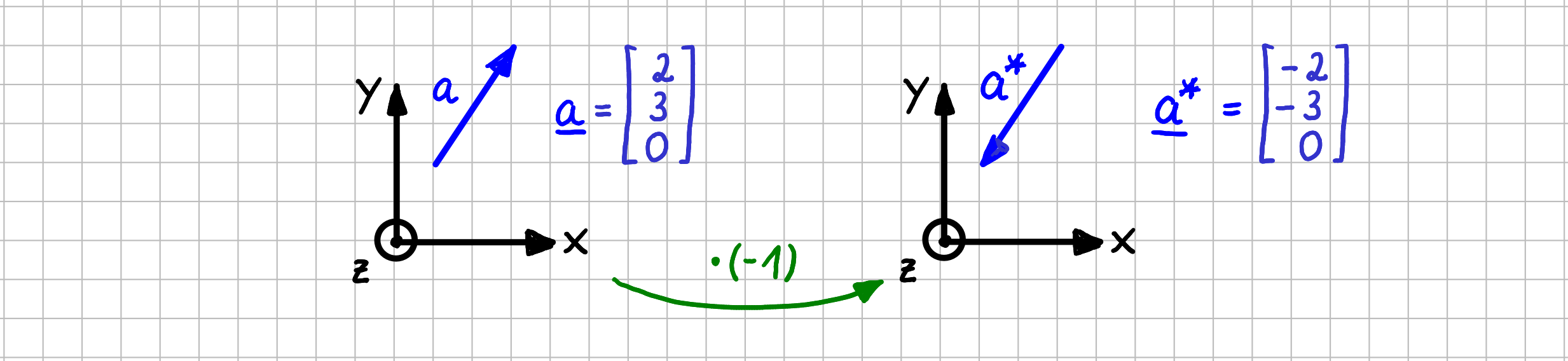
Umkehr der Richtung eines Vektors bei Multiplikation mit (-1)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2147/Umkehr_der_Richtung_eines_Vektors.png
Dieser Aspekt spielt für das Verständnis der Subtraktion eine Rolle. Außerdem ist er auch beim Erstellen von Freikörperbildern und der Bestimmung von Reaktionskräften in der Mechanik von großer Bedeutung.
Zusammenfassung - Das Wichtigste in Kürze
Mahlnehmen mit einer reellen Zahl
$$m \cdot \vec{a}=\begin{pmatrix} m \cdot a_1 \\ m \cdot a_2 \\ m \cdot a_3 \end{pmatrix}$$
Der Ausgangsvektor wird um den Faktor \(m\) skaliert: Er behält seine Richtung, ändert aber seine Länge um den Faktor \(m\).
Insbesondere: Malnehmen mit \(m=(-1)\) bedeutet, dass sich die Richtung des Vektors umkehrt:
$$\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \quad \rightarrow \quad (-1) \cdot \vec{a}=\begin{pmatrix} - a_1 \\ - a_2 \\ - a_3 \end{pmatrix}$$

Umkehr der Richtung eines Vektors bei Multiplikation mit (-1)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2147/Umkehr_der_Richtung_eines_Vektors.png
