Vektorrechnung
Vektorrechnung
3. Rechenoperationen
3.2. Addition
Addition von Vektoren
Wenn zwei Vektoren \(\vec{a}\) und \(\vec{b}\) addiert werden, ist das Ergebnis wieder ein Vektor. Dies sei \(\vec{c}\) . Die Komponenten von \(\vec{c}\) ergeben sich, indem die Komponenten von \(\vec{a}\) und \(\vec{b}\) einzeln addiert werden.
$$\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \qquad\vec{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \quad \rightarrow \quad {\vec{a}+\vec{b}=\begin{pmatrix} a_1+b_1 \\ a_2+b_2 \\ a_3+b_3 \end{pmatrix} =\vec{c}}$$
Zahlenbeispiel
$$\vec{a}=\begin{pmatrix} 3 \\ -2 \\ 5 \end{pmatrix} \qquad\vec{b}=\begin{pmatrix} 0 \\ 8 \\ -7 \end{pmatrix} \quad \rightarrow \quad\vec{a}+\vec{b}=\begin{pmatrix} 3+0 \\ -2+8 \\ 5-7 \end{pmatrix} =\begin{pmatrix} 3 \\ 6 \\ -2 \end{pmatrix}$$
Anschaulich bedeutet dies Folgendes. Stell dir vor, du bist in der Stadt und befindest Dich am Punkt \(S\) und willst zu einem Sportgeschäft, dass sich beim Punkt \(E\) befindet. Du fragst jemanden nach dem Weg und bekommst folgende Antwort: "Lauf die Straße nach südsüdost bis sie einen Knick macht. Dann folge der Straße weiter in Richtung südsüdwest, bis du nach ca. 250m das Sportgeschäft erreichst."
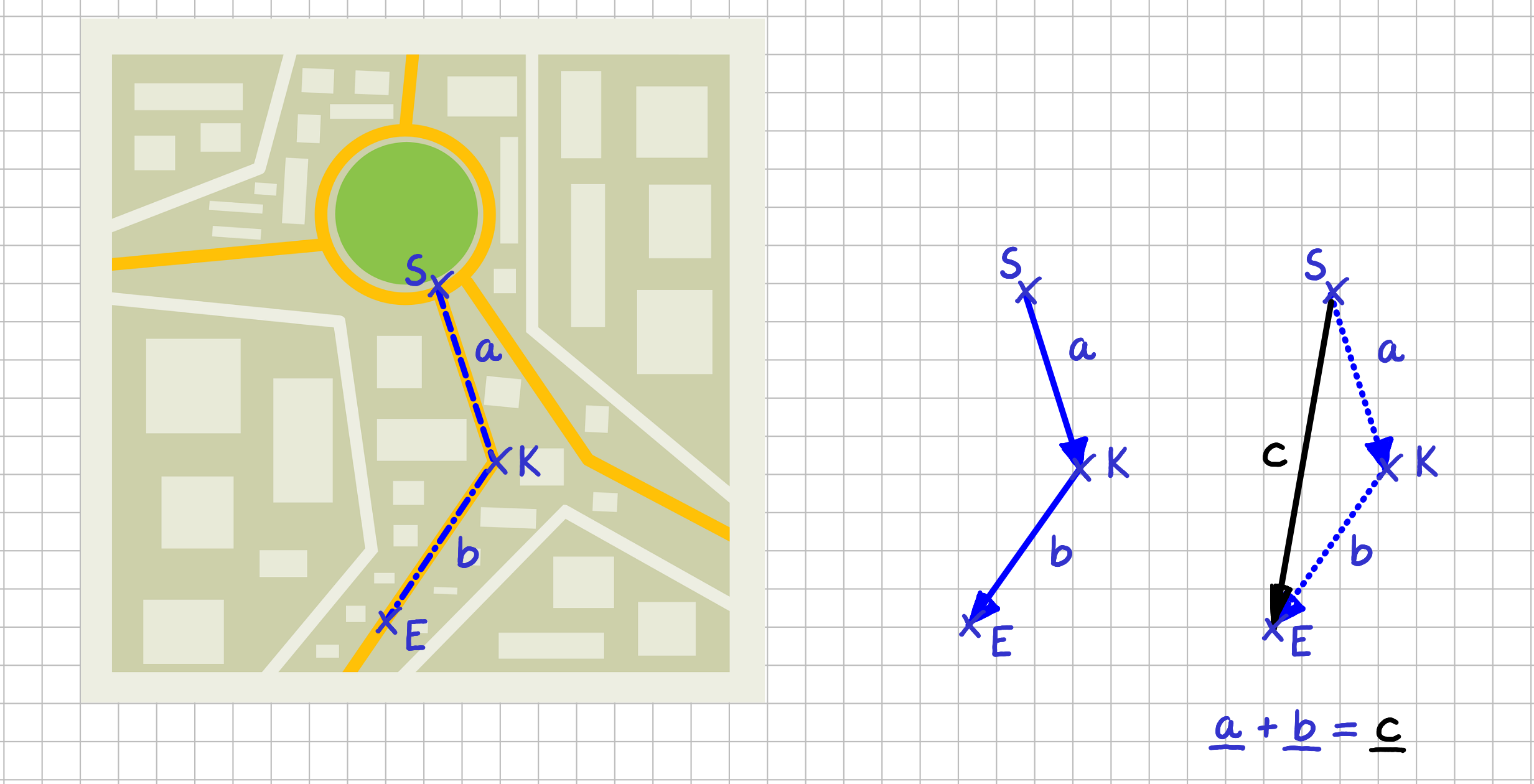
Addition von Vektoren im Alltag
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2146/Addition_von_Vektoren_im_Alltag.png
Wenn du zufällig einen Mathematiker nach dem Weg gefragt hättest, hätte er dir gesagt: "Folge zuerst dem Vektor \(\vec{a}\) . Anschließend folge dem Vektor \(\vec{b}\) ". Beide Aussagen sind identisch. Denn wenn du vor dem Sportgeschäft bei Punkt \(E\) stehst und Dich fragst, "Wie weit bin ich denn nun eigentlich von meinem Startpunkt entfernt, dann ist die Antwort, "Genau die Länge des Vektors \(\vec{c}\) ". Vektor \(\vec{c}\) entsteht, indem man die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) hintereinandersetzt. Vektor \(\vec{c}\) ergibt sich dann als resultierender Vektor der beiden Einzelvektoren.
Noch ein Beispiel, diesmal mit Kräften. Stell dir vor, ein Auto hat sich im Sand oder im Matsch festgefahren. In Richtung der Hauptachse des Fahrzeugs muss die Kraft \(F\) aufgebracht werden, um das Fahrzeug wieder freizuschleppen. Jetzt, wo du schon einiges über Vektoren weißt, hast du verschiedene Möglichkeiten. Du kannst z.B. mit einer Seilwinde direkt die Kraft \(F\) in Richtung der Hauptachse aufbringen. Was aber machst du, wenn eine Seilwinde nicht die erforderliche Kraft \(F\) aufbringen kann? Du nimmst einfach zwei Seilwinden, die ihre Kräfte \(F_1\) und \(F_2\) platzbedingt natürlich nur unter einem gewissen Winkel aufbringen können. Solange die beiden Kräfte und Kraftrichtungen so eingestellt werden, dass sich als resultierende Kraft eine Kraft mit Betrag \(F\) entlang der Fahrzeughauptachse ergibt, bekommst du das festgefahrene Fahrzeug auch auf diese Art freigeschleppt. Jede der beiden Seilwinden muss dabei nur eine Kraft aufbringen, die deutlich geringer als die Gesamtkraft \(F\) ist.
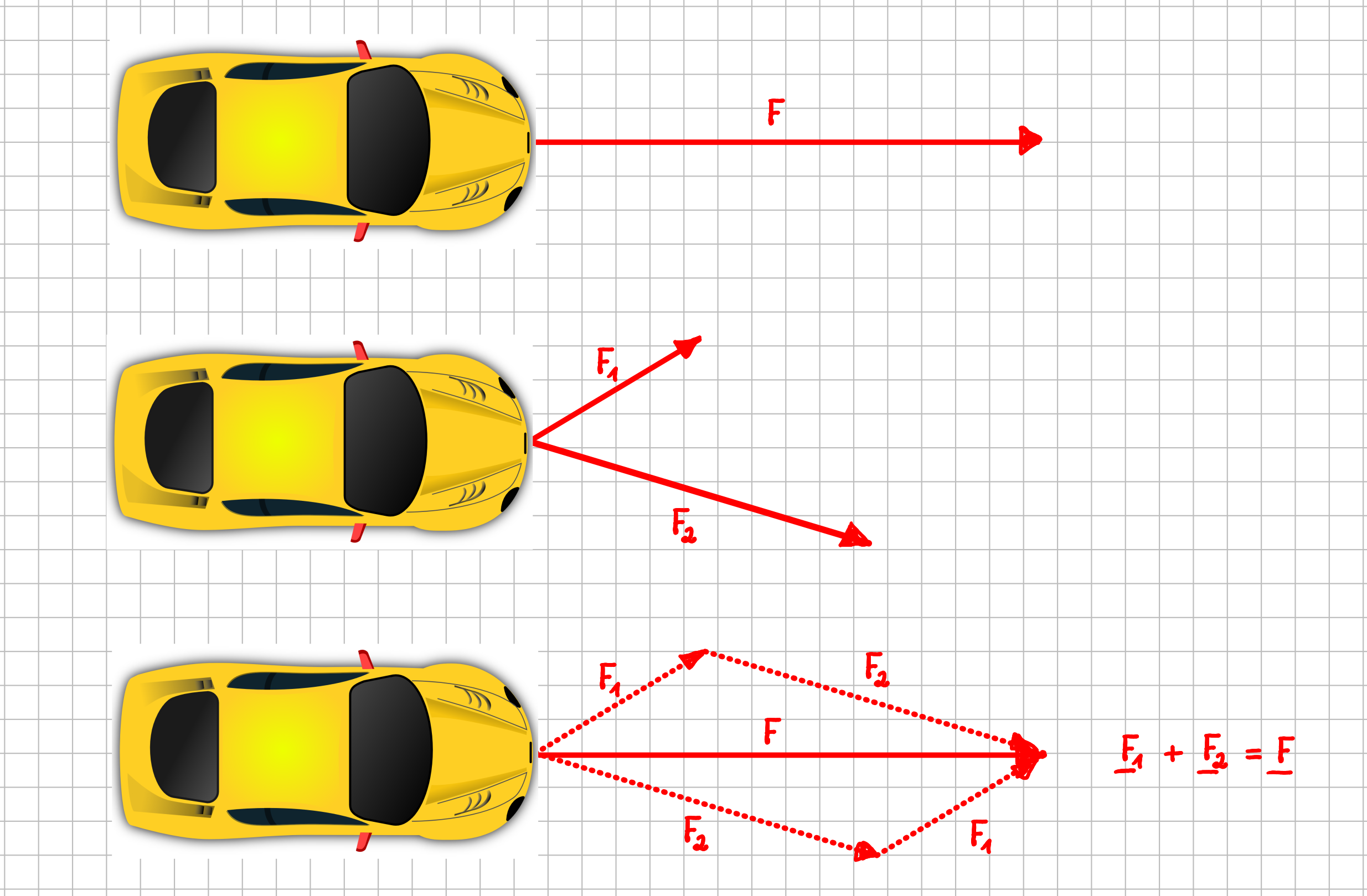
Anwenden der Vektoraddition beim Freischleppen eines Fahrzeugs
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2146/Anwenden_der_Vektoraddition_beim_Freischleppen.png
Wie sich aus den anschaulichen Beispielen aber auch aus den mathematischen Beziehungen sofort ergibt, ist die Addition zweier Vektoren vertauschbar. Es gilt also
$${\vec{a} + \vec{b} = \vec{b} + \vec{a}}$$
Für die Lateinfreaks: Das Kommutativgesetz gilt auch bei der Addition von Vektoren.
Zusammenfassung - Das Wichtigste in Kürze
Addition von Vektoren
Wenn zwei Vektoren \(\vec{a}\) und \(\vec{b}\) addiert werden, ist das Ergebnis wieder ein Vektor. Dies sei \(\vec{c}\) . Die Komponenten von \(\vec{c}\) ergeben sich, indem die Komponenten von \(\vec{a}\) und \(\vec{b}\) einzeln addiert werden.
$$\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \qquad\vec{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \quad \rightarrow \quad \vec{a}+\vec{b}=\begin{pmatrix} a_1+b_1 \\ a_2+b_2 \\ a_3+b_3 \end{pmatrix} =\vec{c}$$
Bei der Addition von Vektoren ist die Reihenfolge vertauschbar, d.h. es gilt das Kommutativgesetz.
$$\vec{a} + \vec{b} = \vec{b} + \vec{a}$$
Graphisch lässt sich die Addition als "Hintereinanderschaltung" der beiden Vektoren verstehen
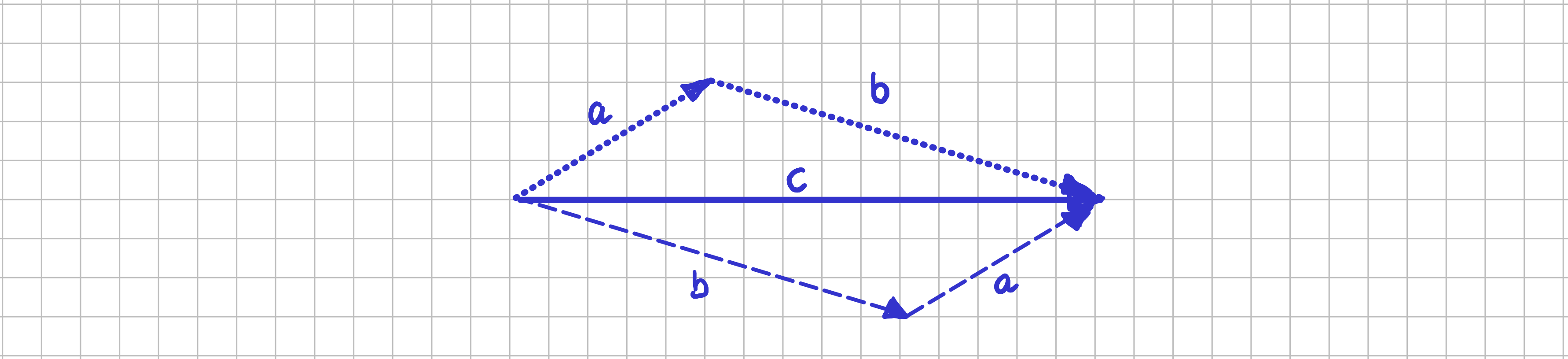
Addition von Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://writemd.rz.tuhh.de/uploads/a8e868b3e0e3a27307fed831c.png
 Addiere die Vektoren zeichnerisch und rechnerisch
Addiere die Vektoren zeichnerisch und rechnerisch