Vektorrechnung
Vektorrechnung
2. Was ist ein Vektor eigentlich?
2.3. Richtung und normierte Vektoren
Richtung und normierte Vektoren
Wenn du dich für die Richtung eines Vektors interessierst, dann kann es hilfreich sein, wenn du den Einheitsvektor für die durch den Vektor gegebene Richtung kennst. Wenn du diesen normierten Vektors hast, kannst du ihn durch Malnehmen mit einer Zahl beliebig lang machen.
Wenn du den zu einem gegebenen Vektor gehörenden Einheitsvektor bestimmst, dann nennt man diesen Vorgang Normieren.
Wenn ein Vektor normiert wird, dann bedeutet das, dass man ihn so umformt, dass er die Länge \( 1\) hat. Normierte Vektoren werden daher auch als Einsvektoren oder Einheitsvektoren bezeichnet. Bei den Vektoren
$$\vec{e}_x=\begin{pmatrix}1\\0\\0\end{pmatrix},\qquad\vec{e}_y=\begin{pmatrix}0\\1\\0\end{pmatrix},\qquad\vec{e}_z=\begin{pmatrix}0\\1\\0\end{pmatrix}$$
ist offensichtlich, dass es sich um Einheitsvektoren handelt.
Es ist aber möglich, jeden beliebigen Vektor auf die Länge \( 1\) zu bringen. Schauen wir uns das an einem Beispiel an.
Zahlenbeispiel
$$\vec{r}=\begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} \quad \rightarrow \quad \left| \vec{r} \right|=\sqrt{2^2+(-1)^2+3^2}=\sqrt{14} \\\rightarrow \quad \vec{\hat{r}}=\frac{1}{\left| \vec{r} \right|}\vec{r}=\frac{1}{\sqrt{14}}\begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}$$
Der Vektor \(\vec{r}\) hat die Länge \(\sqrt{14}\). Teilen wir den Vektor durch diese Länge, hat er wie gewünscht die Länge \(1\). Normierte Vektoren werden dabei oft auch mit einem "Dach" gekennzeichnet: \(\vec{\hat{r}}\).
Die allgemeine Rechnenvorschrift zur Normierung eines Vektors \(\vec{r}\) lautet also:
$${\vec{\hat{r}}=\frac{1}{\left| \vec{r} \right|}\vec{r}}$$
Ein normierter Vektor hat die Länge \(1\) und zeigt in die Richtung des ursprünglichen Vektors.
Ein normierter Vektor ist immer einheitenlos, da durch den Betrag des Vektors geteilt wird. Und da der Betrag dieselbe Einheit hat, wie die einzelnen Komponenten, kürzen sich die Einheiten weg.
In der Mechanik kommen normierte Vektoren an verschiedenen Stellen zum Einsatz. Wird eine Struktur z.B. von einem Seil abgestützt, so kann die Richtung des Seils, nennen wir sie \(\vec{r}_{\mathrm{Seil}}\) aus der Geometrie berechnet werden. Wird dieser Vektor normiert, liegt ein Vektor mit Länge \(1\) in Richtung der Seilkraft vor: \(\vec{\hat{r}}_{\mathrm{Seil}}\) Die Seilkraft \(\vec{S}\) mit dem Betrag \(S\) lässt sich dann angeben als \(\vec{S}=S \cdot\vec{\hat{r}}_{\mathrm{Seil}}\).
Beispiel
Der Eckpfosten eines Gartenzaunes ist bei Punkt \(A\) fest im Boden verankert. Zusätzlich wird er durch ein Seil, dass die Punkte \(B\) und \(C\) verbindet, gehalten. Der Pfosten wird in Punkt \(B\) durch die Kräfte \(\left| \vec{F}_1 \right| = F\) und \(\left| \vec{F}_2 \right| = F\) belastet. Die Kraft im Seil ist \(\vec{S}\) mit \(\left| \vec{S} \right| = S\).
Die Lage der Punkte \(B\) und \(C\) ist gegeben durch die Vektoren
$$\vec{r}_{AB}=\begin{pmatrix}
0 \\ 0 \\ 2a \end{pmatrix} \quad \mathrm{und} \quad \vec{r}_{AC}=\begin{pmatrix}
-a \\ -a \\ 0 \end{pmatrix}$$
Gesucht ist der Vektor der Seilkraft \(\vec{S}\) .
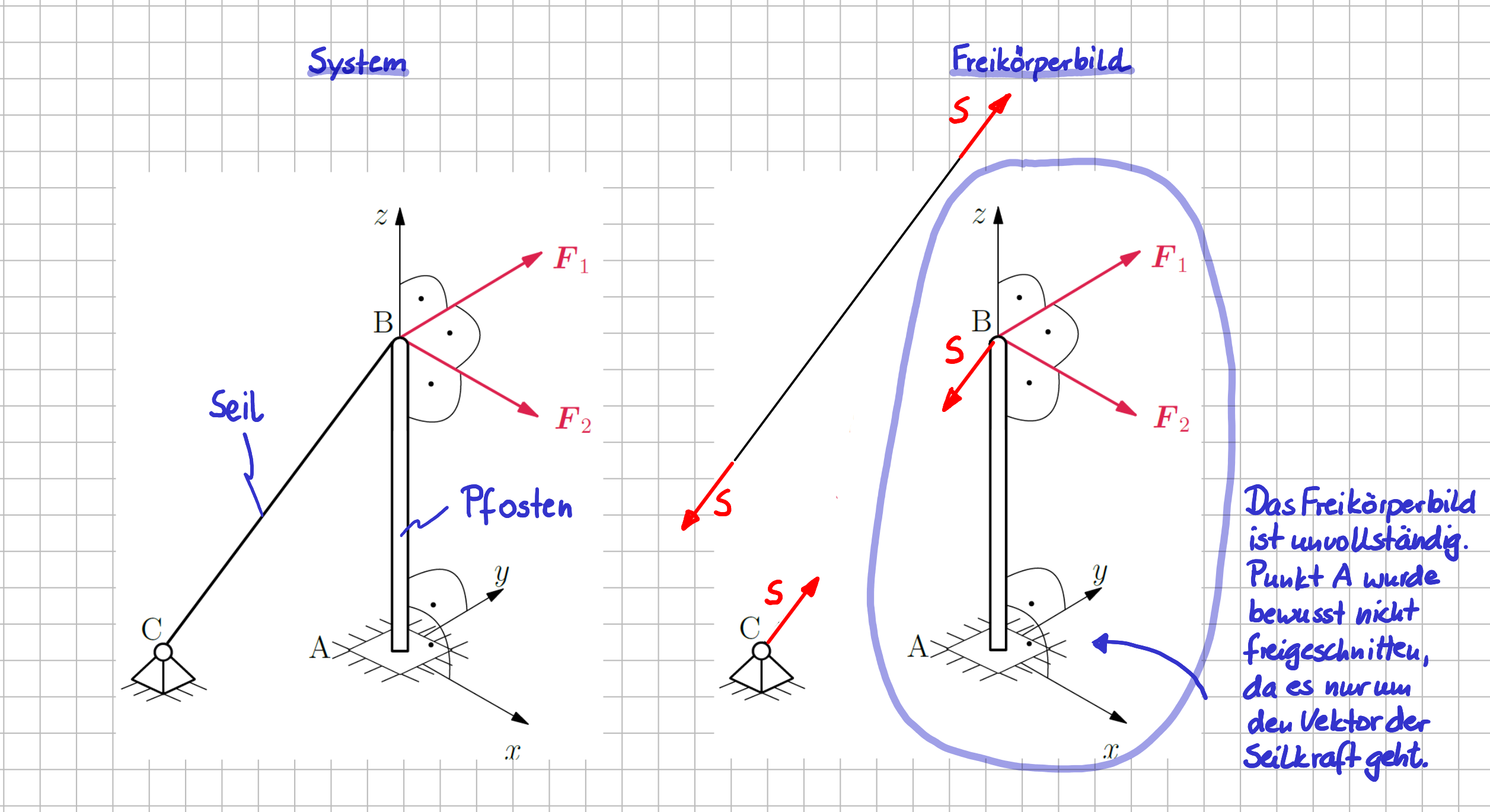
Anwendungsbeispiel: Abstützung eines Pfostens mit einem Seil
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2145/Aanwendungsbeispiel_Abstuetzung_eines_Pfostens.png
$$\vec{S}=S\cdot \vec{\hat{r}}_{BC},$$
da der Betrag \(S\) der Seilkraft ja laut Aufgabenstellung bekannt ist.
Es muss also lediglich der normierte Vektor von \(B\) nach \(C\) bestimmt werden. Es gilt
$$\vec{r}_{BC}=\vec{r}_{AC}-\vec{r}_{AB}=\begin{pmatrix}
-a \\ -a \\ 0 \end{pmatrix}-\begin{pmatrix} 0 \\ 0 \\ 2a
\end{pmatrix}=\begin{pmatrix} -a \\ -a \\ -2a \end{pmatrix}.$$
Die Länge dieses Vektors ergibt sich zu
$$\left| \vec{r}_{BC}\right|=\sqrt{(-a)^2+(-a)^2+(-2a)^2}=\sqrt{6}a.$$
Damit gilt für den normierten Vektor in Richtung von \(B\) nach \(C\)
$$\vec{\hat{r}}_{BC}=\frac{1}{\sqrt{6}a}\cdot \begin{pmatrix} -a \\ -a \\ -2a \end{pmatrix}=\frac{1}{\sqrt{6}}\cdot \begin{pmatrix} -1 \\ -1 \\ -2 \end{pmatrix}.$$
Und für den Vektor \(\vec{S}\) der Seilkraft folgt unter Berücksichtigung der oben bereits aufgestellten Beziehung
$$\vec{S}=S\cdot \vec{\hat{r}}_{BC} = \frac{S}{\sqrt{6}}\begin{pmatrix} -1 \\ -1 \\ -2 \end{pmatrix}.$$
Es ist immer hilfreich, einen Plausibilitätscheck durchzuführen. Die Komponenten des Ergebnisvektors haben die Einheit einer Kraft: Check. Alle Komponenten des Ergebnisvektors sind negativ. Da, wie im Freikörperbild ersichtlich ist, alle Komponenten - in Bezug auf das zugrundegelegte Koordinatensystem - in negative Achsrichtung zeigen, ist das Ergebnis auch in diesem Punkt plausibel: Check.
Das beschriebene Vorgehen lässt sich auch für Stabkräfte in Fachwerken anwenden. Dieser Fall wird in einem der Arbeitsblätter behandelt.
Zusammenfassung - Das Wichtigste in Kürze
Normierter Vektor
$$\quad\vec{\hat{r}}=\dfrac{1}{\left| \vec{r} \right|}\vec{r}$$
Ein normierter Vektor hat die Länge 1 und zeigt in die Richtung des ursprünglichen Vektors. Er wird auch Einsvektor oder Einheitsvektor genannt.
Ein normierter Vektor ist immer einheitenlos, da durch den Betrag des Vektors geteilt wird. Und da der Betrag dieselbe Einheit hat, wie die einzelnen Komponenten, kürzen sich die Einheiten weg.
Ist der Einsvektor in eine bestimmte Richtung bekannt, kann ein beliebiger Vektor, der in diese Richtung zeigt, leicht angegeben werden:
$$\vec{F}=F\cdot \vec{\hat{r}}_{AB}$$
Vektor mit Betrag \(F\) in Richtung der Strecke von Punkt \(A\) nach Punkt \(B\).

