Vektorrechnung
Vektorrechnung
2. Was ist ein Vektor eigentlich?
2.1. Definition und Darstellung
Definition und Darstellung eines Vektors
Im realen Leben gibt es viele Größen – z.B. Geschwindigkeit, Beschleunigung, Kraft, Moment, Impuls, Drall – die nur vollständig charakterisiert werden können, wenn man den Betrag und die Richtung, in die die jeweilige Größe wirkt, kennt. Man nennt diese Größen daher auch gerichtete Größen. Und um genau solche Größen mathematisch beschreiben zu können, werden Vektoren verwendet. Vektoren haben eine Länge, allgemeiner sagt man auch einen Betrag, und sie geben die Richtung der Größe an, die sie beschreiben. Und es spielt eine Rolle, wo die entsprechende Größe wirkt. Informationen über die Lage oder den Angriffspunkt der Größe braucht es also auch noch.
Für die graphische Darstellung eines Vektors wird ein Pfeil verwendet. Das ist im Straßenverkehr nicht anders. Der Pfeil gibt die Richtung an.

Pfeil zur Angabe der Richtung im Straßenverkehr
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Pfeil_zur_Angabe_der_Richtung_im_Stra%C3%9Fenverkehr.png?time
In der Mathematik steht neben dem Pfeil der Betrag/die Länge des Vektors. Das kann eine Zahl oder eine Variable sein. Im Fall einer Kiste mit einer Masse von \(m_1=10\mathrm{kg}\) , also einer Gewichtskraft von etwa \( G_1 = m_1 \cdot g= 100\mathrm{N} \) , sieht das dann so aus. Eine doppelt so schwere Kiste ist in der Abbildung ebenfalls dargestellt.
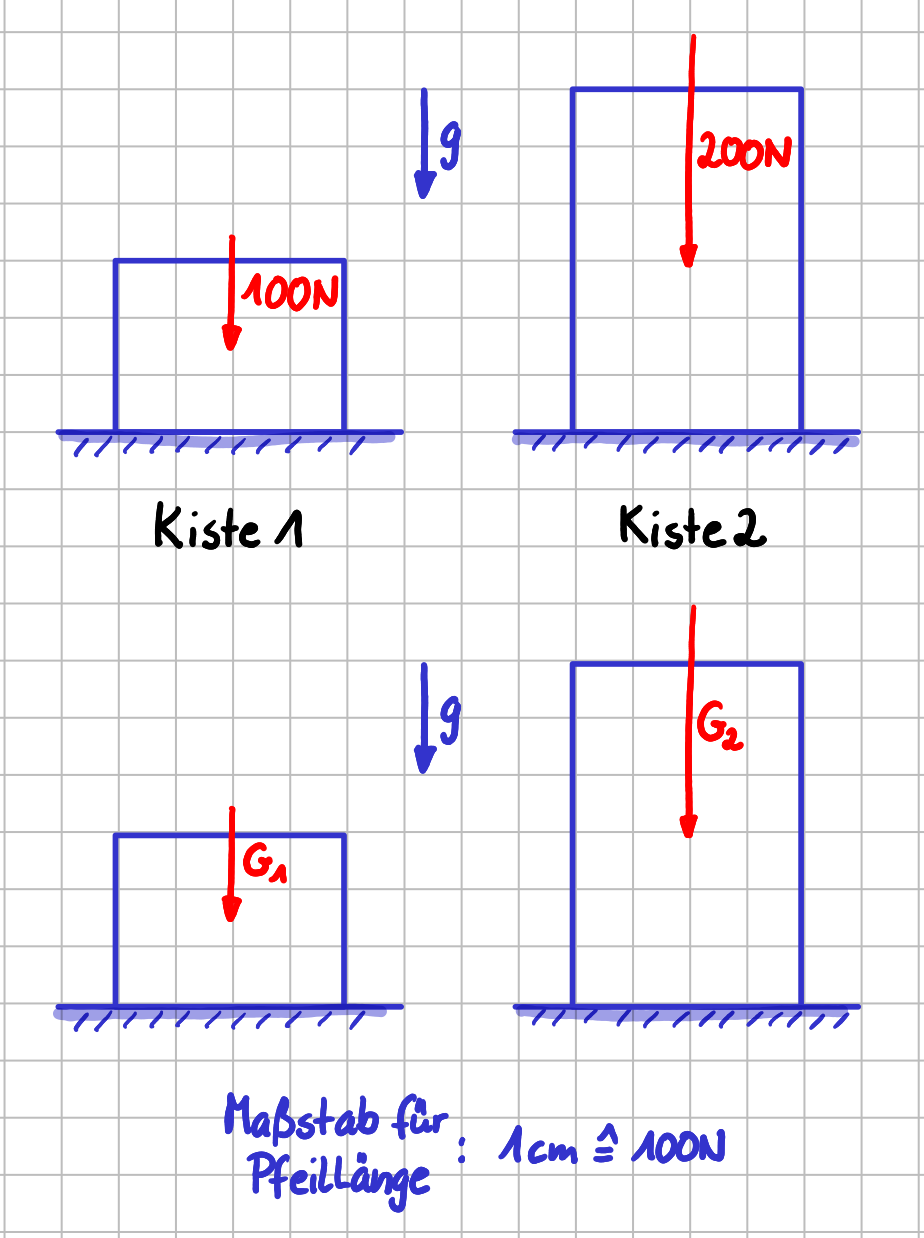
Verschiedene Darstellungsvarianten für den Betrag eines Vektors: maßstäbliche Pfeillänge
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Verschiedene_Darstellungsvarianten_Vektor_01.png
Werden Vektoren maßstäblich gezeichnet, entspricht die Länge des Pfeils dem Betrag des Vektors. Ein doppelt so langer Pfeil bedeutet dann also, dass die Gewichtskraft des zweiten Objektes doppelt so groß ist. In dieser Darstellungsvariante enthält der Pfeil also die Richtungs – und die Betragsinformation, so lange der Maßstab bekannt ist. Die Angabe des Betrags als "Zahl daneben" ist dann theoretisch doppeltgemoppelt, dient aber in jedem Fall der Übersicht.
Oft werden aber alle Pfeile gleich lang dargestellt.
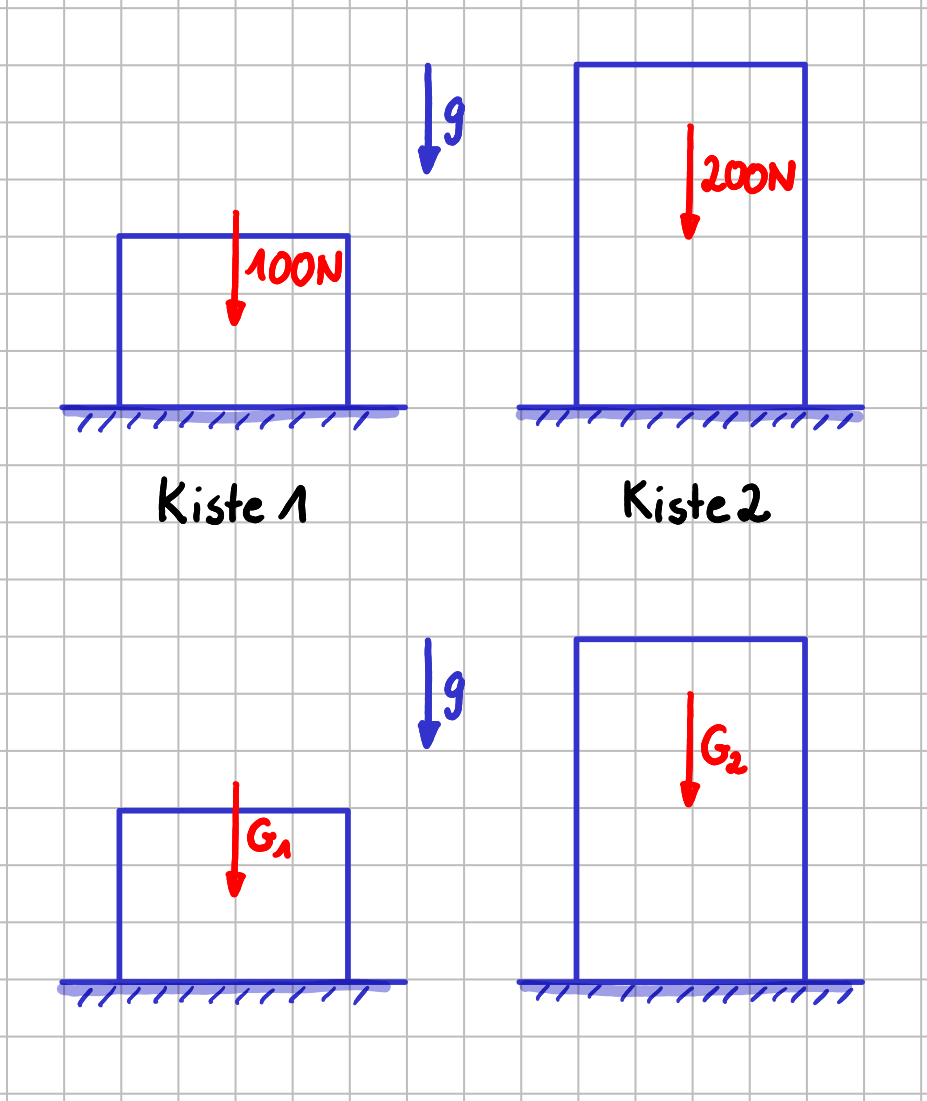
Verschiedene Darstellungsvarianten für den Betrag eines Vektors: einheitliche Pfeillänge
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Verschiedene_Darstellungsvarianten_Vektor_02.png
In diesem Fall wird durch die Richtung des Pfeils die Richtung der physikalischen Größe angegeben. Die Information zum Betrag ergibt sich einzig und allein aus der Zahl oder der Variablen, die neben dem Pfeil steht.
An dieser Stelle vielleicht ein paar Worte zum Thema Variablen: Werden wie in der Mechanik physikalische Zusammenhänge betrachtet, ist es hilfreich und sinnvoll, die beschreibenden Gleichungen erst einmal mit Variablen aufzustellen. Dies setzt voraus, dass z.B. für die Beträge von Vektoren, aber eben auch für Abstände, zunächst Variablen verwendet werden und nicht gleich Zahlenwerte. Die Zahlenwerte werden erst ganz am Ende eingesetzt. Was ist der Vorteil dieser Vorgehensweise? Der größte Vorteil ist, dass man allgemeingültige Gleichungen für ein System erhält. Man kann also für ein und dasselbe System sehr einfach verschiedene Varianten durchrechnen. Nehmen wir einmal das Beispiel einer Brücke. Aus Ingenieurssicht interessiert z.B. die Beanspruchung der Brückenpfeiler, wenn nicht so viel Verkehr herrscht. Genauso interessant ist aber auch die Belastung zur Rush Hour, wenn fünf Mal so viel Verkehr fließt, also deutlich mehr Gewicht auf den Pfeilern lastet. Stehen die Gleichungen in Form von Variablen zur Verfügung, können unterschiedliche Zahlenwerte für die Belastung einfach eingesetzt und die daraus resultierenden Beanspruchungen der Pfeiler für unterschiedliche Lastszenarien ausgerechnet werden. Genauso einfach könnte überprüft werden, wie es sich auf die Beanspruchung der Pfeiler auswirkt, wenn die Länge der Brücke z.B. um 20% erhöht wird.
Exkurs zum Thema Gleichgewichtsbedingungen
In der Mechanik werden typischer Weise vorzeichenbehaftete Beträge neben dem Vektorpfeil angegeben. Wenn du jetzt denkst, “Moment mal, ein Betrag ist per Definition doch positiv!”, dann hast du natürlich recht. So, wie die Vektoren in der Mechanik zum Beispiel in Freikörperbildern für Kräfte verwendet werden, erhält man durch Auswerten der Gleichgewichtbedingungen aber einen vorzeichenbehafteten Wert. Schauen wir uns das für das dargestellte System mal für die Kraft \(𝐴_𝐻\) genauer an.
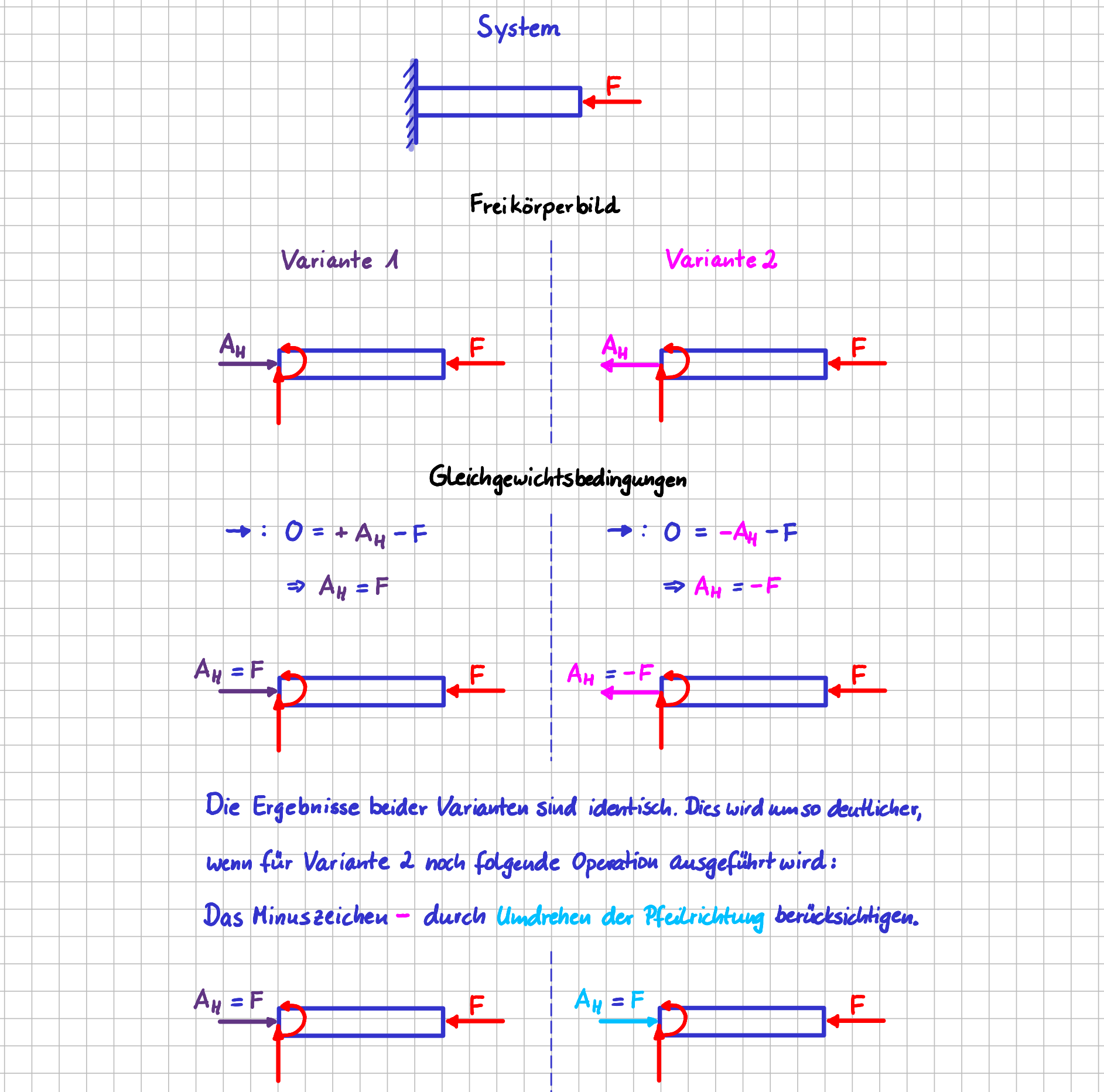
Vorzeichenbehaftete Beträge am Beispiel eines fest eingespannten Balkens
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Vorzeichen_behaftete_Betraege.png
Freikörperbild-Variante 1:
Wird die Kraft beim Freischneiden mit Pfeilspitze "nach rechts" eingezeichnet, ergibt sich aus dem Kräftegleichgewicht in horizontaler Richtung \(A_H=F\).
Freikörperbild-Variante 2:
Wird die Kraft \(A_H\) beim Freischneiden mit Pfeilspitze "nach links" eingezeichnet, ergibt sich aus dem Kräftegleichgewicht in horizontaler Richtung \(A_H=(-F)\).
\(A_H\) hat in beiden Fällen den Betrag \(F\). Und dieser Betrag ist positiv. Das Minuszeichen in der zweiten Variante allerdings zeigt an, dass die Kraft \(A_H\) nicht in die angenommene Pfeilrichtung im Freikörperbild zeigt, sondern in die entgegengesetzte Richtung. Im Vorzeichen ist also noch zusätzlich zum Betrag die Richtungsinformation enthalten. Ergebnisse aus den Gleichgewichtsbedingungen müssen also immer im Zusammenhang mit den gewählten Pfeilrichtungen für die Vektoren im Freikörperbild gesehen werden. Der Ausdruck “Neben dem Vektorpfeil steht der vorzeichenbehaftete Betrag.” ist also die Langform für “Neben dem Vektorpfeil steht der Betrag. Das Vorzeichen davor gibt zusätzlich die Richtungsinformation an: ‘+’ bedeutet in Richtung des eingezeichneten Pfeils, ‘-’ bedeutet entgegen der Richtung des eingezeichneten Pfeils”.
Für Variante 1 und Variante 2 ergibt sich also das identische Ergebnis. Dies war selbstverständlich auch zu erwarten, da es der Physik egal ist, welchen Ansatz wir als diejenigen, die ein Modell erstellen, zur Beschreibung wählen. Das physikalische Prinzip “Statisches System im Gleichgewicht” gilt ja unabhängig von irgendeinem konkreten Beschreibungsansatz.
Für die mathematische Darstellung von Vektoren werden verschiedene Schreibweisen verwendet. Je nach Quelle werden Vektoren fett, mit Unterstrich oder mit einem Pfeil darüber dargestellt. Diese drei Darstellungen beschreiben also ein und denselben Vektor:
$$\mathbf{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\hspace{3cm} \underline{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\hspace{3cm} \vec{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}$$
Auch bei der Wahl der Klammerart gibt es verschiedene Schreibweisen: es werden sowohl runde als auch eckige Klammern verwendet. Um Vektoren auch in einer Zeile schreiben zu können, wird das sogenannte transponiert-Zeichen verwendet.
$$
\underline{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} \qquad \leftrightarrow \qquad \underline{r}=[1\quad 0\quad -1]^T
$$
Zwei Vektoren sind immer dann identisch, wenn sie dieselbe Richtung und denselben Betrag haben, also gleich lang sind. Alle in der folgenden Abbildung gezeigten Vektoren sind daher identisch: $$\vec{a}\ =\ \vec{b}\ =\ \vec{c}\ =\ \vec{d}$$
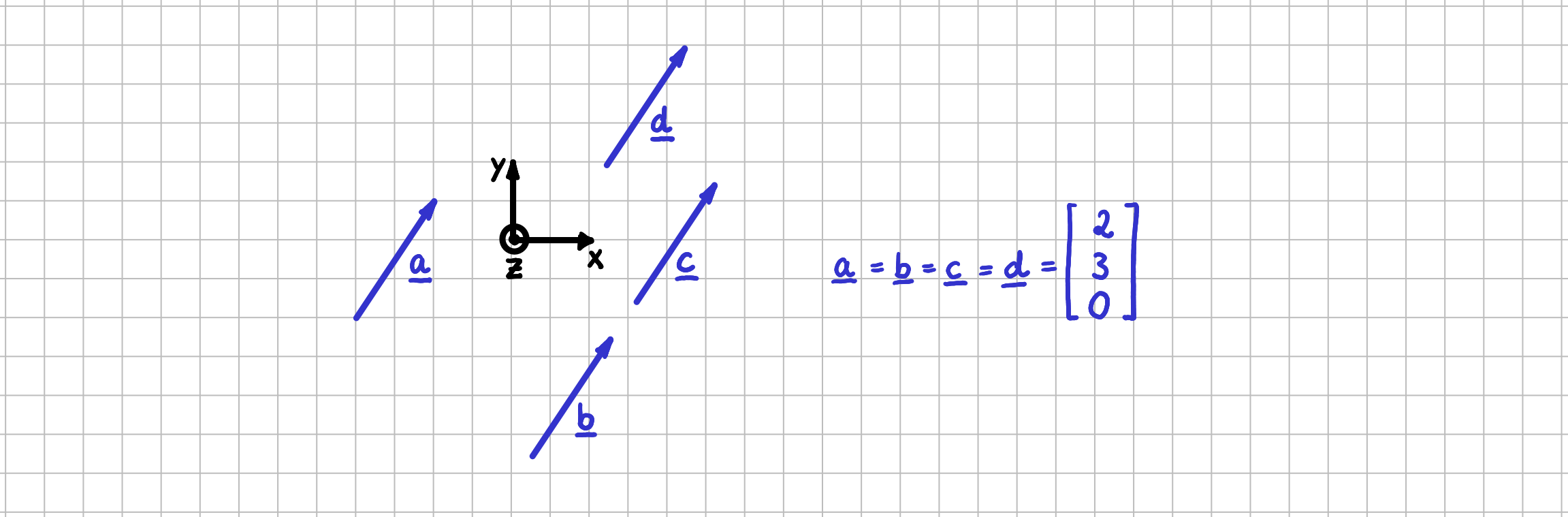
Identische Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Identische_Vektoren.png
Zusammenfassung - Das Wichtigste in Kürze
Darstellungsformen für Vektoren
Es gibt verschiedene Darstellungsformen für Vektoren. Alle folgenden mathematischen Darstellungen sind identisch:
$$\mathbf{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\qquad \underline{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}\qquad \vec{r}=\begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} \qquad\underline{r}=[1\quad 0\quad -1]^T$$
Für die graphische Darstellung wird ein Pfeil verwendet. Neben dem Pfeil steht der vorzeichenbehaftete Betrag.
Das Vorzeichen vor dem Betrag gibt zusätzlich die Richtungsinformation an:
’ + ’ bedeutet in Richtung des eingezeichneten Pfeils,
’ - ’ bedeutet entgegen der Richtung des eingezeichneten Pfeils.
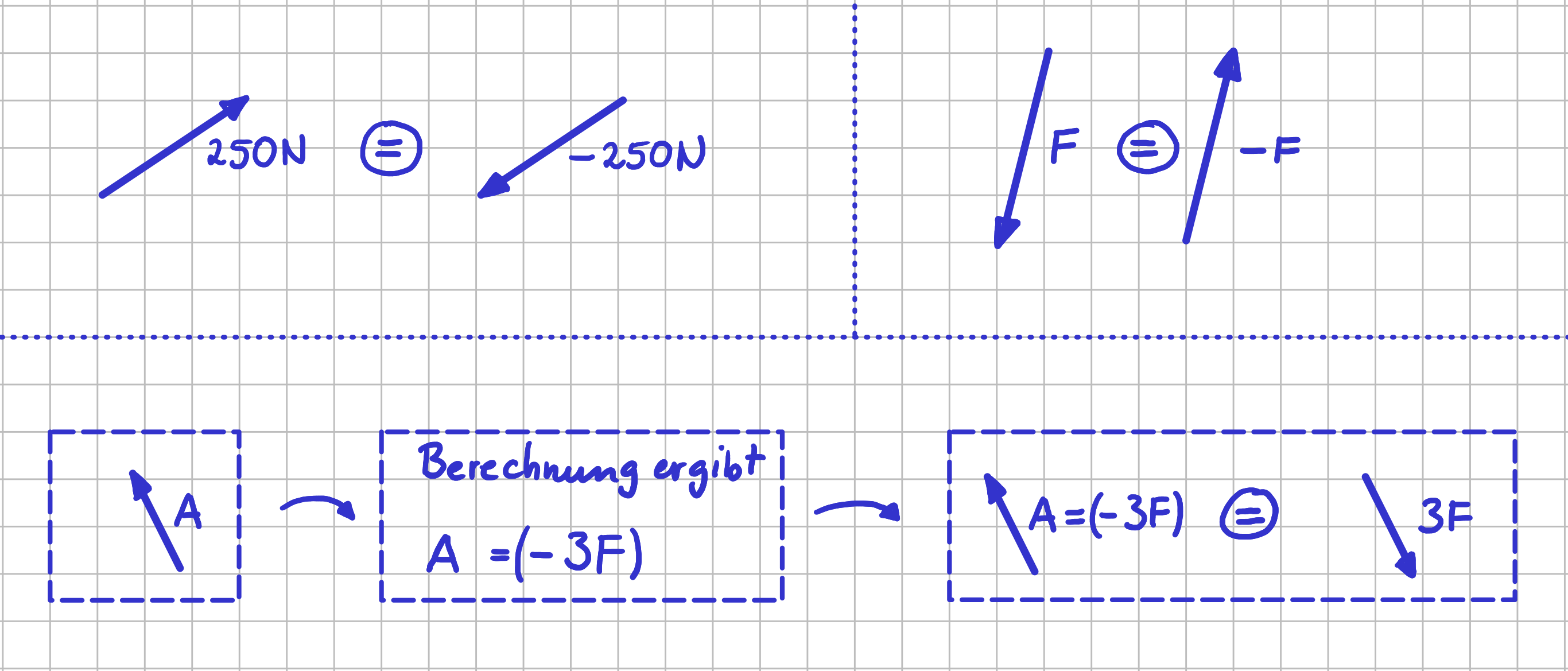
Vorzeichenbehaftete Beträge
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2143/Vorzeichen_behaftete_Betraege_02.png