Vektorrechnung
Vektorrechnung
2. Was ist ein Vektor eigentlich?
Was ist ein Vektor eigentlich?
Wenn du das Wort “Vektor” hörst, reagierst du automatisch in irgendeiner Form. Du kannst gar nicht anders. Diese Reaktion wird von Mensch zu Mensch unterschiedlich sein, aber tendenziell eher positiv – Cool, Vektoren! – oder eher negativ – Oje, schon wieder Vektoren! – gefärbt sein.
Egal, wie deine ganz individuelle Reaktion ausfällt, erlaub dir gerade in dem Fall, in dem du tendenziell negativ reagierst, das Thema “Vektoren” noch einmal ganz neu kennenzulernen. Du wirst in diesem Abschnitt sehen, warum es sich lohnt.
Stell dir vor, du bist irgendwo in einer Stadt, in der du dich nicht so gut auskennst. Du bist auf der Suche nach einem Bäcker und fragst jemanden auf der Straße nach dem Weg: “Wo ist denn hier der nächste Bäcker?”. Wenn du als Antwort bekommst, “Der ist etwa 500m von hier.” weißt du schon mal, dass du nur etwa 5 Minuten brauchen wirst, um dorthin zu kommen. Du hast aber noch keine Idee, in welche Richtung du gehen musst. Die reine Angabe der Streckenlänge hilft dir also nur bedingt weiter. Du kommst erst zum Ziel, wenn du auch noch Informationen über die Richtung bekommst, in die du gehen musst. Vermutlich wird die Person, die du gefragt hast, dir mit einer Hand noch die Richtung zeigen. Damit bekommst du dann also auch noch die benötigte Richtungsinformation. Und ohne, dass du es gemerkt hast, hast du auch schon mit Vektoren zu tun. Vektoren kombinieren nämlich genau zwei Angaben: die Information über eine Länge (oder allgemeiner gesagt über einen Betrag) und die Information über die Richtung. Und wie du gerade gemerkt hast, ist es für eine Kommunikation in oder über die reale Welt ungeheuer wichtig, beide Informationen zu haben und das am besten noch zur selben Zeit.
Du wirst sicherlich zustimmen, dass es total hilfreich ist, wenn Menschen ihre Hände oder Arme verwenden, um die Richtungen eines Weges zu zeigen. In der Mathematik wird hierfür ein Pfeil verwendet. So wird es ja zum Beispiel auch im Straßenverkehr gemacht. Der Pfeil gibt die Richtung an. Und der Zahlenwert, der daneben geschrieben wird, ist die Länge, die in die angegebene Richtung zurückgelegt werden muss. Beide Informationen zusammen bezeichnet man als Vektor. Im Beispiel sähe die Situation also so aus:
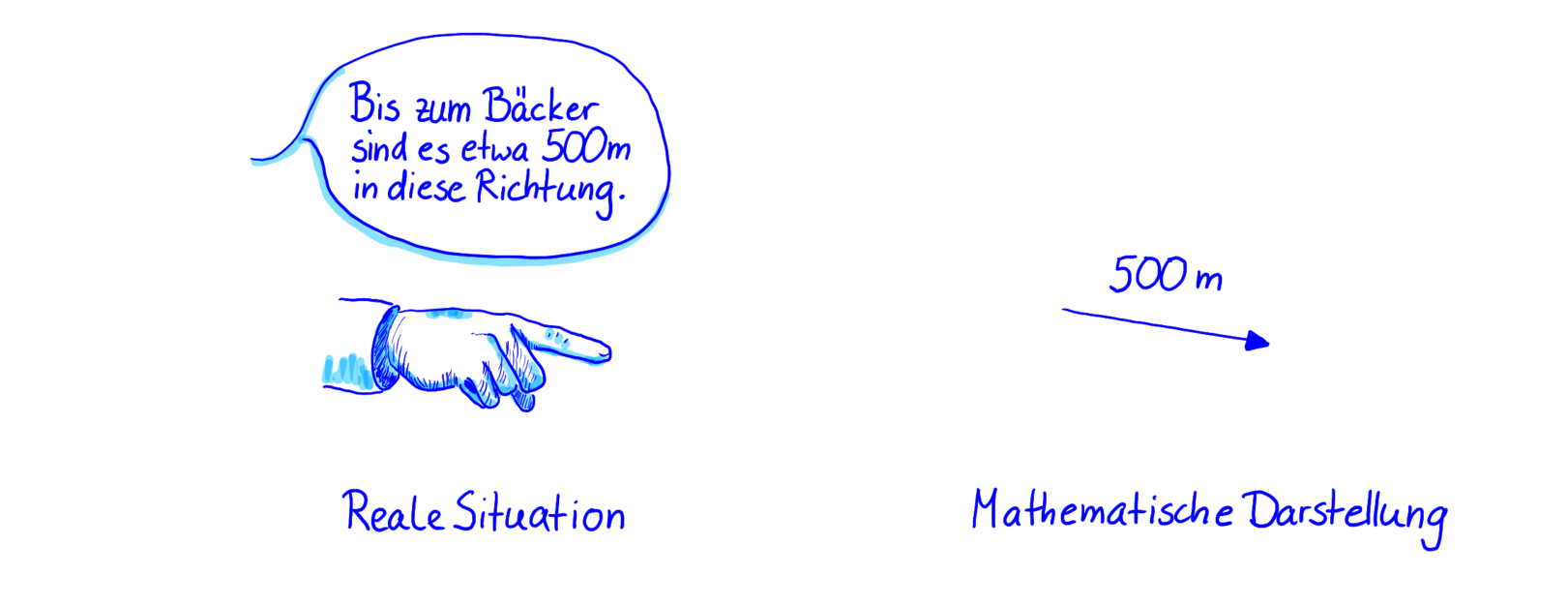
Angabe einer Weginformation mit Richtung und Betrag
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2142/Angabe_einer_Weginformation.png
Im realen Leben, und damit in der Physik, die versucht, Vorgänge im realen Leben zu beschreiben, gibt es ganz viele Größen, die die Angabe eines Betrags und einer Richtung brauchen. Sonst wären sie schlicht und einfach sinnlos und es würde zum Teil richtig gefährlich. Du findest also überall Vektoren. Wenn du auf dem Fahrrad unterwegs bist und einem Kind, das hinter einem Auto hervorspringt, ausweichen willst, dann beschleunigst oder verzögerst du in eine bestimmte Richtung. Tada, ein Vektor. Wenn du auf Skiern oder einem Mountainbike einen Hang runterfährst und in eine Linkskurve gehst, dann wirken da hoffentlich Kräfte in der richtigen Größe und in der richtigen Richtung; sonst liegst du nämlich schnell auf der Nase. Tada, schon wieder ein Vektor. Und du möchtest doch auch, dass die Ingenieurinnen und Ingenieure, die das Haus berechnet haben, in dem du wohnst, alle auftretenden Kräfte (z.B. Eigengewicht, Windlast, Schneelast) ordnungsgemäß nach Größe und Richtung berücksichtigt haben, oder? Tada, schon wieder Vektoren. Und auch die Möbel, die du nutzt, die Brücken, die du passierst, die Maschinen und Verkehrsmittel, die du nutzt, – Toaster, Föhn, Rasenmäher,Fahrrad, Roller, Bus, Auto, Flugzeug – sind hoffentlich alle so ausgelegt, dass sie allen auftretenden Belastungen – egal ob statisch oder dynamisch – standhalten. Du siehst also: Kräfte und Momente, Beschleunigungen und Geschwindigkeiten sind ganz wesentliche Vektoren und begegnen dir Tag aus Tag ein.
Es lohnt sich also wirklich, sich mit dem Konzept “Vektoren” zu beschäftigen, ja mehr noch: anzufreunden. Vektoren sind einfach unglaublich nützlich … und einfach anzuwenden, wenn man das Prinzip verstanden hat. Und genau beim (weiteren) Verstehen soll dir dieses Kapitel helfen.
In den weiteren Abschnitten findest du allgemeine Informationen zur Definition und Darstellung eines Vektors. Mit den drei Kenngrößen eines Vektors, seinem Betrag, seiner Richtung und seinem Angriffspunkt kannst du dich dann noch genauer beschäftigen.