Trigonometrie
Trigonometrie
2. Gradmaß und Bogenmaß
Gradmaß und Bogenmaß
Dass Winkel in Grad also "°" angegeben werden, hast du in der Schule gelernt. Wenn du dich einmal komplett um deine Hochachse drehst, hast du dich um 360° gedreht. 360° sind also 'einmal rum'. Alle anderen Winkel lassen sich als Anteile von 360° angeben. Auf deinem Geodreieck zum Beispiel hat die eine Ecke 90° (das ist ein rechter Winkel) und die anderen beiden Ecken haben 45°. Die Einteilung auf dem Geodreieck ist typischer Weise in 1°-Schritten.
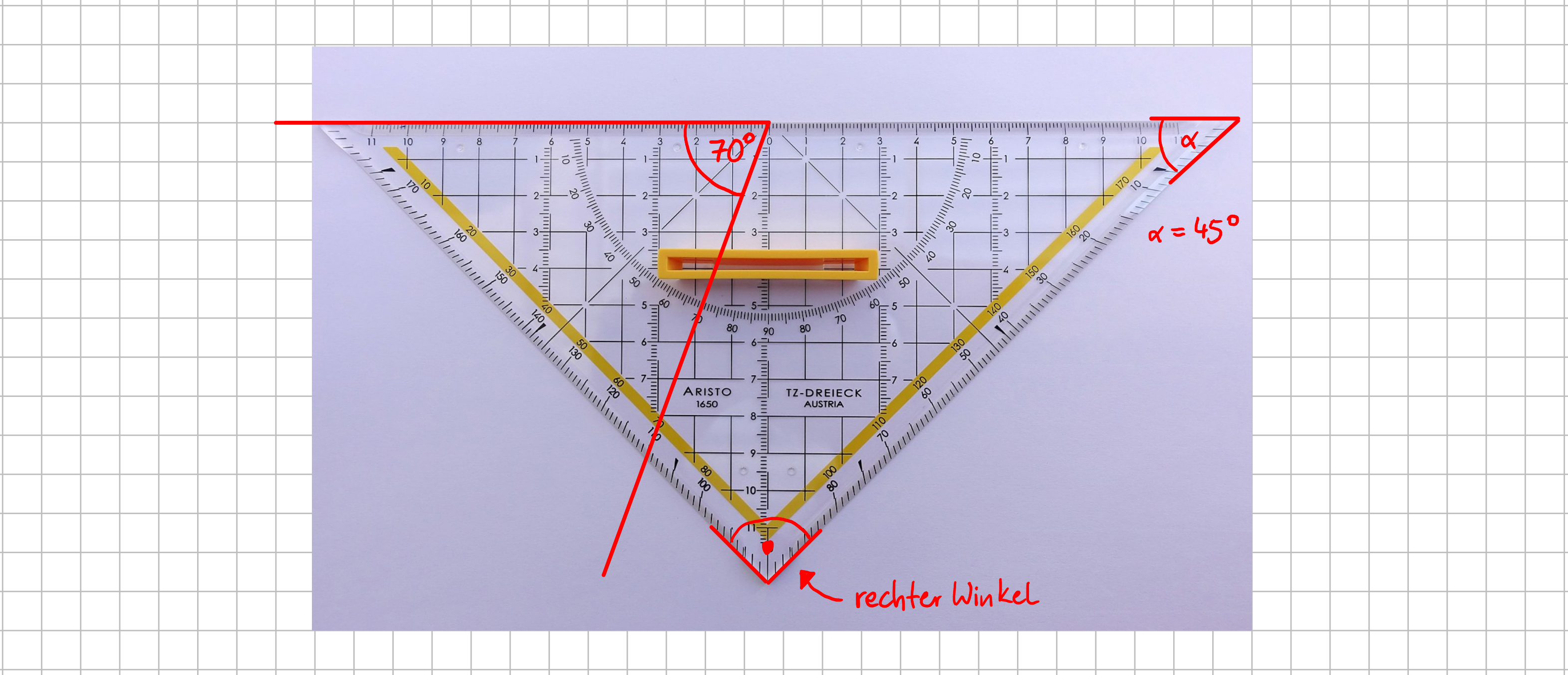
Typische Winkel und messen allgemeiner Winkel mit dem Geodreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg auf Basis von Kmtextor
CC BY-SA 4.0
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2140/Typische_Winkel_beim_Geodreieck.png
https://commons.wikimedia.org/w/index.php?curid=74388047
Jetzt kann man Winkel eben nicht nur in ° angeben, sondern auch über das Bogenstück, also die zum Winkel gehörende Strecke auf dem Kreis. In der folgenden Zeichnung ist ein Kreis mit dem Radius \( r \) dargestellt. Außerdem ist der Winkel \( \alpha \) eingezeichnet. Wenn der Radius \( r \) bekannt ist, kann man den Winkel statt über \( \alpha \) genauso gut über die Strecke \( b \) angeben.
Stell dir vor, du hast das Ende eines Seils irgendwo befestigt und hältst das andere Ende in der Hand am ausgestreckten Arm fest. Das Seil und dein ausgestreckter Arm sind zusammen so lang, dass zwischen dem Befestigungspunkt des Seils und deiner Körpermitte \(2\mathrm{m}\) liegen. Wenn du jetzt losläufst, musst du auf einem Kreis laufen. Und wenn du etwas mehr als \(1\mathrm{m}\) zurücklegst, hat das Seil einen Winkel von 30° überstrichen. “Wieso gerade \(1\mathrm{m}\)?”, fragst du? Lass uns doch einfach mal schauen, wie der Zusammenhang zwischen dem Winkel in ° und der Strecke \( b \) ist. (In der Zwischenzeit kannst du ja gerade mal den Versuch machen und nachmessen, ob \(1\mathrm{m}\) korrekt sind.)
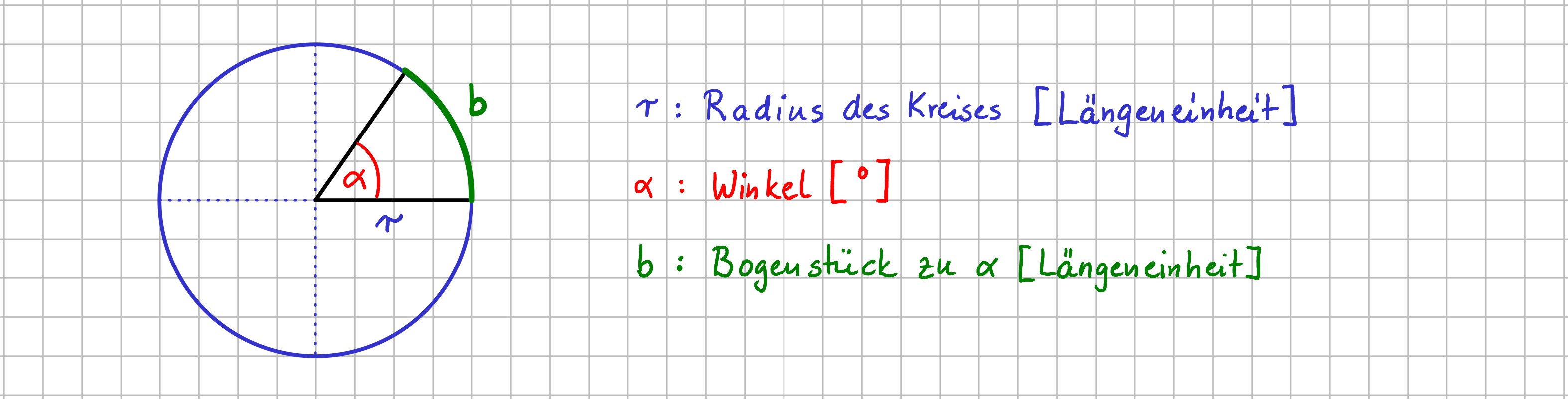
Grundgrößen, die bei der Umrechnung zwischen Winkeln in der Einheit Grad und rad benötigt werden
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2140/Grundgroessen_Umrechnung_Winkel_grad_rad.png
“Einmal rum” sind 360°. Das ist klar. Der Umfang eines Kreises, also die Strecke, wenn man einmal rum läuft, ist \( U = 2 \pi \cdot r \) lang. Das ist hoffentlich auch klar.
Wenn wir jetzt die beiden verschiedenen Arten von “einmal rum” ("einmal rum in ° " und “einmal rum als Bogenstück”) ins Verhältnis setzen, dann muss zwischen dem Winkel \( \alpha \) und der Strecke \( b \) dasselbe Verhältnis vorliegen, da "ein Stück rum in ° " gleich “ein Stück rum als Bogen” ist:
$$\frac{360°}{2\pi \cdot r} = \frac{\alpha}{b} \quad \rightarrow \quad \frac{180°}{\pi \cdot r} = \frac{\alpha}{b}$$
Wenn du diese Gleichung jetzt noch umstellst, um das Verhältnis aus \( b \) und \( r \) zu bekommen, dann steht da
$$\frac{b}{r}=\frac{\pi}{180°} \cdot \alpha$$
Das Verhältnis von Bogenstück zu Radius, also \( \frac{b}{r} \) wird als Bogenmaß des Winkels bezeichnet. Man schreibt dafür auch \( \mathrm{arc} \alpha \) . Es wird in der Einheit rad angegeben, auch wenn es formal einheitenlos ist. So kann man aber kennzeichnen, dass es sich bei der angegebenen Zahl um eine Winkelangabe handelt.
Ein Winkel von 1 rad liegt also genau dann vor, wenn der Radius \( r \) den Wert ‘1 Längeneinheit’ hat, du also auf einem Kreis mit einem Radius von \( r = 1\mathrm{m}\) auch genau \(1\mathrm{m}\) auf dem Umfang zurücklegst.
Für die Umrechnung gilt also
$${\mathrm{arc}\ \alpha =\frac{b}{r} = \frac{\pi}{180°} \cdot \alpha}$$
oder in Worten
$${\mathrm{Winkel\ in\ rad\ }= \ \frac{\pi}{180°} \ \cdot \mathrm{Winkel\ in\ Grad}}$$
Schauen wir uns jetzt nochmal das Beispiel mit dem Seil an. Du erinnerst dich: Du hast ein Seil in der Hand, dessen eines Ende festgemacht ist. Der Abstand zwischen diesem Punkt und deiner Körpermitte ist so, dass du dich auf einem Kreis mit dem Radius von \(2\mathrm{m}\) bewegst. Es soll ein Winkel von 30° überstrichen werden. Ich habe behauptet, dass du dafür “etwas mehr als \(1\mathrm{m}\)” auf der Kreisbahn gehen musst. Setzen wir also in die Formel ein:
$$\mathrm{Winkel\ in\ rad}=\frac{\pi}{180°}\cdot 30°= \frac{3,14}{60}=0,52$$
Mhh, und was sagen uns diese 0,52 jetzt? Das Ergebnis ist das Verhältnis von Bogenstück \( b \) zu Kreisradius \( r \) , also
$$\frac{b}{r}=0,52\ \rightarrow b=0,52\cdot r=0,52\cdot 2\mathrm{m}=1,04\mathrm{m}$$
Löst du die Gleichung nach \( b \) auf und setzt die \(2\mathrm{m}\) für den Radius ein, auf dem du läufst, kommt also in der Tat “etwas mehr als \(1\mathrm{m}\)” für die Strecke, die du auf der Kreisbahn laufen musst, heraus.
Zusammenfassung - Das Wichtigste in Kürze
Für die Angabe von Winkeln gibt es zwei verschiedene Vorgehensweisen und damit auch zwei Einheiten:
- Grad \( \rightarrow \) z.B. 60°
- das Bogenmaß als das Verhältnis zwischen Bogenstück \( \ {b} \) und dem Kreisradius \( \ {r} \) , welches in rad gemessen wird. Da ‘rad’ einheitenlos ist und nur dazu dient, bei einer Zahl zu kennzeichnen, dass es sich um ein Winkelmaß handelt, wird diese Einheit meist gar nicht angegeben \( \rightarrow \) \( \frac{ \pi}{2} \)

Grundgrößen, die bei der Umrechnung zwischen Winkeln in der Einheit Grad und rad benötigt werden
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2140/Grundgroessen_Umrechnung_Winkel_grad_rad.png
Mit dieser Formel kann zwischen dem Bogenmaß \( \mathrm{arc}\ \alpha \) und dem Winkel in Grad umgerechnet werden
$${\mathrm{arc}\ \alpha =\frac{b}{r} = \frac{\pi}{180°} \cdot \alpha}$$
oder in Worten
$${\mathrm{Winkel\ in\ rad\ }= \ \frac{\pi}{180°} \ \cdot \mathrm{Winkel\ in\ Grad}}$$
