Trigonometrie
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Trigonometrie |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 15:30 |
1. Einleitung Trigonometrie
Einleitung Trigonometrie
In dieser Lektion dreht sich alles um Trigonometrie.
Die Trigonometrie ist ein Teilgebiet der Mathematik. Der Name leitet sich von zwei griechischen Begriffen ab: Dreieck und Maß. Seitenlängen und Winkel sind die entscheidenden Größen, die das Aussehen eines Dreiecks bestimmen. Die Trigonometrie beschäftigt sich also damit, mathematische Beziehungen zwischen Seitenlängen und Winkeln beim Dreieck herzustellen.
Die Form des Dreiecks ist eine Form, die in vielen technischen Anwendungen immer wieder auftaucht. Ob als Geometrielement in technischen Konstruktionen wie einem Kran, einer Brücke oder für die Aufhängung eines Zeltes, als Element zur Darstellung von Oberflächen in Computerspiele, CAD-Anwendungen oder Berechnungsmodellen wie z.B. bei der Finite-Elemente-Modelle oder bei der Zerlegung eines Vektors in seine Komponenten.
Ganz anschaulich siehst du das sofort in den folgenden Bildern.
Schau doch einfach das nächste Mal, wenn du draußen unterwegs bist, wo du überall die Form des Dreiecks findest. Häufig sind es rechtwinklige Dreiecke, also Dreiecke, bei denen ein Winkel \( 90° \) hat. Allgemeine Dreiecke kommen aber ebenfalls immer wieder vor. In den folgenden Abschnitten lernst du die wichtigsten Größen und deren Zusammenhänge beim Dreieck kennen. Es ist sehr wichtig, dass du dich wirklich gut mit diesem Themengebiet auskennst. Die Kenntnisse sind einfach ein sehr grundlegendes Werkzeug, das immer und immer wieder gebraucht wird.
2. Gradmaß und Bogenmaß
Gradmaß und Bogenmaß
Dass Winkel in Grad also "°" angegeben werden, hast du in der Schule gelernt. Wenn du dich einmal komplett um deine Hochachse drehst, hast du dich um 360° gedreht. 360° sind also 'einmal rum'. Alle anderen Winkel lassen sich als Anteile von 360° angeben. Auf deinem Geodreieck zum Beispiel hat die eine Ecke 90° (das ist ein rechter Winkel) und die anderen beiden Ecken haben 45°. Die Einteilung auf dem Geodreieck ist typischer Weise in 1°-Schritten.
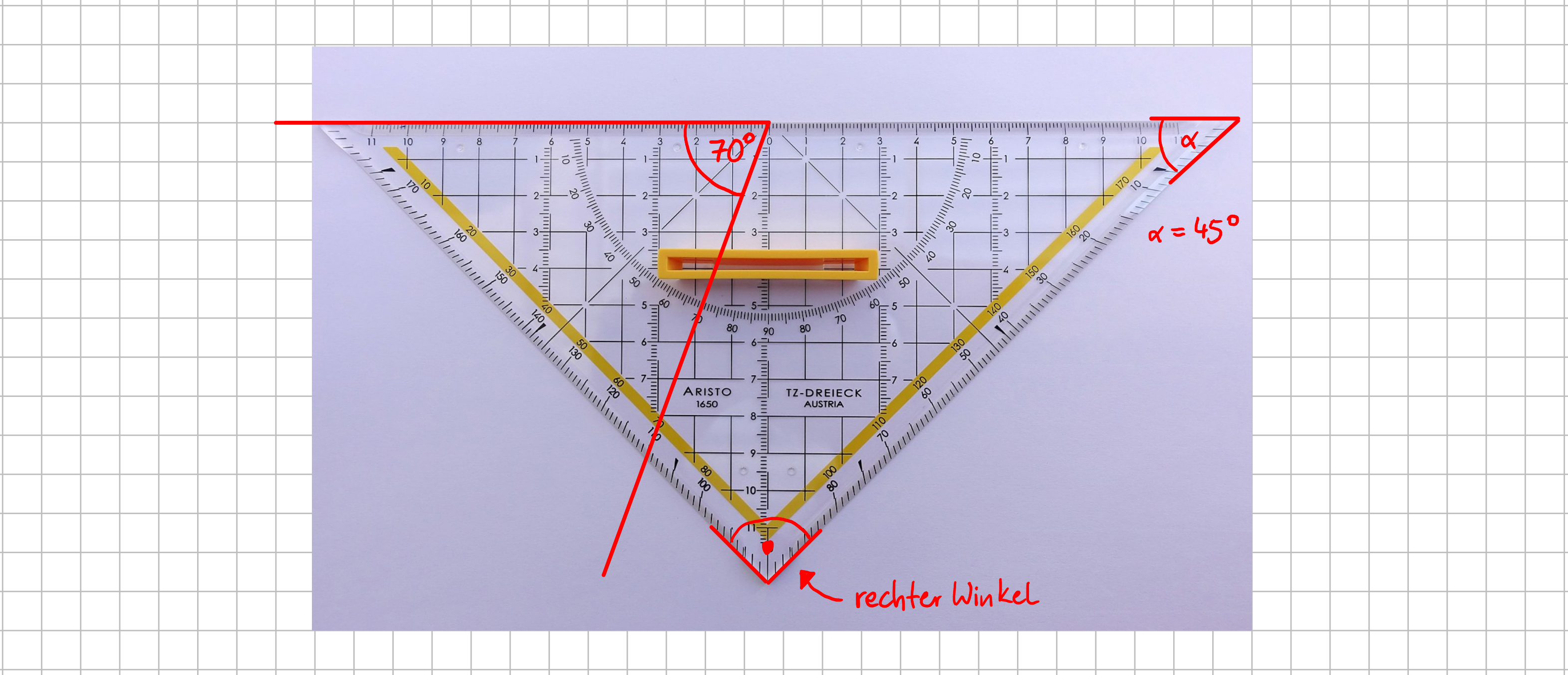
Typische Winkel und messen allgemeiner Winkel mit dem Geodreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg auf Basis von Kmtextor
CC BY-SA 4.0
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2140/Typische_Winkel_beim_Geodreieck.png
https://commons.wikimedia.org/w/index.php?curid=74388047
Jetzt kann man Winkel eben nicht nur in ° angeben, sondern auch über das Bogenstück, also die zum Winkel gehörende Strecke auf dem Kreis. In der folgenden Zeichnung ist ein Kreis mit dem Radius \( r \) dargestellt. Außerdem ist der Winkel \( \alpha \) eingezeichnet. Wenn der Radius \( r \) bekannt ist, kann man den Winkel statt über \( \alpha \) genauso gut über die Strecke \( b \) angeben.
Stell dir vor, du hast das Ende eines Seils irgendwo befestigt und hältst das andere Ende in der Hand am ausgestreckten Arm fest. Das Seil und dein ausgestreckter Arm sind zusammen so lang, dass zwischen dem Befestigungspunkt des Seils und deiner Körpermitte \(2\mathrm{m}\) liegen. Wenn du jetzt losläufst, musst du auf einem Kreis laufen. Und wenn du etwas mehr als \(1\mathrm{m}\) zurücklegst, hat das Seil einen Winkel von 30° überstrichen. “Wieso gerade \(1\mathrm{m}\)?”, fragst du? Lass uns doch einfach mal schauen, wie der Zusammenhang zwischen dem Winkel in ° und der Strecke \( b \) ist. (In der Zwischenzeit kannst du ja gerade mal den Versuch machen und nachmessen, ob \(1\mathrm{m}\) korrekt sind.)
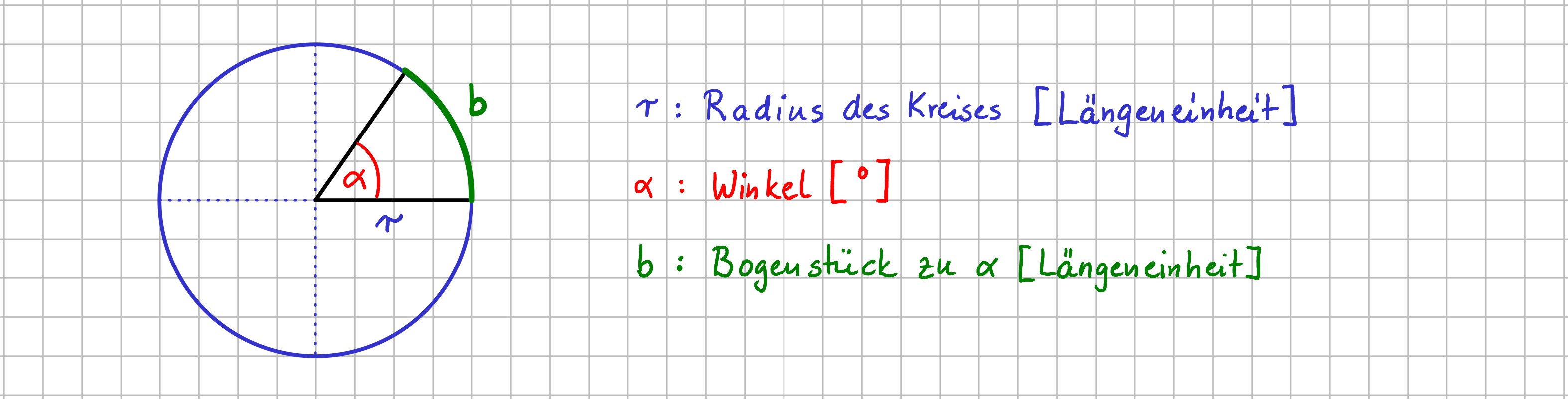
Grundgrößen, die bei der Umrechnung zwischen Winkeln in der Einheit Grad und rad benötigt werden
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2140/Grundgroessen_Umrechnung_Winkel_grad_rad.png
“Einmal rum” sind 360°. Das ist klar. Der Umfang eines Kreises, also die Strecke, wenn man einmal rum läuft, ist \( U = 2 \pi \cdot r \) lang. Das ist hoffentlich auch klar.
Wenn wir jetzt die beiden verschiedenen Arten von “einmal rum” ("einmal rum in ° " und “einmal rum als Bogenstück”) ins Verhältnis setzen, dann muss zwischen dem Winkel \( \alpha \) und der Strecke \( b \) dasselbe Verhältnis vorliegen, da "ein Stück rum in ° " gleich “ein Stück rum als Bogen” ist:
$$\frac{360°}{2\pi \cdot r} = \frac{\alpha}{b} \quad \rightarrow \quad \frac{180°}{\pi \cdot r} = \frac{\alpha}{b}$$
Wenn du diese Gleichung jetzt noch umstellst, um das Verhältnis aus \( b \) und \( r \) zu bekommen, dann steht da
$$\frac{b}{r}=\frac{\pi}{180°} \cdot \alpha$$
Das Verhältnis von Bogenstück zu Radius, also \( \frac{b}{r} \) wird als Bogenmaß des Winkels bezeichnet. Man schreibt dafür auch \( \mathrm{arc} \alpha \) . Es wird in der Einheit rad angegeben, auch wenn es formal einheitenlos ist. So kann man aber kennzeichnen, dass es sich bei der angegebenen Zahl um eine Winkelangabe handelt.
Ein Winkel von 1 rad liegt also genau dann vor, wenn der Radius \( r \) den Wert ‘1 Längeneinheit’ hat, du also auf einem Kreis mit einem Radius von \( r = 1\mathrm{m}\) auch genau \(1\mathrm{m}\) auf dem Umfang zurücklegst.
Für die Umrechnung gilt also
$${\mathrm{arc}\ \alpha =\frac{b}{r} = \frac{\pi}{180°} \cdot \alpha}$$
oder in Worten
$${\mathrm{Winkel\ in\ rad\ }= \ \frac{\pi}{180°} \ \cdot \mathrm{Winkel\ in\ Grad}}$$
Schauen wir uns jetzt nochmal das Beispiel mit dem Seil an. Du erinnerst dich: Du hast ein Seil in der Hand, dessen eines Ende festgemacht ist. Der Abstand zwischen diesem Punkt und deiner Körpermitte ist so, dass du dich auf einem Kreis mit dem Radius von \(2\mathrm{m}\) bewegst. Es soll ein Winkel von 30° überstrichen werden. Ich habe behauptet, dass du dafür “etwas mehr als \(1\mathrm{m}\)” auf der Kreisbahn gehen musst. Setzen wir also in die Formel ein:
$$\mathrm{Winkel\ in\ rad}=\frac{\pi}{180°}\cdot 30°= \frac{3,14}{60}=0,52$$
Mhh, und was sagen uns diese 0,52 jetzt? Das Ergebnis ist das Verhältnis von Bogenstück \( b \) zu Kreisradius \( r \) , also
$$\frac{b}{r}=0,52\ \rightarrow b=0,52\cdot r=0,52\cdot 2\mathrm{m}=1,04\mathrm{m}$$
Löst du die Gleichung nach \( b \) auf und setzt die \(2\mathrm{m}\) für den Radius ein, auf dem du läufst, kommt also in der Tat “etwas mehr als \(1\mathrm{m}\)” für die Strecke, die du auf der Kreisbahn laufen musst, heraus.
Zusammenfassung - Das Wichtigste in Kürze
Für die Angabe von Winkeln gibt es zwei verschiedene Vorgehensweisen und damit auch zwei Einheiten:
- Grad \( \rightarrow \) z.B. 60°
- das Bogenmaß als das Verhältnis zwischen Bogenstück \( \ {b} \) und dem Kreisradius \( \ {r} \) , welches in rad gemessen wird. Da ‘rad’ einheitenlos ist und nur dazu dient, bei einer Zahl zu kennzeichnen, dass es sich um ein Winkelmaß handelt, wird diese Einheit meist gar nicht angegeben \( \rightarrow \) \( \frac{ \pi}{2} \)

Grundgrößen, die bei der Umrechnung zwischen Winkeln in der Einheit Grad und rad benötigt werden
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2140/Grundgroessen_Umrechnung_Winkel_grad_rad.png
Mit dieser Formel kann zwischen dem Bogenmaß \( \mathrm{arc}\ \alpha \) und dem Winkel in Grad umgerechnet werden
$${\mathrm{arc}\ \alpha =\frac{b}{r} = \frac{\pi}{180°} \cdot \alpha}$$
oder in Worten
$${\mathrm{Winkel\ in\ rad\ }= \ \frac{\pi}{180°} \ \cdot \mathrm{Winkel\ in\ Grad}}$$
Arbeitsblatt - Teste dein Wissen
Aufgabe - Jetzt bist du dran
3. Who is who beim Dreieck
Who is who beim Dreieck
Als erstes wollen wir uns anschauen, welche Buchstaben typischer Weise verwendet werden, um die einzelnen Komponenten eines Dreiecks zu bezeichnen.
Es gibt einige Konventionen:
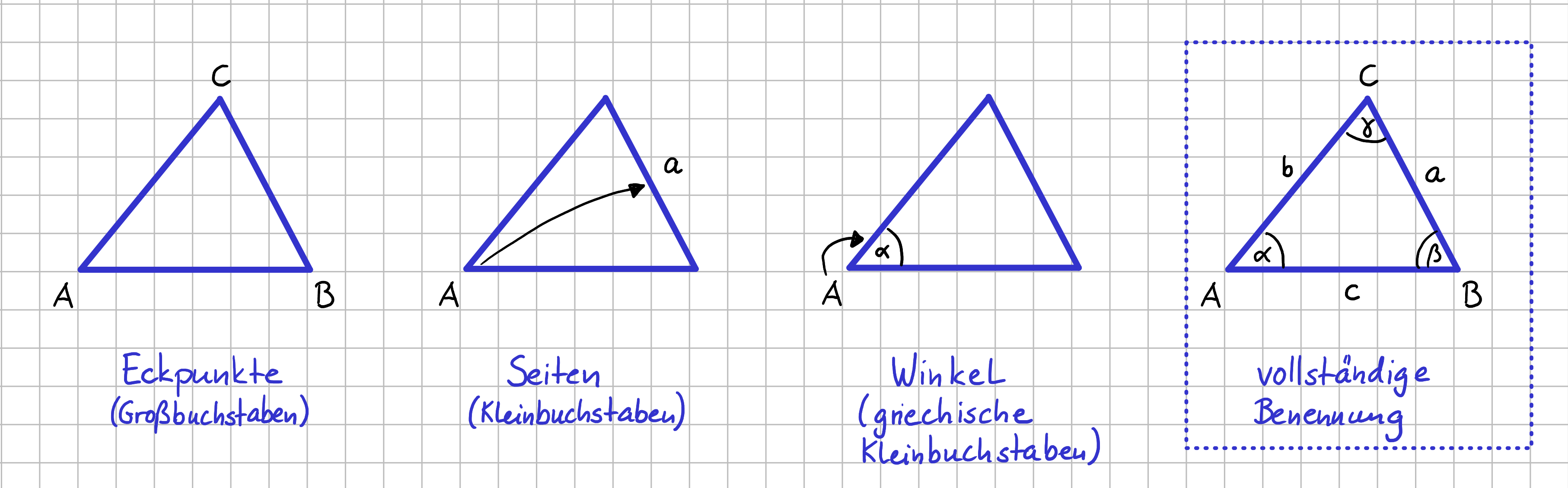
Konventionen für die Komponentenbezeichnung beim allgemeinen Dreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2136/Konventionen_Komponentenbezeichnung_allgemeines_Dreieck.png
- Die Eckpunkte eines Dreiecks werden mit Großbuchstaben bezeichnet. Dies geschieht meistens fortlaufend im mathematisch positiven Sinne, also gegen den Uhrzeigersinn.
- Die Seiten eines Dreiecks werden mit Kleinbuchstaben bezeichnet. Die einem Eckpunkt gegenüberliegende Seite bekommt als Bezeichnung den passenden Kleinbuchstaben.
- Für die Winkel werden griechische Buchstaben verwendet. Der Winkel bekommt typischer Weise den zur Bezeichnung des Eckpunktes passenden griechischen Buchstaben. Typische griechische Kleinbuchstaben sind
- \( \alpha \) alpha
- \( \beta \) beta
- \( \gamma \) gamma
- \( \delta \) delta
- \( \theta, \vartheta \) theta
- \( \pi \) = 180°
- \( \phi, \varphi \) phi
Manchmal gibt es zwei unterschiedliche Schreibweisen für die griechischen Buchstaben.
Zusammenfassung - Das Wichtigste in Kürze
Dies sind die Konventionen für die Bezeichnung der Komponenten eines Dreiecks:

Konventionen für die Komponentenbezeichnung beim allgemeinen Dreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2136/Konventionen_Komponentenbezeichnung_allgemeines_Dreieck.png
Aufgabe - Jetzt bist du dran
4. Rechtwinkliges Dreieck
Rechtwinkliges Dreieck
Rechtwinklige Dreiecke kommen erstaunlich häufig in der Praxis vor. Deswegen wollen wir uns ganz besonders um diese Spezies kümmern. Bevor wir auf die mathematischen Zusammenhänge schauen, die zwischen Seitenlängen und Winkeln bestehen, müssen wir uns erstmal auf eine gemeinsame Sprache verständigen.
Wie bei allen Disziplinen, ob beim Sport oder in der Mathematik, gibt es bestimmte Fachbegriffe, die verwendet werden. Welche sind das bei einem rechtwinkligen Dreieck, also bei einem Dreieck, das einen 90°-Winkel hat?
- Die Seite, die dem rechten Winkel gegenüber liegt, heißt Hypothenuse. Die Hypothenuse ist immer die längste Seite im rechtwinkligen Dreieck.
- Die beiden anderen Seiten heißen Katheten.
- Wird einer der beiden Winkel betrachtet, die nicht 90° haben gilt: Die Ankathete liegt am Winkel dran, die Gegenkathete liegt gegenüber dem Winkel.
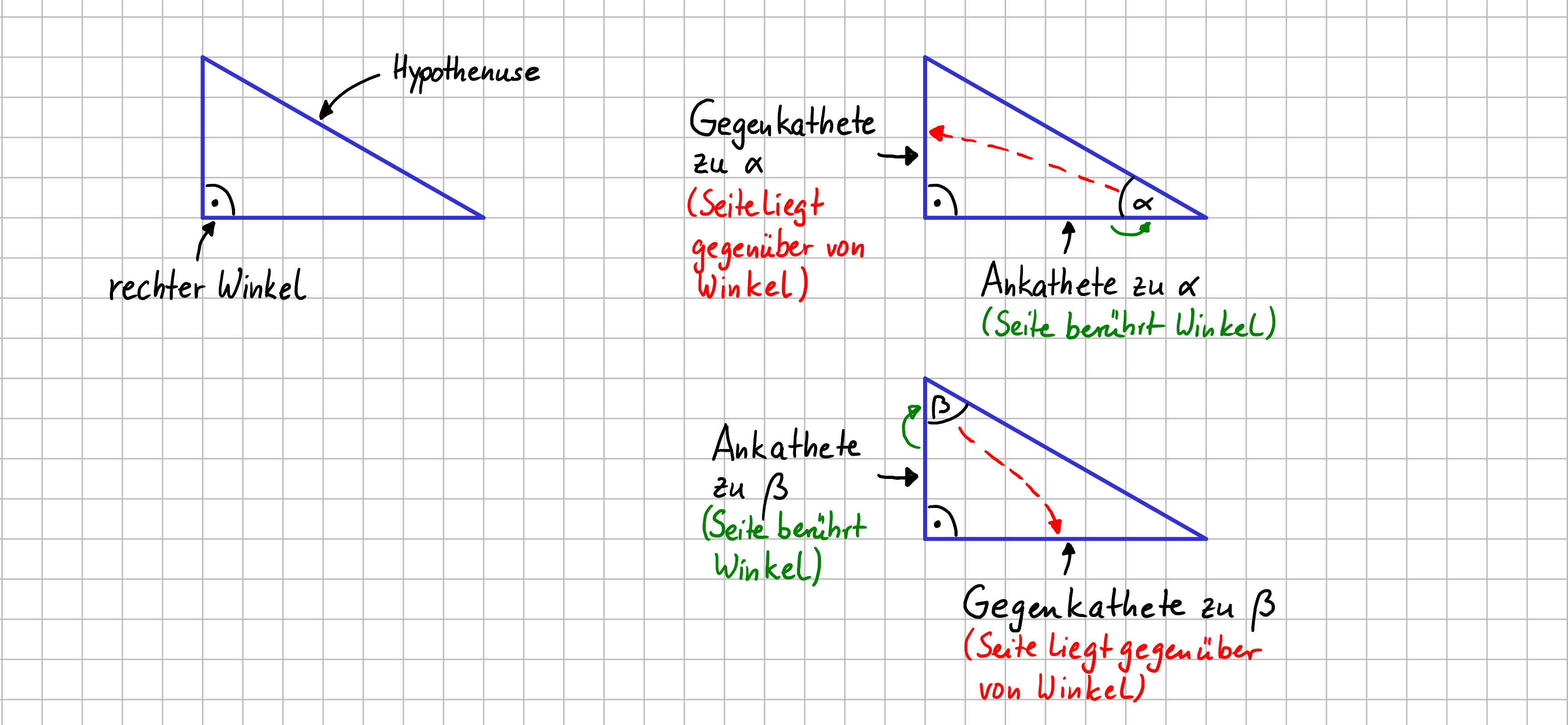
Schritt für Schritt: Konventionen für die Seitenbezeichnung beim rechtwinkligen Dreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2138/Schritt_fuer_Schritt_Konventionen_fuer_die_Bezeichnungen.png
- Oft wird in Herleitungen oder Formelsammlungen der Punkt, an dem der rechte Winkel liegt, mit \( C \) bezeichnet. Der rechte Winkel ist dann \( \gamma \) und \( c \) die Hypothenuse .
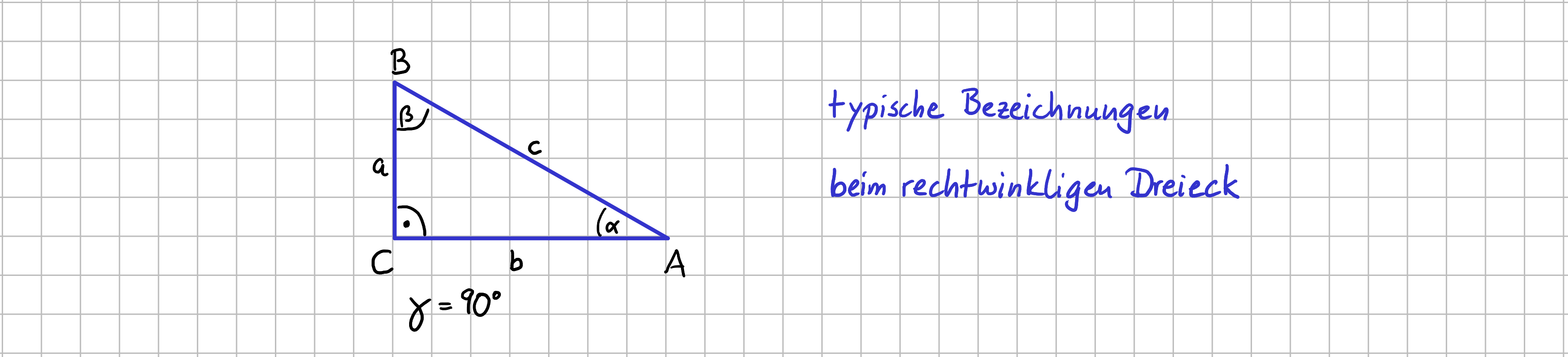
Standardzuordnung der Winkel beim rechtwinkligen Dreieck: \( \gamma \) ist der rechte Winkel
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2138/Standardzuordnung_der_Winkel_beim_rechtwinkligen_Dreieck.png
Zusammenfassung - Das Wichtigste in Kürze
Dies sind die Konventionen für die Bezeichnung der Seiten im rechtwinkligen Dreieck:
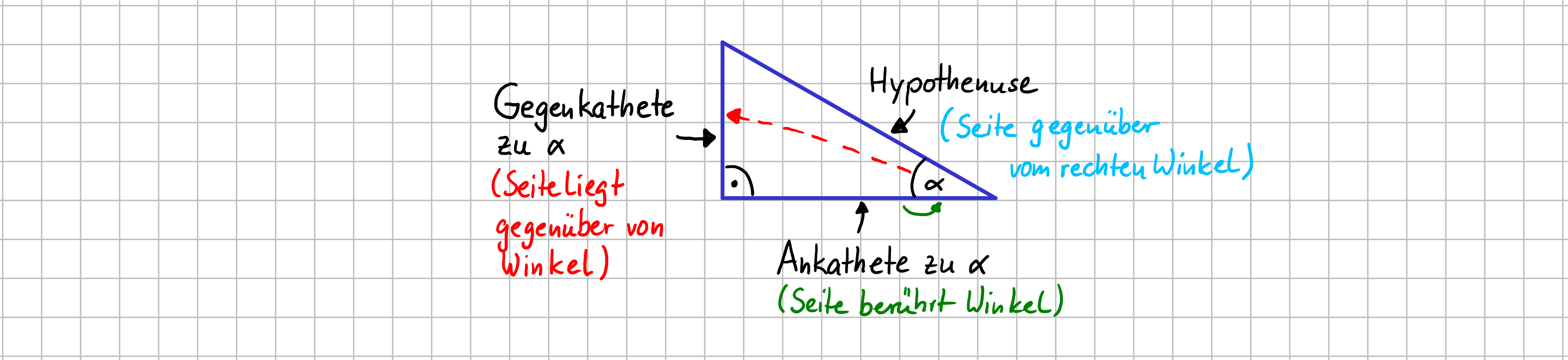
Konventionen für die Seitenbezeichnung beim rechtwinkligen Dreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2138/Konventionen_Seitenbezeichnungen_rechtwinkliges_Dreieck.png
- Die Seite, die dem rechten Winkel gegenüber liegt, heißt Hypothenuse. Die Hypothenuse ist immer die längste Seite im rechtwinkligen Dreieck.
- Die beiden anderen Seiten heißen Katheten.
- Wird einer der beiden Winkel betrachtet, die nicht 90° haben gilt: Die Ankathete liegt am Winkel dran, die Gegenkathete liegt gegenüber dem Winkel.
Aufgabe - Jetzt bist du dran
4.1. Satz des Pythagoras
Satz des Pythagoras
Für rechtwinklige Dreiecke gibt es einen ganz besonderen Zusammenhang zwischen den Längen der Seiten. Dieser Zusammenhang ist unter dem Namen Satz des Pythagoras bekannt.
Hier findest Du drei verschiedene Formulierungen für diesen Satz:
Variante 1:
Der Flächeninhalt des Quadrates über der einen Kathete plus der Flächeninhalt des Quadrates über der anderen Kathete ist gleich dem Flächeninhalt des Quadrates über der Hypothenuse.
Variante 2:
Die Länge der einen Kathete ins Quadrat plus der Länge der anderen Kathete ins Quadrat ist gleich der Länge der Hypothenuse ins Quadrat.
Variante 3:
Wenn mit \( c \) die Hypothenuse des rechtwinkligen Dreiecks bezeichnet ist \( a \) und \( b \) die beiden Katheten sind, gilt $$a^2+b^2=c^2$$
Welche Variante ist für dich am einfachsten zu merken? Damit meine ich: Mit welcher Variante verstehst du am besten, was die Aussage des Satzes des Pythagoras ist?
Im folgenden Bild ist Variante 1 graphisch veranschaulicht.
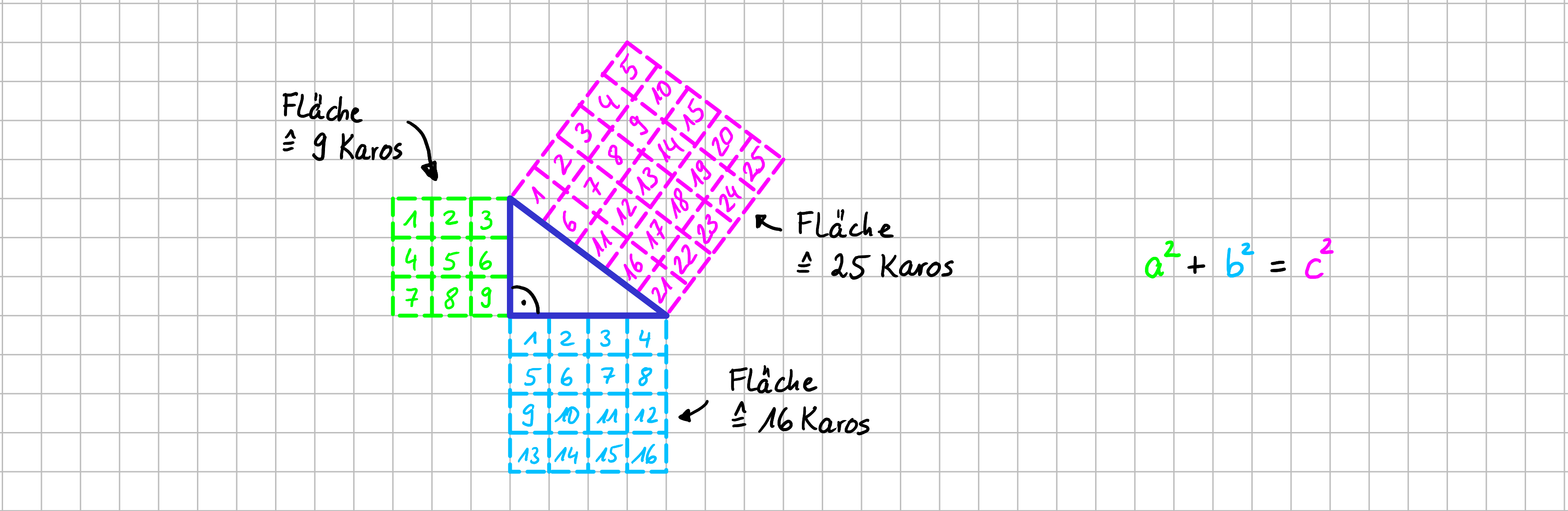
Satz des Pythagoras ausführlich
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2134/Satz_des_Pythagoras_ausfuehrlich.png
In vielen Anwendungen kommt der Satz des Pythagoras zum Einsatz, wenn es darum geht, eine Länge bei einem rechtwinkligen Dreieck zu bestimmen. Die Formel muss dann also noch nach der gesuchten Länge aufgelöst werden. Sind z.B. die Längen \( b \) und \( c \) bekannt, gilt für \( a \):
$$a=\sqrt{c^2-b^2}$$
Zahlenbeispiel

Satz des Pythagoras: Zahlenbeispiel
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2134/Satz_des_Pythagoras_Zahlenbeispiel.png
Zusammenfassung - Das Wichtigste in Kürze

Satz des Pythagoras kurz und knapp
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2134/Satz_des_Pythagoras_kurz_und_knapp.png
Arbeitsblatt - Teste dein Wissen
Aufgabe - Jetzt bist du dran
Tests
4.2. Sinus, Cosinus und Tangens
Winkelfunktionen Sinus, Cosinus und Tangens
Zwischen den Winkeln eines rechtwinkligen Dreiecks und den Seitenlängen gibt es feste Zusammenhänge. Sie werden durch die sogenannten Winkelfunktionen – Sinus-, Cosinus- und Tangens-Funktion – beschrieben.
Die Winkelfunktionen sind grundsätzlich für alle Winkelwerte, also von 0° bis 360° bzw. von 0 bis 2\( \pi \) definiert. Beim Anwendungsfall des rechtwinkligen Dreiecks werden nur Werte von 0° bis 90° bzw. von 0 bis \( \frac{\pi}{2} \) auftreten. In diesem Winkelbereich solltest du dich also besonders gut mit den Winkelfunktionen auskennen.
Wir betrachten das rechtwinklige Dreieck, wie es in der folgenden Abbildung links dargestellt ist. Für den Winkel \( \alpha \) ist die Sinus-Funktion definiert als das Verhältnis der Längen von Gegenkathete (G) und Hypothenuse (H). Die Cosinus-Funktion ist definiert als das Verhältnis der Längen von Ankathete (A) und Hypothenuse (H).
Da die Hypothenuse immer die längste Seite im rechtwinkligen Dreieck ist, ist sofort klar, dass sowohl die Werte der Sinus- als auch der Cosinus-Funktion immer kleiner oder gleich 1 sind, da ja in beiden Fällen durch die Länge der Hypothenuse geteilt wird.
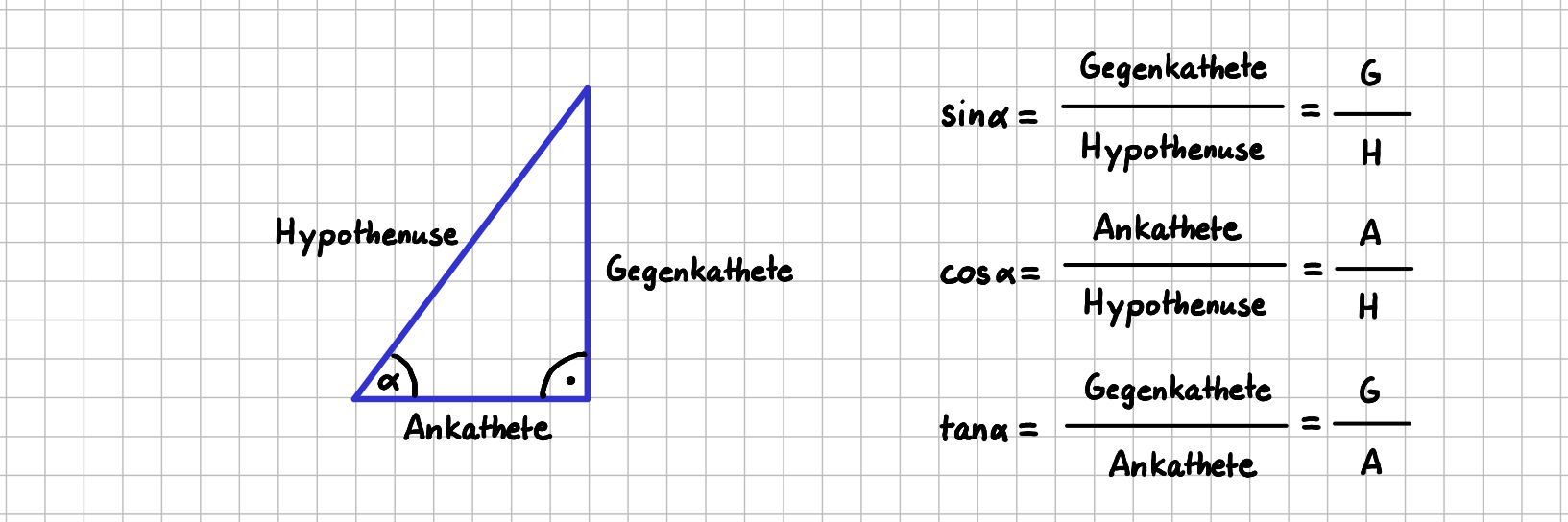
Definition der Winkelfunktionen Sinus, Cosinus und Tangens
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Definition_der_Winkelfunktionen.png
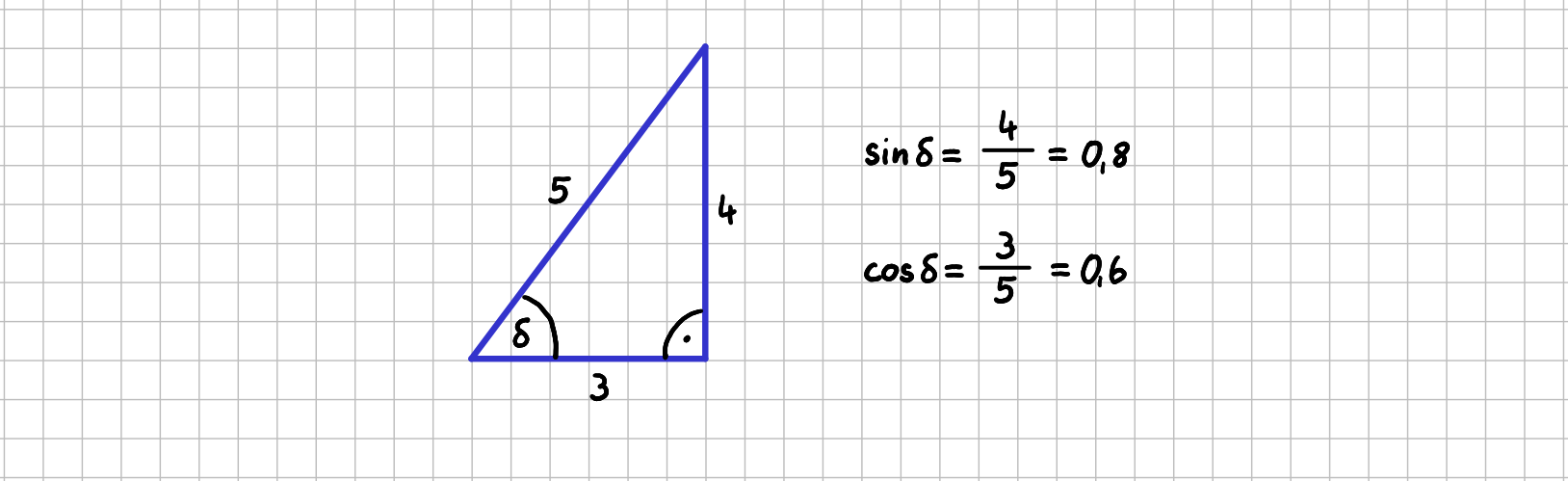
Zahlenbeispiel zur Bestimmung von Sinus und Cosinus
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Zahlenbeispiel_Bestimmung_der_Winkelfunktionen.png
Wenn du "G durch H" teilst, erhältst du \( \frac{4}{5} \) oder 0,8. Das ist der Wert des Sinus von \( \gamma \). Wenn du "A durch H" teilst, erhältst du \( \frac{3}{5} \) oder 0,6. Das ist der Wert des Cosinus von \( \gamma \). Es sind wie erwartet beides Werte kleiner 1.
Merkregeln
Um sich bei Sinus und Co zu merken, wer denn nun durch was geteilt wird, gibt es verschiedene Merkregeln. Vielleicht hast du in der Schule die "GAGA H ühner H of AG" kennengelernt. Wenn nicht, schau doch einfach mal im Netz, wie diese Regel funktioniert.
a) die musikalische Variante
Ich selbst mache mir es ganz einfach. Ich merke mir: "Sinus und Cosinus sind 'Irgendwas geteilt durch die Hypothenuse'. Bleibt noch die Frage, wie merke ich mir, was 'Irgendwas' ist. Ganz einfach: Beim Sinus denke ich an sinGen. Und schon weiß ich, dass der Sinus mit der Gegenkathete zusammengehört. Also ist "Sinus = Gegenkathete durch Hypothenuse". Dann bleibt für den Cosinus "Cosinus = Ankathete durch Hypothenuse".
Beim Tangens funktoniert es ganz ähnlich. Ich weiß, dass Ankathete und Gegenkathete im Spiel sind. Stellt sich die Frage: Wer steht oberhalb des Bruchstrichs? Auch da hilft mit ein Wort aus der Musik: tanGo. Also steht die Gegenkathete oben und es gilt "Tanges = Gegenkathete durch Ankathete" und das ist nichts anderes als "Tangens = Sinus durch Cosinus".
b) die kuschelige Variante
Im Englischen heißt "cosy" so etwas wie kuschelig (oder gemütlich). Da die Ankathete am Winkel kuschelt, kannst du dir hierüber auch ganz einfach merken, dass die Cosinusfunktion mit der Ankathete verknüpft ist.
Wertebereich
Wie sieht denn nun der Wertebereich für die Sinus- und die Cosinusfunktion aus? Das lässt sich am einfachsten am Einheitskreis veranschaulichen. Der Einheitskreis ist schlicht und einfach ein Kreis mit Radius \(1\). Wenn du an einer beliebigen Stelle den Radius einzeichnest und dann mit der passenden Horizontale und Vertikale ein rechtwinkliges Dreieck, wie in der folgenden Abbildung darstelllt zeichnest, kannst du die Werte für \(\sin \alpha\) und \(\cos\alpha\) sofort als Längen der Ankathete (schwarz eingezeichnet) und der Gegenkathete (grün eingezeichnet) zum Winkel \( \alpha\) ablesen. Die Hypothenuse hat ja die Länge \(1\).
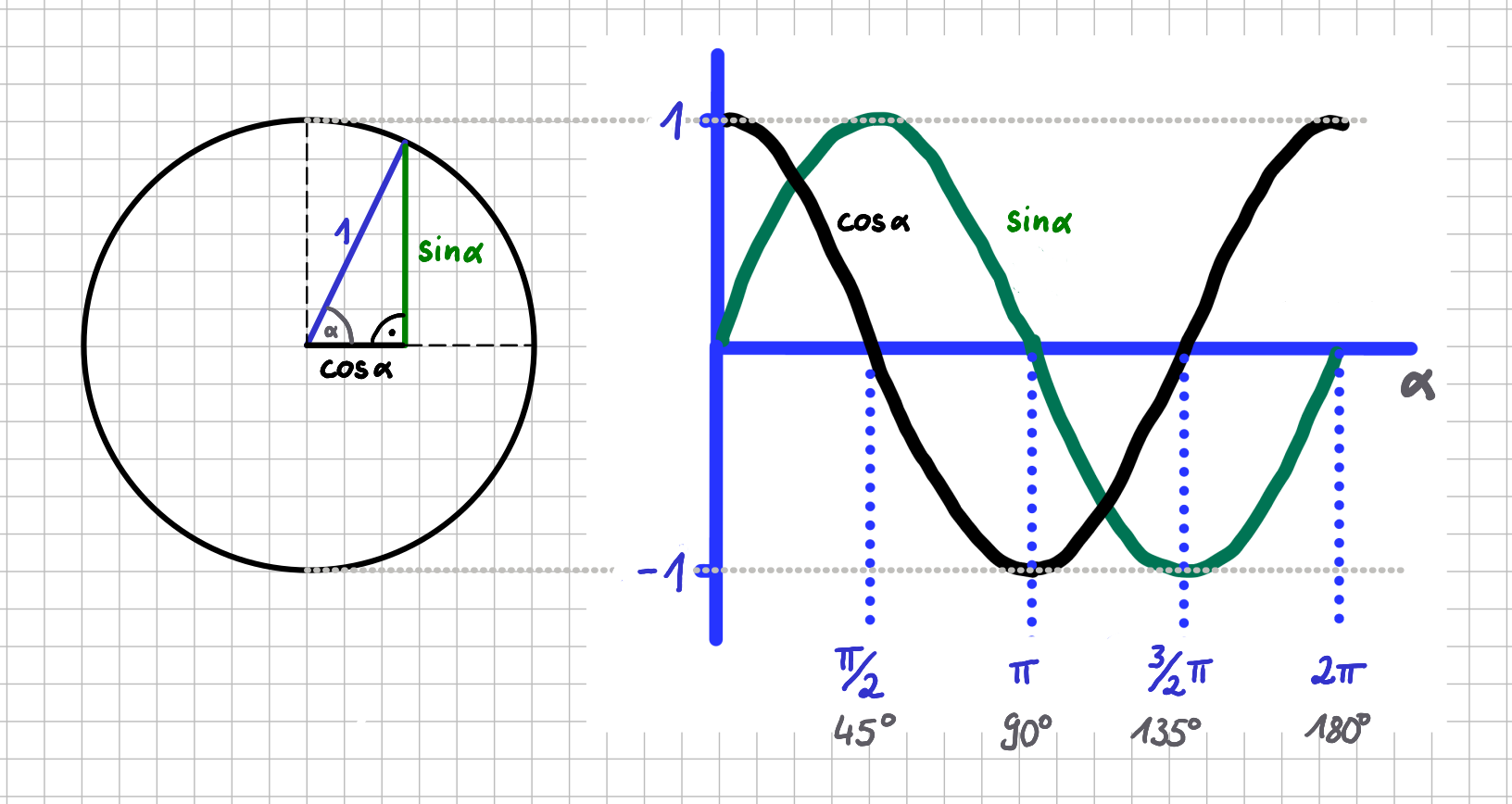
Einheitskreis: Wertebereich und Werte von Sinus- und Cosinusfunktion
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Sinus_und_cosinus_am_Einheitskreis.png
Wenn du jetzt für viele verschiedene Winkelwerte von \( \alpha\) die Längen der beiden Seiten im Dreieck abliest und in ein Diagramm zeichnest, bekommst du den in der Abbildung rechts gezeichneten Verlauf für die Sinus- und die Cosinusfunktion.
Aus der Darstellung mit dem Einheitskreis ist sofort zu sehen, dass zum Beispiel \(\sin 0° =0\) und \(\cos 0° =1\) gelten muss. Genauso siehst du sofort, dass \(\sin 90° =1\) und \(\cos 90° =1\) sein muss. Außerdem können beide Winkelfunktionen nur Werte zwischen \(1\) und \(-1\) annehmen.
Standardwerte
Es gibt Standardgrößen von Winkeln, die immer wieder auftauchen: 0°, 30°, 45° 60° und 90°. Für diese Winkel lohnt es sich, wenn du dir die Werte für die Sinus- und Cosinusfunktion merkst.
Es gibt eine ganz einfach Merkregel für diese Werte, genauer gesagt dafür, wie du eine Tabelle aufschreiben kannst, in der alle Werte der Winkelfunktionen für die Standardwinkel drinstehen. Und das geht in drei Schritten so:
Schritt 1:
Schreibe eine Tabelle wie diese auf:
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | |||||
| \( \cos \alpha \) |
Schritt 2:
Fülle die Tabelle von links nach rechts für \( \sin \alpha) \) aus. Jeder Eintrag besteht aus dem Faktor \( \frac{1}{2} \) mal einem Wurzelterm; die Zahl unter der Wurzel beginnt bei 0 erhöht sich immer um 1.
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | \( \frac{1}{2} \sqrt{0} \) |
\( \frac{1}{2} \sqrt{1} \) |
\( \frac{1}{2} \sqrt{2} \) |
\( \frac{1}{2} \sqrt{3} \) |
\( \frac{1}{2} \sqrt{4} \) |
| \( \cos \alpha \) |
Schritt 3:
Fülle die Tabelle für \( \cos \alpha \) aus. Nimm dazu die Einträge, die du gerade für die Sinuswerte eingetragen hast und trage sie jetzt andersrum, also rechts nach links in die Tabelle ein. Das sieht dann so aus:
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | \( \frac{1}{2} \sqrt{0} \) |
\( \frac{1}{2} \sqrt{1} \) |
\( \frac{1}{2} \sqrt{2} \) |
\( \frac{1}{2} \sqrt{3} \) |
\( \frac{1}{2} \sqrt{4} \) |
| \( \cos \alpha \) | \( \frac{1}{2} \sqrt{4} \) | \( \frac{1}{2} \sqrt{3} \) | \( \frac{1}{2} \sqrt{2} \) | \( \frac{1}{2} \sqrt{1} \) | \( \frac{1}{2} \sqrt{0} \) |
Und schon hast du die Wertetabelle fertig. War doch eigentlich ganz einfach, oder?
Wenn du jetzt denkst: "Warum soll ich denn Null so umständlich als \( \frac{1}{2}\sqrt{0} \) schreiben?" ..... Weil du's kannst. Und weil es Teil der Merkregel ist. Natürlich lassen sich einige Werte in der Tabelle noch vereinfachen. Das sieht dann so aus.
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \(\sin \alpha \) | 0 |
\( \frac{1}{2} \) |
\( \frac{\sqrt{2}}{2} \) |
\( \frac{\sqrt{3}}{2} \) |
1 |
| \( \cos \alpha \) | 1 | \( \frac{\sqrt{3}}{2} \) |
\( \frac{\sqrt{2}}{2} \) | \( \frac{1}{2} \) |
0 |
In dieser Darstellung wirst du die Tabelle meistens in Formelsammlungen finden. Jetzt weißt du aber auch, wie du dir die Werte ganz einfach merken kannst.
Und es schadet auch nicht, die Werte mal in Kommadarstellung gesehen zu haben. Das sieht dann so aus.
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | 0 |
0,5 |
0,707 |
0,866 |
1 |
| \( \cos \alpha \) | 1 | 0,866 |
0,707 |
0,5 |
0 |
Du kannst ja jede Zahl mit \(1\) malnehmen, ohne ihren Wert zu ändern. Die Zahl \(1\) kannst du ja auch als \(\dfrac{\sqrt2}{\sqrt2}\) darstellen.
Damit gilt also
Exkurs zu Umkehrfunktionen ... bzw. der Tatsache, dass man sie beim Lösen von Mechanikaufgaben sehr selten braucht.
Natürlich gibt es für die trigonometrischen Funktionen auch die Umkehrfunktionen. Schauen wir uns das einmal anhand der Cosinusfunktion an. Gegeben sei
$$\cos\varphi=\frac{\sqrt{3}}{2}$$
Um den Winkel 𝜑 zu berechnen, brauchen wir die Umkehrfunktion zur Cosinusfunktion. Das ist die Arcuscosinus-Funktion.
$$\varphi=\arccos\frac{\sqrt{3}}{2}=60°$$
Genauso gibt es die Arcussinus- und die Arcustangens-Funktion. Mit ihnen ist es möglich, den entsprechenden Wert des Winkels zu bestimmen.
In der Anwendung ist es oft gar nicht erforderlich, den wirklichen Winkelwert, also die Gradzahl, zu kennen. Oft reicht es aus, den Wert des Sinus oder Cosinus eines Winkels zu kennen. Hier kommen zwei Beispiele.
Beispiel 1:
Die Kräfte \( A \) und \(B\) sollen in ihre Komponenten bezüglich des gegebenen Koordinatensystems zerlegt werden. Die zugehörigen Winkel \( \beta \) und \(\gamma\) sind gegeben.
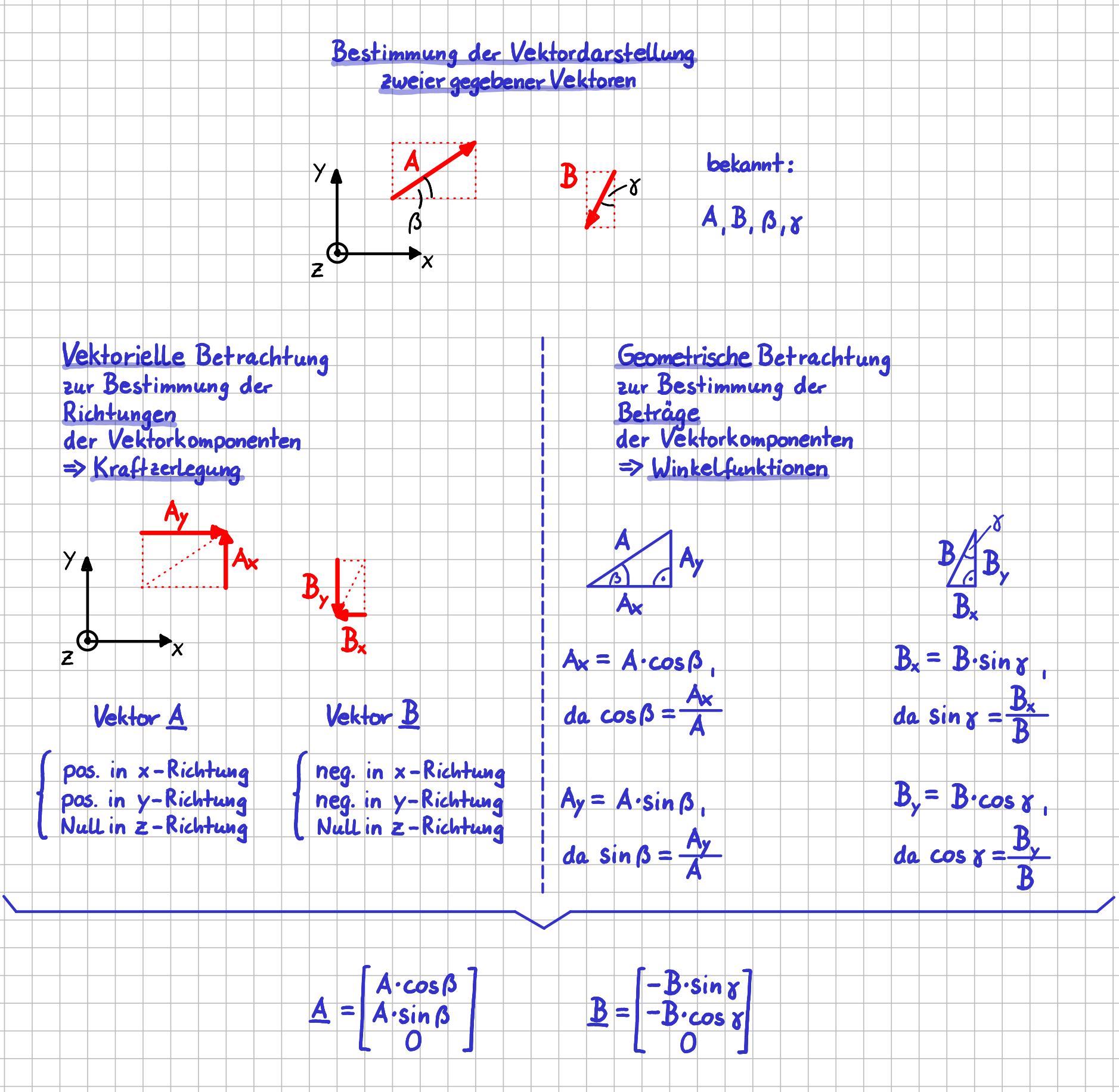
Komponentenzerlegung zweier Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Komponentenzerlegung_zweier_Vektoren.png
Es werden also "nur" die Winkelfunktionen \( \cos \beta \) und \( \sin \beta \) bzw. \( \cos \gamma \) und \( \sin \gamma\) und nicht die Winkel \( \beta \) und \( \gamma \) selbst benötigt.
Beispiel 2:
Um den Momentenvektor der Kraft \( F \) bzgl. Punkt \(B\) berechnen zu können, wird der Hebelarm benötigt. Er lässt sich unter Verwendung der Winkelfunktionen einfach angeben.
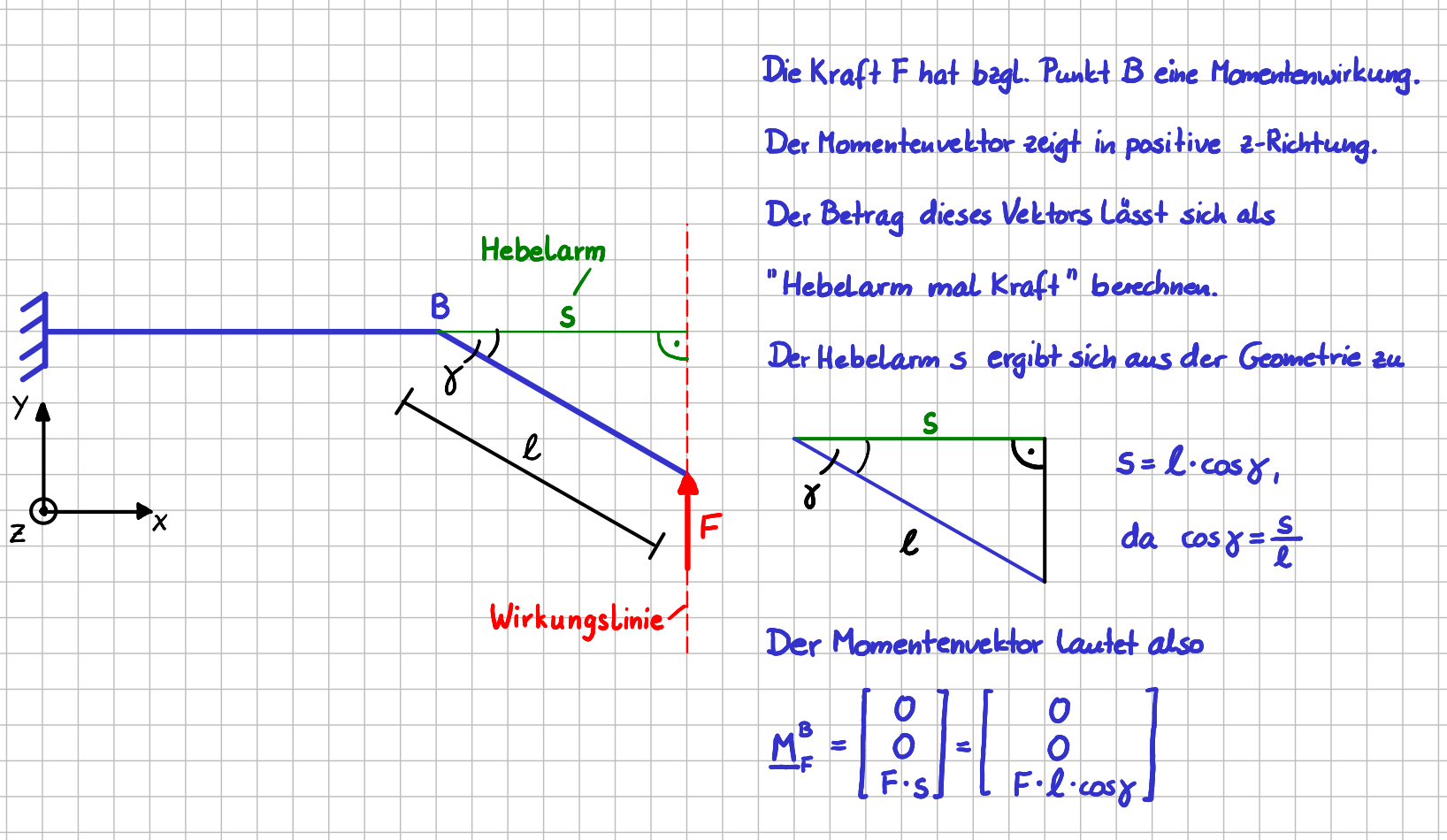
Bestimmung des Hebelarms einer Kraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Bestimmung_des_Hebelarms_einer_Kraft.png
Es wird also "nur" die Winkelfunktion \( \cos \gamma \) und nicht der Winkel \( \gamma \) selbst benötigt.
Ein kleiner Hinweis für alle (werdenden) Mechanikliebhaberinnen und Mechanikliebhaber: Es lohnt sich mit etwas mehr Übung gleich "sehen" zu können, dass im zweiten Beispiel \( s = l \cdot \cos \gamma \) gilt, ohne, dass man erst \( \cos \gamma = \frac{s}{l} \) hinschreiben muss. Es ist ja logisch, dass \( s \) also die Ankathete von \( \gamma \) , mit dem Cosinus zusammenhängt. Deshalb gilt "s ist gleich Hypothenuse mal Cosinus von Gamma".
Zusammenfassung - Das Wichtigste in Kürze
- Definition der Winkelfunktionen:
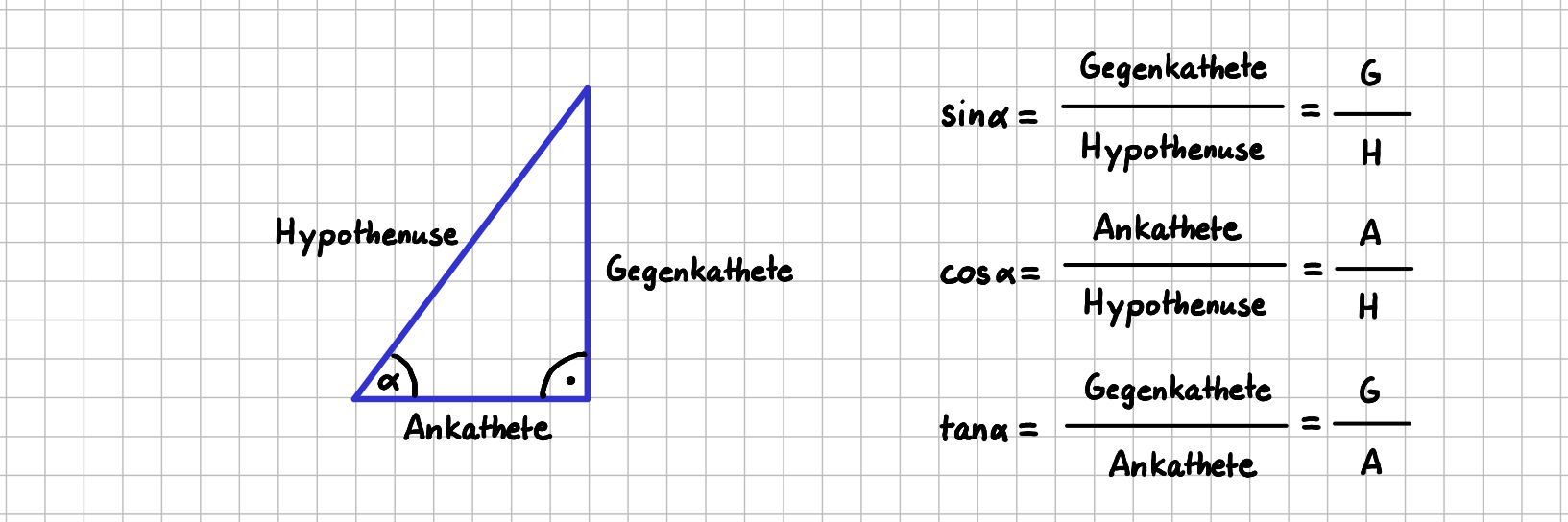
Definition der Winkelfunktionen Sinus, Cosinus und Tangens
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Definition_der_Winkelfunktionen.png
- An der Darstellung eines rechtwinkligen Dreiecks im Einheitskreis kannst du direkt die Werte für \(\sin \alpha\) und \(\cos \alpha\) für beliebige Winkel \( \alpha \) ablesen. Auch, wie der Verlauf der beiden grundlegenden Winkelfunktionen aussehen muss, ist sofort klar:

Einheitskreis: Wertebereich und Werte von Sinus- und Cosinusfunktion
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Sinus_und_cosinus_am_Einheitskreis.png
Der Wertebereich ist also auf \(-1\) bis \(1\) beschränkt.
- Zahlenwerte für Standardwinkel
-
0° 30° 45° 60° 90° \( \sin \alpha \) 0 \( \frac{1}{2} = 0,5 \) \( \frac{\sqrt{2}}{2} = 0,707\) \( \frac{\sqrt{3}}{2} = 0,866\) 1 \( \cos \alpha \) 1 \( \frac{\sqrt{3}}{2} = 0,866\) \( \frac{\sqrt{2}}{2} = 0,707\) \( \frac{1}{2} = 0,5 \) 0
Aufgabe - Jetzt bist du dran
Tests
5. Allgemeines Dreieck
Allgemeines Dreieck
Im allgemeinen Dreieck gibt es – bis auf die Winkelsumme – keinerlei Vorgaben für die Winkel.
Damit es übersichtlich bleibt, sind hier noch einmal die bereits eingeführten Bezeichnungen dargestellt. Sie gelten für alle folgenden Unterabschnitte.
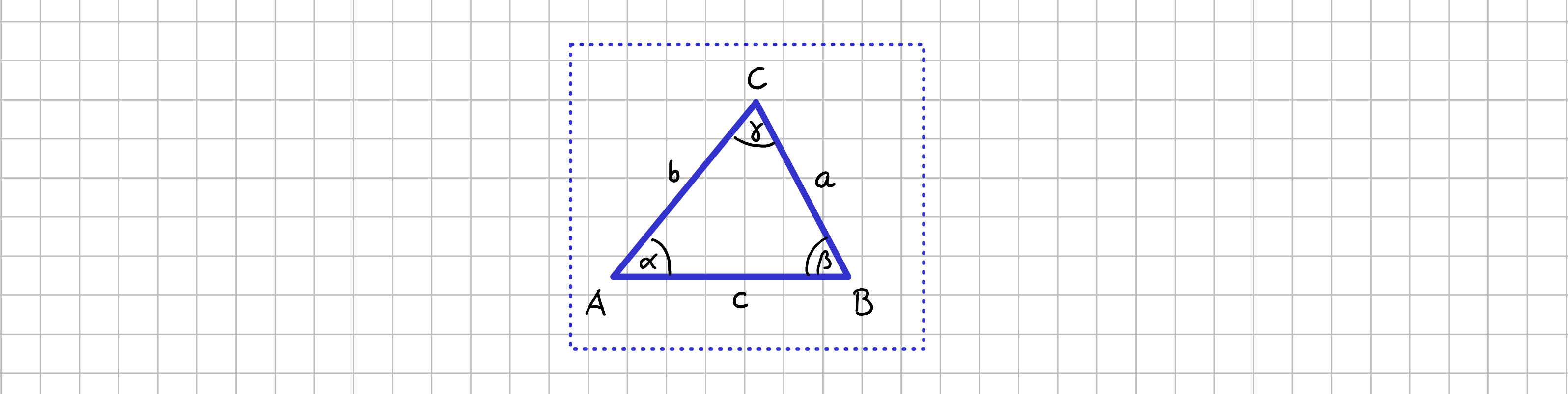
Standardbezeichnungen beim Dreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2137/Standardbezeichnungen_beim_Dreieck.png
Die Winkelsumme
Die Summe aller Winkel in einem Dreieck beträgt immer 180°:
$$\alpha + \beta + \gamma =180°$$
Der Sinussatz
Das Verhältnis aus dem Sinus eines Winkels und der Länge der dem Winkel gegenüberliegenden Seite ist konstant:
$$\frac{\sin\alpha}{a} = \frac{\sin\beta}{b} = \frac{\sin\gamma}{c}$$
Der Cosinussatz
Auch für das allgemeine Dreieck gibt es einen Zusammenhang zwischen den Quadraten der dre Seitenlängen. Er lautet:
$$c^2=a^2+b^2-2ab\cos\gamma$$
Für den Fall, dass \( \gamma = 90° \) gilt, ist \( \cos(90°) = 0 \) und der hintere Term verschwindet. Wenn es sich um ein rechtwinkliges Dreieck handelt, wird der Cosinussatz also zum Satz des Pythagoras.
Zusammenfassung - Das Wichtigste in Kürze
- Winkelsumme: \( \alpha + \beta + \gamma =180° \)
- Sinussatz: \( \dfrac{\sin\alpha}{a} = \dfrac{\sin\beta}{b} = \dfrac{\sin\gamma}{c} \)
- Cosinussatz: \( c^2=a^2+b^2-2ab\cos\gamma \)

Standardbezeichnungen beim Dreieck
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2137/Standardbezeichnungen_beim_Dreieck.png

