Trigonometrie
Trigonometrie
4. Rechtwinkliges Dreieck
4.2. Sinus, Cosinus und Tangens
Winkelfunktionen Sinus, Cosinus und Tangens
Zwischen den Winkeln eines rechtwinkligen Dreiecks und den Seitenlängen gibt es feste Zusammenhänge. Sie werden durch die sogenannten Winkelfunktionen – Sinus-, Cosinus- und Tangens-Funktion – beschrieben.
Die Winkelfunktionen sind grundsätzlich für alle Winkelwerte, also von 0° bis 360° bzw. von 0 bis 2\( \pi \) definiert. Beim Anwendungsfall des rechtwinkligen Dreiecks werden nur Werte von 0° bis 90° bzw. von 0 bis \( \frac{\pi}{2} \) auftreten. In diesem Winkelbereich solltest du dich also besonders gut mit den Winkelfunktionen auskennen.
Wir betrachten das rechtwinklige Dreieck, wie es in der folgenden Abbildung links dargestellt ist. Für den Winkel \( \alpha \) ist die Sinus-Funktion definiert als das Verhältnis der Längen von Gegenkathete (G) und Hypothenuse (H). Die Cosinus-Funktion ist definiert als das Verhältnis der Längen von Ankathete (A) und Hypothenuse (H).
Da die Hypothenuse immer die längste Seite im rechtwinkligen Dreieck ist, ist sofort klar, dass sowohl die Werte der Sinus- als auch der Cosinus-Funktion immer kleiner oder gleich 1 sind, da ja in beiden Fällen durch die Länge der Hypothenuse geteilt wird.
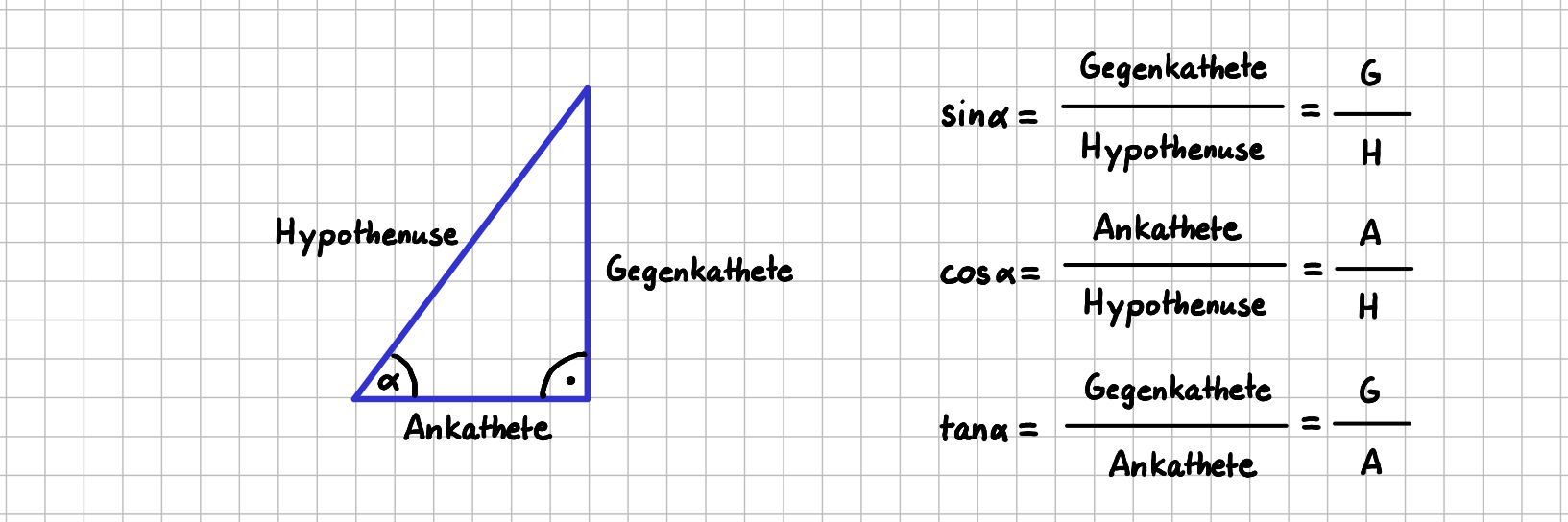
Definition der Winkelfunktionen Sinus, Cosinus und Tangens
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Definition_der_Winkelfunktionen.png
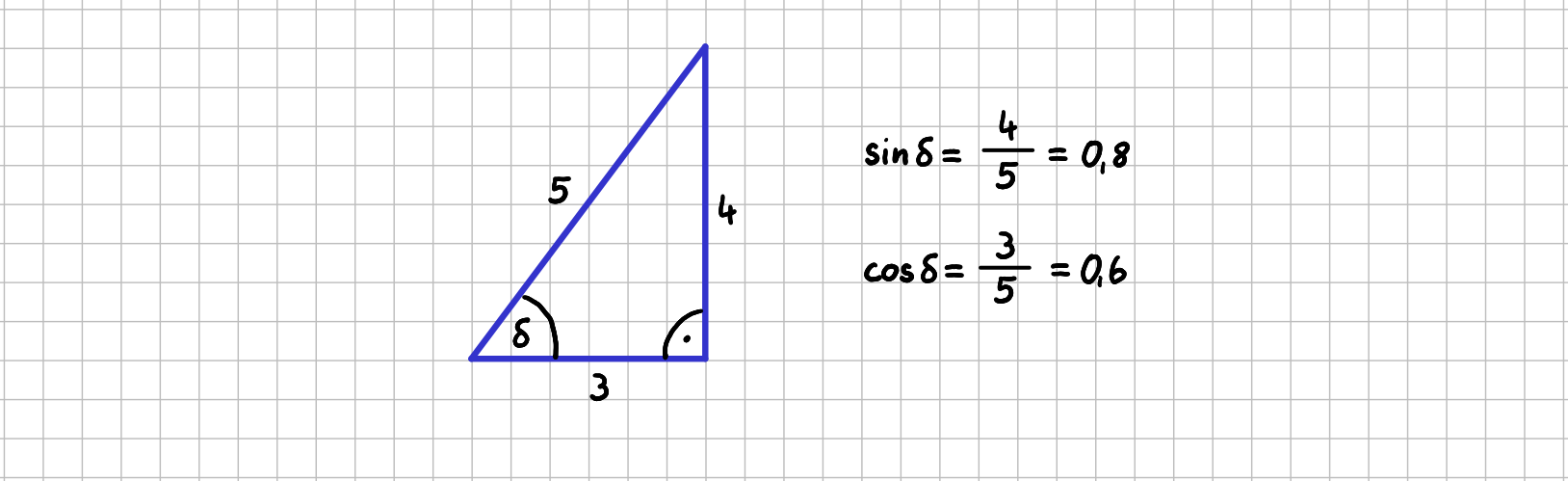
Zahlenbeispiel zur Bestimmung von Sinus und Cosinus
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Zahlenbeispiel_Bestimmung_der_Winkelfunktionen.png
Wenn du "G durch H" teilst, erhältst du \( \frac{4}{5} \) oder 0,8. Das ist der Wert des Sinus von \( \gamma \). Wenn du "A durch H" teilst, erhältst du \( \frac{3}{5} \) oder 0,6. Das ist der Wert des Cosinus von \( \gamma \). Es sind wie erwartet beides Werte kleiner 1.
Merkregeln
Um sich bei Sinus und Co zu merken, wer denn nun durch was geteilt wird, gibt es verschiedene Merkregeln. Vielleicht hast du in der Schule die "GAGA H ühner H of AG" kennengelernt. Wenn nicht, schau doch einfach mal im Netz, wie diese Regel funktioniert.
a) die musikalische Variante
Ich selbst mache mir es ganz einfach. Ich merke mir: "Sinus und Cosinus sind 'Irgendwas geteilt durch die Hypothenuse'. Bleibt noch die Frage, wie merke ich mir, was 'Irgendwas' ist. Ganz einfach: Beim Sinus denke ich an sinGen. Und schon weiß ich, dass der Sinus mit der Gegenkathete zusammengehört. Also ist "Sinus = Gegenkathete durch Hypothenuse". Dann bleibt für den Cosinus "Cosinus = Ankathete durch Hypothenuse".
Beim Tangens funktoniert es ganz ähnlich. Ich weiß, dass Ankathete und Gegenkathete im Spiel sind. Stellt sich die Frage: Wer steht oberhalb des Bruchstrichs? Auch da hilft mit ein Wort aus der Musik: tanGo. Also steht die Gegenkathete oben und es gilt "Tanges = Gegenkathete durch Ankathete" und das ist nichts anderes als "Tangens = Sinus durch Cosinus".
b) die kuschelige Variante
Im Englischen heißt "cosy" so etwas wie kuschelig (oder gemütlich). Da die Ankathete am Winkel kuschelt, kannst du dir hierüber auch ganz einfach merken, dass die Cosinusfunktion mit der Ankathete verknüpft ist.
Wertebereich
Wie sieht denn nun der Wertebereich für die Sinus- und die Cosinusfunktion aus? Das lässt sich am einfachsten am Einheitskreis veranschaulichen. Der Einheitskreis ist schlicht und einfach ein Kreis mit Radius \(1\). Wenn du an einer beliebigen Stelle den Radius einzeichnest und dann mit der passenden Horizontale und Vertikale ein rechtwinkliges Dreieck, wie in der folgenden Abbildung darstelllt zeichnest, kannst du die Werte für \(\sin \alpha\) und \(\cos\alpha\) sofort als Längen der Ankathete (schwarz eingezeichnet) und der Gegenkathete (grün eingezeichnet) zum Winkel \( \alpha\) ablesen. Die Hypothenuse hat ja die Länge \(1\).
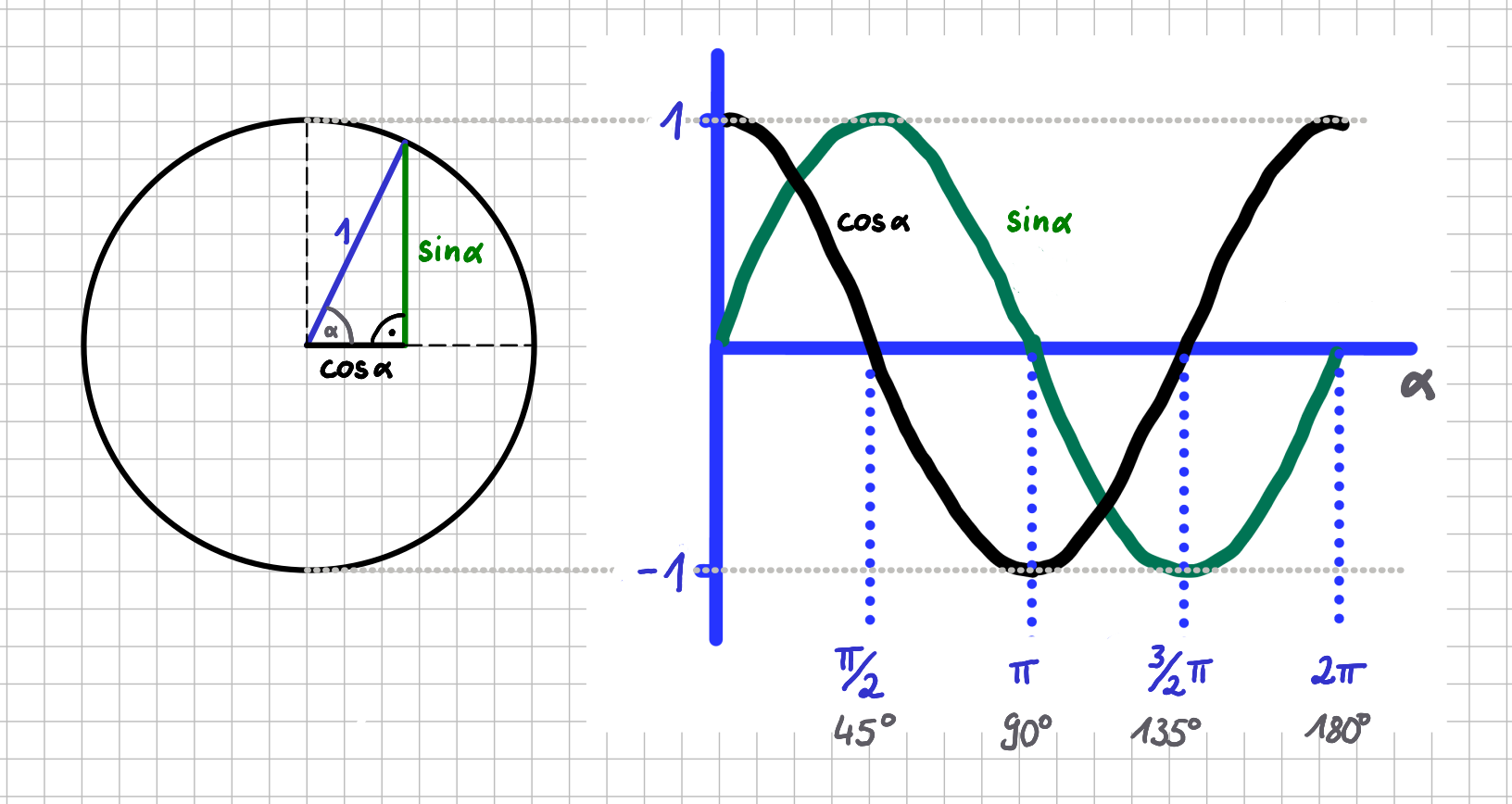
Einheitskreis: Wertebereich und Werte von Sinus- und Cosinusfunktion
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Sinus_und_cosinus_am_Einheitskreis.png
Wenn du jetzt für viele verschiedene Winkelwerte von \( \alpha\) die Längen der beiden Seiten im Dreieck abliest und in ein Diagramm zeichnest, bekommst du den in der Abbildung rechts gezeichneten Verlauf für die Sinus- und die Cosinusfunktion.
Aus der Darstellung mit dem Einheitskreis ist sofort zu sehen, dass zum Beispiel \(\sin 0° =0\) und \(\cos 0° =1\) gelten muss. Genauso siehst du sofort, dass \(\sin 90° =1\) und \(\cos 90° =1\) sein muss. Außerdem können beide Winkelfunktionen nur Werte zwischen \(1\) und \(-1\) annehmen.
Standardwerte
Es gibt Standardgrößen von Winkeln, die immer wieder auftauchen: 0°, 30°, 45° 60° und 90°. Für diese Winkel lohnt es sich, wenn du dir die Werte für die Sinus- und Cosinusfunktion merkst.
Es gibt eine ganz einfach Merkregel für diese Werte, genauer gesagt dafür, wie du eine Tabelle aufschreiben kannst, in der alle Werte der Winkelfunktionen für die Standardwinkel drinstehen. Und das geht in drei Schritten so:
Schritt 1:
Schreibe eine Tabelle wie diese auf:
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | |||||
| \( \cos \alpha \) |
Schritt 2:
Fülle die Tabelle von links nach rechts für \( \sin \alpha) \) aus. Jeder Eintrag besteht aus dem Faktor \( \frac{1}{2} \) mal einem Wurzelterm; die Zahl unter der Wurzel beginnt bei 0 erhöht sich immer um 1.
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | \( \frac{1}{2} \sqrt{0} \) |
\( \frac{1}{2} \sqrt{1} \) |
\( \frac{1}{2} \sqrt{2} \) |
\( \frac{1}{2} \sqrt{3} \) |
\( \frac{1}{2} \sqrt{4} \) |
| \( \cos \alpha \) |
Schritt 3:
Fülle die Tabelle für \( \cos \alpha \) aus. Nimm dazu die Einträge, die du gerade für die Sinuswerte eingetragen hast und trage sie jetzt andersrum, also rechts nach links in die Tabelle ein. Das sieht dann so aus:
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | \( \frac{1}{2} \sqrt{0} \) |
\( \frac{1}{2} \sqrt{1} \) |
\( \frac{1}{2} \sqrt{2} \) |
\( \frac{1}{2} \sqrt{3} \) |
\( \frac{1}{2} \sqrt{4} \) |
| \( \cos \alpha \) | \( \frac{1}{2} \sqrt{4} \) | \( \frac{1}{2} \sqrt{3} \) | \( \frac{1}{2} \sqrt{2} \) | \( \frac{1}{2} \sqrt{1} \) | \( \frac{1}{2} \sqrt{0} \) |
Und schon hast du die Wertetabelle fertig. War doch eigentlich ganz einfach, oder?
Wenn du jetzt denkst: "Warum soll ich denn Null so umständlich als \( \frac{1}{2}\sqrt{0} \) schreiben?" ..... Weil du's kannst. Und weil es Teil der Merkregel ist. Natürlich lassen sich einige Werte in der Tabelle noch vereinfachen. Das sieht dann so aus.
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \(\sin \alpha \) | 0 |
\( \frac{1}{2} \) |
\( \frac{\sqrt{2}}{2} \) |
\( \frac{\sqrt{3}}{2} \) |
1 |
| \( \cos \alpha \) | 1 | \( \frac{\sqrt{3}}{2} \) |
\( \frac{\sqrt{2}}{2} \) | \( \frac{1}{2} \) |
0 |
In dieser Darstellung wirst du die Tabelle meistens in Formelsammlungen finden. Jetzt weißt du aber auch, wie du dir die Werte ganz einfach merken kannst.
Und es schadet auch nicht, die Werte mal in Kommadarstellung gesehen zu haben. Das sieht dann so aus.
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| \( \sin \alpha \) | 0 |
0,5 |
0,707 |
0,866 |
1 |
| \( \cos \alpha \) | 1 | 0,866 |
0,707 |
0,5 |
0 |
Du kannst ja jede Zahl mit \(1\) malnehmen, ohne ihren Wert zu ändern. Die Zahl \(1\) kannst du ja auch als \(\dfrac{\sqrt2}{\sqrt2}\) darstellen.
Damit gilt also
Exkurs zu Umkehrfunktionen ... bzw. der Tatsache, dass man sie beim Lösen von Mechanikaufgaben sehr selten braucht.
Natürlich gibt es für die trigonometrischen Funktionen auch die Umkehrfunktionen. Schauen wir uns das einmal anhand der Cosinusfunktion an. Gegeben sei
$$\cos\varphi=\frac{\sqrt{3}}{2}$$
Um den Winkel 𝜑 zu berechnen, brauchen wir die Umkehrfunktion zur Cosinusfunktion. Das ist die Arcuscosinus-Funktion.
$$\varphi=\arccos\frac{\sqrt{3}}{2}=60°$$
Genauso gibt es die Arcussinus- und die Arcustangens-Funktion. Mit ihnen ist es möglich, den entsprechenden Wert des Winkels zu bestimmen.
In der Anwendung ist es oft gar nicht erforderlich, den wirklichen Winkelwert, also die Gradzahl, zu kennen. Oft reicht es aus, den Wert des Sinus oder Cosinus eines Winkels zu kennen. Hier kommen zwei Beispiele.
Beispiel 1:
Die Kräfte \( A \) und \(B\) sollen in ihre Komponenten bezüglich des gegebenen Koordinatensystems zerlegt werden. Die zugehörigen Winkel \( \beta \) und \(\gamma\) sind gegeben.
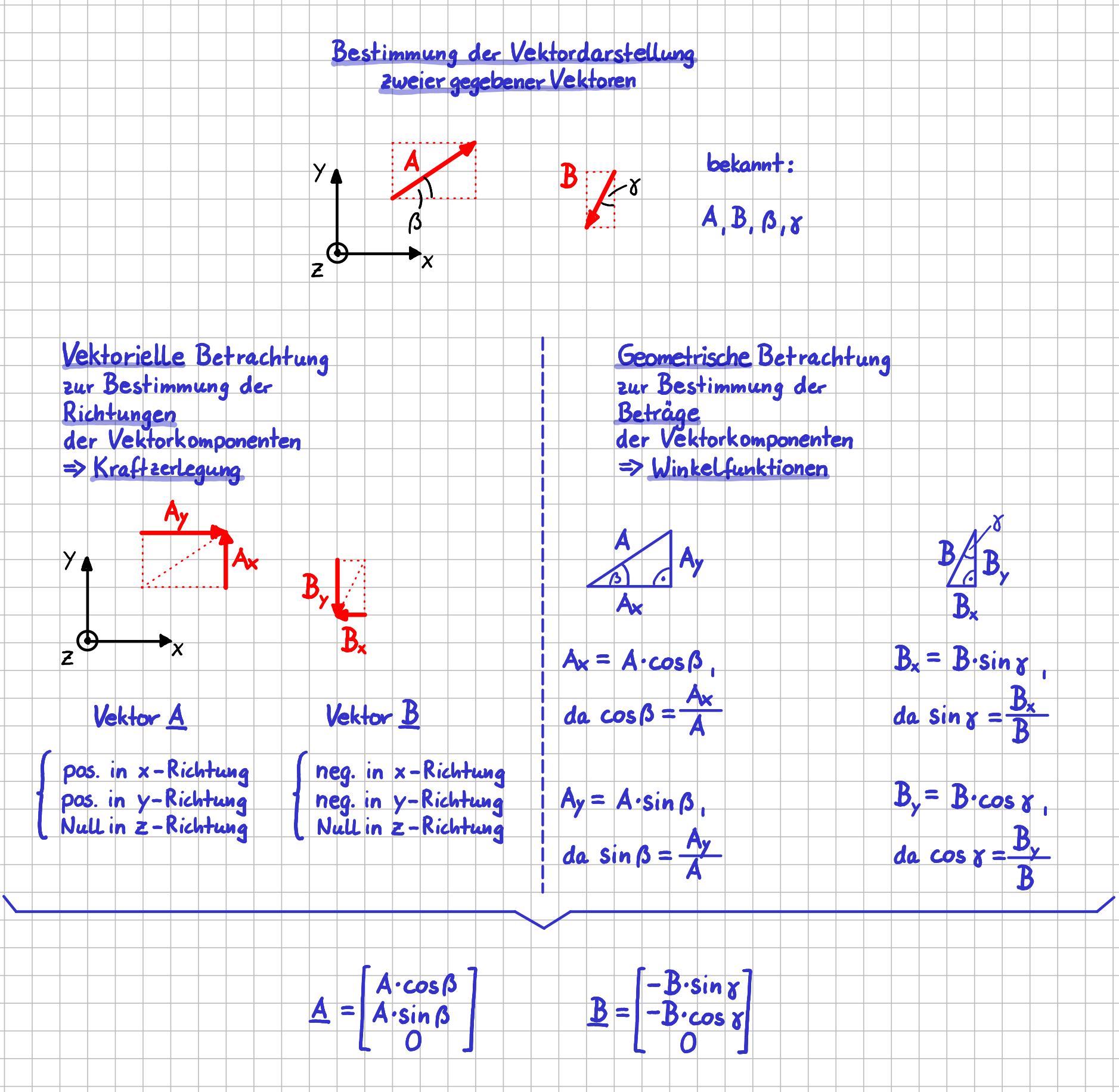
Komponentenzerlegung zweier Vektoren
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Komponentenzerlegung_zweier_Vektoren.png
Es werden also "nur" die Winkelfunktionen \( \cos \beta \) und \( \sin \beta \) bzw. \( \cos \gamma \) und \( \sin \gamma\) und nicht die Winkel \( \beta \) und \( \gamma \) selbst benötigt.
Beispiel 2:
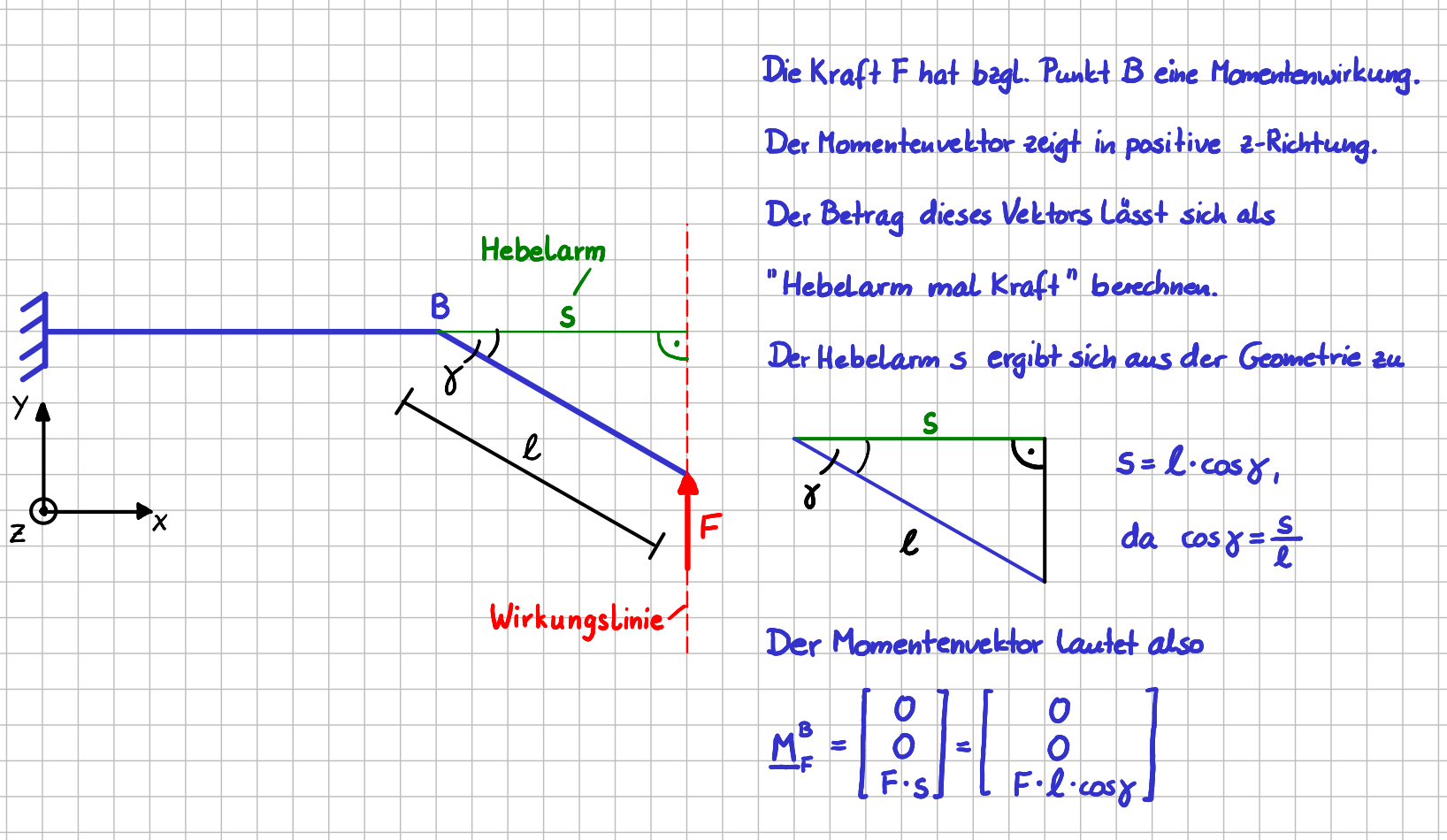
Um den Momentenvektor der Kraft \( F \) bzgl. Punkt \(B\) berechnen zu können, wird der Hebelarm benötigt. Er lässt sich unter Verwendung der Winkelfunktionen einfach angeben.
Bestimmung des Hebelarms einer Kraft
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Bestimmung_des_Hebelarms_einer_Kraft.png
Es wird also "nur" die Winkelfunktion \( \cos \gamma \) und nicht der Winkel \( \gamma \) selbst benötigt.
Ein kleiner Hinweis für alle (werdenden) Mechanikliebhaberinnen und Mechanikliebhaber: Es lohnt sich mit etwas mehr Übung gleich "sehen" zu können, dass im zweiten Beispiel \( s = l \cdot \cos \gamma \) gilt, ohne, dass man erst \( \cos \gamma = \frac{s}{l} \) hinschreiben muss. Es ist ja logisch, dass \( s \) also die Ankathete von \( \gamma \) , mit dem Cosinus zusammenhängt. Deshalb gilt "s ist gleich Hypothenuse mal Cosinus von Gamma".
Zusammenfassung - Das Wichtigste in Kürze
- Definition der Winkelfunktionen:
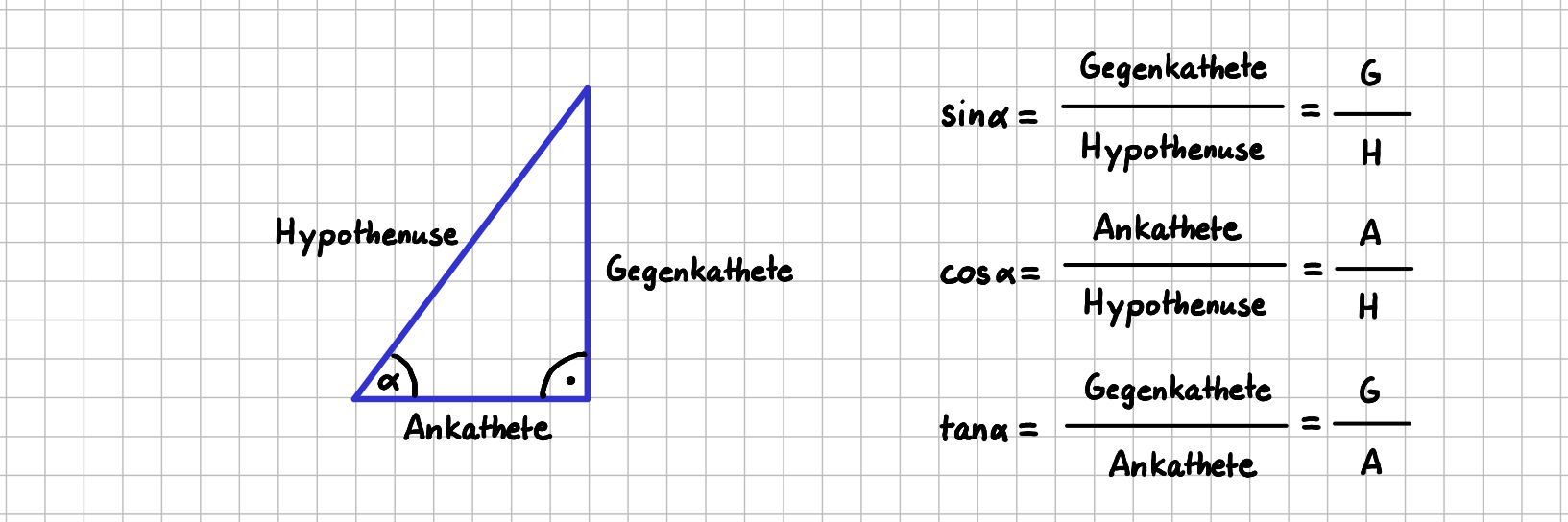
Definition der Winkelfunktionen Sinus, Cosinus und Tangens
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Definition_der_Winkelfunktionen.png
- An der Darstellung eines rechtwinkligen Dreiecks im Einheitskreis kannst du direkt die Werte für \(\sin \alpha\) und \(\cos \alpha\) für beliebige Winkel \( \alpha \) ablesen. Auch, wie der Verlauf der beiden grundlegenden Winkelfunktionen aussehen muss, ist sofort klar:

Einheitskreis: Wertebereich und Werte von Sinus- und Cosinusfunktion
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2135/Sinus_und_cosinus_am_Einheitskreis.png
Der Wertebereich ist also auf \(-1\) bis \(1\) beschränkt.
- Zahlenwerte für Standardwinkel
-
0° 30° 45° 60° 90° \( \sin \alpha \) 0 \( \frac{1}{2} = 0,5 \) \( \frac{\sqrt{2}}{2} = 0,707\) \( \frac{\sqrt{3}}{2} = 0,866\) 1 \( \cos \alpha \) 1 \( \frac{\sqrt{3}}{2} = 0,866\) \( \frac{\sqrt{2}}{2} = 0,707\) \( \frac{1}{2} = 0,5 \) 0
