Schnittgrößen
Schnittgrößen
2. Was sind Schnittgrößen?
Was sind Schnittgrößen?
Wird ein Balken von außen belastet, treten in seinem Inneren Kräfte und Momente auf. Es ist wichtig, diese inneren Größen berechnen zu können. Nur so kann die Tragfähigkeit von Tragwerken untersucht oder zum Beispiel der erforderliche Querschnitt eines Balkens festgelegt, also dimensioniert werden.
Wie Reaktionsgrößen bei Lagern werden innere Kräfte und Momente durch Freischneiden sichtbar. Deswegen werden diese Größen zusammen auch als Schnittgrößen bezeichnet.
Der Wert der Schnittgrößen ist in der Regel davon abhängig, an welcher Stelle entlang seiner Länge der Balken geschnitten wird.
Konvention für das Koordinatensystem
Bevor wir den ersten Balken durchschneiden, um das sichtbar machen zu können, was in seinem Inneren passiert, lohnt es sich, dass wir uns erstmal auf ein paar Konventionen einigen. Die erste Konvention betrifft die Wahl des Koordinatensystems. Bei Balken hat man sich auf Folgendes verständigt:
1. Der Ursprung des Koordinatensystems liegt an einem Ende des Balkens.
2. Die \( x \)-Achse zeigt läuft entlang der Balkenachse, so dass \( x \) nur den Wert Null oder positive Werte haben kann.
3. Die \( z \)-Achse zeigt senkrecht dazu "nach unten" und liegt in der Bildebene.
4. Die \( y \)-Achse zeigt demnach gemäß der Rechte-Hand-Regel für Koordinatensysteme aus der Bildebene heraus.
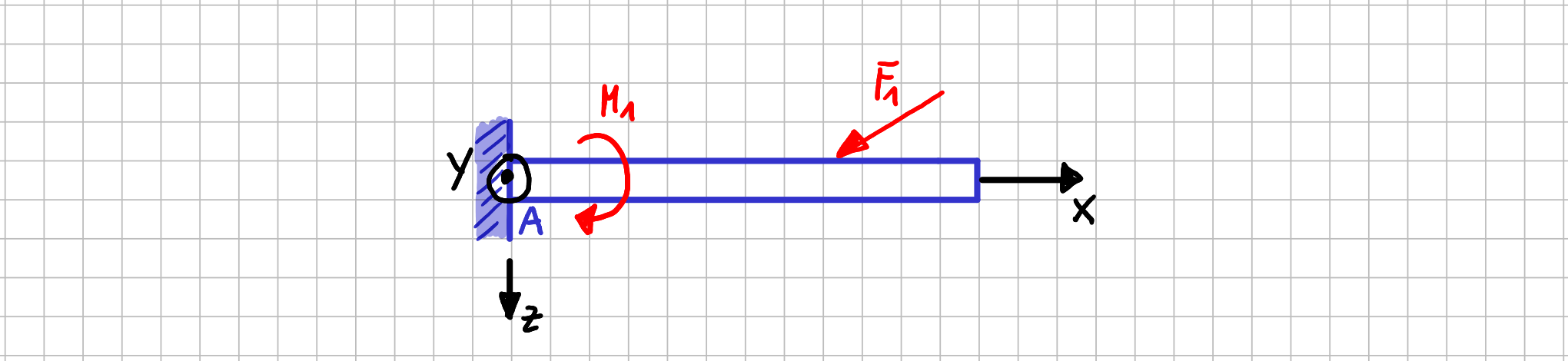
Konvention für das Koordinatensystem beim Balken
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Konvention_KOS_Balken.png
Konvention für die Schnittufer
Wird ein Balken an einer beliebigen Stelle entlang seiner Länge senkrecht zu seiner Hauptrichtung geschnitten, entstehen zwei Teilsysteme.
Im folgenden Beispiel gibt es ein linkes und ein rechtes Teilsystem.
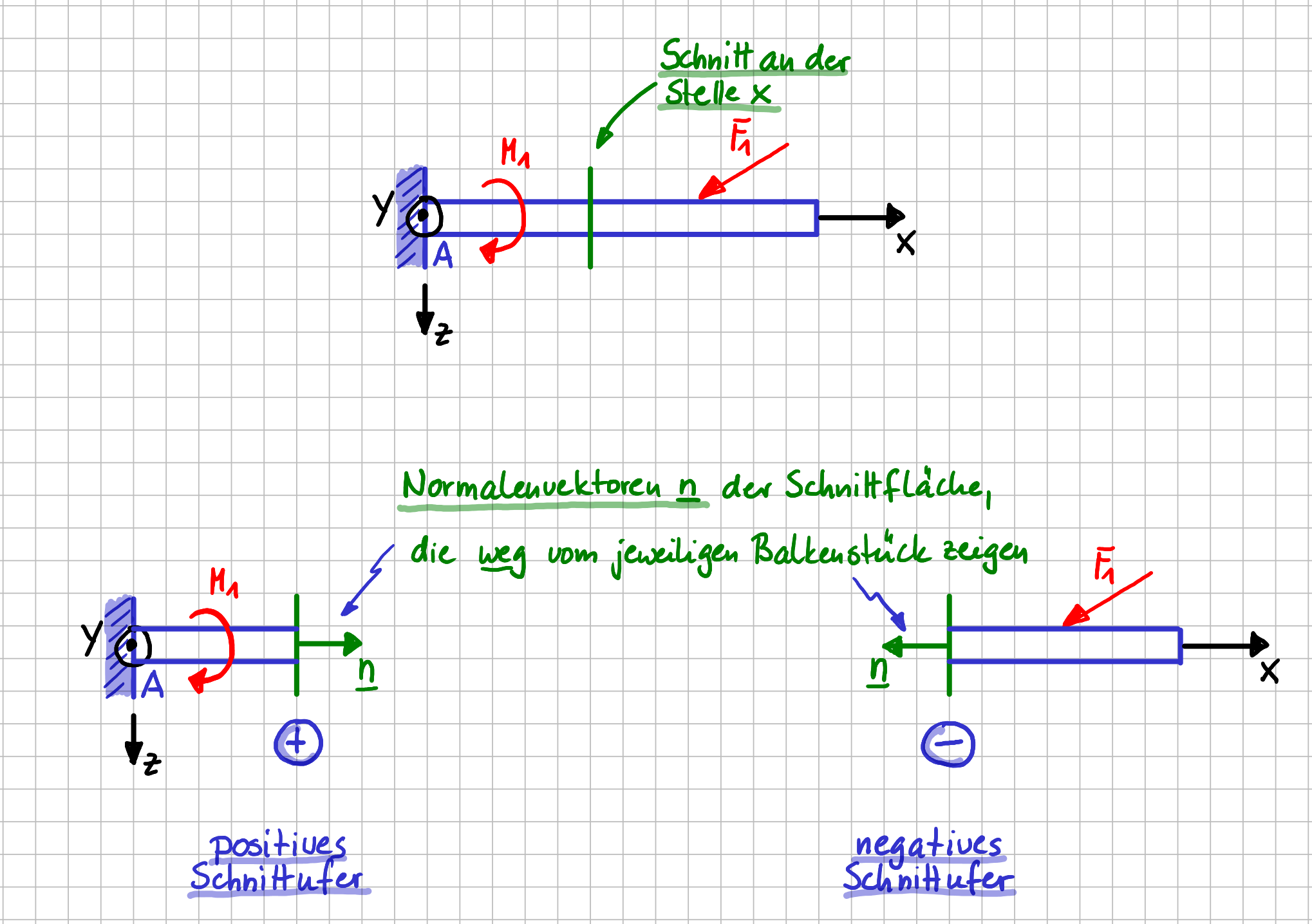
Konvention für die Schnittufer beim Balken
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Konvention_fuer_Schnittufer_beim_Balken.png?time=1735825262175
Zu beiden Schnittflächen gibt es einen Normalenvektor der jeweiligen Schnittfläche, der weg vom zugehörigen Balkenstück zeigt. Dasjenige Schnittufer, bei dem der Normalenvektor in positive \( x \)-Richtung zeigt, wird positives Schnittufer genannt. Das andere Schnittufer, das negative Schnittufer, ist also das Ufer, bei dem der nach außen zeigende Normalenvektor in negative \( x \)-Richtung zeigt.
Zwischenstopp Feste Einspannung
Bevor wir jetzt schauen, was an der Schnittstelle im Balken los ist, möchte ich dich einladen, dich noch einmal kurz daran zu erinnern, was du über das Freischneiden von festen Einspannungen gelernt hast.
Mit einer festen Einspannung ist z.B. ein Balken fest mit der Umgebung verbunden. Es gibt keinerlei Bewegungsmöglichkeit für den Balken relativ zur Umgebung. Alle Freiheitsgrade sind eingeschränkt und es können beliebige Kräfte und Momente übertragen werden. Im ebenen Fall bedeutet das, dass eine resultierende Kraft, die in der \( xz \)-Ebene liegt, und ein Moment um die \( y \)-Achse übertragen werden können. beim Freischneiden der festen Einspannung werden genau diese Reaktionsgrößen sichtbar, wobei die resultierende Kraft typischer Weise gleich in ihre Komponenten in Koordinatenrichtung zerlegt wird.
Als Bezeichnungen wird üblicherweise der Buchstabe verwendet, mit dem der Punkt bezeichnet ist. Und die Größen bekommen je noch einen Index, der ihre Richtung angibt.
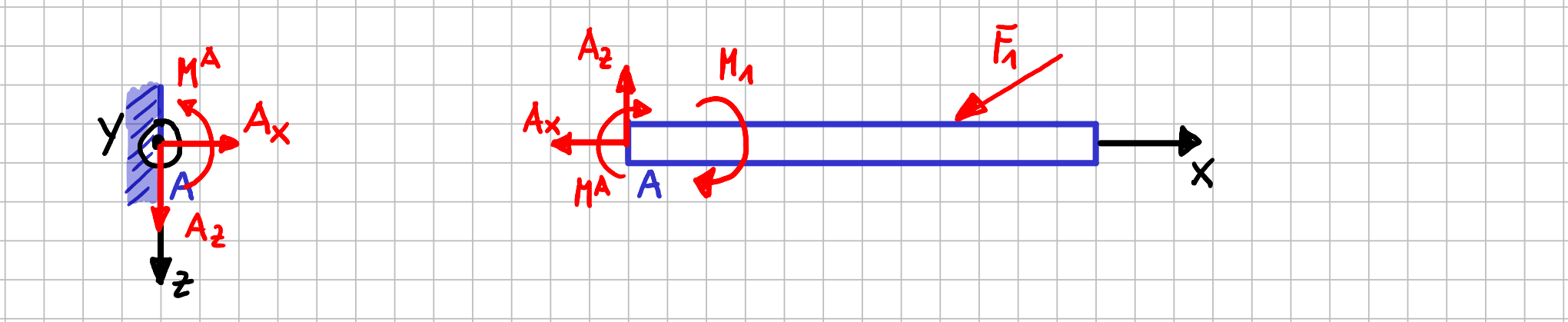
Freikörperbild der festen Einspannung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Freikoerperbild_der_festen_Einspannung.png
Bis vielleicht auf die Wahl der Richtungen des Koordinatensystems sollte dir dieses Vorgehen sehr geläufig sein.
Annäherung an die Schnittgrößen
Was ist denn jetzt eigentlich so anders, wenn du einen Balken irgendwo entlang seiner Länge durchschneidest? Kann sich das Balkenstück rechts vom Schnitt relativ zu dem Stück links vom Schnitt bewegen? Natürlich nicht. Es handelt sich ja um durchgehendes Material. Also sind die beiden Balkenstücke doch von der Lagerart genauso verbunden, wie ein Balken mit der Umgebung bei einer festen Einspannung, oder? Und das bedeutet doch dann nichts anderes, als dass an jeder Stelle entlang des Balkens beliebige Kräfte und Momente übertragen werden können, genauso wie bei der festen Einspannung. Im ebenen Fall, den wir hier ausschließlich betrachten wollen, bedeutet das also wieder eine resultierende Kraft, die in der \( xz \)-Ebene liegt, und ein Moment um die \( y \)-Achse, die übertragen werden können. Wird die resultierende Kraft in ihre Komponenten bezüglich des Koordinatensystems zerlegt, gibt es eine Komponente in \( x \)-Richtung und eine Komponente in \( z \)-Richtung. Es ist also alles genau so, wie bei der festen Einspannung.
Wenn du so willst, ist ein Balken ist also so gesehen eine Aneinanderreihung ganz vieler fester Einspannungen und damit absolut nichts Neues für dich.

Richtungen der positiven Schnittgrößen am positiven Schnittufer
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Richtungen_der_positiven_Schnittgroessen_am_positiven_Schnittufer.png
Vorzeichen für Schnittgrößen
Wir hatten ja schon das positive und das negative Schnittufer eingeführt. Jetzt geht es weiter mit den Konventionen. Man hat sich darauf verständigt, dass am positiven Schnittufer positive Schnittgrößen in positive Koordinatenrichtungen zeigen. Deshalb sind die Schnittgrößen in der vorherigen Abbildung in positive Koordinatenrichtungen eingezeichnet worden.
Wenn du jetzt das negative Schnittufer hinzunimmst, dann solltest du auch sofort wissen, wie du die Schnittgrößen hier einzeichnen musst:
Immer wenn du etwas freischneidest, also zwei Systemteile voneinander trennst, gilt ja das Gegenwirkungsprinzip oder "Actio = Reactio". Also musst du die Schnittgrößen am negativen Schnittufer in negative Koordinatenrichtungen einzeichnen. Sonst sind die Bedingungen für das Gleichgewicht ja nicht mehr erfüllt.
Wenn am positiven Schnittufer positive Schnittgröße in positive Koordinatenrichtungen zeigen, bedeutet das also, dass am negativen Schnittufer positive Schnittgrößen in negative Koordinatenrichtungen zeigen.
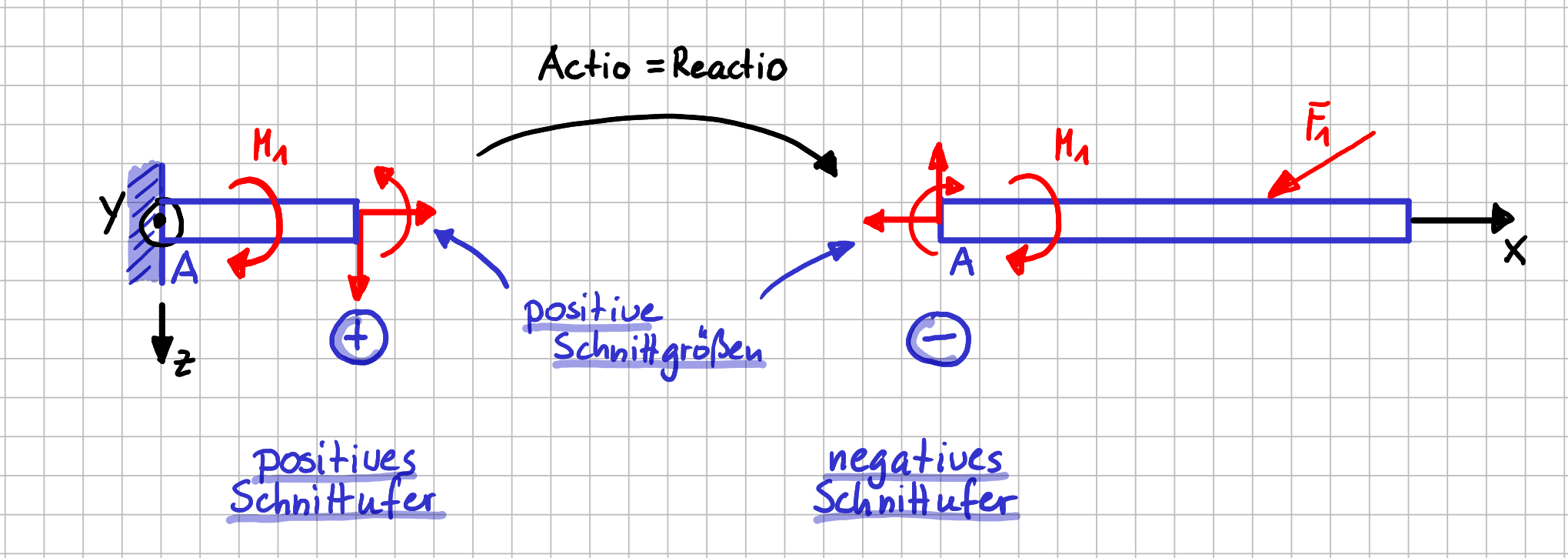
Richtungen der positiven Schnittgrößen an beiden Schnittufern
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Richtungen_der_positiven_Schnittgroessen_an_beiden_Schnittufern.png
Bezeichnungen für Schnittgrößen
Lass uns annehmen, dass der Punkt, an der Schnitt durch den Balken ausgeführt wird, mit \( P \) bezeichnet wird. Nachdem, was du bisher gelernt hast, hättest du die Schnittgrößen am Punkt \( P \) vermutlich so bezeichnet:
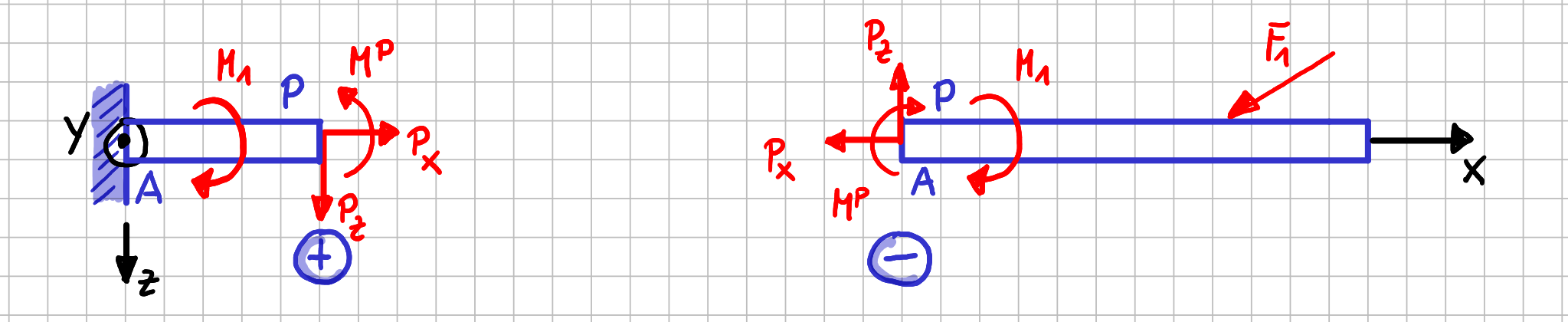
Naheliegende Bezeichnung der Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Naheliegende_Bezeichnung_der_Schnittgroessen.png
Da wir ja schon gesagt haben, dass wir uns für die Verläufe der Schnittgrößen interessieren, also für die Werte der Schnittgrößen an einer beliebigen Stelle \( x \) entlang der \( x \)-Achse, hättest du vermutlich gesagt: "Der Punkt \( P \) kann ja an einer beliebigen Stelle \( x \) innerhalb des Balkens liegen. Also muss gelten \( P_x=P_x(x), P_z=P_z(x) \) und \( M_y^P=M_y^P(x) \), da die Werte der Schnittgrößen ja von der Position des Schnittes abhängen können."
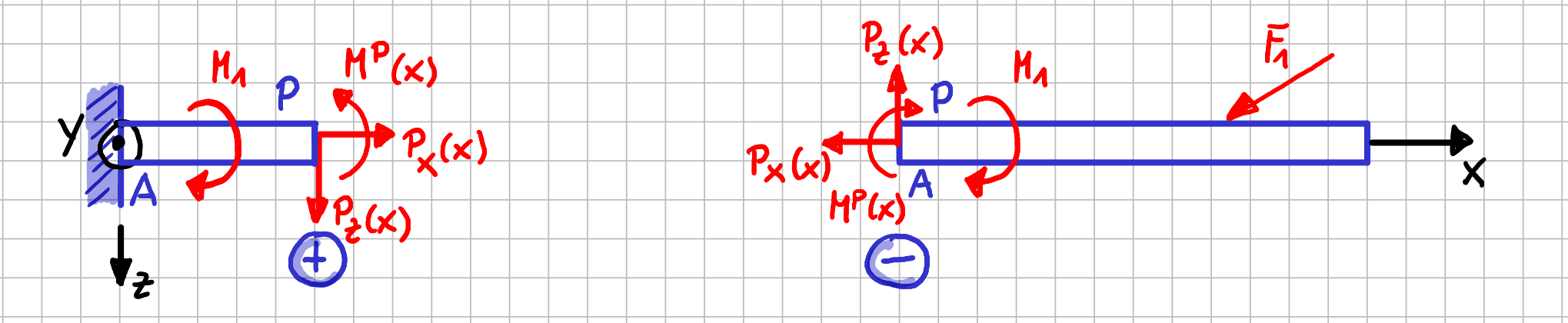
Naheliegende Bezeichnung der Schnittgrößen mit Angabe der Abhängigkeit von der Lage der Schnittes an der Stelle \( x \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Naheliegende_Bezeichnung_der_Schnittgroessen_als_Funktion_von_x.png
Soweit ist alles korrekt und logisch, oder?
Das Einzige, was jetzt noch passiert ist, dass die Schnittgrößen eine andere Bezeichnung bzw. einen anderen Namen bekommen. Das ist wieder so eine Konvention.
\( P_x(x) \) wird mit \( N(x) \) bezeichnet und ist die Normalkraft, weil sie in Richtung des Normalenvektors der Schnittfläche zeigt.
\( P_z(x) \) heißt \( Q(x) \) und ist die Querkraft, weil sie quer zur Balkenachse verläuft.
\( M_y^P(x) \) heißt \( M_{By} \) oder nur \( M_y \) und ist das Biegemoment, weil der Balken, wenn er als verformbar betrachtet würde, sich durch die Wirkung dieses Momentes durchbiegen würde.
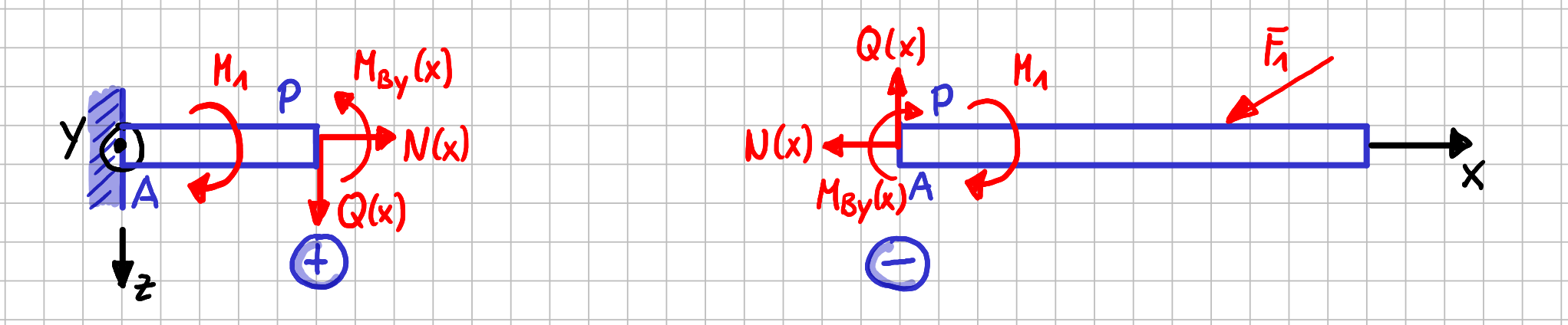
Konvention für die Bezeichnung von Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Konvention_Bezeichnung_Schnittgroessen.png
Das sind sie also, die Schnittgrößen und die zugehörigen Konventionen. Wenn du ehrlich bist, ist bis auf die Konventionen für die Wahl des Koordinatensystems und die Einführung des Begriffs Schnittufer nicht wirklich was neu. Na gut, an die Namen für die Schnittgrößen musst du dich vielleicht noch gewöhnen. Aber ansonsten gilt: Wenn du eine feste Einspannung freischneiden kannst und das Prinzip "Actio = Reactio" beherrschst, kennst du schon alle wesentlichen mechanischen Inhalte, die du bis hierher benötigt hast.
