Schnittgrößen
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Schnittgrößen |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 12:48 |
1. Einstieg Schnittgrößen
Einstieg Schnittgrößen
Tragwerke, die aus einem oder
mehreren Balken bestehen, kommen im Ingenieurwesen häufig vor.
Es ist
daher wichtig, die Verteilung der Belastungen im Inneren eines Balkens
-sie werden als Schnittgrößen bezeichnet- berechnen zu können.
Schließlich müssen Material und Querschnitt eines Balkens so gewählt
werden, dass der Balken unter allen auftretenden Lastszenarien sicher
hält und nicht versagt. Gleichzeitig darf die Konstruktion nicht
hoffnungslos überdimensioniert sein, weil sie dann viel zu teuer und unnötig schwer wäre.
In dieser Lektion wollen wir uns
dem Thema Schnittgrößen in mehreren Schritten nähern.
Zuerst werden wir uns anschauen, was Schnittgrößen nun wirklich
genau sind.
Dann schauen wir, wie du die Verläufe von Schnittgrößen entlang der Länge eines Balkens mit dem Handwerkszeug berechnen kannst, das du inzwischen schon sehr gut kennst: Freischneiden, Gleichgewichtsbedingungen aufstellen und auswerten. Hiermit legst du die Grundlagen für alles, was mit dem mechanisch Verständnis des Themas Schnittgrößen zu tun hat. Es ist also sehr wichtig, dass du hierbei ganz besonders gründlich vorgehst und die Zusammenhänge wirklich verstehst.
Danach betrachten wir, welche Zusammenhänge zwischen den Belastungen und den Schnittgrößen bestehen und wie du diese Zusammenhänge für die Berechnung der Verläufe der Schnittgrößen über die Länge des Balkens verwenden kannst. Du wirst sehen, dass die mathematische Beschreibung in diesem Schritt schon deutlich eleganter wird.
2. Was sind Schnittgrößen?
Was sind Schnittgrößen?
Wird ein Balken von außen belastet, treten in seinem Inneren Kräfte und Momente auf. Es ist wichtig, diese inneren Größen berechnen zu können. Nur so kann die Tragfähigkeit von Tragwerken untersucht oder zum Beispiel der erforderliche Querschnitt eines Balkens festgelegt, also dimensioniert werden.
Wie Reaktionsgrößen bei Lagern werden innere Kräfte und Momente durch Freischneiden sichtbar. Deswegen werden diese Größen zusammen auch als Schnittgrößen bezeichnet.
Der Wert der Schnittgrößen ist in der Regel davon abhängig, an welcher Stelle entlang seiner Länge der Balken geschnitten wird.
Konvention für das Koordinatensystem
Bevor wir den ersten Balken durchschneiden, um das sichtbar machen zu können, was in seinem Inneren passiert, lohnt es sich, dass wir uns erstmal auf ein paar Konventionen einigen. Die erste Konvention betrifft die Wahl des Koordinatensystems. Bei Balken hat man sich auf Folgendes verständigt:
1. Der Ursprung des Koordinatensystems liegt an einem Ende des Balkens.
2. Die \( x \)-Achse zeigt läuft entlang der Balkenachse, so dass \( x \) nur den Wert Null oder positive Werte haben kann.
3. Die \( z \)-Achse zeigt senkrecht dazu "nach unten" und liegt in der Bildebene.
4. Die \( y \)-Achse zeigt demnach gemäß der Rechte-Hand-Regel für Koordinatensysteme aus der Bildebene heraus.
Konvention für das Koordinatensystem beim Balken
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Konvention_KOS_Balken.png
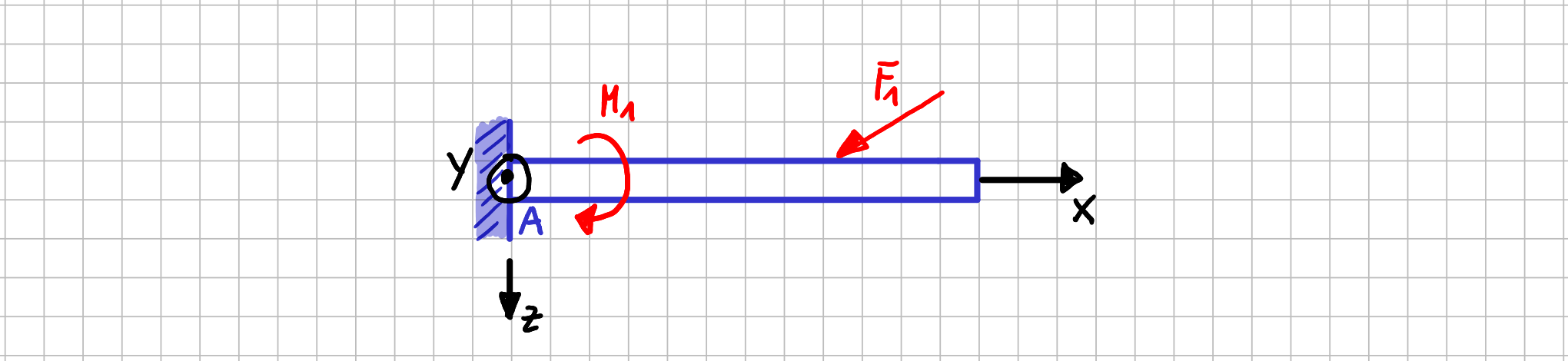
Konvention für die Schnittufer
Wird ein Balken an einer beliebigen Stelle entlang seiner Länge senkrecht zu seiner Hauptrichtung geschnitten, entstehen zwei Teilsysteme.
Im folgenden Beispiel gibt es ein linkes und ein rechtes Teilsystem.
Konvention für die Schnittufer beim Balken
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Konvention_fuer_Schnittufer_beim_Balken.png?time=1735825262175
Zu beiden Schnittflächen gibt es einen Normalenvektor der jeweiligen Schnittfläche, der weg vom zugehörigen Balkenstück zeigt. Dasjenige Schnittufer, bei dem der Normalenvektor in positive \( x \)-Richtung zeigt, wird positives Schnittufer genannt. Das andere Schnittufer, das negative Schnittufer, ist also das Ufer, bei dem der nach außen zeigende Normalenvektor in negative \( x \)-Richtung zeigt.
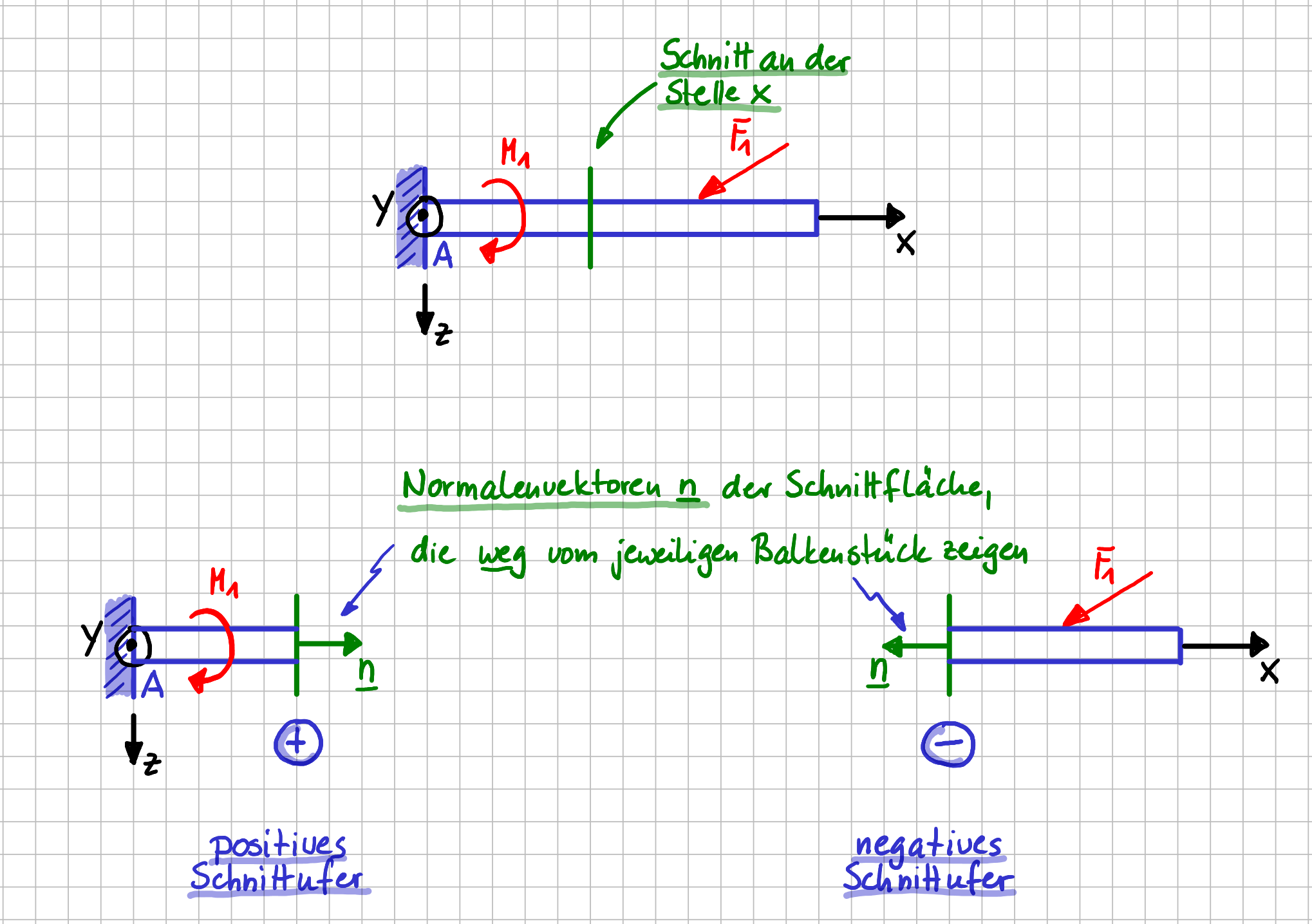
Zwischenstopp Feste Einspannung
Bevor wir jetzt schauen, was an der Schnittstelle im Balken los ist, möchte ich dich einladen, dich noch einmal kurz daran zu erinnern, was du über das Freischneiden von festen Einspannungen gelernt hast.
Mit einer festen Einspannung ist z.B. ein Balken fest mit der Umgebung verbunden. Es gibt keinerlei Bewegungsmöglichkeit für den Balken relativ zur Umgebung. Alle Freiheitsgrade sind eingeschränkt und es können beliebige Kräfte und Momente übertragen werden. Im ebenen Fall bedeutet das, dass eine resultierende Kraft, die in der \( xz \)-Ebene liegt, und ein Moment um die \( y \)-Achse übertragen werden können. beim Freischneiden der festen Einspannung werden genau diese Reaktionsgrößen sichtbar, wobei die resultierende Kraft typischer Weise gleich in ihre Komponenten in Koordinatenrichtung zerlegt wird.
Als Bezeichnungen wird üblicherweise der Buchstabe verwendet, mit dem der Punkt bezeichnet ist. Und die Größen bekommen je noch einen Index, der ihre Richtung angibt.
Freikörperbild der festen Einspannung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Freikoerperbild_der_festen_Einspannung.png
Bis vielleicht auf die Wahl der Richtungen des Koordinatensystems sollte dir dieses Vorgehen sehr geläufig sein.
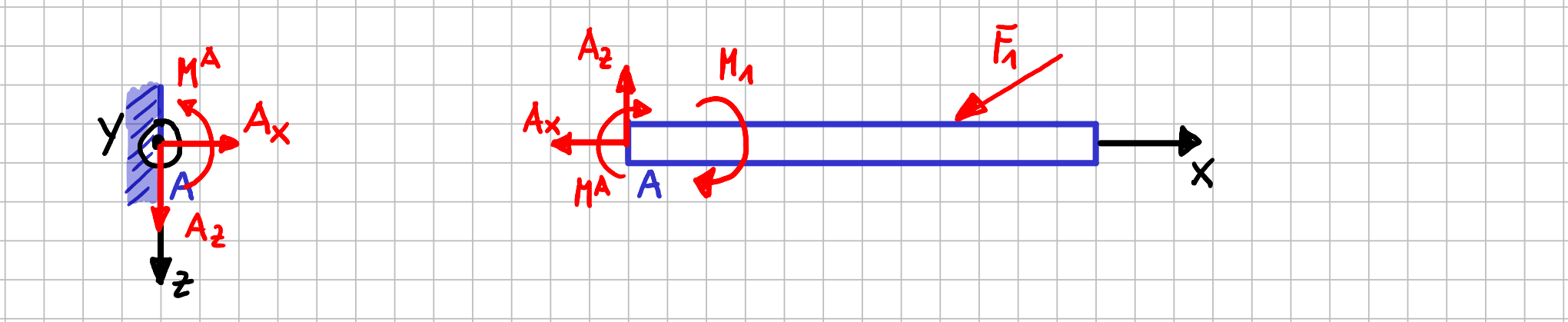
Annäherung an die Schnittgrößen
Was ist denn jetzt eigentlich so anders, wenn du einen Balken irgendwo entlang seiner Länge durchschneidest? Kann sich das Balkenstück rechts vom Schnitt relativ zu dem Stück links vom Schnitt bewegen? Natürlich nicht. Es handelt sich ja um durchgehendes Material. Also sind die beiden Balkenstücke doch von der Lagerart genauso verbunden, wie ein Balken mit der Umgebung bei einer festen Einspannung, oder? Und das bedeutet doch dann nichts anderes, als dass an jeder Stelle entlang des Balkens beliebige Kräfte und Momente übertragen werden können, genauso wie bei der festen Einspannung. Im ebenen Fall, den wir hier ausschließlich betrachten wollen, bedeutet das also wieder eine resultierende Kraft, die in der \( xz \)-Ebene liegt, und ein Moment um die \( y \)-Achse, die übertragen werden können. Wird die resultierende Kraft in ihre Komponenten bezüglich des Koordinatensystems zerlegt, gibt es eine Komponente in \( x \)-Richtung und eine Komponente in \( z \)-Richtung. Es ist also alles genau so, wie bei der festen Einspannung.
Wenn du so willst, ist ein Balken ist also so gesehen eine Aneinanderreihung ganz vieler fester Einspannungen und damit absolut nichts Neues für dich.

Richtungen der positiven Schnittgrößen am positiven Schnittufer
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Richtungen_der_positiven_Schnittgroessen_am_positiven_Schnittufer.png
Vorzeichen für Schnittgrößen
Wir hatten ja schon das positive und das negative Schnittufer eingeführt. Jetzt geht es weiter mit den Konventionen. Man hat sich darauf verständigt, dass am positiven Schnittufer positive Schnittgrößen in positive Koordinatenrichtungen zeigen. Deshalb sind die Schnittgrößen in der vorherigen Abbildung in positive Koordinatenrichtungen eingezeichnet worden.
Wenn du jetzt das negative Schnittufer hinzunimmst, dann solltest du auch sofort wissen, wie du die Schnittgrößen hier einzeichnen musst:
Immer wenn du etwas freischneidest, also zwei Systemteile voneinander trennst, gilt ja das Gegenwirkungsprinzip oder "Actio = Reactio". Also musst du die Schnittgrößen am negativen Schnittufer in negative Koordinatenrichtungen einzeichnen. Sonst sind die Bedingungen für das Gleichgewicht ja nicht mehr erfüllt.
Wenn am positiven Schnittufer positive Schnittgröße in positive Koordinatenrichtungen zeigen, bedeutet das also, dass am negativen Schnittufer positive Schnittgrößen in negative Koordinatenrichtungen zeigen.
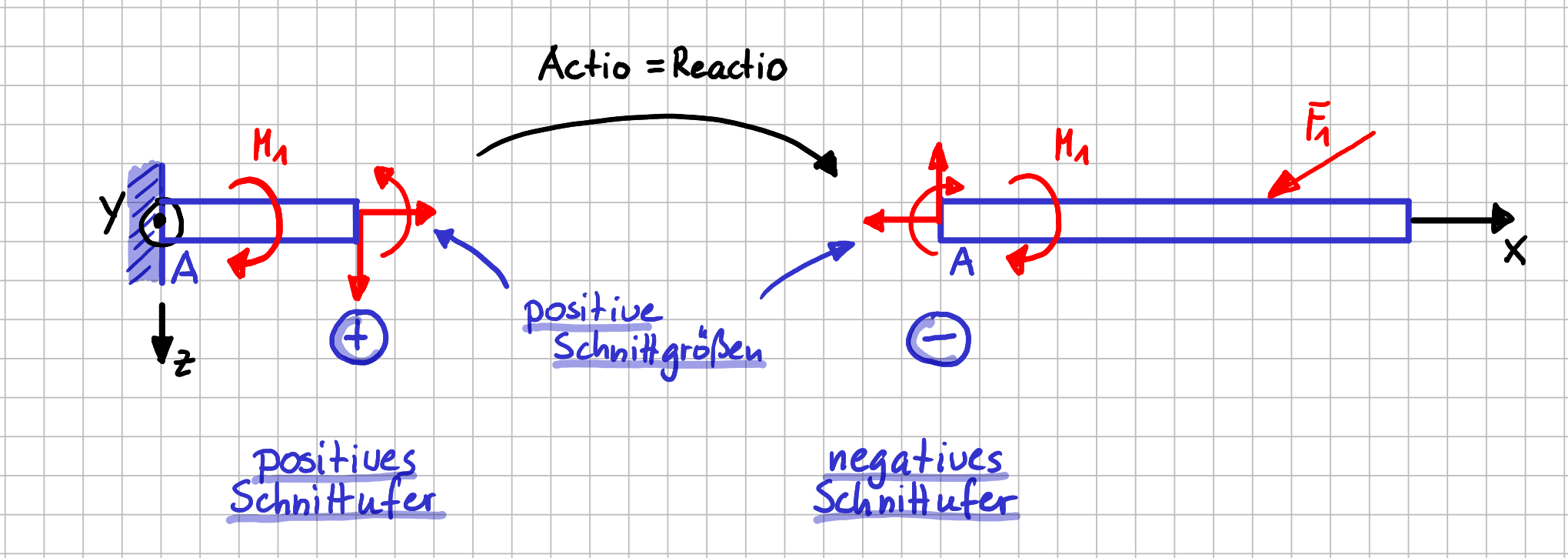
Richtungen der positiven Schnittgrößen an beiden Schnittufern
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Richtungen_der_positiven_Schnittgroessen_an_beiden_Schnittufern.png
Bezeichnungen für Schnittgrößen
Lass uns annehmen, dass der Punkt, an der Schnitt durch den Balken ausgeführt wird, mit \( P \) bezeichnet wird. Nachdem, was du bisher gelernt hast, hättest du die Schnittgrößen am Punkt \( P \) vermutlich so bezeichnet:
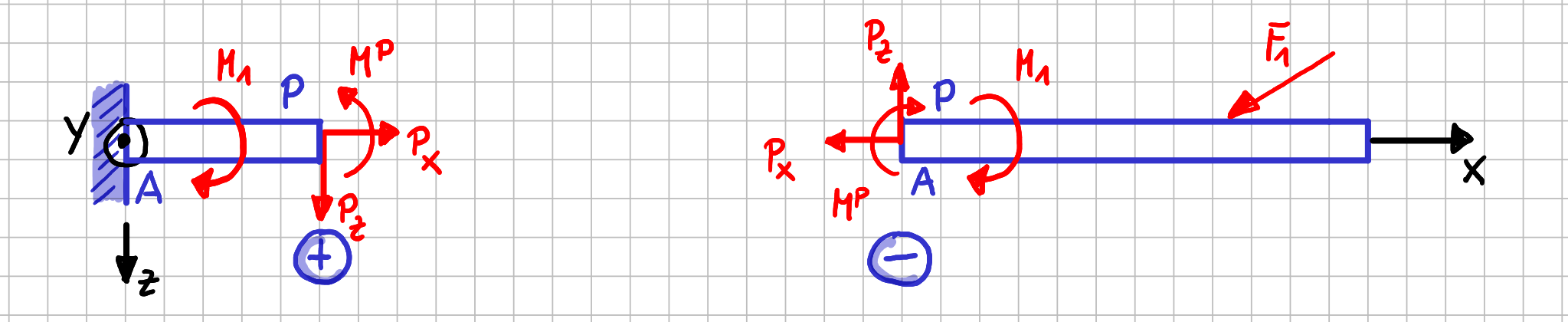
Naheliegende Bezeichnung der Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Naheliegende_Bezeichnung_der_Schnittgroessen.png
Da wir ja schon gesagt haben, dass wir uns für die Verläufe der Schnittgrößen interessieren, also für die Werte der Schnittgrößen an einer beliebigen Stelle \( x \) entlang der \( x \)-Achse, hättest du vermutlich gesagt: "Der Punkt \( P \) kann ja an einer beliebigen Stelle \( x \) innerhalb des Balkens liegen. Also muss gelten \( P_x=P_x(x), P_z=P_z(x) \) und \( M_y^P=M_y^P(x) \), da die Werte der Schnittgrößen ja von der Position des Schnittes abhängen können."
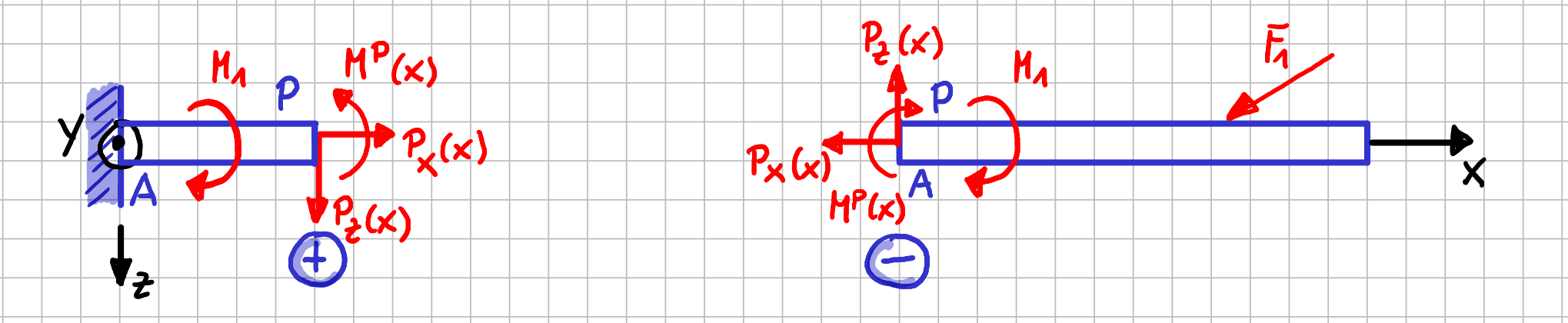
Naheliegende Bezeichnung der Schnittgrößen mit Angabe der Abhängigkeit von der Lage der Schnittes an der Stelle \( x \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Naheliegende_Bezeichnung_der_Schnittgroessen_als_Funktion_von_x.png
Soweit ist alles korrekt und logisch, oder?
Das Einzige, was jetzt noch passiert ist, dass die Schnittgrößen eine andere Bezeichnung bzw. einen anderen Namen bekommen. Das ist wieder so eine Konvention.
\( P_x(x) \) wird mit \( N(x) \) bezeichnet und ist die Normalkraft, weil sie in Richtung des Normalenvektors der Schnittfläche zeigt.
\( P_z(x) \) heißt \( Q(x) \) und ist die Querkraft, weil sie quer zur Balkenachse verläuft.
\( M_y^P(x) \) heißt \( M_{By} \) oder nur \( M_y \) und ist das Biegemoment, weil der Balken, wenn er als verformbar betrachtet würde, sich durch die Wirkung dieses Momentes durchbiegen würde.
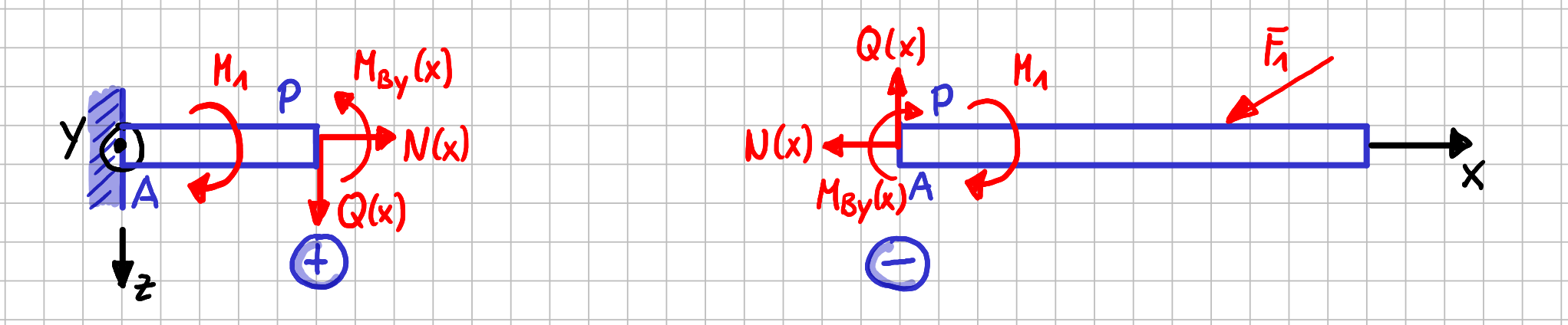
Konvention für die Bezeichnung von Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2220/Konvention_Bezeichnung_Schnittgroessen.png
Das sind sie also, die Schnittgrößen und die zugehörigen Konventionen. Wenn du ehrlich bist, ist bis auf die Konventionen für die Wahl des Koordinatensystems und die Einführung des Begriffs Schnittufer nicht wirklich was neu. Na gut, an die Namen für die Schnittgrößen musst du dich vielleicht noch gewöhnen. Aber ansonsten gilt: Wenn du eine feste Einspannung freischneiden kannst und das Prinzip "Actio = Reactio" beherrschst, kennst du schon alle wesentlichen mechanischen Inhalte, die du bis hierher benötigt hast.
Arbeitsblatt - Teste dein Wissen
3. Berechnung mittels Aufstellen von Gleichgewichtsbedigungen
Berechnung mittels Aufstellen von Gleichgewichtsbedigungen
Wie lassen sich Schnittgrößen denn nun berechnen?
Naja, wie du gesehen hast, war ja beim Einführen schon viel Bekanntes dabei. Dann besteht doch die Hoffnung, dass das bei der Berechnung der Schnittgrößen auch so ist, oder? Und genauso ist es.
Wir wollen uns das generelle Vorgehen an einem ganz einfachen System anschauen: Einem Balken der Länge \( 2 a \) mit Fest-Los-Lagerung und einer Einzelkraft senkrecht zur Balkenachse in der Mitte und einer Einzelkraft in Balkenrichtung am rechten Ende.
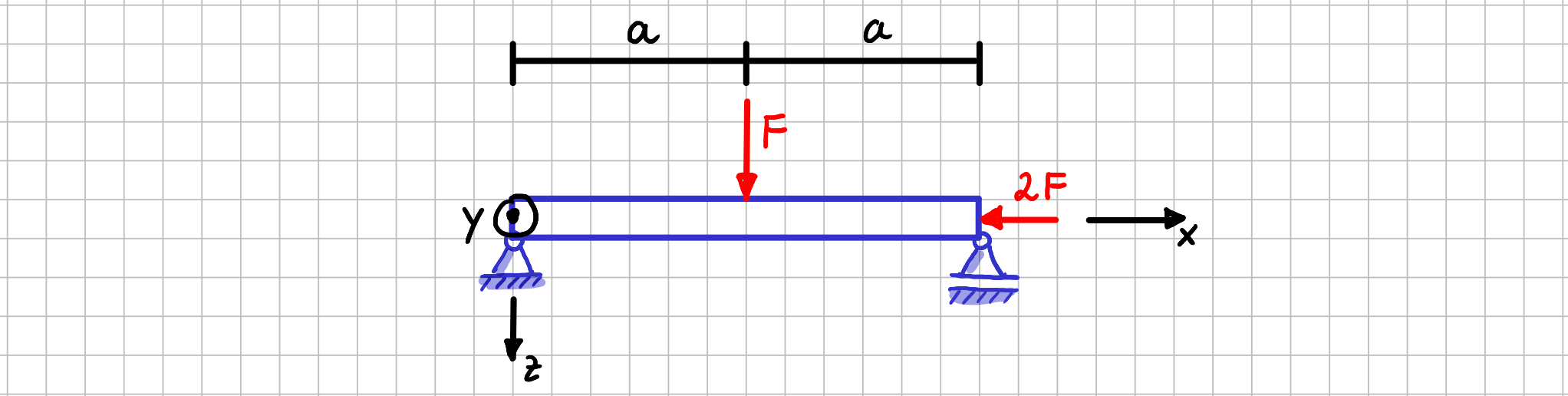
Einfaches System für den Einstieg in die Berechnung von Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Einfaches_System_Berechnung_Schnittgroessen.png
Wenn du im ersten Schritt die Lager freischneidest, ein Freikörperbild aufzeichnest und die Lagerreaktionen bestimmst, bekommst du das folgende Ergebnis.
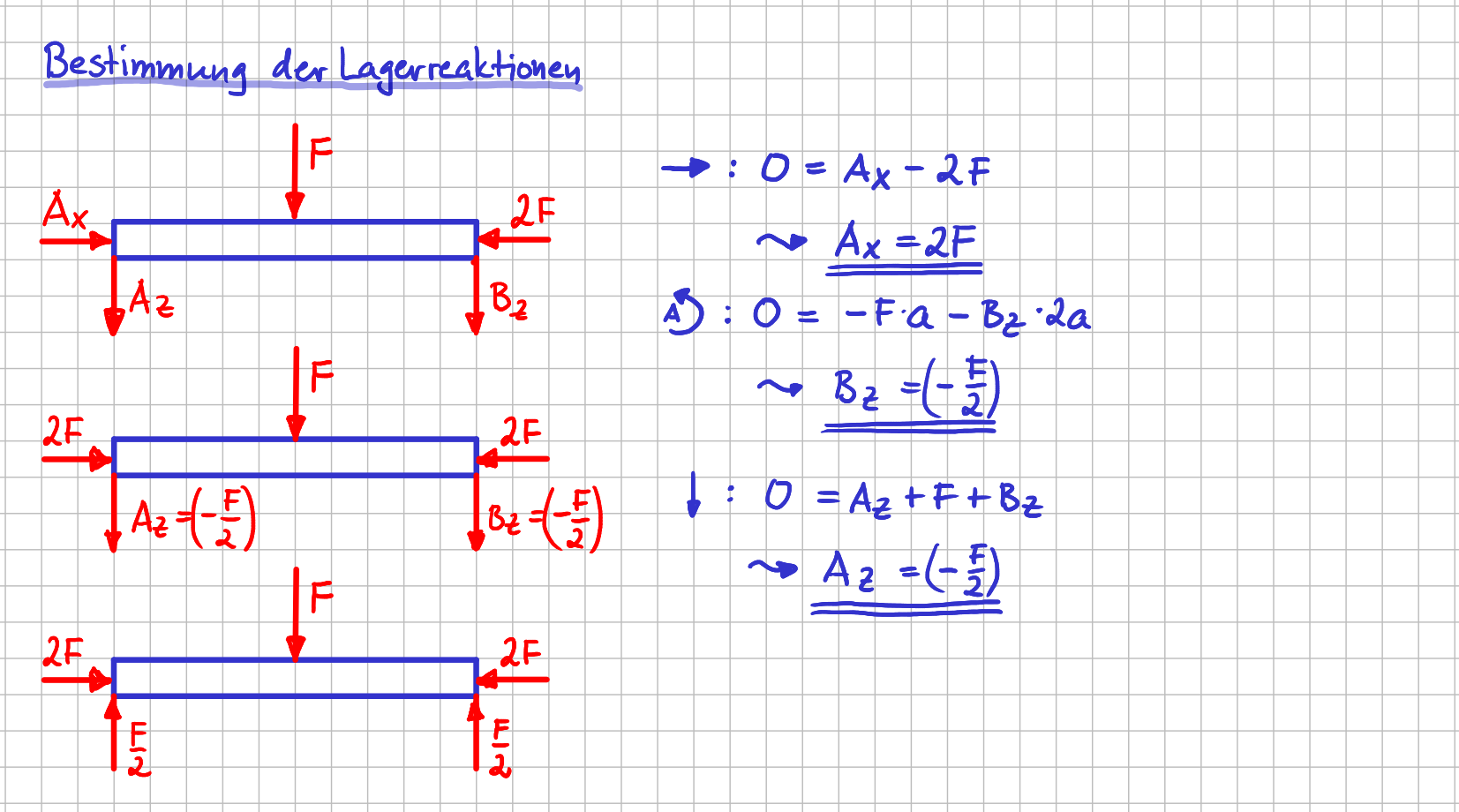
Bestimmung der Lagerreaktionen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Bestimmung_der_Lagerreaktionen.png
Vielleicht musst du für dieses einfache System inzwischen auch schon gar nicht mehr rechnen, sondern 'siehst' das Ergebnis sofort.
So, jetzt aber: Nun wollen wir ins Innere des Balkens hineinschauen und die Funktionen für die Schnittgrößen bestimmen und ihre Verläufe zeichnen.
Wenn wir den Balken irgendwo im Bereich \( 0 < x < a \) durchschneiden, sehen die Freikörperbilder der beiden Teilsysteme so aus:
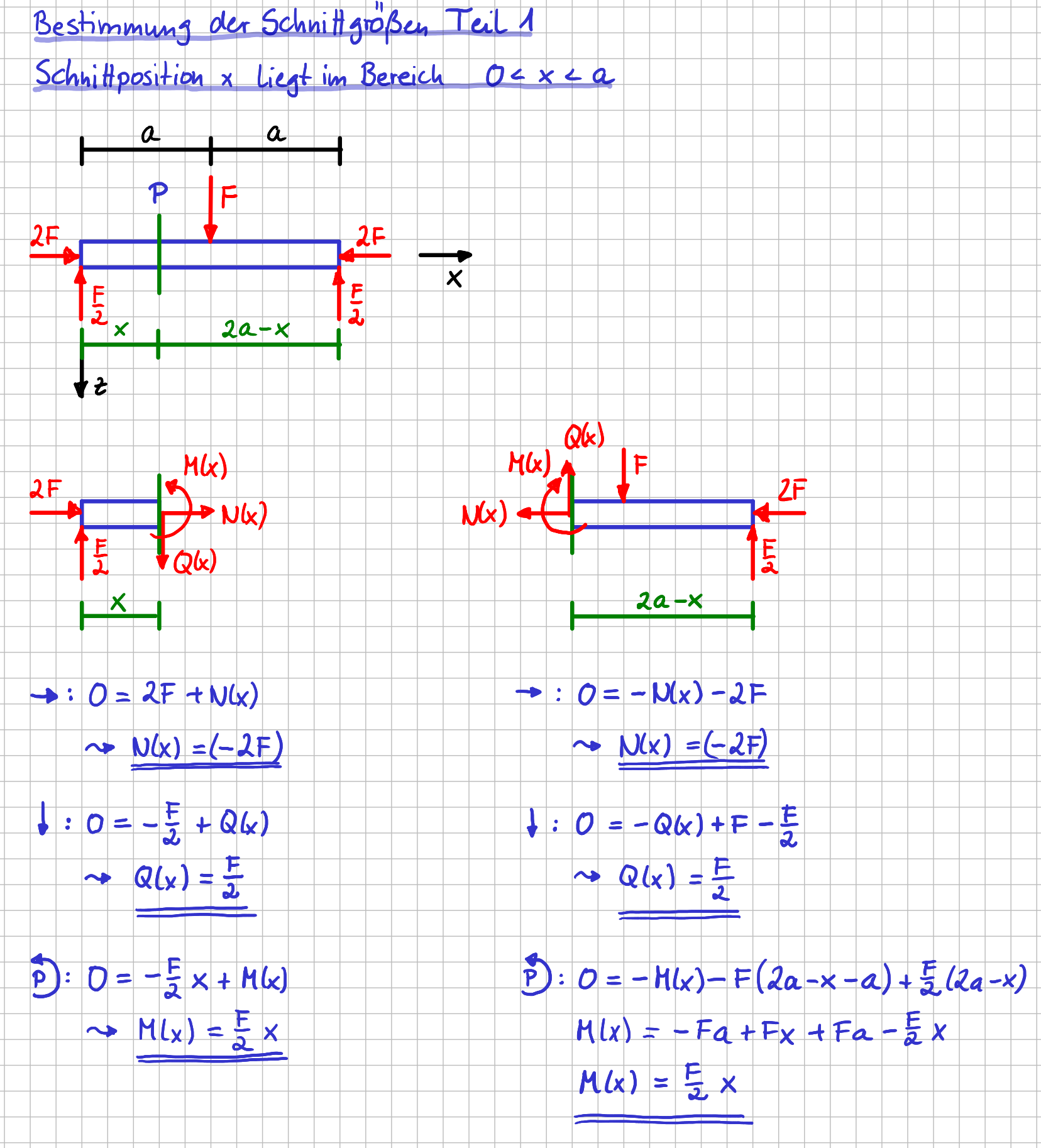
Schnitt mit Schnittposition \( x \) im Bereich \( 0 < x < a \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Schnitt_mit_Schnittposition_1.png
Wenn du die Gleichgewichtsbedingungen aufstellst siehst du, dass du in diesem Beispiel jeweils eine Gleichung direkt nach einer der gesuchten Schnittgrößen \( N \) , \( Q \) und \( M \) auflösen kannst. Dabei ist es egal, ob du die Gleichungen für das linke oder das rechte Teilsystem aufstellst. Das wiederum ist ja völlig logisch, da in der Statik auch jedes herausgeschnittene Teilsystem wieder im Gleichgewicht ist, wenn an der Schnittstelle geeignete Reaktionsgrößen berücksichtigt werden und genau das haben wir ja getan.
An der Stelle \( x=a \) passiert etwas im System: dort greift die Kraft \( F \) an. Das bedeutet, dass sich die Qualität des Freikörperbilds ändert. Daher musst du in einem zweiten Schritt betrachten, was passiert, wenn der Schnitt im Bereich \( a < x < 2a \) liegt.
Achtung: Dieser Bereich gibt nur die Lage der Schnittposition an. Die beiden sich ergebenden Teilsysteme des Balkens haben natürlich trotzdem ihre volle Länge.
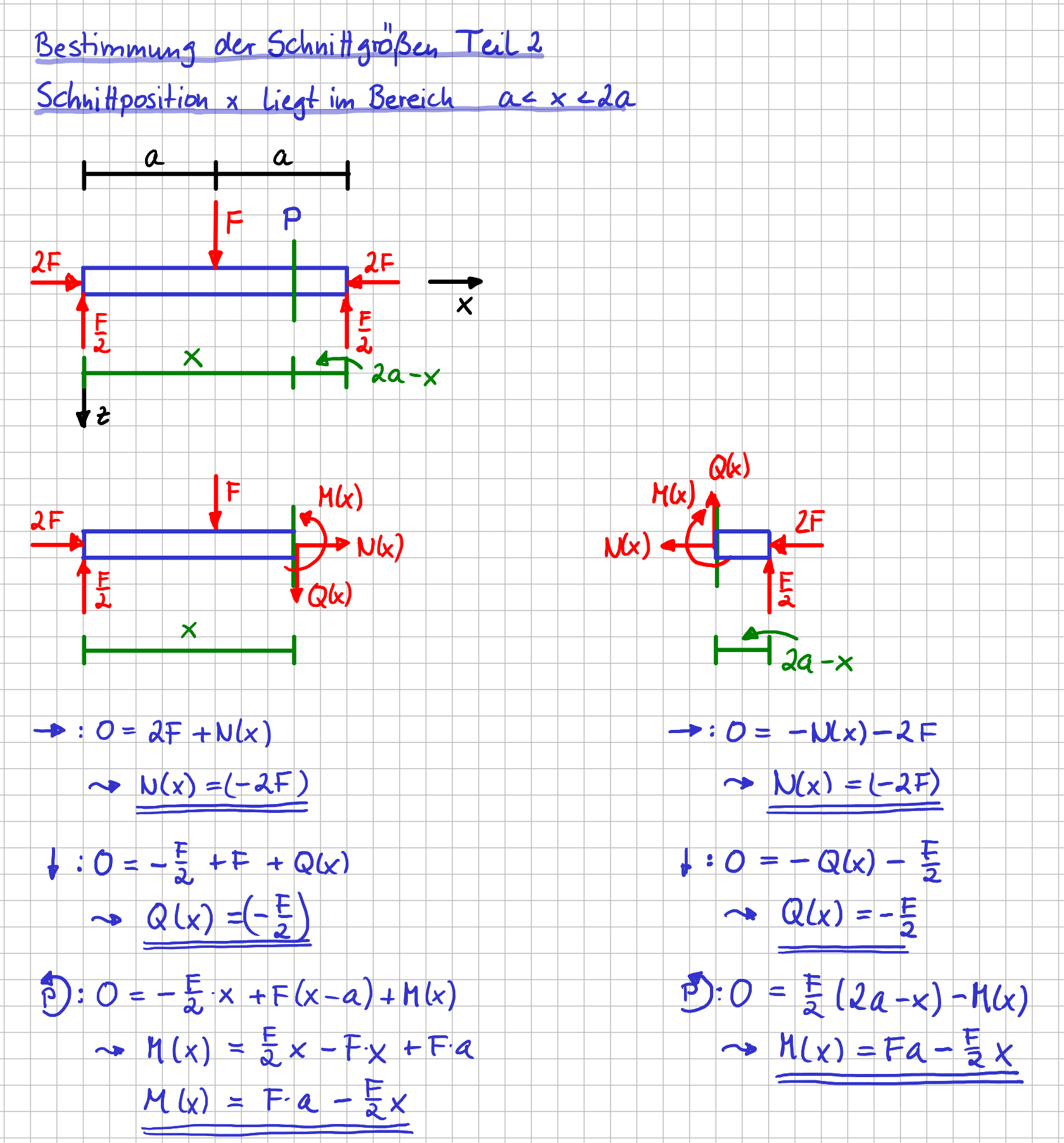
Schnitt mit Schnittposition \( x \) im Bereich \( a < x < 2a \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Schnitt_mit_Schnittposition_2.png
Wenn du wieder die Gleichgewichtsbedingungen aufstellst und auswertest, kannst du wieder direkt nach den gesuchten Schnittgrößen auflösen.
Du hast also für die beiden unterschiedlichen Bereiche, in denen sich die Schnittposition \( x \) bewegen kann, ohne dass sich die Qualität der Freikörperbilder der Teilsysteme ändert, Funktionen für die drei Schnittgrößen Normalkraft \( N(x) \), Querkraft \( Q(x) \) und Biegemoment \( M(x) \) bekommen.
Diese Verläufe kannst du in Diagramme zeichnen. Das sieht dann so aus.
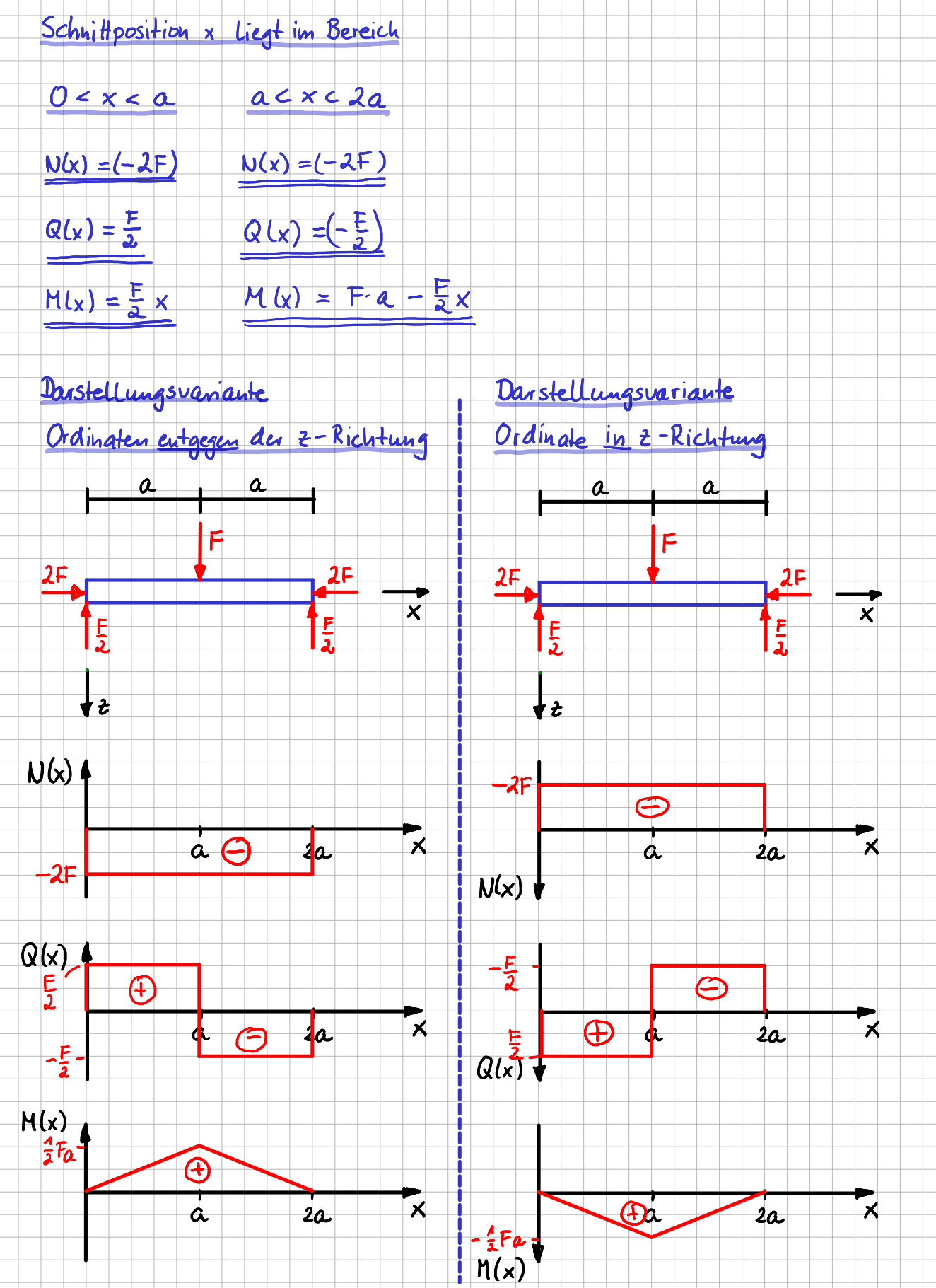
Darstellung der Verläufe der Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Darstellung_der_Verlaeufe.png
Es gibt verschiedene Arten, wie du die Verläufe darstellen kannst. Einige Berufszweige und damit auch Lehrbücher befürworten es, die Ordinate der Diagramme 'nach oben' also entgegen der positiven \( z \)-Richtung einzuzeichnen. Andere zeichnen die Achsen 'nach unten' also in positive \( z \)- Richtung ein. Auch eine Mischform kommt vor.
Deswegen habe ich dir in der vorherigen Abbildung zwei verschiedene Varianten aufgezeichnet.
Was auch ohne Zeichnen der Verläufe schon klar war: die Werte der Normalkraft sind vollständig entkoppelt von dem, was in \( z \)-Richtung los ist, also vom Querkraft- und Momentenverlauf. Beim Querkraft- und Momentenverlauf hingegen kannst du vielleicht schon einen Zusammenhang erkennen, oder? Wenn du dir den Momentenverlauf anschaust und mal die Steigung der gezeigten Kurve betrachtest: Was fällt dir auf?
Genau, die Steigung des Momentenverlaufs entspricht gerade dem Wert der Querkraft an der entsprechenden Stelle. Genau auf diese Art der Zusammenhänge und die sich daraus ergebenden Konsequenzen für die Berechnung von Schnittgrößen gehen wir im nächsten Abschnitt weiter ein.
Bleibt noch die Frage: Und wie ist das Vorgehen bei der abschnittsweisen Betrachtung, wenn eine Streckenlast vorhanden ist? Eigentlich gehst du nicht wirklich anders mit einer Streckenlast um, als du es tust, wenn du die Lagerreaktionen für das Gesamtsystem bestimmst. Dort fasst du die Streckenlast ja zu einer resultierenden Einzelkraft zusammen.
Ich habe hier nochmal ein Beispiel mit einer dreiecksförmigen Streckenlast für dich. Wenn du nochmal Schritt für Schritt sehen möchtest, wie du die resultierende Einzelkraft bestimmst, schau gerne in der Lektion Grundgrößen \( \rightarrow \) Kraft \( \rightarrow \) Verschiedene Kräfte ganz nah \( \rightarrow \) Streckenlast nach.
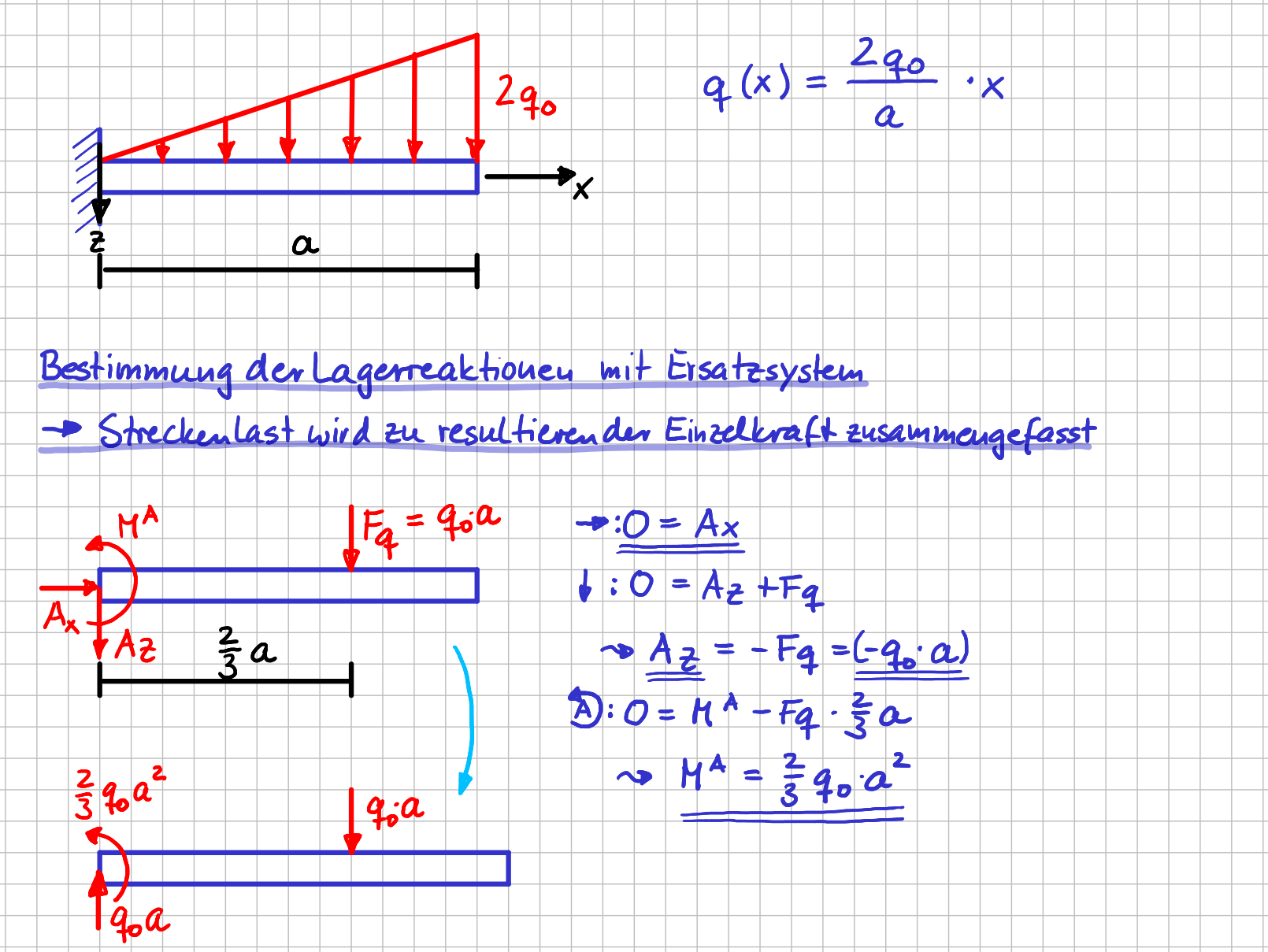
Bestimmung der Lagerreaktionen bei einem Balken mit dreiecksförmiger Streckenlast
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Bestimmung_Lagerreaktionen_dreiecksfoermige_Streckenlast.png
Wenn du jetzt für dieses System die Schnittgrößen bestimmen willst, gehst du ganz ähnlich vor. Allerdings bestimmst du jetzt die resultierende Einzelkraft für das Teil(!)system rechts oder links vom Schnitt. Du führst also als erstes den Schnitt ein und zeichnest ein Freikörperbild des Teilsystems, mit dem du weiter arbeiten möchtest. Für dieses Teilsystem bildest du dann die resultierende Einzelkraft für den Streckenlastanteil, der eben in diesem Teilsystem vorhanden ist.
Wie das konkret geht, siehst du in der folgenden Abbildung.
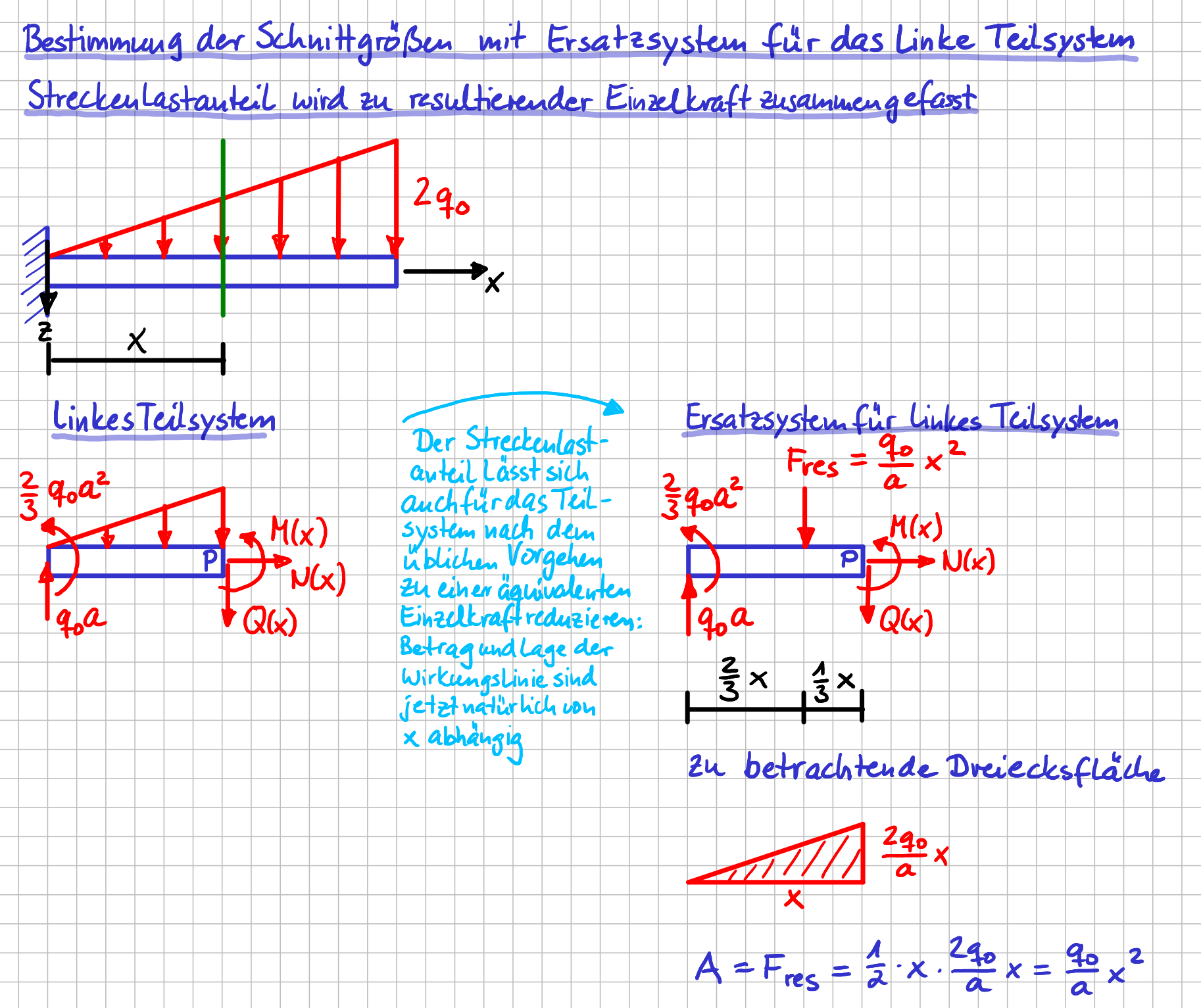
Auf dem Weg zu den Schnittgrößen: Bestimmung der resultierenden Einzelkraft für das linke Teilsystem
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Auf_dem_Weg_zu_den_Schnittgroessen_Einzellast.png
Und für das Ersatzsystem des linken Teilsystems kannst du jetzt wieder 'wie immer' die Gleichgewichtsbedingungen aufstellen und diese dann nach den Schnittgrößen umstellen.
Das sieht dann so aus:
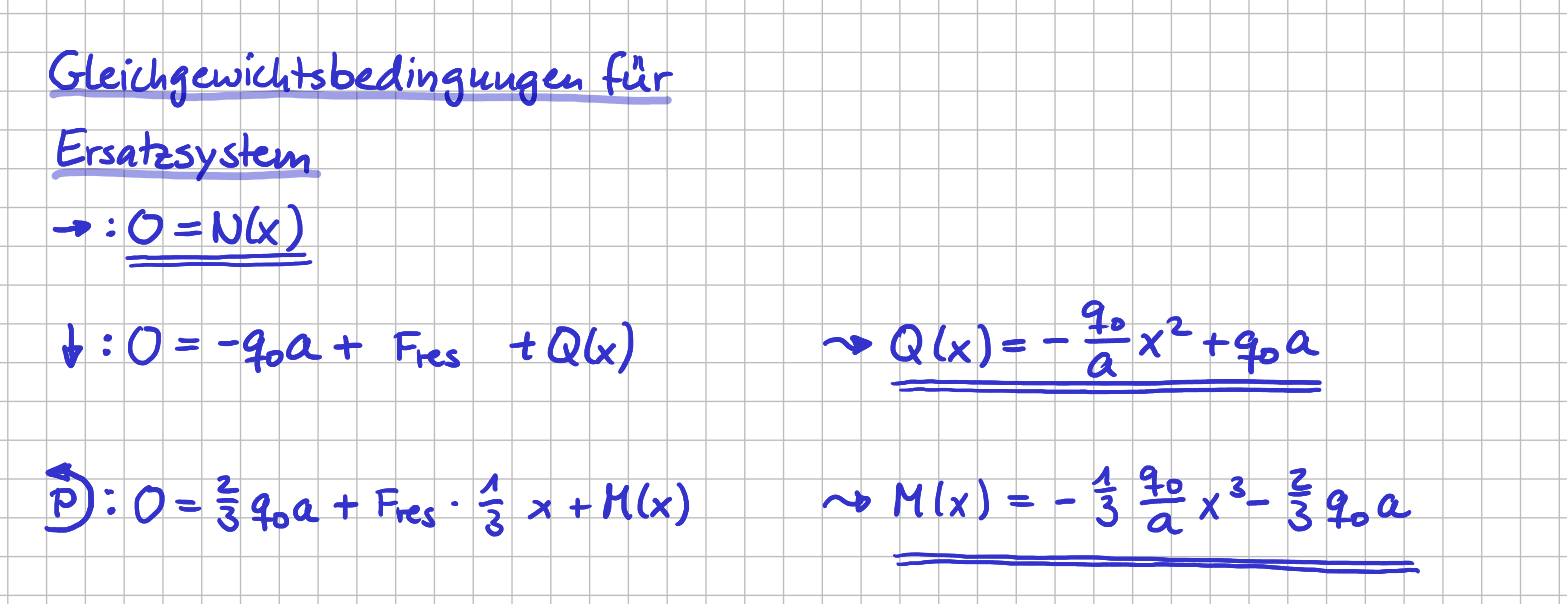
Bestimmung der Schnittgrößen aus den Gleichgewichtsbedingungen des Ersatzsystems
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Bestimmung_der_Schnittgroessen_aus_Ersatzsystem.png
Wenn du dich fragst, warum Schnittgrößen überhaupt ausgerechnet werden? Stell dir vor du hast einen Balken in einem realen System. Der ist irgendwann mal für gewisse Lastfälle ausgelegt worden. Sein Material und seine geometrischen Abmessungen sind also unter der Annahme bestimmter äußerer Belastungen festgelegt worden. Jetzt kommt ein neuer Lastfall hinzu und du möchtest feststellen, ob der Balken immer noch halten würde. Dazu musst du natürlich erstmal wissen, an welcher Stelle die kritischen inneren Größen auftreten. Es gibt Werkstoffe, die besonders empfindlich bei Zugbelastungen sind. Andere Werkstoffe versagen typischer Weise aufgrund von Scherbelastungen, wie sie durch Querkräfte erzeugt werden. Die Bestimmung von Schnittgrößen hat also große praktische Bedeutung. Wie du genau feststellen kannst, ob ein Balken hält oder nicht, lernst du in dem Teilgebiet der Mechanik, dass sich Elastostatik nennt. Hier werden die sich aus den Schnittgrößen ergebenden Spannungen betrachtet und die zugehörigen Deformationen betrachtet.
4. Berechnung mittels Integration / Ableitung
Berechnung mittels Integration / Ableitung
Wenn du die Inhalte des vorangegangenen Abschnitts gut durchgearbeitet und verinnerlicht hast, ist es an der Zeit, einen Schritt weiterzugehen.
Zwischen dem Verlauf \( q(x) \) der Streckenlast, dem Querkraftverlauf \( Q(x) \) und dem Momentenverlauf \( M(x) \) gibt es einen festen Zusammenhang. Wenn du das Arbeitsblatt aus dem letzten Abschnitt bearbeitet hast, hast du dir das für den Zusammenhang von \( Q(x) \) und \( M(x) \) schon ein stückweit klargemacht.
Ganz allgemein gilt:

Zusammenhang der Schnittgrößen Querkraft \( Q(x) \) und Moment \( M(x) \) und der Streckenlast \( q(x) \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Zusammenhang_der_Schnittgroessen.png
Die verschiedenen Verläufe hängen also über die Ableitung zusammen. Schauen wir uns das für zwei Beispiele, die du aus dem vorangegangenen Abschnitt schon kennst, noch einmal an.
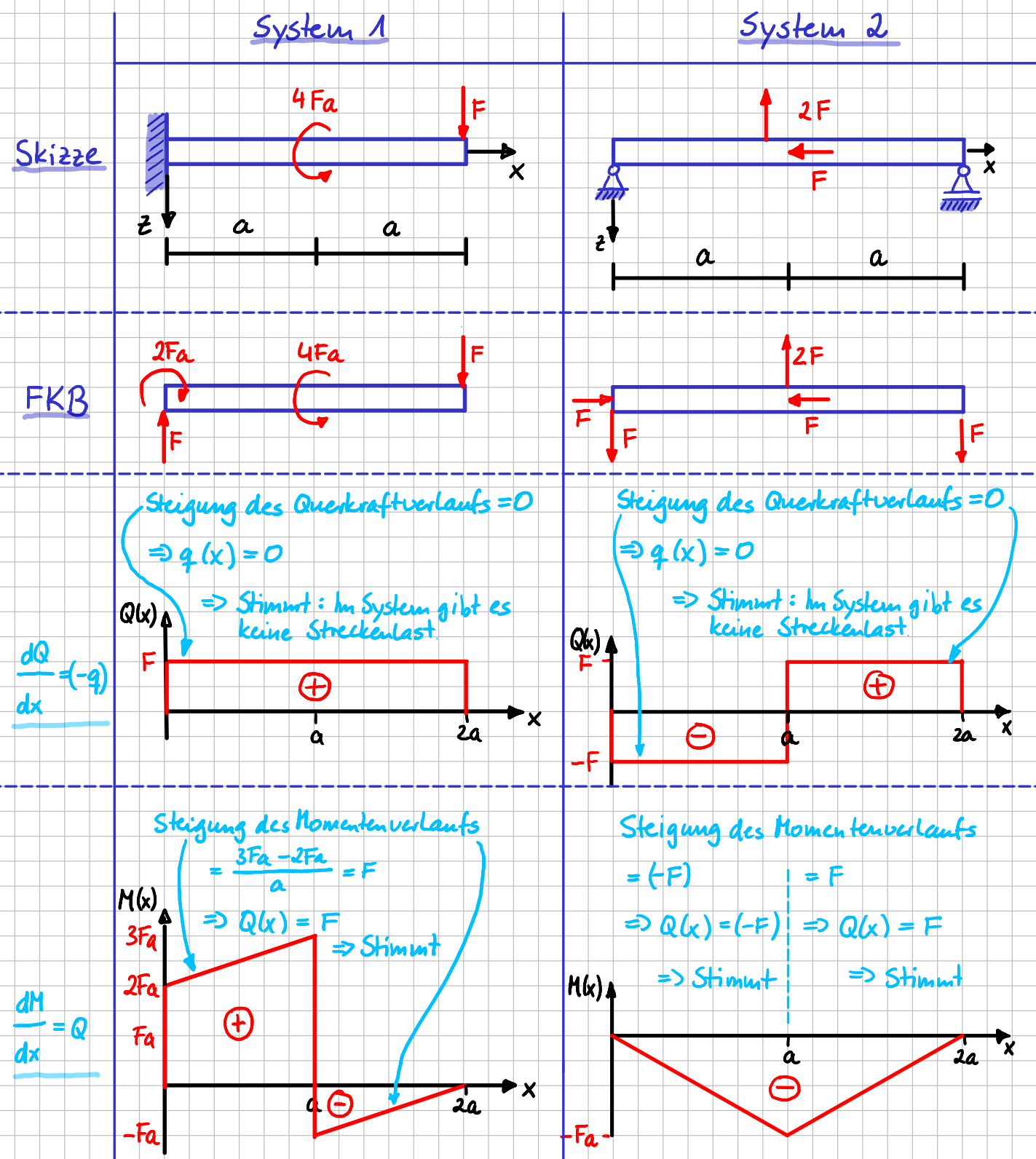
Zusammenhang der Schnittgrößen Querkraft \( Q \) und Moment \( M \) und der Streckenlast \( q \) an zwei konkreten Beispielen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Zusammenhang_der_Schnittgroessen_zwei_konkrete_Beispiele.png
In beiden Systemen ist die Steigung des Querkraftverlaufes über die gesamte Balkenlänge Null. Daran ändert der Sprung auf der Hälfte des Balkens im zweiten System auch nichts. Diese Aussage ist gleichbedeutend mit der Tatsache, dass \( q(x)=0 \) über die gesamte Balken länge gelten muss, was stimmt, da in beiden Systemen keine Streckenlast angreift.
Im ersten System ist die Steigung des Momentenverlaufs für alle \( x \)-Werte entlang des Balkens konstant und hat den Wert \( F \). Wie vorausgesagt, stimmt dieser Wert mit dem Wert der Querkraft für alle \( x \) überein. Beim zweiten System ist der Verlauf des Moments linear und zunächst negativ. Die Steigung ist \( -F \). Ab der Mitte steigt der Verlauf mit der vom Betrag her gleichen Steigung wieder an. Die Steigung ist jetzt \( +F \). Die Werte der Querkraft passen zu den Werten der Steigung im Momentenverlauf. Auch hier gilt, dass natürlich Sprünge im Querkraftverlauf auftreten können.
Die Formeln für die Schnittgrößen lassen sich natürlich auch so umstellen, dass du den Querkraft- und den Momentenverlauf aus dem Streckenlastverlauf berechnen kannst. (Für alle die, die in Mathe schon so weit sind: das geschieht durch Trennung der Variablen und anschließendem Integrieren.)

Zusammenhang der Schnittgrößen Querkraft \( Q \) und Moment \( M \) und der Streckenlast \( q \) in Integralform
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Zusammenhang_der_Schnittgroessen_in_Integralform.png
Die beiden \( C \)s sind Integrationskonstanten, die aus Randbedingungen berechnet werden müssen. Wie wir mit diesen Formeln arbeiten können, schauen wir uns etwas später auch noch für das System 1 von eben an. Für den Einstieg nehmen wir aber erstmal dieses System: Es ist ein einseitig fest eingespannter Balken mit einer konstanten Streckenlast. Das könnte z.B. ein einfaches Modell eines Flugzeugflügels sein, dessen Belastung rein durch die Auftriebskraft untersucht werden soll.
Ausgehend von der konstanten Streckenlast werden in Schritt 1 die Funktionen für die Querkraft und das Moment durch Integration bestimmt. In Schritt 2 bestimmst du dann noch die Werte der beiden Integrationskonstanten \( C_1 \) und \( C_2 \) ermitteln. Da am rechten Ende des Balkens keine Einzelkräfte oder Einzelmomente angreifen, müssen sowohl Querkraft als auch Moment hier verschwinden: \( Q(x=\ell) = 0 \) und \( M(x=\ell) =0 \). Damit hast du zwei weitere Bedingungen für die beiden unbekannten Integrationskonstanten zur Verfügung.
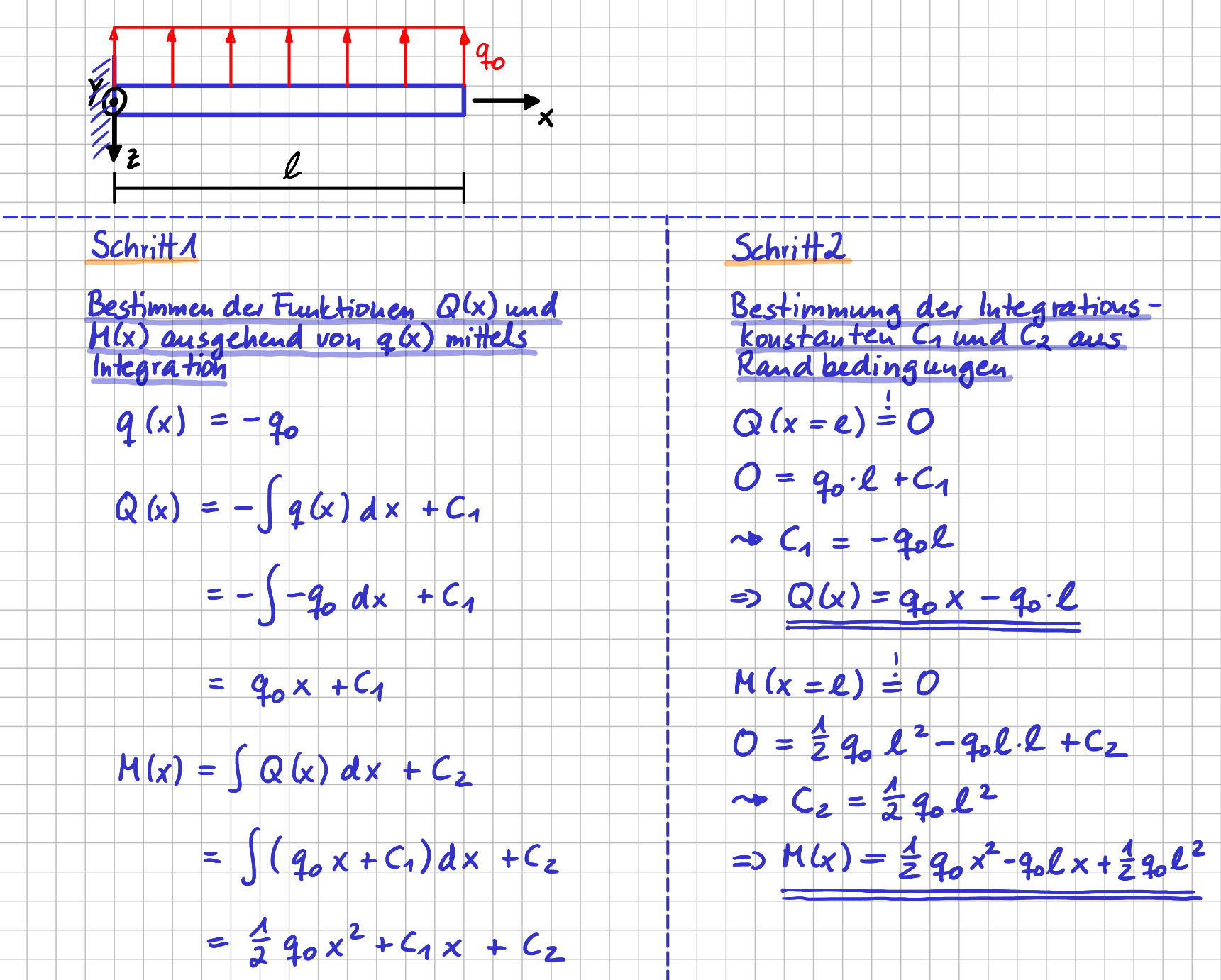
Flugzeugflügel: Bestimmung der Schnittgrößenverläufe durch Integration und Auswerten von Randbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Flugzeugfluegel.png
Dann kannst du schon die Verläufe zeichnen. Weißt du jetzt, warum du dich vermutlich mit Kurvendiskussion recht intensiv in der Schule beschäftigt hast? Hier hast du einen sehr schönen Fall, in dem du dein Wissen auffrischen und anwenden kannst.
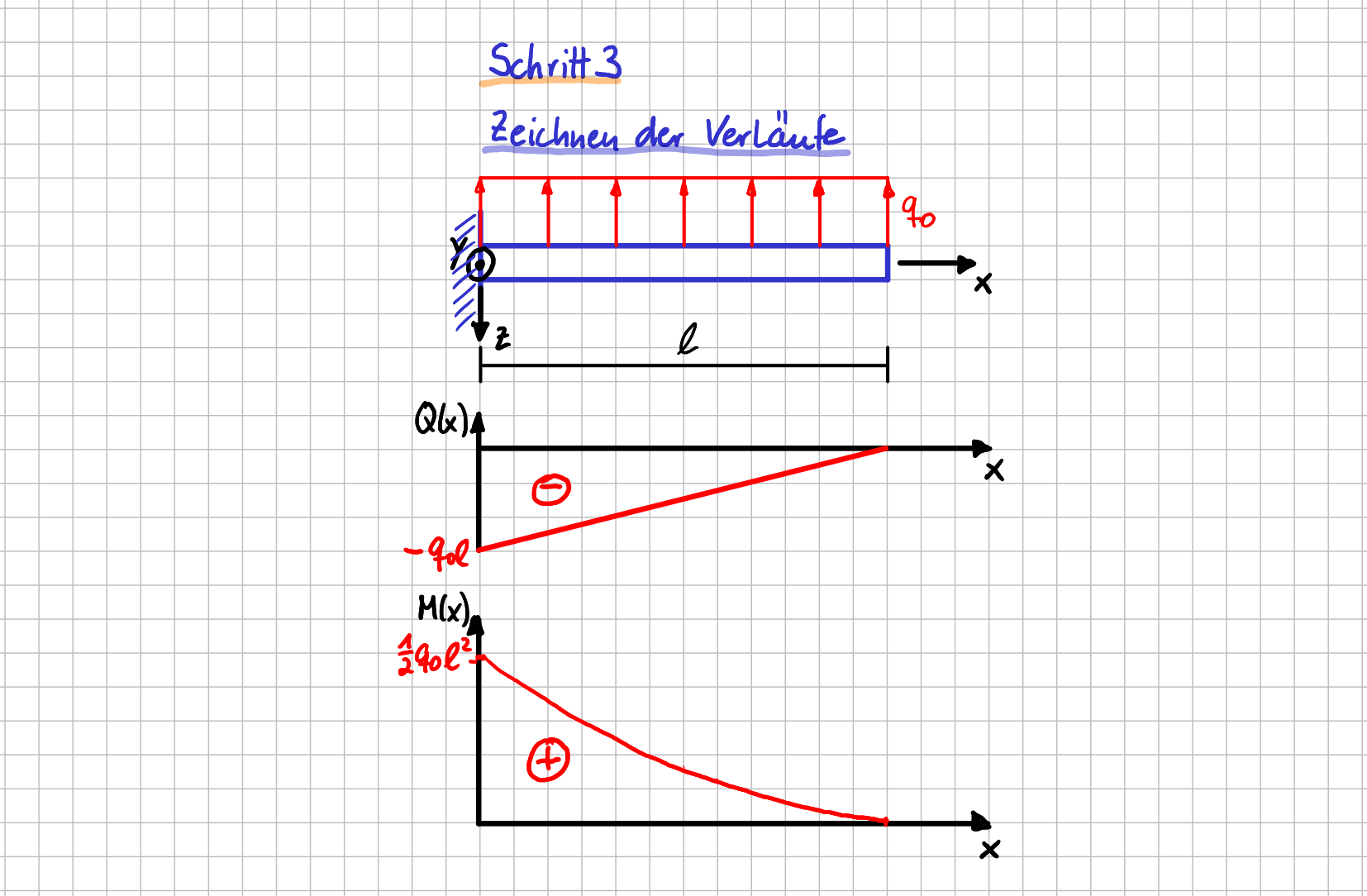
Flugzeugflügel: Zeichnen der Schnittgrößenverläufe
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Flugzeugfluegel_zeichnen_der_Schnittgroessenverlaeufe.png
Wenn du dich gewundert hast, dass wir gar nicht vorab die Lagerreaktionen bestimmt haben, dann hast du mit dieser Beobachtung total recht. Bei dem Vorgehen über das Integrieren musst du die Lagerreaktionen nämlich gar nicht vorab berechnen. Du kannst sie am Ende aus den Verläufen ablesen. (Wenn du sie schon vorab berechnet hättest, hättest du diese Informationen natürlich auch bei der Bestimmung der Integrationskonstanten verwenden können.)
Wenn du dir unsicher bist, wie das mit den Vorzeichen ist, dann mach dir doch eben in Gedanken oder real eine kurze Skizze vom Freikörperbild eines kleinen Balkenstücks, dass die freigeschnittene Lagerstelle enthält. Und dann stell die Gleichgewichtsbedingungen auf. Und dann ist das mit den Vorzeichen auf einmal ganz einfach, oder?

Flugzeugflügel: Ablesen der Lagerreaktionen aus den Schnittgrößenverläufen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Flugzeugfluegel_ablesen_der_Lagerreaktionen.png
Bleibt jetzt noch die Frage, wie das Vorgehen ist, wenn ein Balken so belastet ist, dass er für die mathematische Beschreibung in mehrere Abschnitte unterteilt werden muss. Das hast du ja im vorherigen Abschnitt prinzipiell schon geübt. Wir schauen uns nochmal das System 2 von eben an. Um es uns bei der Schreibweise möglichst einfach zu machen, definieren wir für die einzelnen Abschnitte separate \( x \)-Koordinaten \( x_I \) und \( x_{II} \).
\( x_I \) läuft von \( 0 \) bis \( a \). \( x_{II} \) läuft ebenfalls von \( 0 \) bis \( a \). So ist der Balken mit der Gesamtlänge \( 2a \) also in zwei Abschnitte aufgeteilt.
Und dann starten wir einfach wie eben auch: die Funktionen für die Streckenlasten aufstellen (Wenn keine Streckenlast vorhanden ist, ist die Funktion eben Null) und zweimal integrieren.
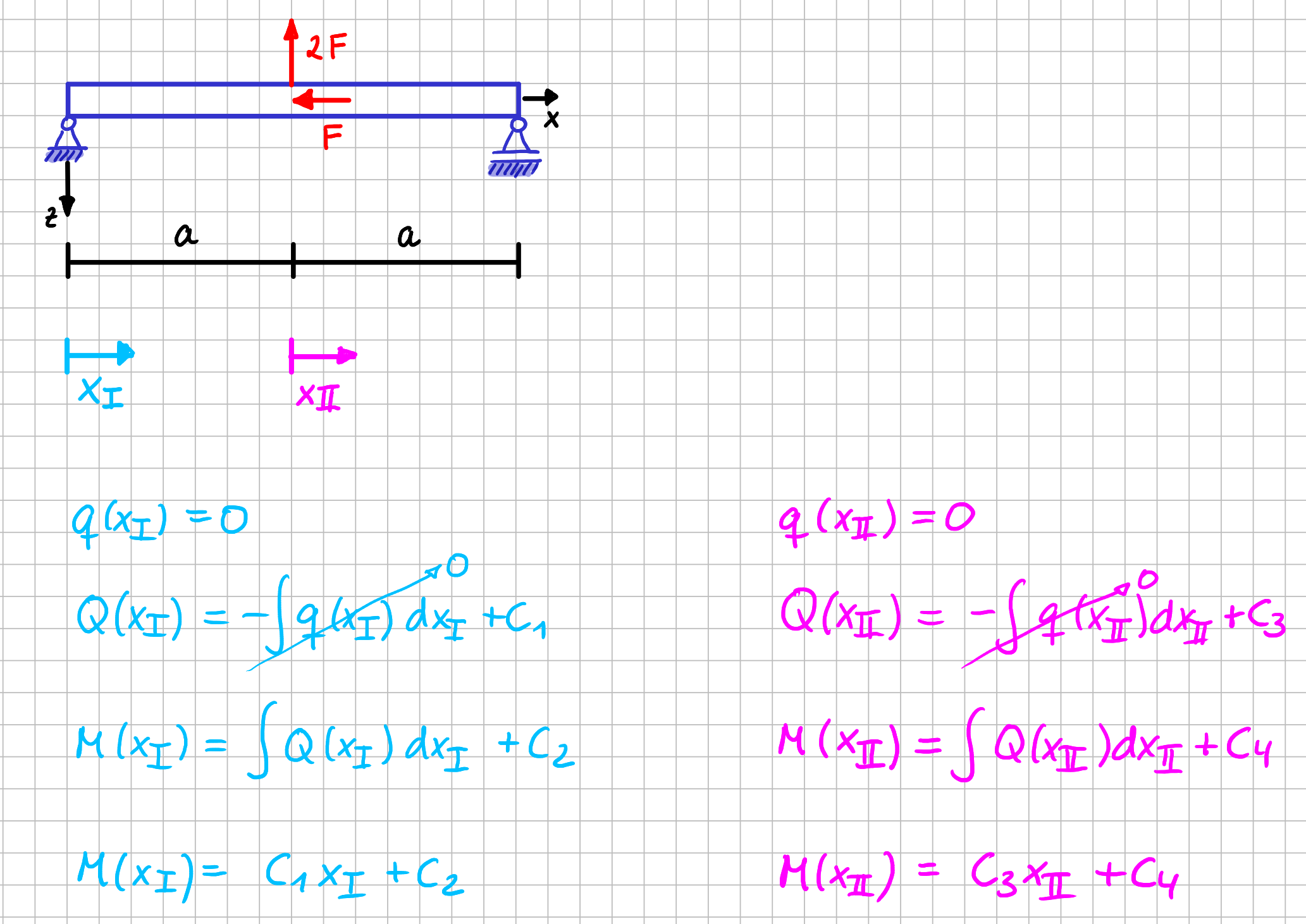
Abschnittsweise Betrachtung mit Integration am Beispiel des Systems 2
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Abschnittsweise_Betrachtung_der_Integration.png
Damit die vier Funktionen \( Q(x_I) \), \( Q(x_{II}) \), \( M(x_I) \) und \( M(x_{II}) \) vollständig bestimmt sind, musst du noch Werte für die vier Integrationsvariablen \( C_1 \), \( C_2 \), \( C_3 \) und \( C_4 \) ermitteln. Dazu benötigst du Randbedingungen und Übergangsbedingungen. Zwei Randbedingungen ergeben sich aus der Art, wie das System an den beiden Enden gelagert ist.

Randbedingungen aufgrund der Lagerung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Randbedingungen_aufgrund_der_Lagerung.png
Und dann gibt es am Übergang von \( x_I \) zu \( x_{II} \) noch zwei sogenannte Übergangsbedingungen; eine für die Querkraft und eine für das Moment. Um dir diese beiden Zusammenhänge klarzumachen, musst du wieder nur das tun, was du schon ganz oft getan hast: Freischneiden und Gleichgewichtsbedingungen aufstellen. Dieses Mal schneidest du ein ganz kleines Balken Stück im Übergangsbereich, also bei \( x=a \) heraus.

Übergangsbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Uebergangsbedingungen.png
Wie du siehst, sind die Querkraft- und Momentenwerte für \( x_I \rightarrow a \) und \( x_{II} \rightarrow 0 \) direkt gekoppelt. Mit den zwei Gleichungen aus den Randbedingungen und den zwei Gleichungen aus den Übergangsbedingungen hast du insgesamt vier Gleichungen, aus denen du die vier unbekannten Integrationskonstanten bestimmen kannst.
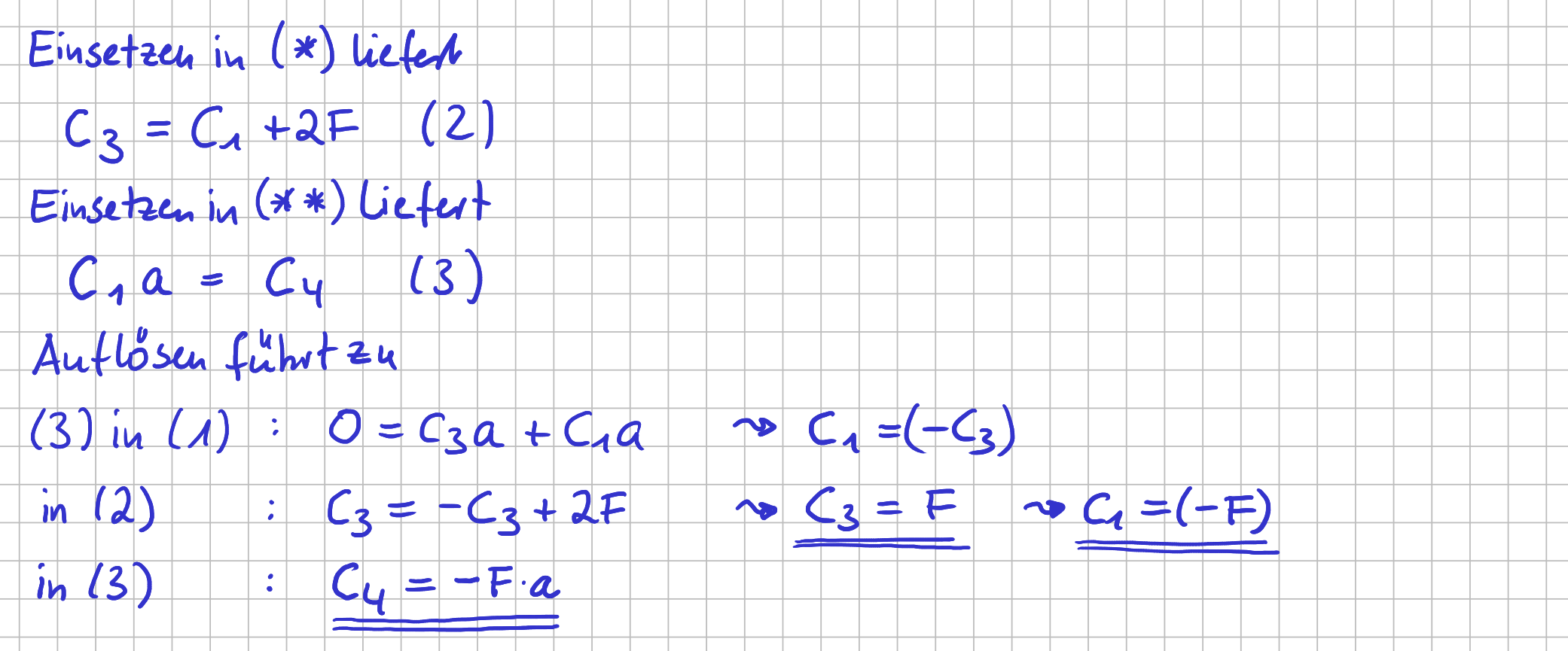
Auflösen nach den Integrationskonstanten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Aufloesen_nach_den_Integrationskonstanten.png
Damit kannst du die Gleichungen für die Schnittgrößen für die beiden Abschnitte hinschreiben und auch die Graphen zeichnen.
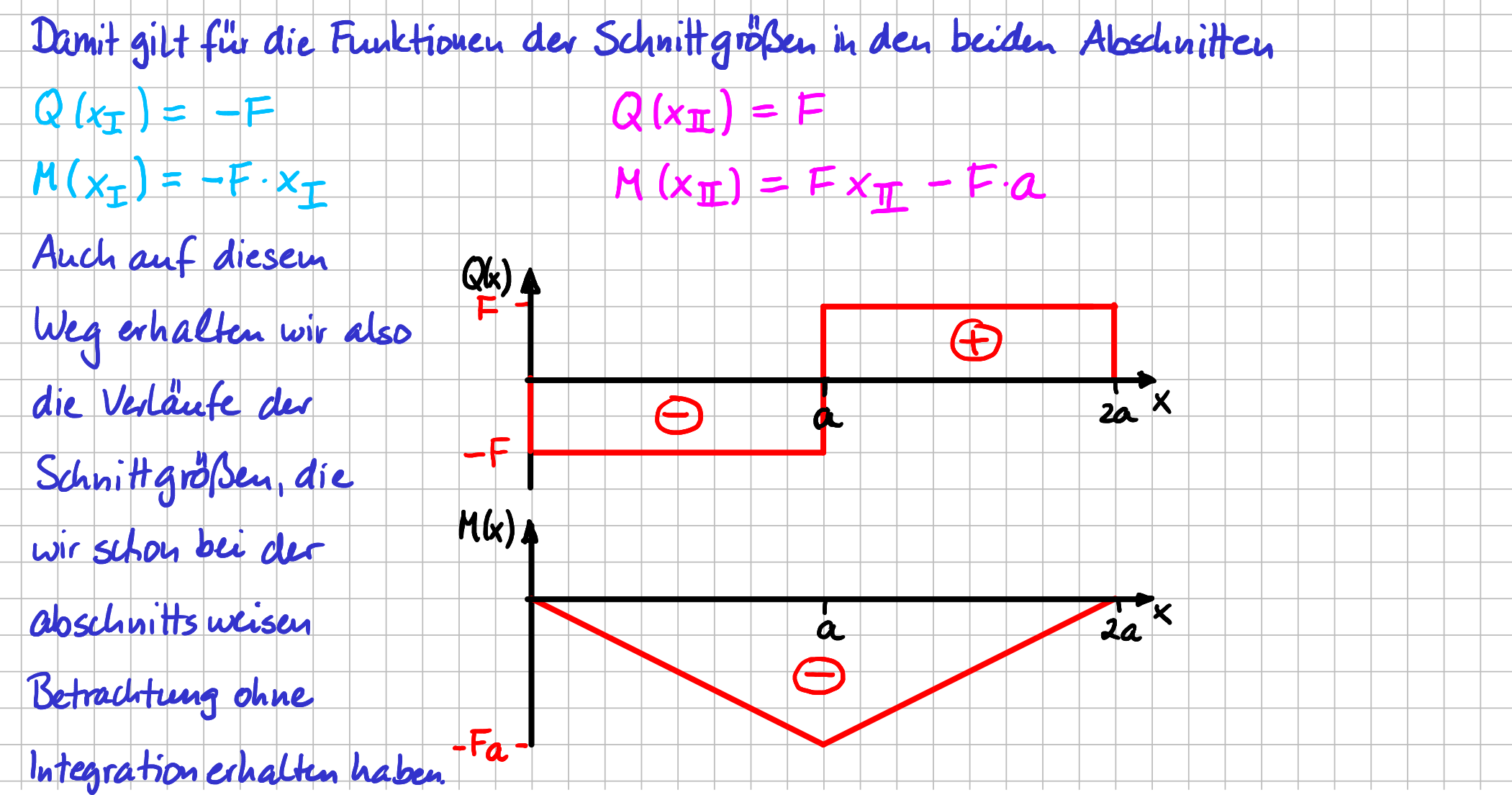
Funktionen und Graphen für die Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Funktionen_und_Graphen_fuer_die_Schnittgroessen.png
Natürlich kommt dasselbe heraus, wie bei der abschnittsweisen Betrachtung ohne Integration. Vielleicht findest du den Weg mit Integration \( - \) rein mathematisch betrachtet\( - \) schon ein wenig eleganter. Wenn dem so ist, dass wirst du die Föppl-Schreibweise, um die es im nächsten Abschnitt geht, sehr schätzen. Sie ermöglicht dir, mit Integration zu arbeiten, ohne einen Balken in Abschnitte unterteilen zu müssen. Dieses Vorgehen ist natürlich insbesondere bei Balken mit komplexen Belastungen, bei denen du mehr als zwei Abschnitte einführen müsstest, sehr elegant. Um es aber nochmal zu betonen: Alle der dann insgesamt drei betrachtete Wege führen zum selben Ergebnis. Die Physik bzw. Mechanik der System ist ja immer dieselbe. Lediglich der mathematische Zugang ist ein anderer.
Arbeitsblatt - Teste dein Wissen
 Olympisches Allerlei
Olympisches Allerlei
 Schnittgrößen meets Integration: Ein Balken, zwei verschiedene Lagerungen
Schnittgrößen meets Integration: Ein Balken, zwei verschiedene Lagerungen
 Schnittgrößen meets Integration: Zwei Systeme, unterschiedliche Belastungen
Schnittgrößen meets Integration: Zwei Systeme, unterschiedliche Belastungen
 Schnittgrößen bestimmen: durch Integration der Streckenlastfunktion
Schnittgrößen bestimmen: durch Integration der Streckenlastfunktion
 Rahmen mit Streckenlast und Einzelkraft
Rahmen mit Streckenlast und Einzelkraft
 Balken mit sinusförmiger Streckenlast
Balken mit sinusförmiger Streckenlast