Zum Hauptinhalt
Details

Schnittgrößen

Schnittgrößen

Zurück

4. Berechnung mittels Integration / Ableitung

Berechnung mittels Integration / Ableitung

Wenn du die Inhalte des vorangegangenen Abschnitts gut durchgearbeitet und verinnerlicht hast, ist es an der Zeit, einen Schritt weiterzugehen.

Zwischen dem Verlauf \( q(x) \) der Streckenlast, dem Querkraftverlauf \( Q(x) \) und dem Momentenverlauf \( M(x) \) gibt es einen festen Zusammenhang. Wenn du das Arbeitsblatt aus dem letzten Abschnitt bearbeitet hast, hast du dir das für den Zusammenhang von \( Q(x) \) und \( M(x) \) schon ein stückweit klargemacht.

Ganz allgemein gilt:


Zusammenhang der Schnittgrößen Querkraft \( Q(x) \) und Moment \( M(x) \) und der Streckenlast \( q(x) \)

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Zusammenhang_der_Schnittgroessen.png


Die verschiedenen Verläufe hängen also über die Ableitung zusammen. Schauen wir uns das für zwei Beispiele, die du aus dem vorangegangenen Abschnitt schon kennst, noch einmal an.


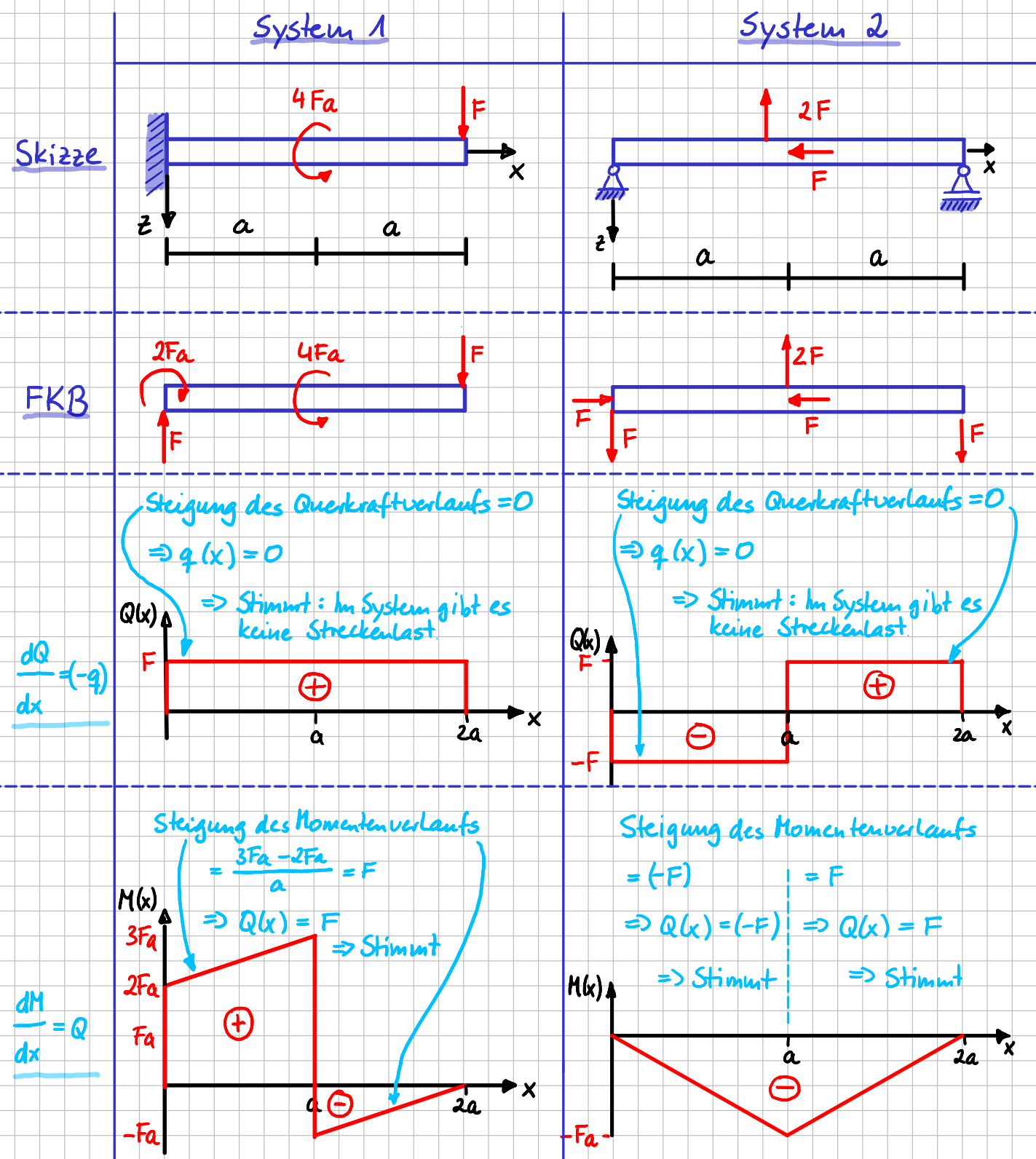
Zusammenhang der Schnittgrößen Querkraft \( Q \) und Moment \( M \) und der Streckenlast \( q \) an zwei konkreten Beispielen

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Zusammenhang_der_Schnittgroessen_zwei_konkrete_Beispiele.png


In beiden Systemen ist die Steigung des Querkraftverlaufes über die gesamte Balkenlänge Null. Daran ändert der Sprung auf der Hälfte des Balkens im zweiten System auch nichts. Diese Aussage ist gleichbedeutend mit der Tatsache, dass \( q(x)=0 \) über die gesamte Balken länge gelten muss, was stimmt, da in beiden Systemen keine Streckenlast angreift.

Im ersten System ist die Steigung des Momentenverlaufs für alle \( x \)-Werte entlang des Balkens konstant und hat den Wert \( F \). Wie vorausgesagt, stimmt dieser Wert mit dem Wert der Querkraft für alle \( x \) überein. Beim zweiten System ist der Verlauf des Moments linear und zunächst negativ. Die Steigung ist \( -F \). Ab der Mitte steigt der Verlauf mit der vom Betrag her gleichen Steigung wieder an. Die Steigung ist jetzt \( +F \). Die Werte der Querkraft passen zu den Werten der Steigung im Momentenverlauf. Auch hier gilt, dass natürlich Sprünge im Querkraftverlauf auftreten können.

Die Formeln für die Schnittgrößen lassen sich natürlich auch so umstellen, dass du den Querkraft- und den Momentenverlauf aus dem Streckenlastverlauf berechnen kannst. (Für alle die, die in Mathe schon so weit sind: das geschieht durch Trennung der Variablen und anschließendem Integrieren.)


Zusammenhang der Schnittgrößen Querkraft \( Q \) und Moment \( M \) und der Streckenlast \( q \) in Integralform

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Zusammenhang_der_Schnittgroessen_in_Integralform.png


Die beiden \( C \)s sind Integrationskonstanten, die aus Randbedingungen berechnet werden müssen. Wie wir mit diesen Formeln arbeiten können, schauen wir uns etwas später auch noch für das System 1 von eben an. Für den Einstieg nehmen wir aber erstmal dieses System: Es ist ein einseitig fest eingespannter Balken mit einer konstanten Streckenlast. Das könnte z.B. ein einfaches Modell eines Flugzeugflügels sein, dessen Belastung rein durch die Auftriebskraft untersucht werden soll.

Ausgehend von der konstanten Streckenlast werden in Schritt 1 die Funktionen für die Querkraft und das Moment durch Integration bestimmt. In Schritt 2 bestimmst du dann noch die Werte der beiden Integrationskonstanten \( C_1 \) und \( C_2 \) ermitteln. Da am rechten Ende des Balkens keine Einzelkräfte oder Einzelmomente angreifen, müssen sowohl Querkraft als auch Moment hier verschwinden: \( Q(x=\ell) = 0 \) und \( M(x=\ell) =0 \). Damit hast du zwei weitere Bedingungen für die beiden unbekannten Integrationskonstanten zur Verfügung.


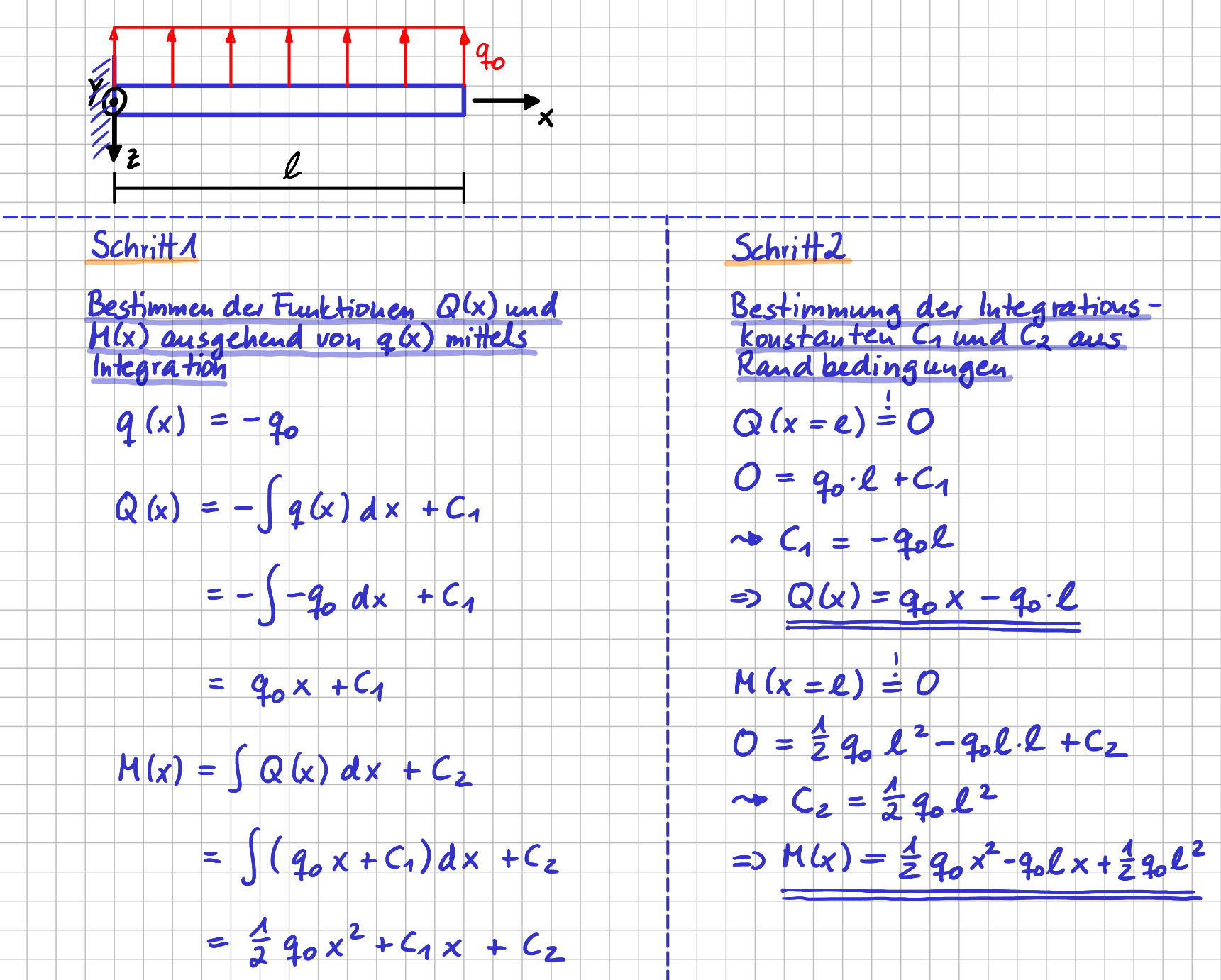
Flugzeugflügel: Bestimmung der Schnittgrößenverläufe durch Integration und Auswerten von Randbedingungen

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Flugzeugfluegel.png


Dann kannst du schon die Verläufe zeichnen. Weißt du jetzt, warum du dich vermutlich mit Kurvendiskussion recht intensiv in der Schule beschäftigt hast? Hier hast du einen sehr schönen Fall, in dem du dein Wissen auffrischen und anwenden kannst.


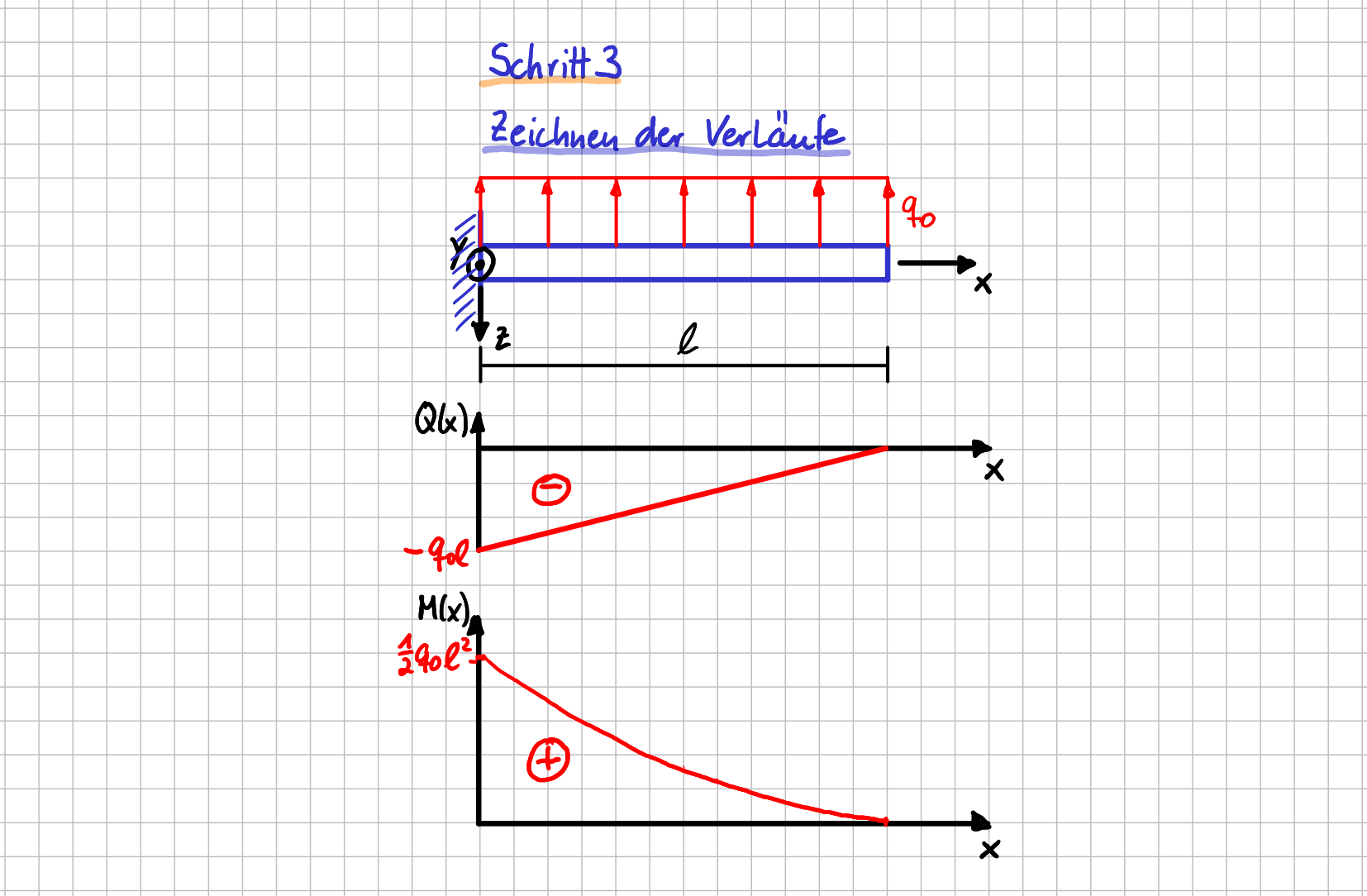
Flugzeugflügel: Zeichnen der Schnittgrößenverläufe

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Flugzeugfluegel_zeichnen_der_Schnittgroessenverlaeufe.png


Wenn du dich gewundert hast, dass wir gar nicht vorab die Lagerreaktionen bestimmt haben, dann hast du mit dieser Beobachtung total recht. Bei dem Vorgehen über das Integrieren musst du die Lagerreaktionen nämlich gar nicht vorab berechnen. Du kannst sie am Ende aus den Verläufen ablesen. (Wenn du sie schon vorab berechnet hättest, hättest du diese Informationen natürlich auch bei der Bestimmung der Integrationskonstanten verwenden können.)
Wenn du dir unsicher bist, wie das mit den Vorzeichen ist, dann mach dir doch eben in Gedanken oder real eine kurze Skizze vom Freikörperbild eines kleinen Balkenstücks, dass die freigeschnittene Lagerstelle enthält. Und dann stell die Gleichgewichtsbedingungen auf. Und dann ist das mit den Vorzeichen auf einmal ganz einfach, oder?


Flugzeugflügel: Ablesen der Lagerreaktionen aus den Schnittgrößenverläufen

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Flugzeugfluegel_ablesen_der_Lagerreaktionen.png


Bleibt jetzt noch die Frage, wie das Vorgehen ist, wenn ein Balken so belastet ist, dass er für die mathematische Beschreibung in mehrere Abschnitte unterteilt werden muss. Das hast du ja im vorherigen Abschnitt prinzipiell schon geübt. Wir schauen uns nochmal das System 2 von eben an. Um es uns bei der Schreibweise möglichst einfach zu machen, definieren wir für die einzelnen Abschnitte separate \( x \)-Koordinaten \( x_I \) und \( x_{II} \). 
\( x_I \) läuft von \( 0 \) bis \( a \). \( x_{II} \) läuft ebenfalls von \( 0 \) bis \( a \). So ist der Balken mit der Gesamtlänge \( 2a \) also in zwei Abschnitte aufgeteilt.
Und dann starten wir einfach wie eben auch: die Funktionen für die Streckenlasten aufstellen (Wenn keine Streckenlast vorhanden ist, ist die Funktion eben Null) und zweimal integrieren.


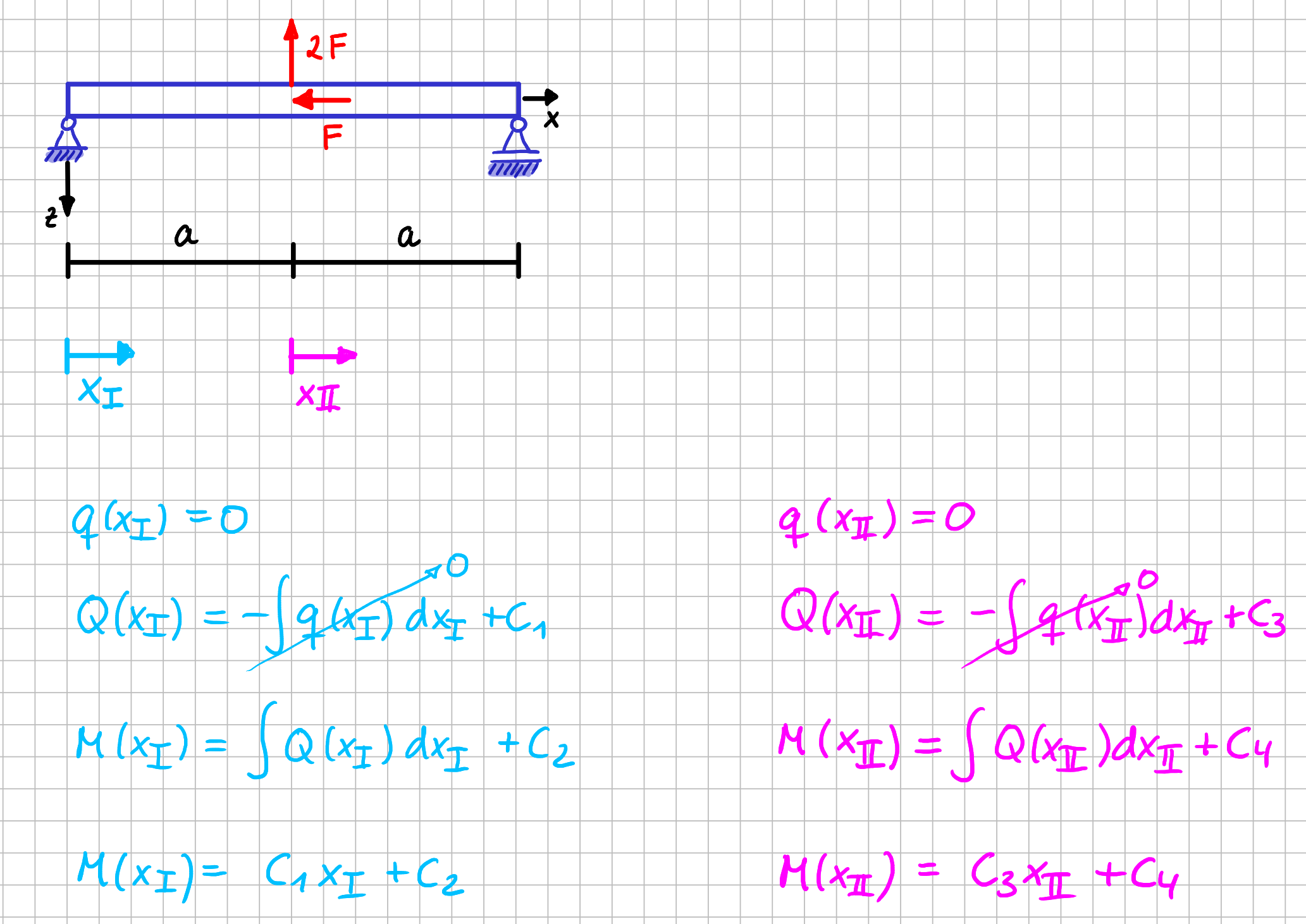
Abschnittsweise Betrachtung mit Integration am Beispiel des Systems 2

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Abschnittsweise_Betrachtung_der_Integration.png


Damit die vier Funktionen \( Q(x_I) \), \( Q(x_{II}) \), \( M(x_I) \) und \( M(x_{II}) \) vollständig bestimmt sind, musst du noch Werte für die vier Integrationsvariablen \( C_1 \), \( C_2 \), \( C_3 \) und \( C_4 \) ermitteln. Dazu benötigst du Randbedingungen und Übergangsbedingungen. Zwei Randbedingungen ergeben sich aus der Art, wie das System an den beiden Enden gelagert ist.


Randbedingungen aufgrund der Lagerung

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Randbedingungen_aufgrund_der_Lagerung.png


Und dann gibt es am Übergang von \( x_I \) zu \( x_{II} \) noch zwei sogenannte Übergangsbedingungen; eine für die Querkraft und eine für das Moment. Um dir diese beiden Zusammenhänge klarzumachen, musst du wieder nur das tun, was du schon ganz oft getan hast: Freischneiden und Gleichgewichtsbedingungen aufstellen. Dieses Mal schneidest du ein ganz kleines Balken Stück im Übergangsbereich, also bei \( x=a \) heraus.


Übergangsbedingungen

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Uebergangsbedingungen.png


Wie du siehst, sind die Querkraft- und Momentenwerte für \( x_I \rightarrow a \) und \( x_{II} \rightarrow 0 \) direkt gekoppelt. Mit den zwei Gleichungen aus den Randbedingungen und den zwei Gleichungen aus den Übergangsbedingungen hast du insgesamt vier Gleichungen, aus denen du die vier unbekannten Integrationskonstanten bestimmen kannst.


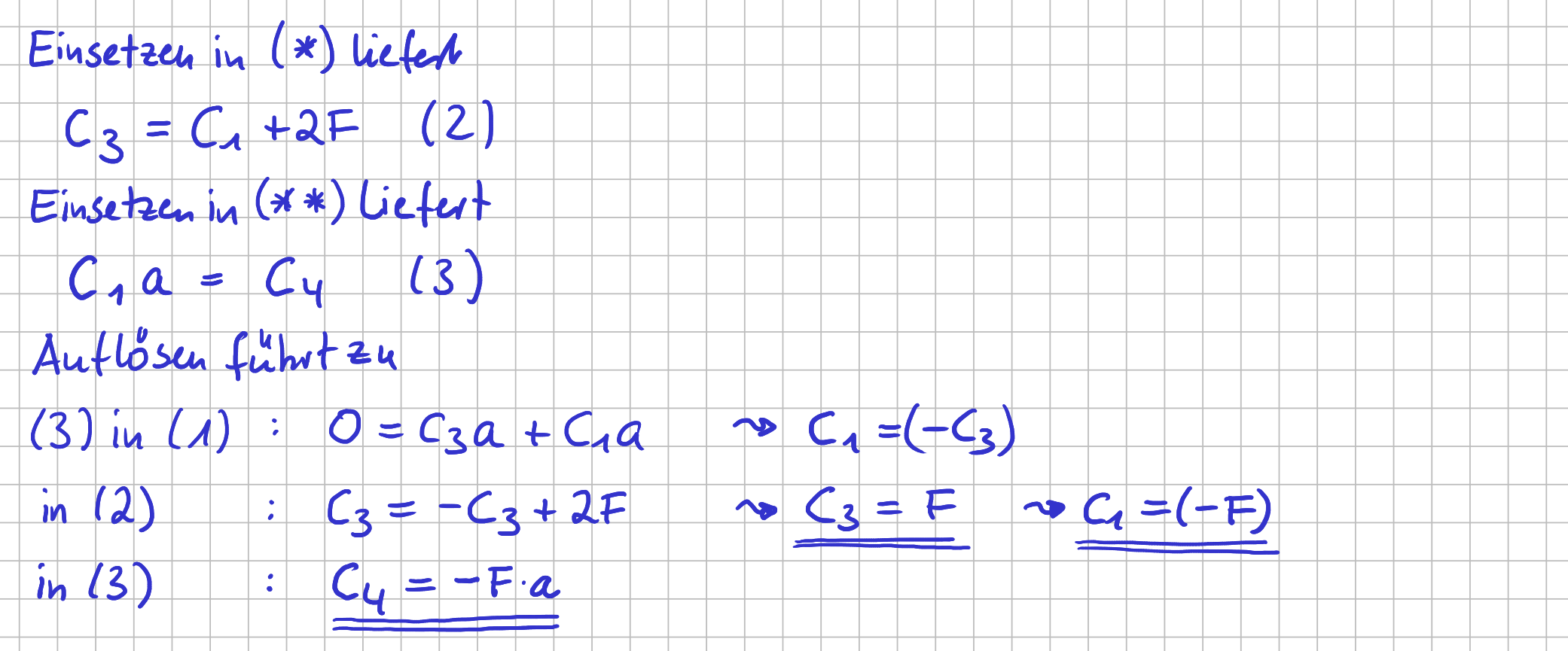
Auflösen nach den Integrationskonstanten

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Aufloesen_nach_den_Integrationskonstanten.png


Damit kannst du die Gleichungen für die Schnittgrößen für die beiden Abschnitte hinschreiben und auch die Graphen zeichnen.


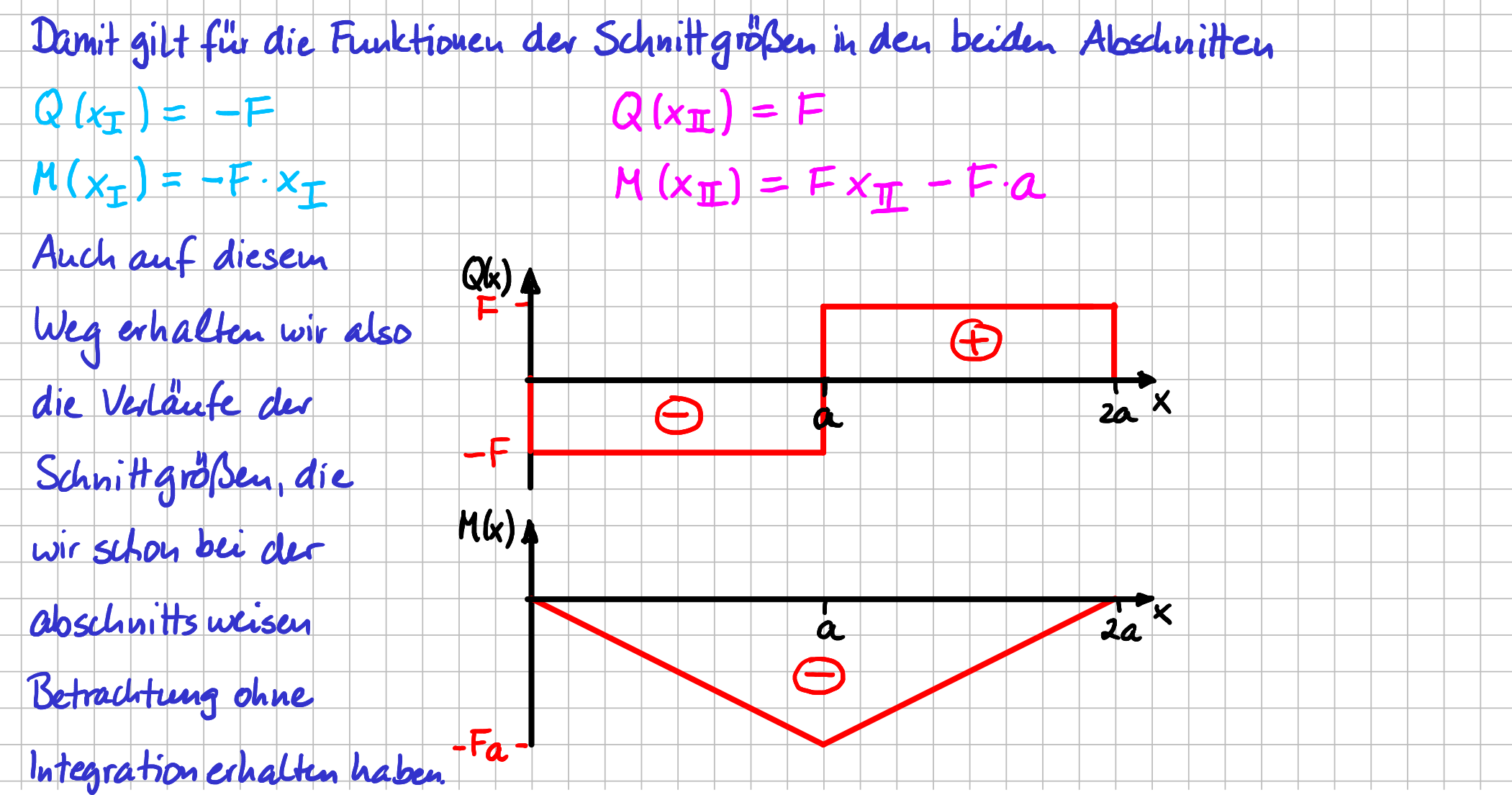
Funktionen und Graphen für die Schnittgrößen

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2218/Funktionen_und_Graphen_fuer_die_Schnittgroessen.png


Natürlich kommt dasselbe heraus, wie bei der abschnittsweisen Betrachtung ohne Integration. Vielleicht findest du den Weg mit Integration \( - \) rein mathematisch betrachtet\( - \) schon ein wenig eleganter. Wenn dem so ist, dass wirst du die Föppl-Schreibweise, um die es im nächsten Abschnitt geht, sehr schätzen. Sie ermöglicht dir, mit Integration zu arbeiten, ohne einen Balken in Abschnitte unterteilen zu müssen. Dieses Vorgehen ist natürlich insbesondere bei Balken mit komplexen Belastungen, bei denen du mehr als zwei Abschnitte einführen müsstest, sehr elegant. Um es aber nochmal zu betonen: Alle der dann insgesamt drei betrachtete Wege führen zum selben Ergebnis. Die Physik bzw. Mechanik der System ist ja immer dieselbe. Lediglich der mathematische Zugang ist ein anderer.


Zurück