Schnittgrößen
Schnittgrößen
3. Berechnung mittels Aufstellen von Gleichgewichtsbedigungen
Berechnung mittels Aufstellen von Gleichgewichtsbedigungen
Wie lassen sich Schnittgrößen denn nun berechnen?
Naja, wie du gesehen hast, war ja beim Einführen schon viel Bekanntes dabei. Dann besteht doch die Hoffnung, dass das bei der Berechnung der Schnittgrößen auch so ist, oder? Und genauso ist es.
Wir wollen uns das generelle Vorgehen an einem ganz einfachen System anschauen: Einem Balken der Länge \( 2 a \) mit Fest-Los-Lagerung und einer Einzelkraft senkrecht zur Balkenachse in der Mitte und einer Einzelkraft in Balkenrichtung am rechten Ende.
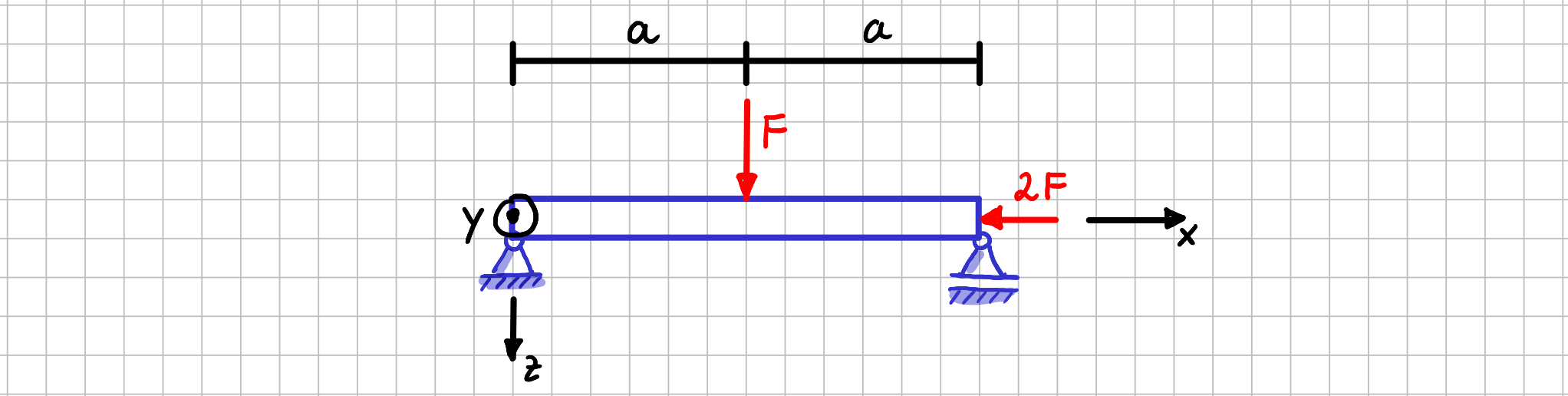
Einfaches System für den Einstieg in die Berechnung von Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Einfaches_System_Berechnung_Schnittgroessen.png
Wenn du im ersten Schritt die Lager freischneidest, ein Freikörperbild aufzeichnest und die Lagerreaktionen bestimmst, bekommst du das folgende Ergebnis.
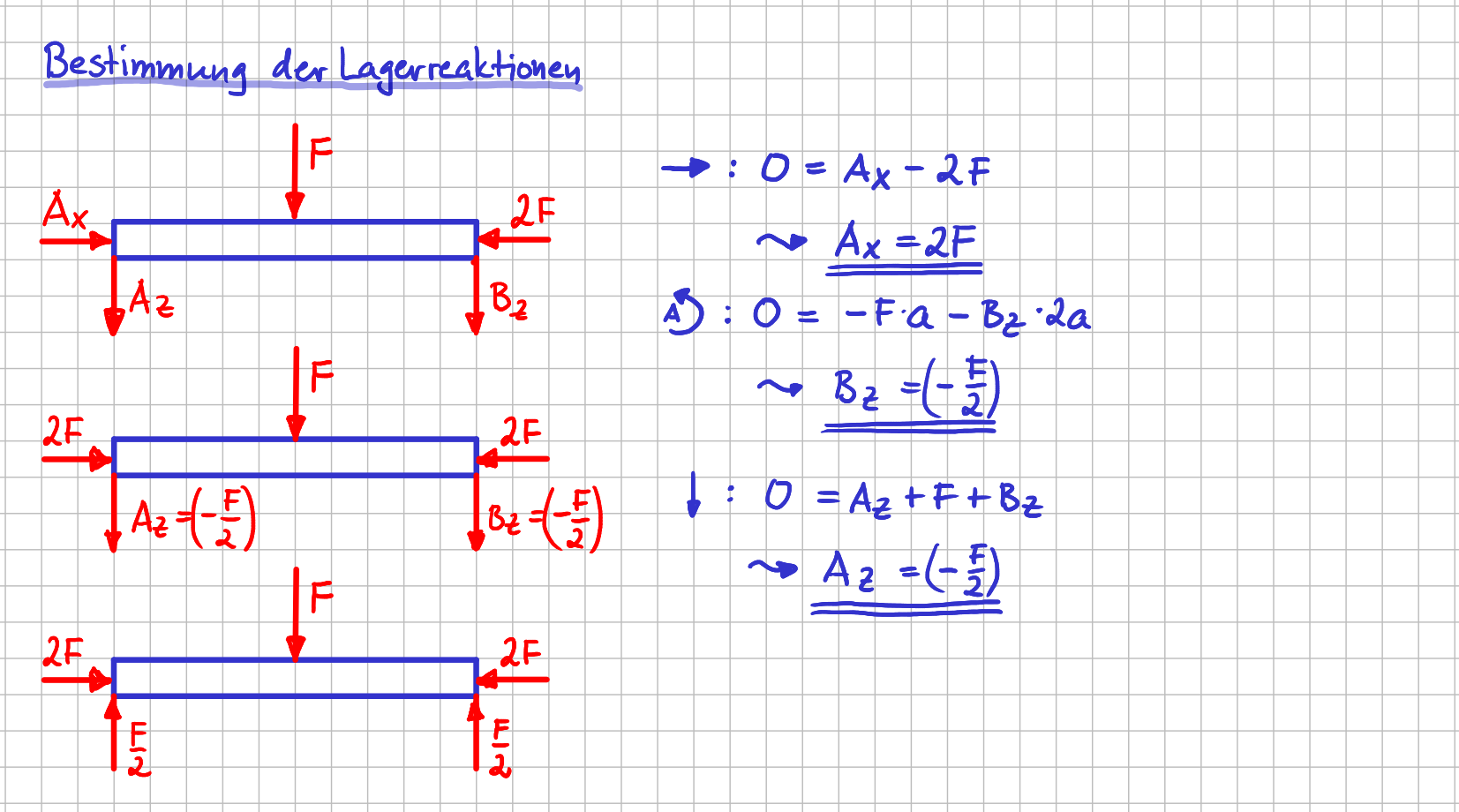
Bestimmung der Lagerreaktionen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Bestimmung_der_Lagerreaktionen.png
Vielleicht musst du für dieses einfache System inzwischen auch schon gar nicht mehr rechnen, sondern 'siehst' das Ergebnis sofort.
So, jetzt aber: Nun wollen wir ins Innere des Balkens hineinschauen und die Funktionen für die Schnittgrößen bestimmen und ihre Verläufe zeichnen.
Wenn wir den Balken irgendwo im Bereich \( 0 < x < a \) durchschneiden, sehen die Freikörperbilder der beiden Teilsysteme so aus:
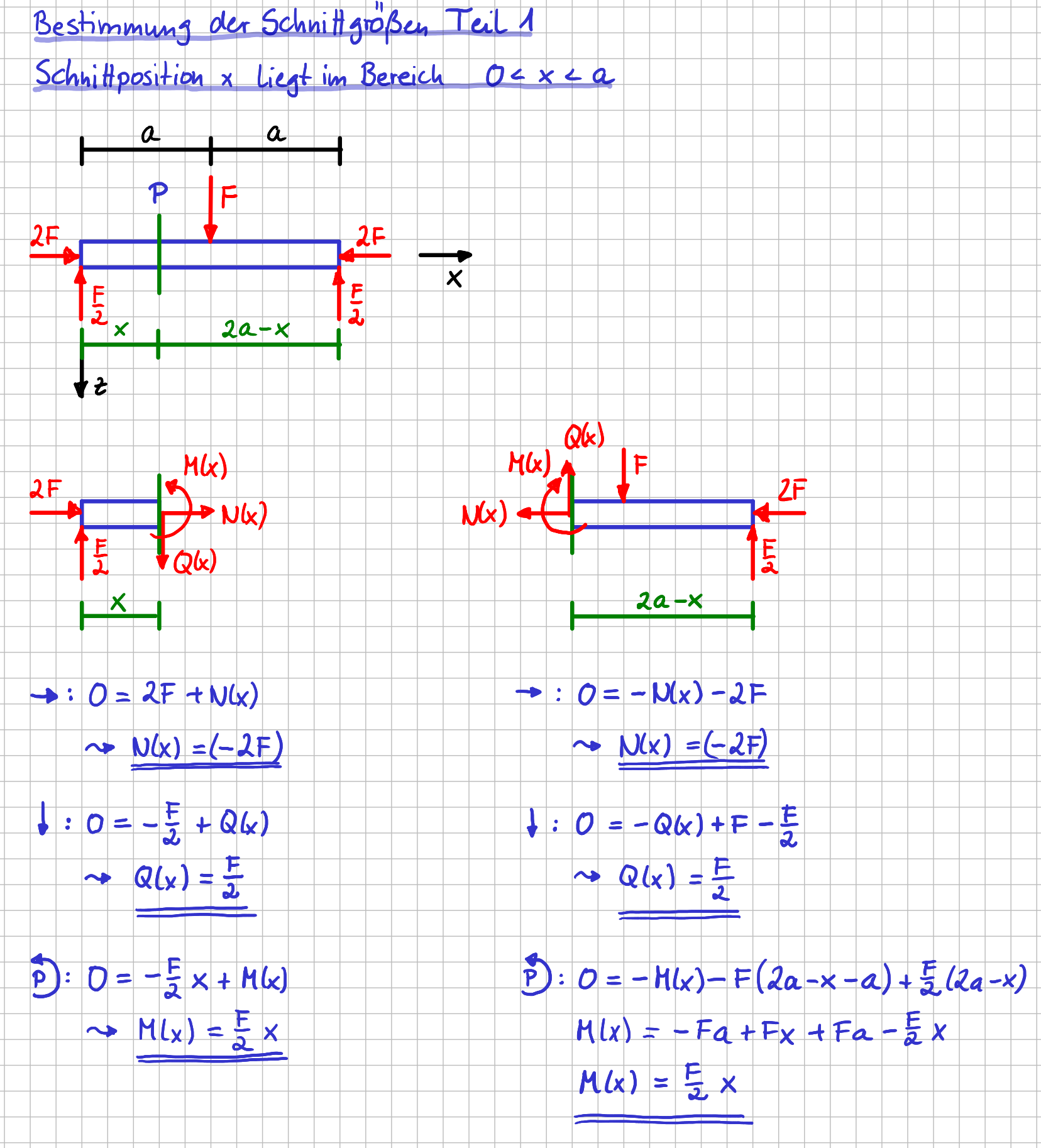
Schnitt mit Schnittposition \( x \) im Bereich \( 0 < x < a \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Schnitt_mit_Schnittposition_1.png
Wenn du die Gleichgewichtsbedingungen aufstellst siehst du, dass du in diesem Beispiel jeweils eine Gleichung direkt nach einer der gesuchten Schnittgrößen \( N \) , \( Q \) und \( M \) auflösen kannst. Dabei ist es egal, ob du die Gleichungen für das linke oder das rechte Teilsystem aufstellst. Das wiederum ist ja völlig logisch, da in der Statik auch jedes herausgeschnittene Teilsystem wieder im Gleichgewicht ist, wenn an der Schnittstelle geeignete Reaktionsgrößen berücksichtigt werden und genau das haben wir ja getan.
An der Stelle \( x=a \) passiert etwas im System: dort greift die Kraft \( F \) an. Das bedeutet, dass sich die Qualität des Freikörperbilds ändert. Daher musst du in einem zweiten Schritt betrachten, was passiert, wenn der Schnitt im Bereich \( a < x < 2a \) liegt.
Achtung: Dieser Bereich gibt nur die Lage der Schnittposition an. Die beiden sich ergebenden Teilsysteme des Balkens haben natürlich trotzdem ihre volle Länge.
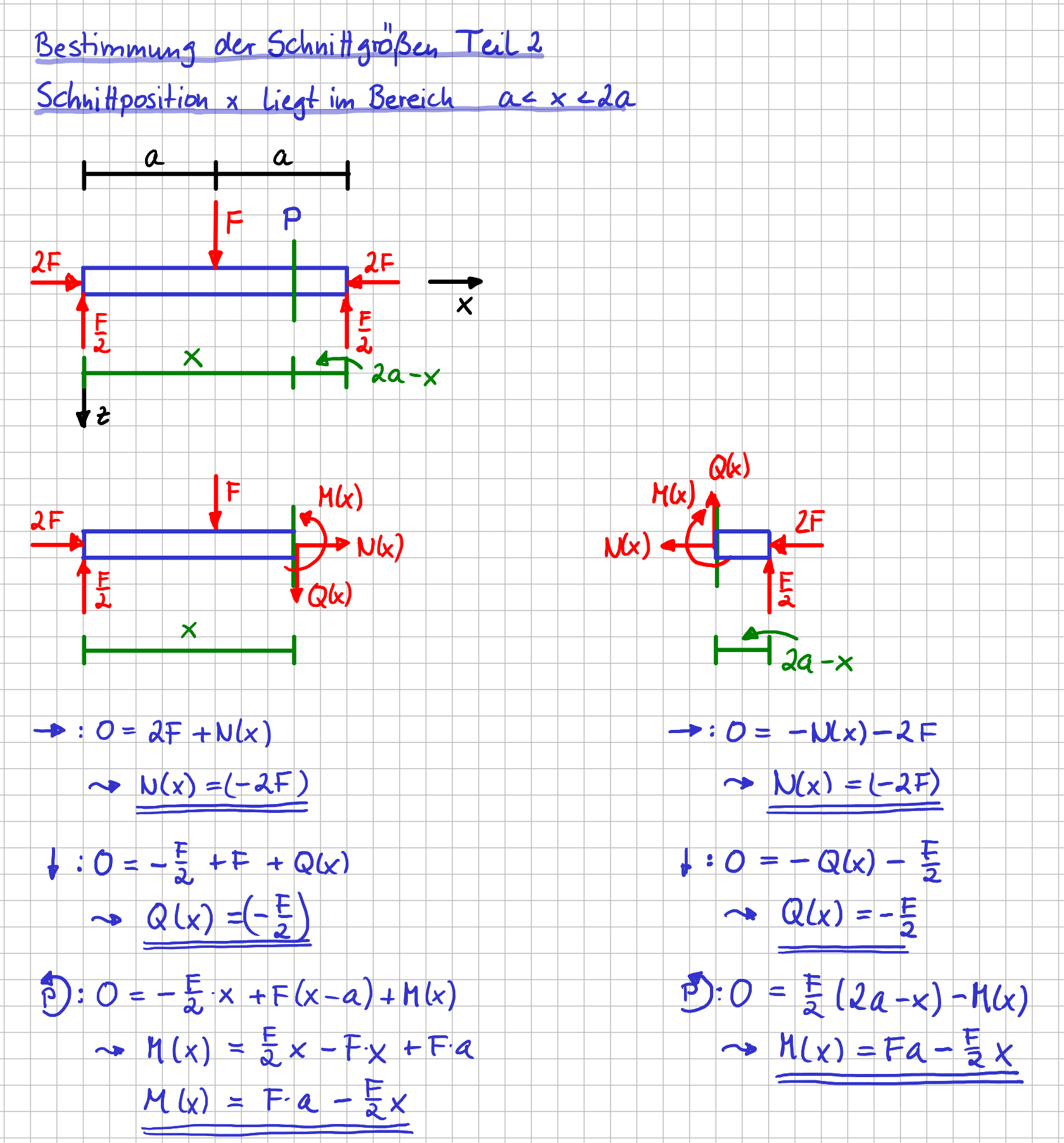
Schnitt mit Schnittposition \( x \) im Bereich \( a < x < 2a \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Schnitt_mit_Schnittposition_2.png
Wenn du wieder die Gleichgewichtsbedingungen aufstellst und auswertest, kannst du wieder direkt nach den gesuchten Schnittgrößen auflösen.
Du hast also für die beiden unterschiedlichen Bereiche, in denen sich die Schnittposition \( x \) bewegen kann, ohne dass sich die Qualität der Freikörperbilder der Teilsysteme ändert, Funktionen für die drei Schnittgrößen Normalkraft \( N(x) \), Querkraft \( Q(x) \) und Biegemoment \( M(x) \) bekommen.
Diese Verläufe kannst du in Diagramme zeichnen. Das sieht dann so aus.
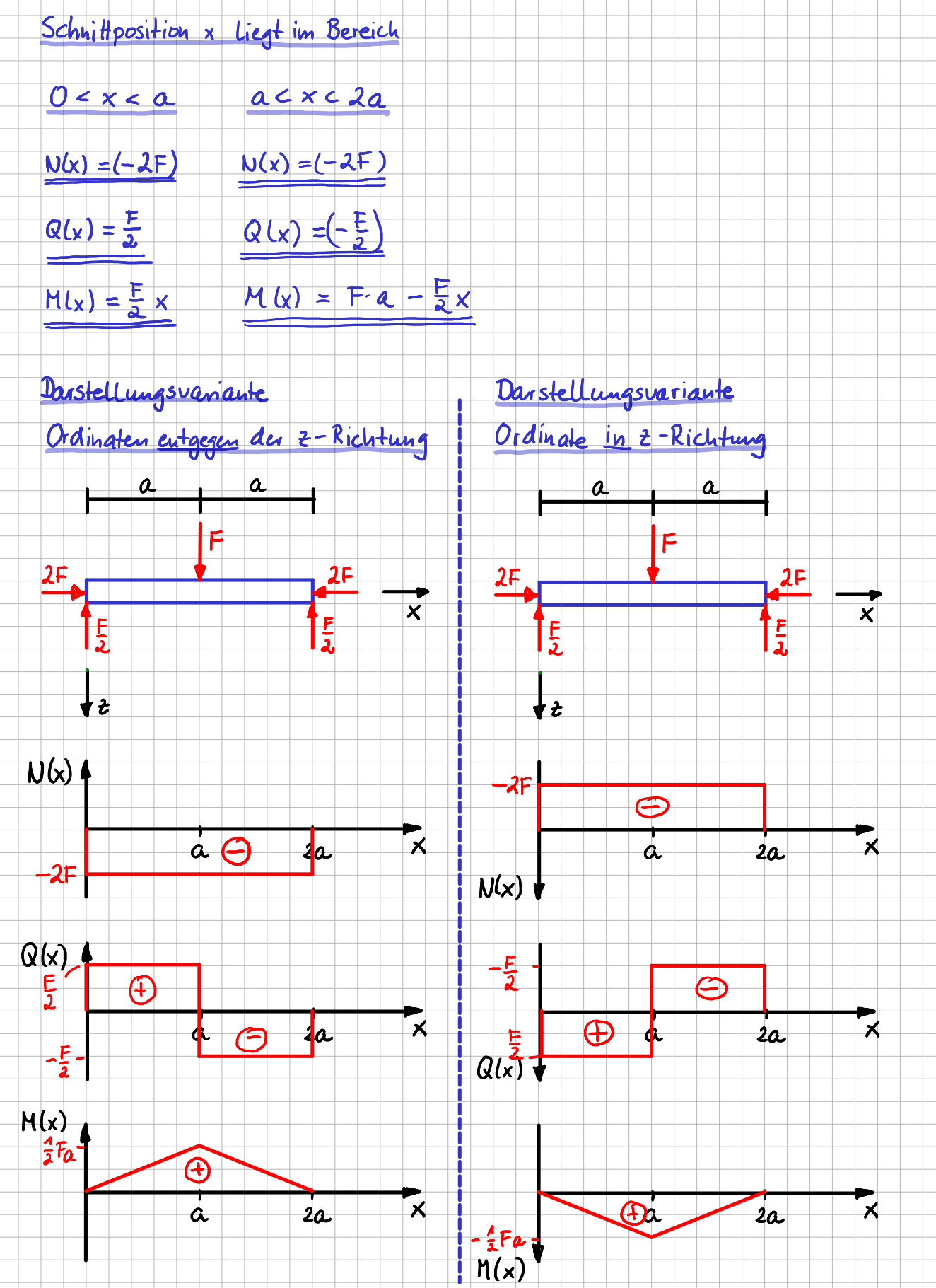
Darstellung der Verläufe der Schnittgrößen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Darstellung_der_Verlaeufe.png
Es gibt verschiedene Arten, wie du die Verläufe darstellen kannst. Einige Berufszweige und damit auch Lehrbücher befürworten es, die Ordinate der Diagramme 'nach oben' also entgegen der positiven \( z \)-Richtung einzuzeichnen. Andere zeichnen die Achsen 'nach unten' also in positive \( z \)- Richtung ein. Auch eine Mischform kommt vor.
Deswegen habe ich dir in der vorherigen Abbildung zwei verschiedene Varianten aufgezeichnet.
Was auch ohne Zeichnen der Verläufe schon klar war: die Werte der Normalkraft sind vollständig entkoppelt von dem, was in \( z \)-Richtung los ist, also vom Querkraft- und Momentenverlauf. Beim Querkraft- und Momentenverlauf hingegen kannst du vielleicht schon einen Zusammenhang erkennen, oder? Wenn du dir den Momentenverlauf anschaust und mal die Steigung der gezeigten Kurve betrachtest: Was fällt dir auf?
Genau, die Steigung des Momentenverlaufs entspricht gerade dem Wert der Querkraft an der entsprechenden Stelle. Genau auf diese Art der Zusammenhänge und die sich daraus ergebenden Konsequenzen für die Berechnung von Schnittgrößen gehen wir im nächsten Abschnitt weiter ein.
Bleibt noch die Frage: Und wie ist das Vorgehen bei der abschnittsweisen Betrachtung, wenn eine Streckenlast vorhanden ist? Eigentlich gehst du nicht wirklich anders mit einer Streckenlast um, als du es tust, wenn du die Lagerreaktionen für das Gesamtsystem bestimmst. Dort fasst du die Streckenlast ja zu einer resultierenden Einzelkraft zusammen.
Ich habe hier nochmal ein Beispiel mit einer dreiecksförmigen Streckenlast für dich. Wenn du nochmal Schritt für Schritt sehen möchtest, wie du die resultierende Einzelkraft bestimmst, schau gerne in der Lektion Grundgrößen \( \rightarrow \) Kraft \( \rightarrow \) Verschiedene Kräfte ganz nah \( \rightarrow \) Streckenlast nach.
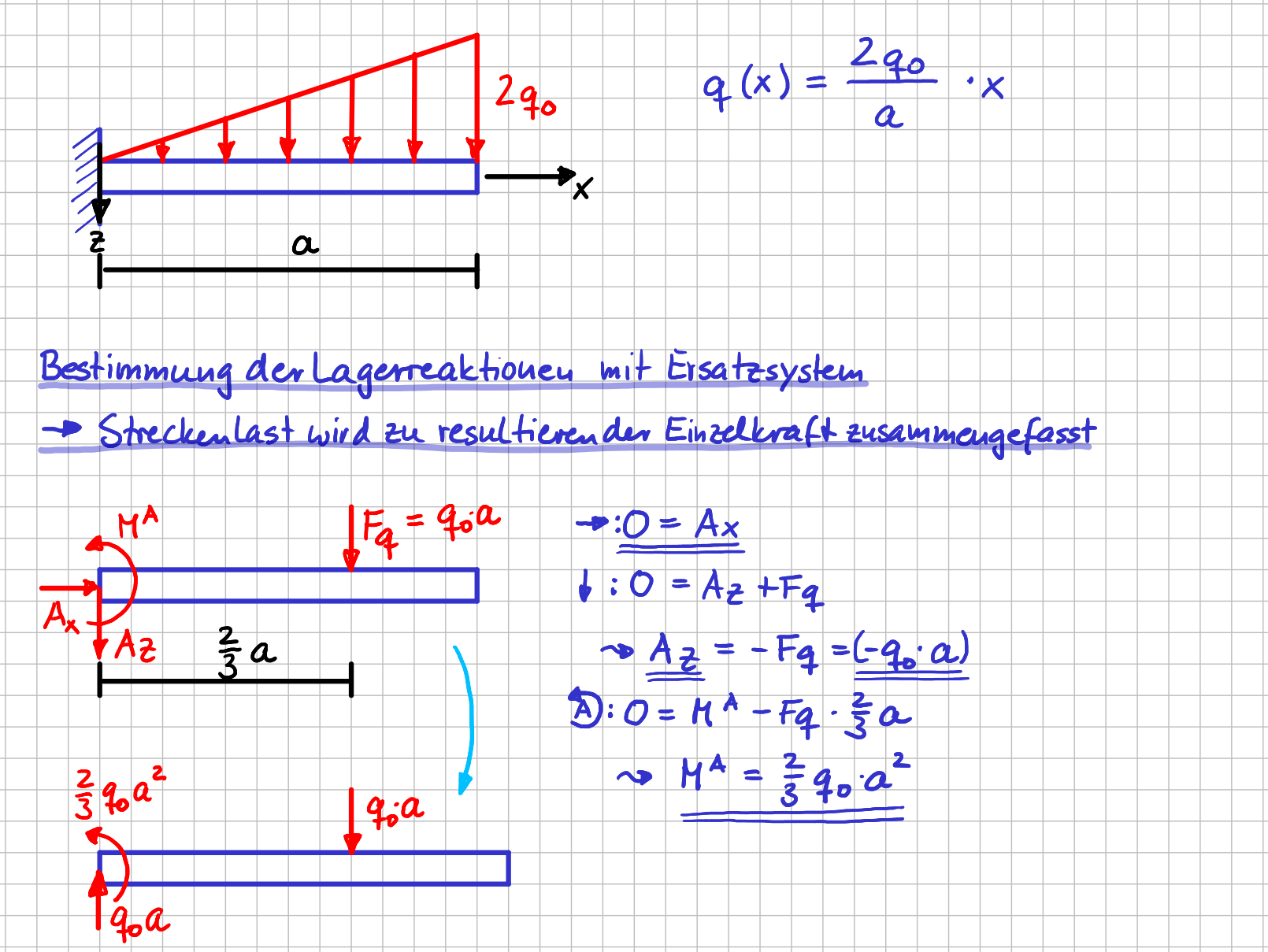
Bestimmung der Lagerreaktionen bei einem Balken mit dreiecksförmiger Streckenlast
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Bestimmung_Lagerreaktionen_dreiecksfoermige_Streckenlast.png
Wenn du jetzt für dieses System die Schnittgrößen bestimmen willst, gehst du ganz ähnlich vor. Allerdings bestimmst du jetzt die resultierende Einzelkraft für das Teil(!)system rechts oder links vom Schnitt. Du führst also als erstes den Schnitt ein und zeichnest ein Freikörperbild des Teilsystems, mit dem du weiter arbeiten möchtest. Für dieses Teilsystem bildest du dann die resultierende Einzelkraft für den Streckenlastanteil, der eben in diesem Teilsystem vorhanden ist.
Wie das konkret geht, siehst du in der folgenden Abbildung.
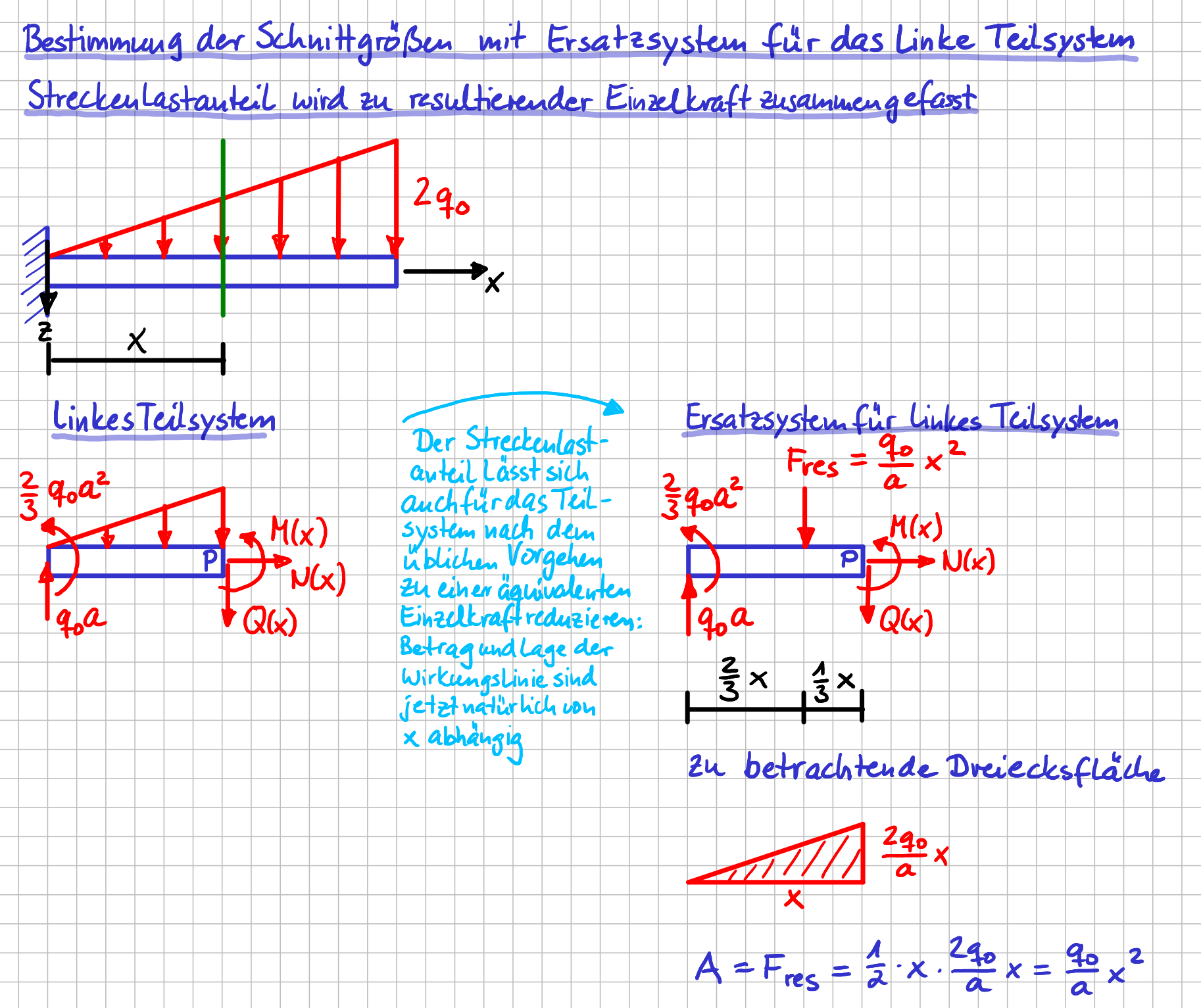
Auf dem Weg zu den Schnittgrößen: Bestimmung der resultierenden Einzelkraft für das linke Teilsystem
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Auf_dem_Weg_zu_den_Schnittgroessen_Einzellast.png
Und für das Ersatzsystem des linken Teilsystems kannst du jetzt wieder 'wie immer' die Gleichgewichtsbedingungen aufstellen und diese dann nach den Schnittgrößen umstellen.
Das sieht dann so aus:
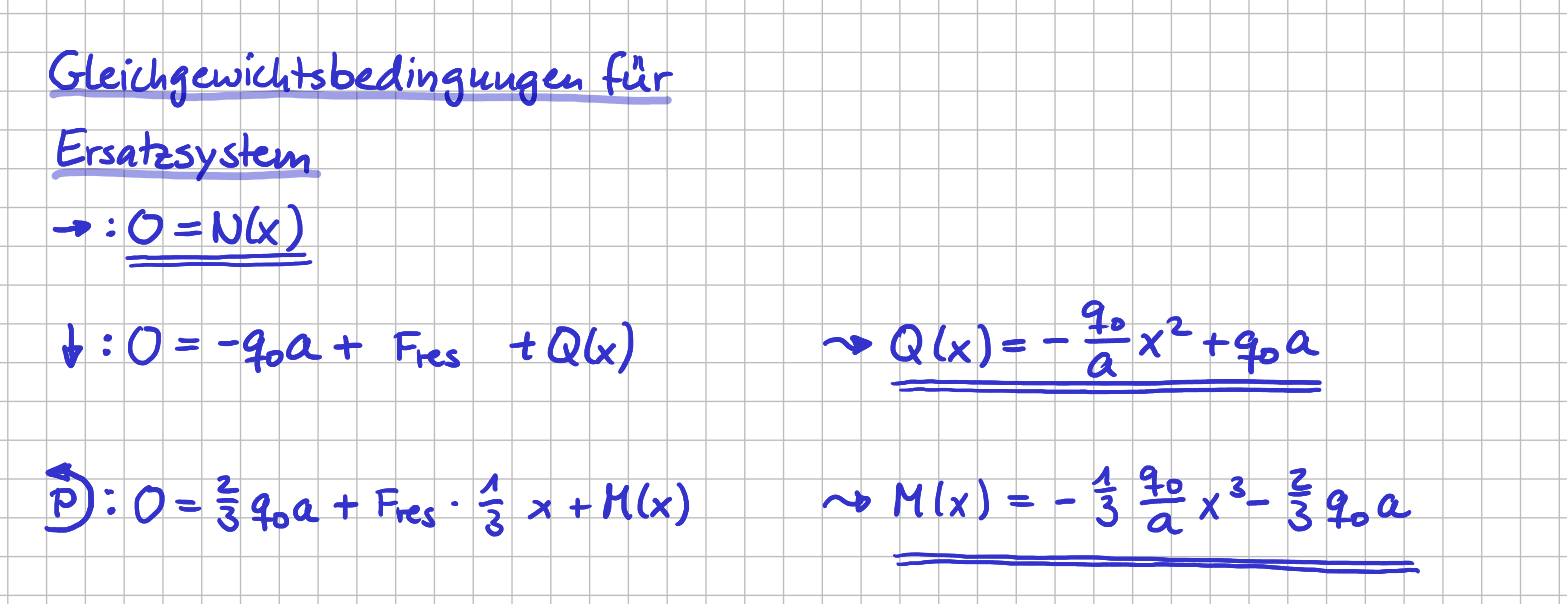
Bestimmung der Schnittgrößen aus den Gleichgewichtsbedingungen des Ersatzsystems
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13825/mod_book/chapter/2217/Bestimmung_der_Schnittgroessen_aus_Ersatzsystem.png
Wenn du dich fragst, warum Schnittgrößen überhaupt ausgerechnet werden? Stell dir vor du hast einen Balken in einem realen System. Der ist irgendwann mal für gewisse Lastfälle ausgelegt worden. Sein Material und seine geometrischen Abmessungen sind also unter der Annahme bestimmter äußerer Belastungen festgelegt worden. Jetzt kommt ein neuer Lastfall hinzu und du möchtest feststellen, ob der Balken immer noch halten würde. Dazu musst du natürlich erstmal wissen, an welcher Stelle die kritischen inneren Größen auftreten. Es gibt Werkstoffe, die besonders empfindlich bei Zugbelastungen sind. Andere Werkstoffe versagen typischer Weise aufgrund von Scherbelastungen, wie sie durch Querkräfte erzeugt werden. Die Bestimmung von Schnittgrößen hat also große praktische Bedeutung. Wie du genau feststellen kannst, ob ein Balken hält oder nicht, lernst du in dem Teilgebiet der Mechanik, dass sich Elastostatik nennt. Hier werden die sich aus den Schnittgrößen ergebenden Spannungen betrachtet und die zugehörigen Deformationen betrachtet.
