Knotenpunktsverfahren

Wie der Name schon verrät, werden beim Knotenpunktsverfahren die Knoten einzeln betrachtet. Wir haben ja bereits gesehen, dass ein Knoten eine der beiden Körperarten ist, die aus einem Fachwerk herausgeschnitten werden kann. Die Knoten werden im ersten Schritt freigeschnitten. Im zweiten Schritt werden die Gleichgewichtsbedingungen für die Knoten aufgestellt.

Dabei gibt es für das konkrete Vorgehen zwei verschiedene Varianten, die ich dir beide jetzt zeigen werde. 

Eine wichtige Bemerkung noch vorab: Der Knoten eines Fachwerks ist im Sinne der Mechanik ein Körper. Und für eine Körper kannst du in der Statik die Gleichgewichtsbedingungen aufstellen. Im ebenen Fall sind das zwei Kräftegleichgewichte und ein Momentengleichgewicht. Der Knoten als Körper ist in sofern besonders, als er keine Ausdehnung hat: Er ist ein Punkt. Für einen Knoten kannst du also nur die Kräftegleichgewichte in zwei Richtungen aufstellen.

Variante 1: Knoten nacheinander im Sinne der Abbrechbarkeit des Fachwerks freischneiden

Auf den Abbildungen findest du Lautsprechersymbole. Durch Anklicken kannst du dir Erläuterungen zu den einzelnen Schritten anhören.

Der Vorteil bei dem Vorgehen "im Sinne der Abbrechbarkeit" ist also, dass du immer maximal zwei Gleichungen hast, die miteinander verkoppelt sind und die du direkt nach den beiden enthaltenen Unbekannten lösen kannst.

Variante 2: Zuerst alle Knoten freischneiden

Du kannst im ersten Schritt auch erst alle Knoten freischneiden und für alle Knoten die Gleichgewichtsbedingungen aufstellen.

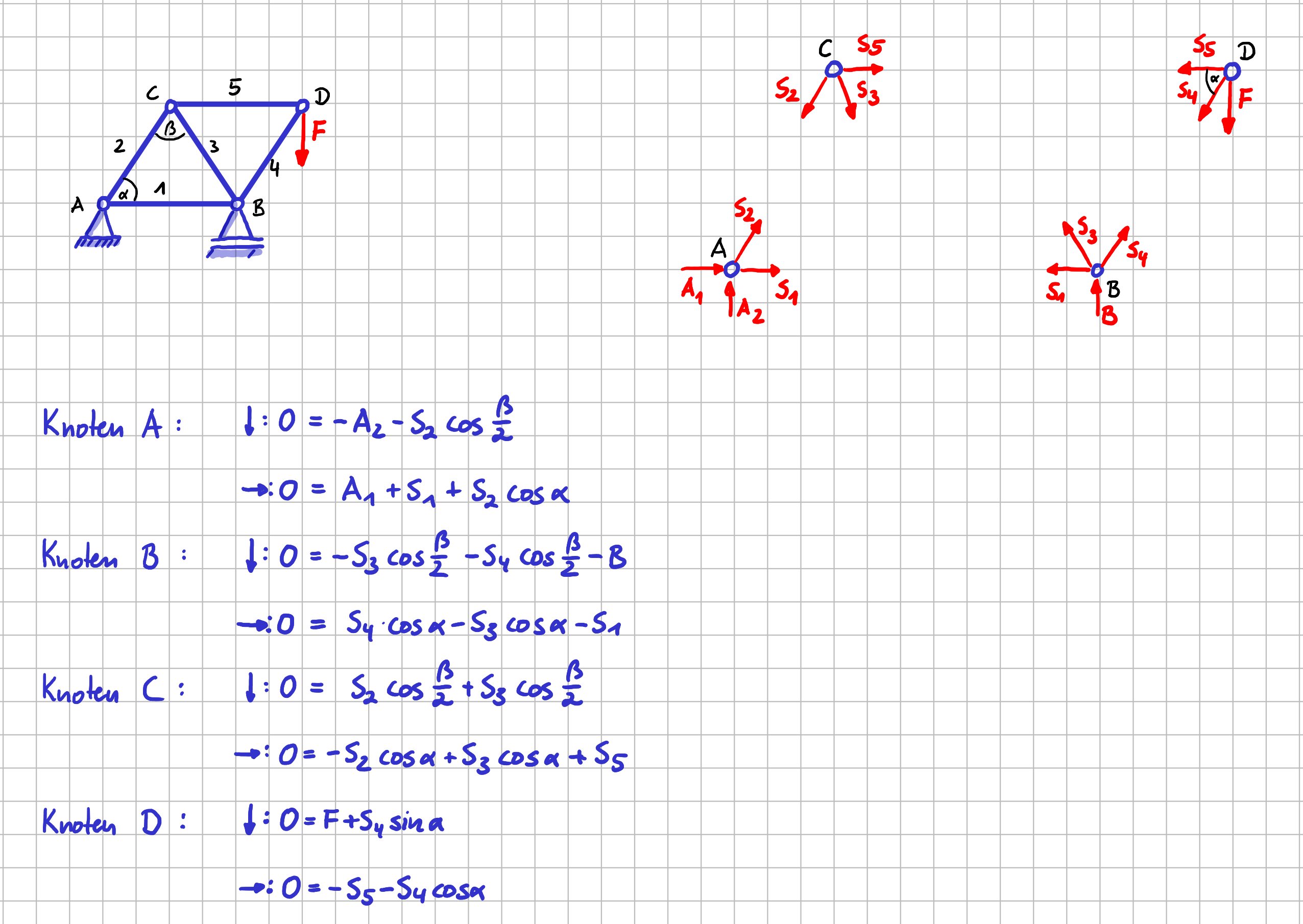
Freikörperbild von allen Knoten und alle Gleichgewichtsbedingungen

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2214/FKB_alle_Knoten_alle_GGB.png

Du kannst dir dann überlegen, ob du die Gleichungen nach und nach nach den gesuchten Unbekannten auflöst. Oder du kannst die Gleichungen in ein lineares Gleichungssystem der Form \( \vec{\vec{A}} \ \vec{x}=\vec{b} \) überführen und mit einem Verfahren für lineare Gleichungssysteme lösen.

Gleichgewichtsbedingungen überführt in ein Gleichungssystem

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2214/GBB_ueberfuehrt_in_Gleichungssystem.png