Fachwerk
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Fachwerk |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 14:01 |
1. Einstieg Fachwerk
Einstieg Fachwerk
Im Kapitel Fachwerk geht
es um Strukturen, die aus Stäben aufgebaut sind. Stäbe sind
Modellkörper, die nur entlang der Stabachse Kräfte übertragen können.
Fachwerke, wie wir sie in der Mechanik betrachten, haben nichts mit den Fachwerken, wie du sie vielleicht von alten Fachwerkhäusern kennst, zu tun. Es geht vielmehr und die Art von Strukturen, wie du sie von einem Baustellenkran oder Brücken kennst.
Wilmas Mechanikwelt
Ausflug an die Elbe.
Endlich Wasser an den Pfoten.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2216/Wilma_Fachwerk_01.png

Auf dem Rückweg.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2216/Wilma_Fachwerk_02.png
2. Das ideale Fachwerk
Das ideale Fachwerk
Das ideale Fachwerk ist eine Modellart, die in der Mechanik häufig zum Einsatz kommt.
Was kennzeichnet ein ideales Fachwerk?
- Es besteht aus Stäben und Knoten.
- Alle Stäbe sind gerade.
- Die Stäbe sind an den Enden in sogenannten Knoten gelenkig miteinander verbunden.
- Die Knoten sind reibungsfreie Gelenke.
- Kräfte greifen nur an den Knotenpunkten an.
Wenn du die Lektion "Lager" schon durchgearbeitet hast, sind reibungsfreie Gelenke schon alte Bekannte für dich. Die Verbindungselemente zwischen den Stäben, die Knoten, sind genau solche Gelenke.
Du hast vielleicht auch schon mal Systeme mit mehreren Körpern betrachtet. Ein Fachwerk ist ein System mit zwei verschiedenen Arten: zum Einen gibt es Körper vom Typ "Stab" und zum anderen gibt es Körper vom Typ "Knoten". Auf diesen Punkt kommen wir ein wenig später beim Freischneiden nochmal zurück.
In der nächsten Abbildung siehst du ein ideales Fachwerk, das aus drei Stäben (\( s=3 \)) und drei Knoten (\( k=3 \)) besteht. Es ist in \( A \) mit einem Festlager und in \( B \) mit einem Loslager gelagert.
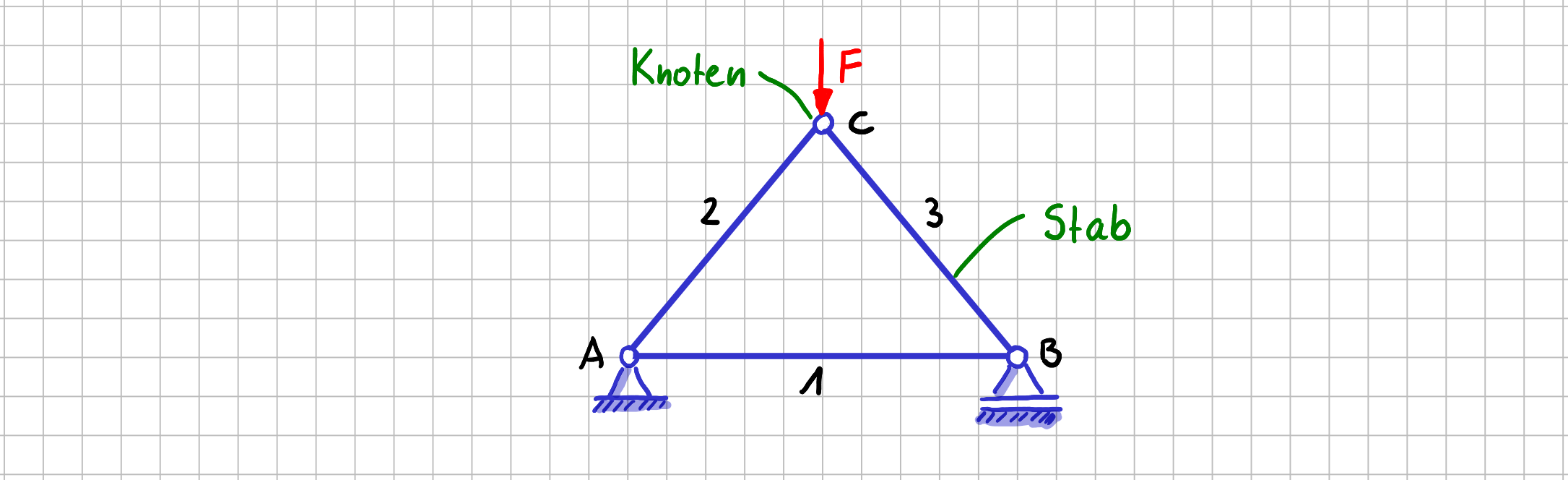
Beispiel für ein "ideales Fachwerk"
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk.png
"Was sind denn die Konsequenzen aus den fünf Annahmen", fragst du dich jetzt vielleicht. Um diese Frage beantworten zu können, mach einfach das, was du inzwischen bestimmt schon ganz oft gemacht hast: Freischneiden und ein Freikörperbild erstellen. Bisher hast du in den meisten Fällen vielleicht nur das System von der Umgebung getrennt, also ein Freikörperbild in dieser Art erstellt:
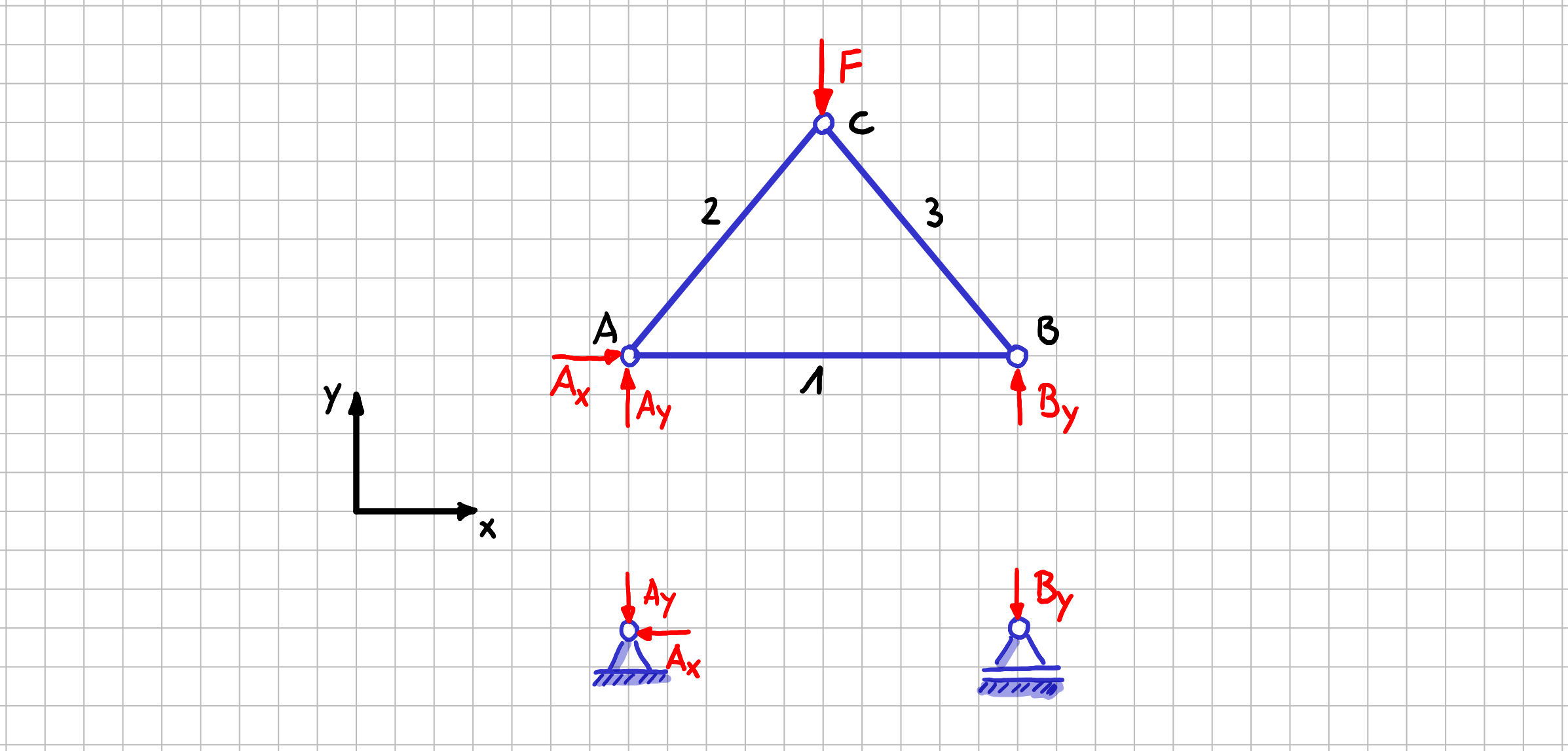
Fachwerk als Ganzes getrennt von der Umgebung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_getrennt_von_Umgebung.png
Hier trennst du jetzt zusätzlich noch alle Körper von einander, schneidest also auch alle Knoten und Stäbe frei. In der nächsten Abbildung sieht du, wie dieser Prozess abläuft, wenn du zuerst Stab 3 freischneidest und dann Knoten C.
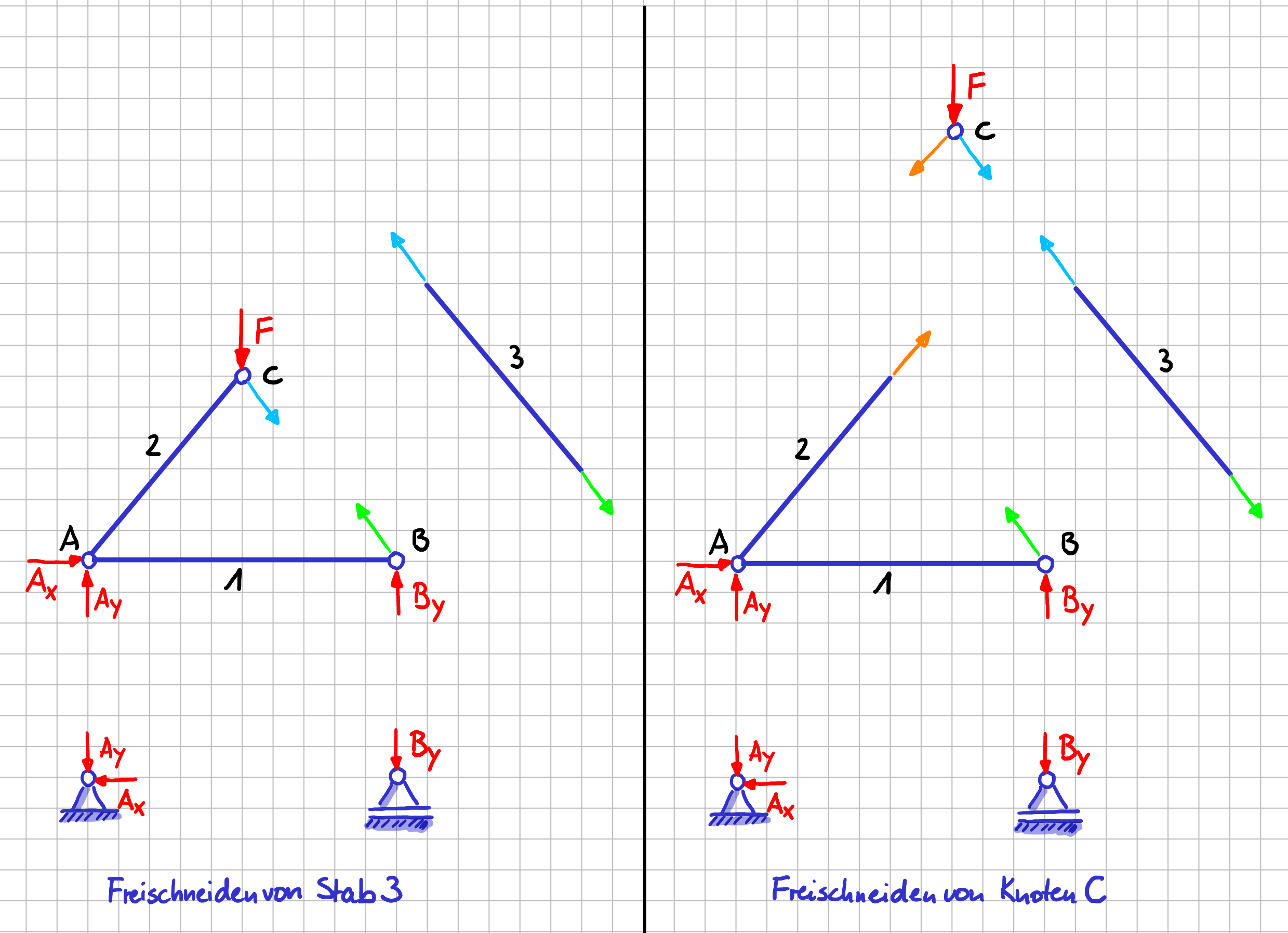
Schrittweises Freischneiden der einzelnen Körper des Fachwerks: Stab 3 (links), Knoten C (rechts)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_schrittweises_Freischneiden.png
Wenn du diesen Prozess fortsetzt, erhältst du am Ende das vollständige Freikörperbild für das Fachwerk, in dem alle Stäbe und Knoten freigeschnitten sind. Das sieht dann so aus:
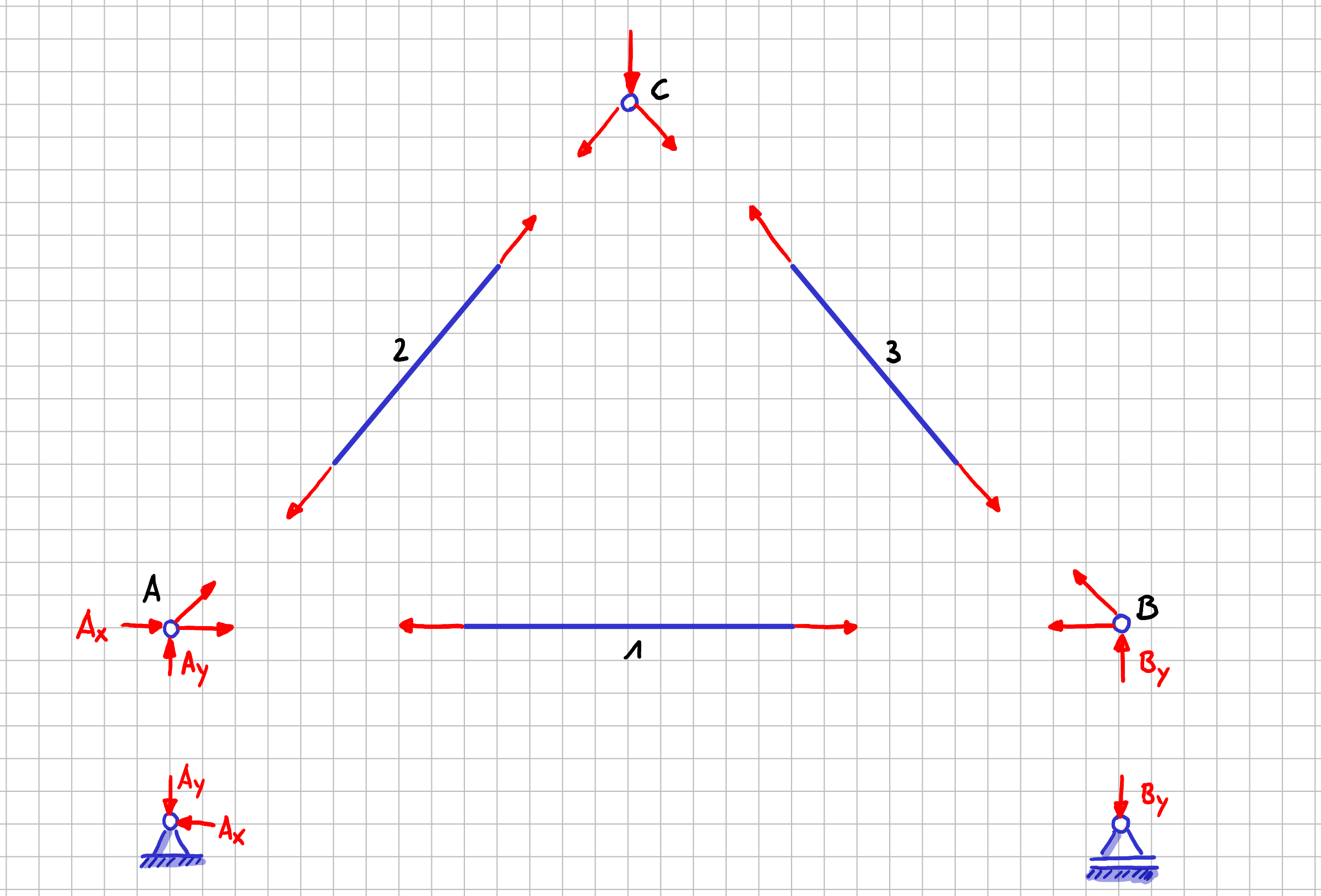
Vollständiges Freikörperbild für das Beispielfachwerk: Alle Stäbe und alle Knoten sind freigeschnitten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_vollstaendiges_FKB.png
Eine gute Frage wäre jetzt, warum in den Freikörperbildern bei den Stäben nur Kräfte in Richtung der Stäbe eingezeichnet sind. Was ist mit Momenten und Kräften quer zur Stabrichtung? \( - \) Wir nehmen ja an, dass die Gelenke reibungsfrei sind. Das erklärt schon mal, warum keine Momente auftauchen. Und die Kräfte quer zur Stabachse, was ist mit denen? Zeichne dir doch einfach mal das Freikörperbild eines Stabes hin, bei dem an beiden Enden nicht nur Kräfte IN Richtung des Stabes, sondern auch SENKRECHT dazu wirken.

Einen Stab mit Kraft senkrecht zur Stabachse kann es nicht geben
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Stab_mit_senkrechter_Kraft.png
Und jetzt stell in Gedanken oder durch Aufschreiben mal das Momentengleichgewicht um den Endpunkt \( A \) auf......tada....und schon siehst du, dass nur die besagte Kraft mal ihrem Hebelarm auftaucht. Und da der Hebelarm nachweislich nicht Null ist, heißt das, dass keine Kraft senkrecht zur Stabrichtung wirken kann.
Bis jetzt ist beim Thema "Fachwerk" also nicht wirklich viel neu. Du hast dir gerade selbst 'nur' mit Kenntnissen über das Freischneiden und das Aufstellen eines Momentengleichgewichts hergeleitet, was ein Stab ist:
Ein Element, was nur Kräfte in Stabrichtung übertragen kann. Das einzige, was du als neue Information brauchtest, waren die Annahmen, von denen du ja auch schon die zum Gelenk kanntest.
Bleibt noch die Frage, wie verhält es sich mit den Kräften in Richtung des Stabes? Du ahnst es vielleicht schon: Stell doch einfach mal ein Kräftegleichgewicht in Stabrichtung auf. Und schwups bekommst du heraus, dass die Kräfte an den Enden eines Stabes denselben Betrag haben und in entgegengesetzte Richtung zeigen.

Kräftegleichgewicht in Stabrichtung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Kraeftegleichgewicht_in_Stabrichtung.png
Wie soll es denn auch anders sein? Es greift ja keine äußere Kraft entlang des Stabes an, und damit auch nicht in Stabrichtung.
Schon erstaunlich, wie weit du mit Freischneiden und Gleichgewichtsbedingungenaufstellen kommst, oder?
In unserem Freikörperbild von vorhin können wir die Kräfte jetzt also auch noch benennen. Üblicherweise wird der Buchstabe \( S \) mit einem Index, der der Nummer des Stabes entspricht, verwendet. Und da wir anhand der Stäbe nicht mehr an Information bekommen, als dass die Stabkräfte an beiden Enden identisch sind, werden die Stäbe üblicher Weise im Freikörperbild gar nicht mit hingezeichnet.
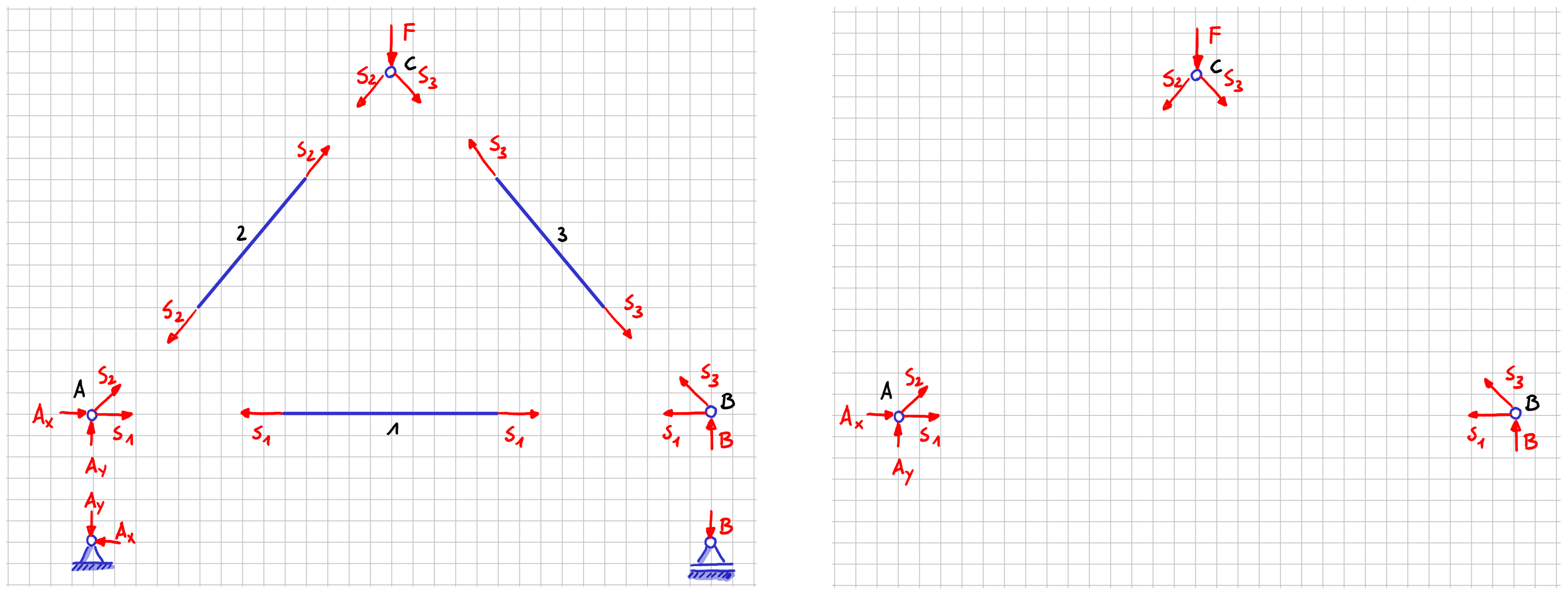
Gesamtfreikörperbild des Fachwerks: mit Stäben (links), ohne Stäbe (rechts)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_mit_ohne_Staebe.png
Aber natürlich wollen wir die Stabkräfte auch wirklich ausrechnen. Darauf konzentrieren wir uns in den kommenden Abschnitten.
Wenn du magst, findest du vorher noch einen Exkurs zum Thema Schnittgrößen beim Stab. Wenn du schauen möchtest, was du noch alles mit dem, was du eh schon kannst, herleiten kannst, schau den Exkurs gerne jetzt an. Ansonsten lohnt es sich den Exkurs auch erst dann anzuschauen, wenn du dich schon mit Schnittgrößen beschäftigt hast ... oder jetzt und später nochmal.
Exkurs zum Thema Gleichgewichtsbedingungen
Du hast jetzt schon soviel vom grundlegenden Handwerkszeug angewendet, da kannst du beim Stab auch einfach noch einen Schritt weitergehen. Du erinnerst vielleicht, dass ein wesentlicher Grundsatz in der Statik der folgende ist: Wenn ein Gesamtsystem im Gleichgewicht ist, ist auch jedes Teilsystem, das daraus herausgeschnitten wird, im Gleichgewicht, so lange geeignete Reaktionsgrößen an der Schnittstelle eingeführt werden. Bei der Betrachtung des ganzen Stabes weiter oben in dieser Lektion, den du aus dem Gesamtfachwerk herausgeschnitten hast, hast du genau dieses Prinzip ja gerade schon angewendet. Sonst hättest du ja gar keine Gleichgewichtsbedingungen aufstellen und die Schlussfolgerungen daraus ziehen können.
Was passiert jetzt aber, wenn du einen Stab selbst noch einmal irgendwo entlang seine Länge auftrennst und anschließend wieder das Kräftegleichgewicht in Stabrichtung aufstellst, dieses Mal eben nur für eines der beiden Teilstücke?
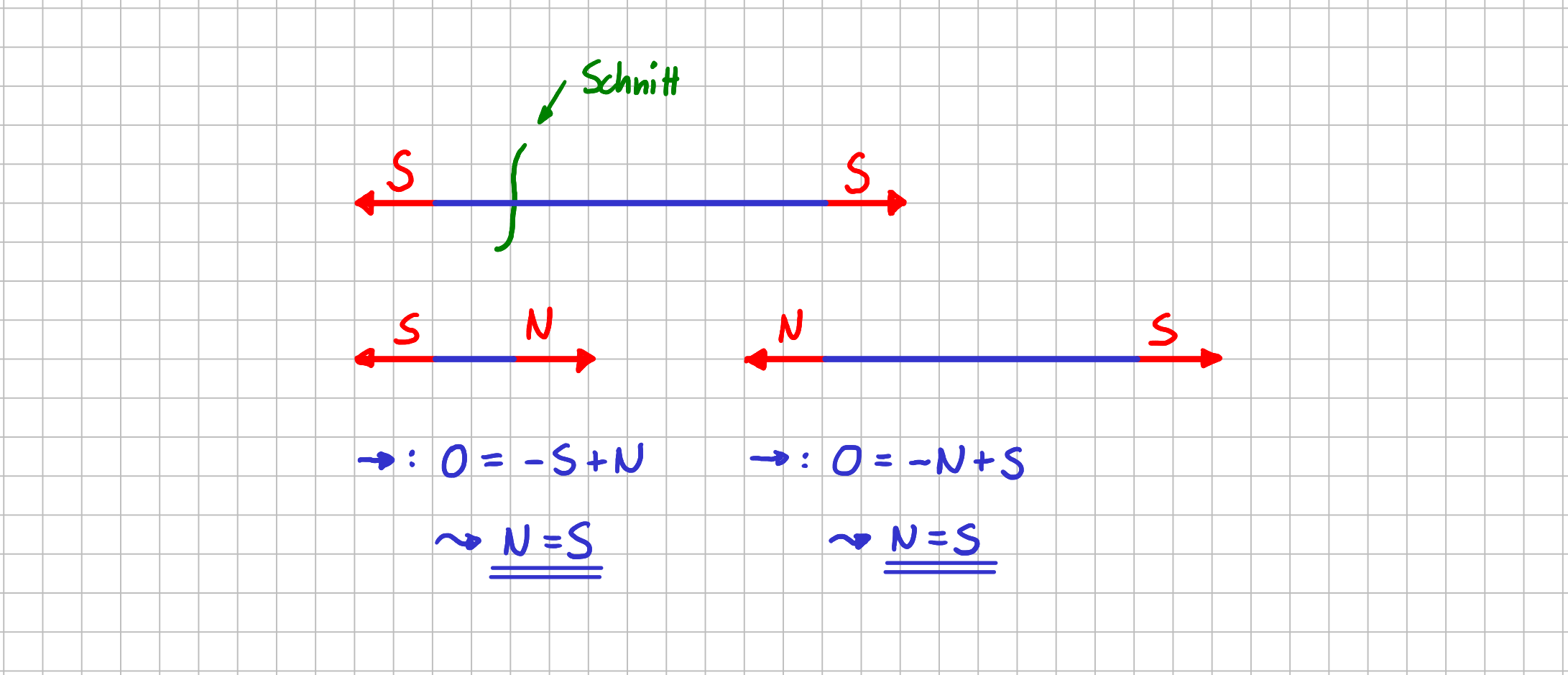
Stab und durchgeschnittener Stab mit innerer Kraft \( N \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Stab_und_durchgeschnittener_Stab.png
Nachdem, was du jetzt schon über Stäbe weißt, kann an der Schnittstelle nur eine Kraft in Richtung des Stabes wirken. Wenn du diese Kraft \( N \) am linken Teilstück des Stabes vom Stab weg einzeichnest, zeigt sie wegen "Actio = Reactio" auch am rechten Teilstück vom Stab weg.
Wenn du für eines der beiden Teilstücke das Kräftegleichgewicht aufstellst, bekommst du heraus, dass die innere Kraft \( N \) vom Betrag her identisch der Kraft \( S \) am Stabende ist. Dabei ist es erwartungsgemäß egal, ob du das linke oder das rechte Teilstück betrachtest.
Damit hast du dir also auch noch selbst hergeleitet, was im Inneren eines Stabes los ist: dort wirkt an jeder Stelle entlang des Stabes dieselbe Kraft. Man nennt sie Normalkraft. Sie ist beim Stab nicht von der Lage der Schnittposition abhängig, sondern entlang des Stabes konstant und hat den Betrag der Stabkraft \( S \).
3. Konventionen
Konventionen
Vielleicht hast du schon mal jemanden sagen hören oder gelesen, dass Stäbe "auf Zug freigeschnitten" werden. In der Tat macht es Sinn festzulegen, in welche Richtung die Stabkräfte beim Freischneiden immer eingezeichnet werden. Mit so einer Konvention im Gepäck lassen sich Stäbe ganz leicht in Bezug auf ihre Belastungsart klassifizieren, wie du gleich sehen wirst.
Es bleiben ja nur zwei Möglichkeiten, die Kräfte beim Stab beim Freischneiden einzuzeichnen: vom Stab weg oder auf den Stab zu.
Wenn du dir noch einmal das Freikörperbild aus dem ersten Abschnitt anschaust, dann siehst du, dass die Kräfte bei den Stäben "von den Stäben weg" eingezeichnet sind. Natürlich muss auch beim Freischneiden der Komponenten eines Fachwerks das Prinzip "Actio = Reactio" gelten. Deshalb zeigen die Stabkräfte auf der Seite der Knoten "vom Knoten weg".
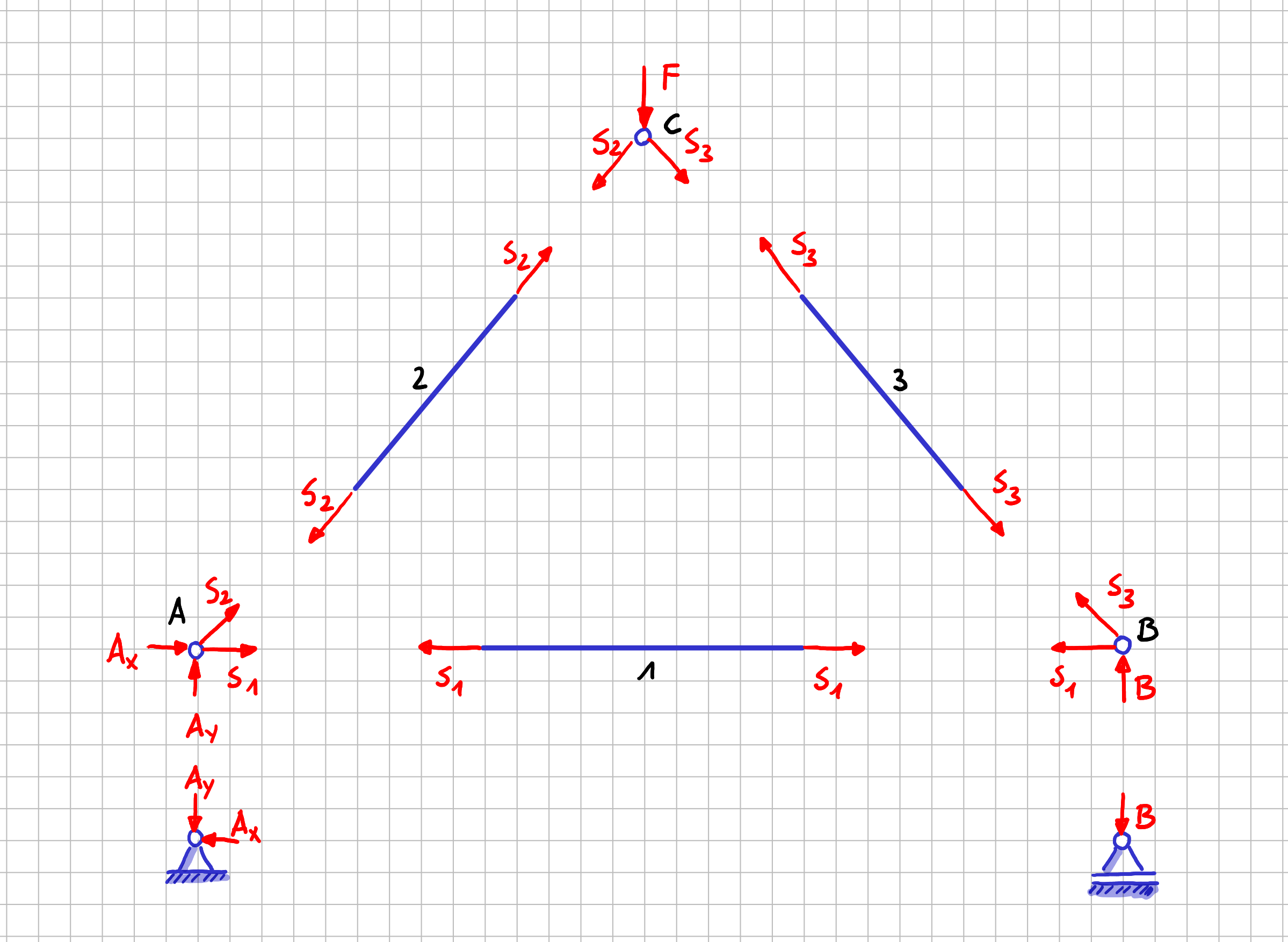
Fachwerk, bei dem die Stäbe "auf Zug" freigeschnitten sind
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2211/Fachwerk_auf_Zug_freigeschnitten.png
Wenn du dir jetzt vorstellst, dass du die eingezeichneten Kräfte auf den Stab mit deinen Händen aufbringst, dann musst du an dem Stab ziehen und nicht etwa drücken, damit die Kräfte in die eingezeichnete Richtung wirken, oder? Deswegen sagt man "Stäbe werden auf Zug freigeschnitten", wenn man die Stabkräfte im Freikörperbild immer vom Stab weg einzeichnet. Wenn du dieser Konvention folgst, dann kannst du die Vorzeichen der Ergebnisse, die du bekommst, wenn du die Stabkräfte tatsächlich ausrechnest, ganz einfach interpretieren. Ein positives Vorzeichen bei einer Stabkraft bedeutet, dass es sich um einen auf Zug belasteten Stab handelt. Der Fachbegriff für so einen Stab ist Zugstab. Umgekehrt ist klar, dass wenn ein negatives Vorzeichen für eine Stabkraft herauskommt, dass es sich um einen Stab handelt, der auf Druck belastet wird. Der Fachbegriff hier ist Druckstab. Und es kann natürlich auch vorkommen, dass in Stäben gar keine Kraft übertragen wird. Diese Stäbe nennt man Nullstäbe.
4. Einfache Fachwerke
Einfache Fachwerke
Vielleicht denkst du: "Das mit den Fachwerken ist ja bisher ganz einfach." Da braucht es doch keinen separaten Abschnitt . Das wäre natürlich schön, wenn dem so wäre, weil du ja bestimmt gemerkt hast, dass du ganz viel Bekanntes (Freischneiden, Gleichgewichtsbedingungen aufstellen und auswerten) 'nur' im Kontext der Modellart "Fachwerk" anwendest.
Der Begriff "Einfaches Fachwerk" ist allerdings in der Tat ein Fachbegriff. Und genauso, wie es einfache Fachwerke gibt, gibt es auch "nichteinfache Fachwerke".
Du wirst sehen, mit einfachen Fachwerken umzugehen und dann auch zu rechnen, also alle Stab- und Lagerkräfte zu bestimmen, ist auch ganz einfach.
Was macht ein Fachwerk denn nun zu einem einfachen Fachwerk?
Es müssen zwei Bedingungen erfüllt sein:
- Für die Anzahl \( s \) der Stäbe und die Anzahl \( k \) der Knoten muss gelten: \( 2k = s + 3 \)
- Das Fachwerk muss abbrechbar sein. Das ist immer dann gegeben, wenn das Fachwerk so aufgebaut werden kann, dass ausgehend von einem Grundstab jeder weitere Knoten durch zwei Stäbe angeschlossen wird, die nicht auf einer Linie liegen. Umgekehrt lässt es sich abbauen oder abbrechen, indem du immer einen Knoten und 'seine' zwei angrenzenden Stäbe entfernst.
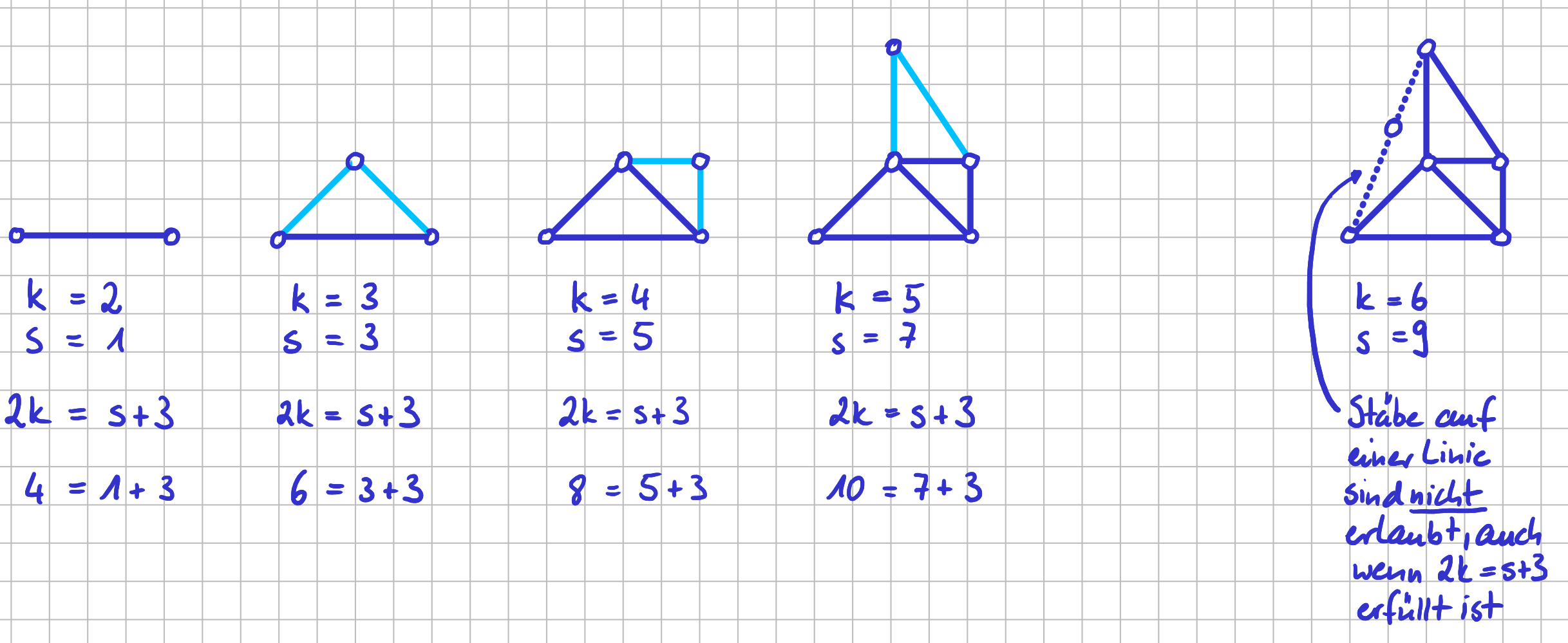
Aufbau eines einfachen Fachwerks: von links nach rechts gedacht; Abbrechen eines einfachen Fachwerks: von rechts nach links gedacht
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2212/Aufbau_eines_einfachen_Fachwerks.png
5. Berechnungsverfahren
Berechnungsverfahren
Bleibt noch die Frage, welche Bedingung erfüllt sein muss, damit sich bei einem einfachen Fachwerk alle Stab- und Lagerkräfte bestimmen lassen.
Wenn ein einfaches Fachwerk als Ganzes statisch und kinematisch bestimmt gelagert ist, lassen sich alle Kräfte mit den Methoden der Statik bestimmen.
Um genau das zu tun, also Stabkräfte zu berechnen, gibt es zwei verschiedene Vorgehensweisen, die getrennt oder auch in Kombination angewendet werden: Das Knotenpunktsverfahren und das Ritterschnitt-Verfahren. Und genau die schauen wir uns jetzt an.
- Knotenpunktsverfahren
- Ritterschnitt-Verfahren
5.1. Knotenpunktsverfahren
Knotenpunktsverfahren
Wie der Name schon verrät, werden beim Knotenpunktsverfahren die Knoten einzeln betrachtet. Wir haben ja bereits gesehen, dass ein Knoten eine der beiden Körperarten ist, die aus einem Fachwerk herausgeschnitten werden kann. Die Knoten werden im ersten Schritt freigeschnitten. Im zweiten Schritt werden die Gleichgewichtsbedingungen für die Knoten aufgestellt.
Dabei gibt es für das konkrete Vorgehen zwei verschiedene Varianten, die ich dir beide jetzt zeigen werde.
Eine wichtige Bemerkung noch vorab: Der Knoten eines Fachwerks ist im Sinne der Mechanik ein Körper. Und für eine Körper kannst du in der Statik die Gleichgewichtsbedingungen aufstellen. Im ebenen Fall sind das zwei Kräftegleichgewichte und ein Momentengleichgewicht. Der Knoten als Körper ist in sofern besonders, als er keine Ausdehnung hat: Er ist ein Punkt. Für einen Knoten kannst du also nur die Kräftegleichgewichte in zwei Richtungen aufstellen.
Variante 1: Knoten nacheinander im Sinne der Abbrechbarkeit des Fachwerks freischneiden
Auf den Abbildungen findest du Lautsprechersymbole. Durch Anklicken kannst du dir Erläuterungen zu den einzelnen Schritten anhören.
Der Vorteil bei dem Vorgehen "im Sinne der Abbrechbarkeit" ist also, dass du immer maximal zwei Gleichungen hast, die miteinander verkoppelt sind und die du direkt nach den beiden enthaltenen Unbekannten lösen kannst.
Variante 2: Zuerst alle Knoten freischneiden
Du kannst im ersten Schritt auch erst alle Knoten freischneiden und für alle Knoten die Gleichgewichtsbedingungen aufstellen.
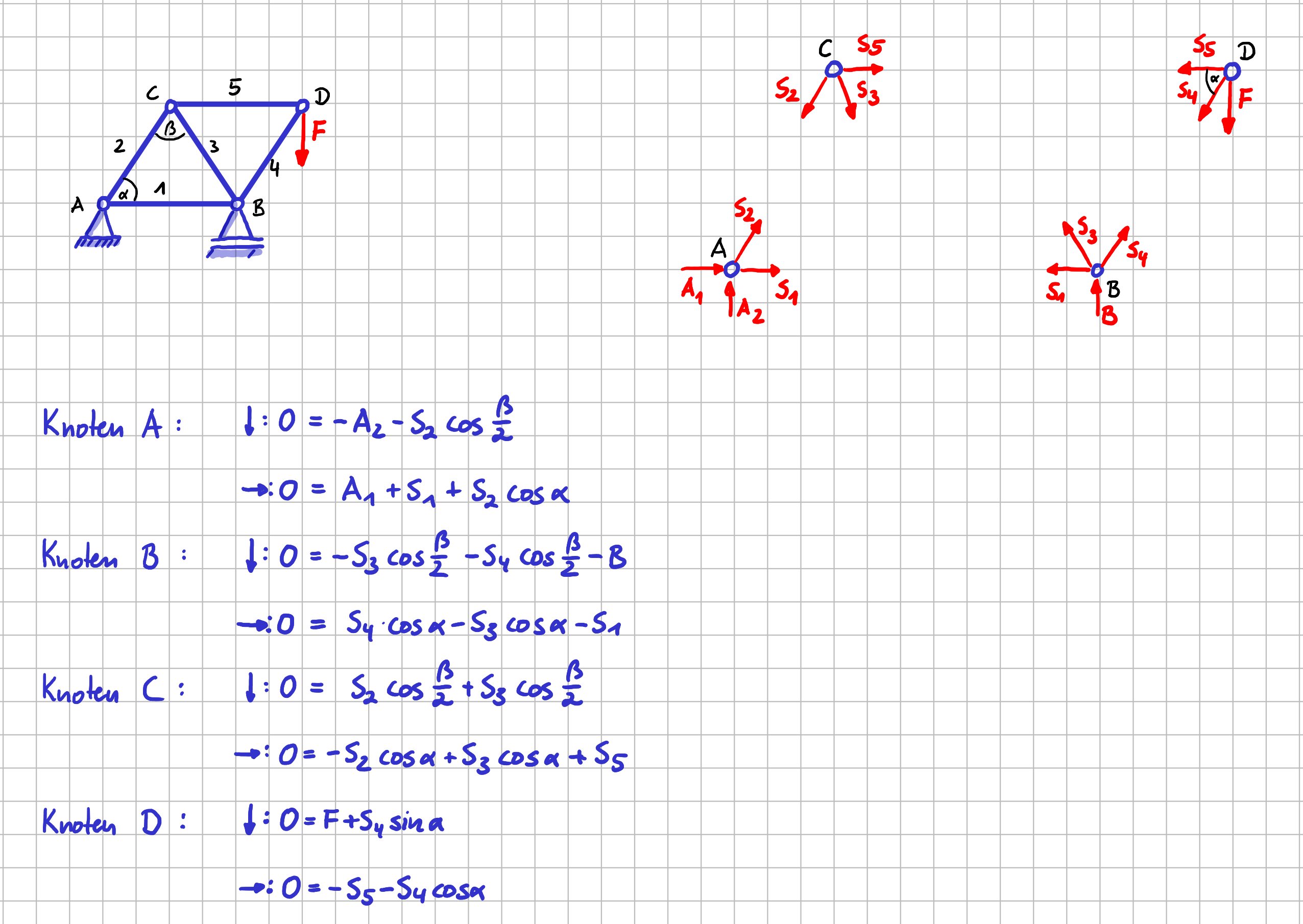
Freikörperbild von allen Knoten und alle Gleichgewichtsbedingungen
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2214/FKB_alle_Knoten_alle_GGB.png
Du kannst dir dann überlegen, ob du die Gleichungen nach und nach nach den gesuchten Unbekannten auflöst. Oder du kannst die Gleichungen in ein lineares Gleichungssystem der Form \( \vec{\vec{A}} \ \vec{x}=\vec{b} \) überführen und mit einem Verfahren für lineare Gleichungssysteme lösen.

Gleichgewichtsbedingungen überführt in ein Gleichungssystem
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2214/GBB_ueberfuehrt_in_Gleichungssystem.png
5.2. Ritterschnitt
Ritterschnitt
Das Ritterschnittverfahren ist nach August Ritter, einem deutschen Mechanikprofessor, der 1908 gestorben ist, benannt. Vielleicht hast du dich auch schon gefragt, ob es nicht möglich ist, einzelne Stabkräfte "in der Mitte eines Fachwerks" zu berechnen, ohne (fast) alle anderen Stabkräfte zu bestimmen. Genau darauf hat August Ritter eine Antwort gefunden: Für gewisse Konstellationen von Stäben in einem Fachwerk, die in der Praxis sehr häufig auftreten, ist genau das möglich. Hierzu schneidest du das Gesamtfachwerk durch einen cleveren Schnitt in zwei Teilfachwerke. Anschließend stellst du die Gleichgewichtsbedingungen für ein Teilfachwerk auf und die Kräfte in den geschnittenen Stäben können direkt bestimmt werden.
"Was genau ist denn ein cleverer Schnitt?", fragst du jetzt? Ein Schnitt, bei dem genau drei Stäbe geschnitten werden, von denen zwei parallel verlaufen und der dritte Knoten der anderen beiden "diagonal" verbindet.
Das ist dir alles viel zu abstrakt? Kein Problem. Dann schauen wir uns das Ganze doch einfach ganz konkret an einem Beispiel an. Klick auf das Lautsprechersymbol, um dir die Erläuterungen zu den einzelnen Schritten anzuhören.
6. FAQs
FAQs
Zum Ende dieser Lektion findest du noch fünf Fragen, von denen ich ehrlich gesagt hoffe, dass du sie dir beim Bearbeiten der bisherigen Lektion schon gestellt hast. Wenn nicht, auch nicht schlimm. Dann hoffe ich, dass du einen Aha-Effekt hast, wenn du die folgenden Fragen und Antworten durcharbeitest.
1. Warum berechnen wir denn nicht auch beim Knotenpunktsverfahren als erstes die Lagerreaktionen?
Das ist eine sehr gute Frage. Ich habe es bei der Betrachtung des Fachwerks mit dem Knotenpunktsverfahren bewusst nicht getan, um zu zeigen, dass du direkt mit dem Knotenpunktsverfahren auch die Lagerreaktionen berechnen kannst. Natürlich heißt das nicht, dass du immer so vorgehen musst. Ganz im Gegenteil. Na klar kannst du auch bei einem Fachwerk als erstes die Lagerreaktionen berechnen, wenn du anschließend mit dem Knotenpunktsverfahren arbeiten willst, um Stabkräfte zu berechnen. Erlaubt ist alles, was dich deinem Ziel näher bringt. Logisch.
2. Kann ich nur entweder das Knotenpunktsverfahren oder den Ritterschnitt anwenden?
Du kannst natürlich auch beide Verfahren kombinieren. Du beachtest ja bei beiden Verfahren die grundlegenden Gesetze der Statik. Also: Sammle deine Erfahrungen und entscheide von Mal zu Mal neu, welches Verfahren du wann anwendest. Ich finde es immer beruhigend zu wissen, dass das Knotenpunktsverfahren für einfache Fachwerke immer funktioniert, um alle Lager- und Stabkräfte ausrechnen zu können. Richtig Spaß macht es aber erst, wenn ich einen Weg finde, der effizient und deshalb clever ist. Wenn du in einem ersten Schritt schon einige Kräfte per Ritterschnitt bestimmen kannst, ist das doch super. Dann wird es anschließend beim Knotenpunktsverfahren umso einfacher, weil du schon weniger Unbekannte übrig hast.
3. In Büchern oder anderen Informationsquellen gibt es immer auch einen Abschnitt über Nullstäbe. Warum gibt es den denn hier nicht?
Das ist gut beobaachtet, dass es diesen Abschnitt sonst eigentlich immer gibt. Aber mal ehrlich: brauchst du den wirklich? Ist es nicht viel cooler, dass du inzwischen weißt, wie du Nullstäbe finden kannst (ohne wirklich irgendwas auswendig zu lernen oder dir zusätzlich merken zu müssen)?
Schau dir das folgende Fachwerk an.
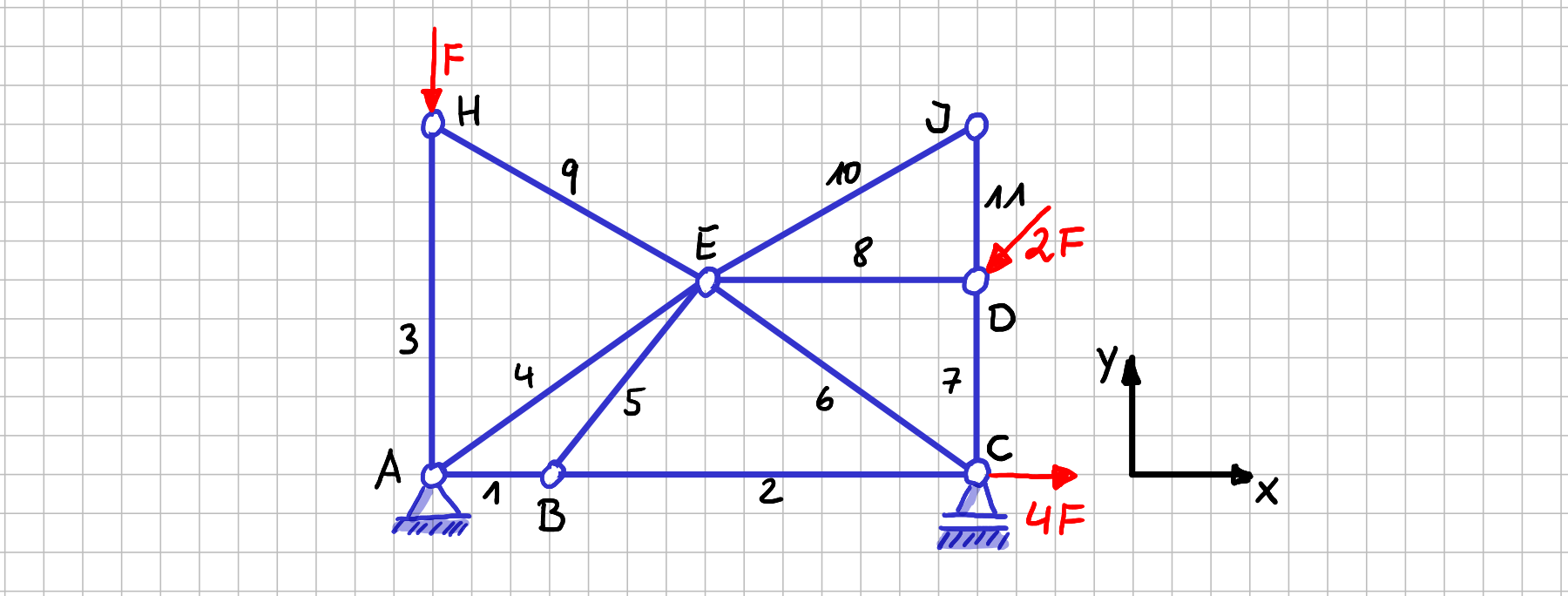
Beispielfachwerk zur Bestimmung von Nullstäben
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Beispielfachwerk_Nullstaebe.png
Wenn du offensichtliche Nullstäbe suchst, schaust du dir vorab Knoten einzeln an, schneidest sie also (gedanklich) aus dem System heraus. Bei welchen Knoten würdest du anfangen, nach offensichtlichen Nullstäben zu schauen? Bestimmt nicht bei Knoten \( E \), oder? Da ist ganz schön was los, da dort sechs Stäbe zusammentreffen. Auch nicht bei Knoten\( A \), da dort zwei Lagerkräfte und drei Stabkräfte als Unbekannte in den Gleichgewichtsbedingungen auftauchen. Für jeden Knoten kannst du ja nur die beiden Kräftegleichgewichte aufstellen. Also brauchst du Knoten, in deren Gleichgewichtsbedingungen maximal zwei Unbekannte auftreten. Du brauchst also Knoten, bei denen "wenig los" ist. Das ist z.B. bei Knoten \( J \)der Fall.
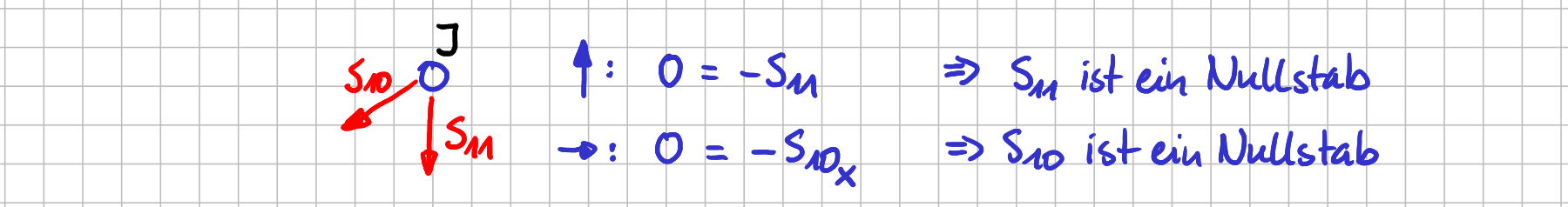
Freikörperbild von Knoten \( J \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_J.png
Die Stabkraft \( S_{11} \) greift an Knoten \( J \) als einzige Kraft in \( y \)-Richtung an. Stab 11 muss also ein Nullstab sein. Das sieht du auch sofort, wenn du für Knoten \( J \) das Kräftegleichgewicht in \( y \)-Richtung aufstellst. Und in \( x \)-Richtung ist \( S_{10} \) die einzige Kraft, die in diese Richtung eine Komponente hat. Also ist auch Stab 10 ein Nullstab. War doch ganz einfach, oder? Du hast nichts anderes getan, als freizuschneiden und hinzuschauen bzw. ein Kräftegleichgewicht aufzustellen. Und schon hast du Nullstäbe gefunden. Bei Knoten \( H \) ist auch wenig los.
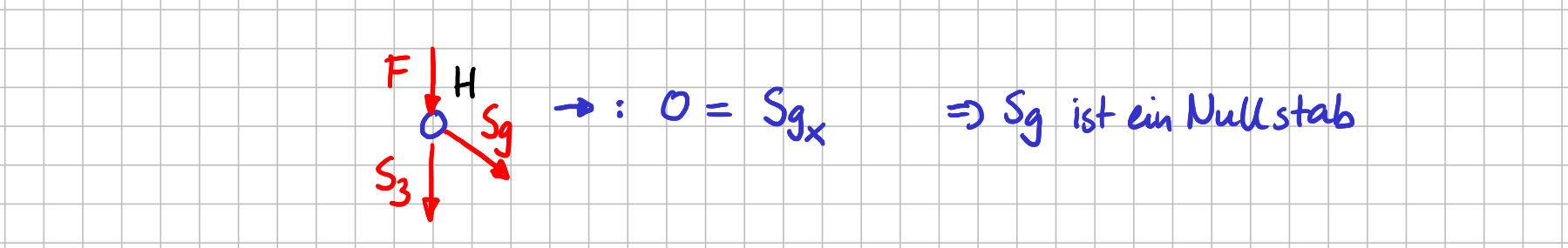
Freikörperbild von Knoten \( H \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_H.png
Hier siehst du im Kräftegleichgewicht in \( x \)-Richtung sofort, dass Stab 9 ein Nullstab ist, da die Kraft \( S_9 \) die einzige Kraft mit einer Komponente in \( x \)-Richtung ist. Und mit exakt denselben Argumenten findest du bei Knoten \( B \) heraus, dass Stab 5 ein Nullstab ist.
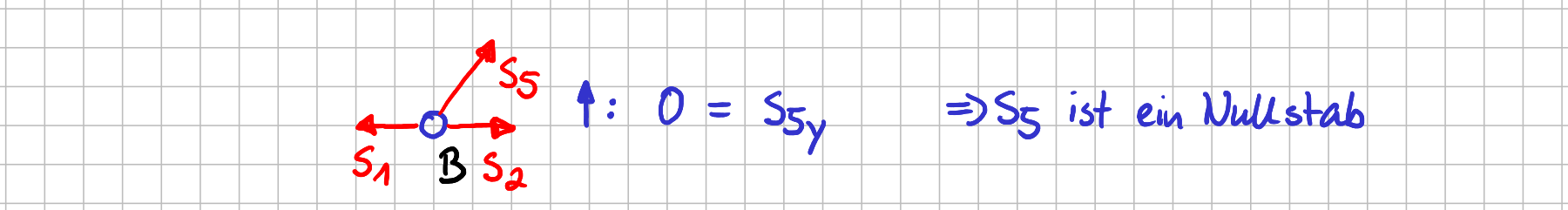
Freikörperbild von Knoten \( B \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_B.png
Hier ist es die Kraft \( S_5 \), die als einziges eine Komponente in \( y \)-Richtung hat.
Na gut, jetzt hast du doch noch einen Abschnitt über Nullstbe bekommen. Aber ich hoffe sehr, dass du siehst, dass es sich nicht lohnt, dir zu merken, was eine "unbelastete Ecke" ist oder in welchem Winkel irgendwelche Stäbe oder Kräfte zueinander stehen müssen, damit ein Stab ein Nullstab ist. Suche einfach nach Knoten, an den wenig los ist (= maximal zwei Unbekannte in den Gleichgewichtsbedingungen auftreten) und dann zeichnest du eben das Freikörperbild auf und schon siehst du, was los ist.
Am Ende dieser Seite findest du ganz viele Fachwerke, bei denen du üben kannst, die Nullstäbe zu finden.
4. Eine Kraft kann man in der Statik immer entlang Wirkungslinie verschieben, oder?
Das "immer" in diesem Satz ist nicht richtig. Schau dir das folgende Fachwerk an. Du siehst zwei Mal die gleiche Aufgabe. Der einzige Unterschied ist der Angriffspunkt der Kraft \( F \).
Eine Kraft kann entlang ihrer Wirkungslinie verschoben werden, solange die Wechselwirkung zwischen dem Gesamtsystem und der Umgebung betrachtet wird. Also immer, wenn du Lagerreaktionen berechnest, kannst du Kräfte entlang ihrer Wirkungslinie verschieben. An den Lagerreaktionen verändert sich dadurch nichts.
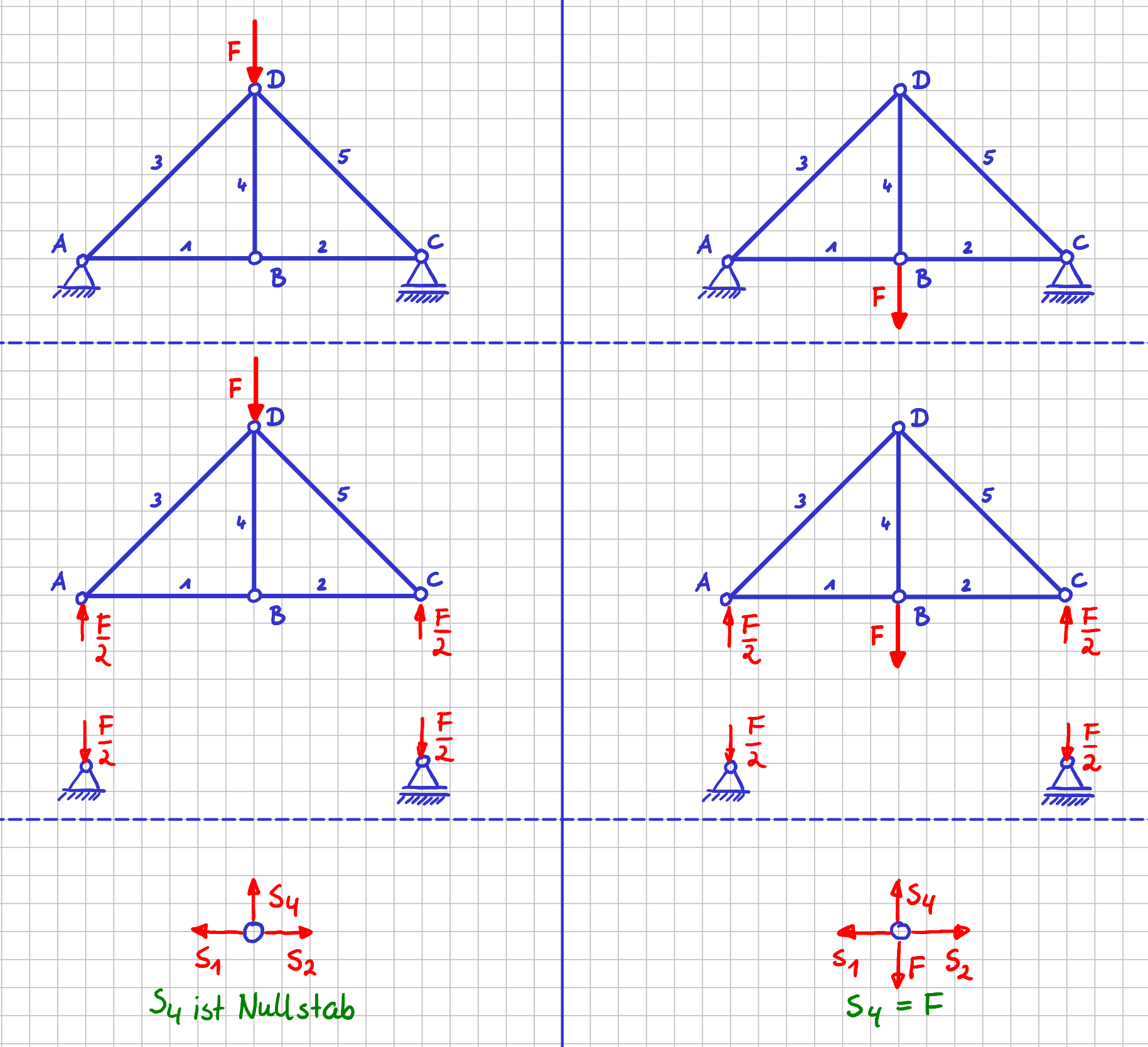
Veranschaulichung, wann eine Kraft entlang ihrer Wirkungslinie verschoben werden kann, und wann nicht
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Veranschaulichung_wann_Kraft_nicht_entlang_Wirkungslinie_verschieben.png
Wenn du aber ins Innere des Systems hineingehst, und das tust du ja, wenn du die Einzelkomponenten eines Systems betrachtest (hier beim Fachwerk sind das die Stäbe bzw. die Knoten), dann spielt es natürlich sehr wohl eine Rolle, wo die Kräfte angreifen. Im linken Fall ist Stab 4 ein Nullstab. Im rechten Fall ist der Betrag der Stabkraft gerade \( F \) .
5. Und was ist mit nichteinfachen Fachwerken?
Ein Fachwerk ist immer dann nichteinfach, wenn eine oder beide Bedingungen, die für einfache Fachwerke gelten müssen, verletzt sind. Heißt das automatisch, dass du dann gar nichts mehr berechnen kannst? Es kommt darauf an.
In der folgenden Abbildung siehst du ein nichteinfaches Fachwerk.
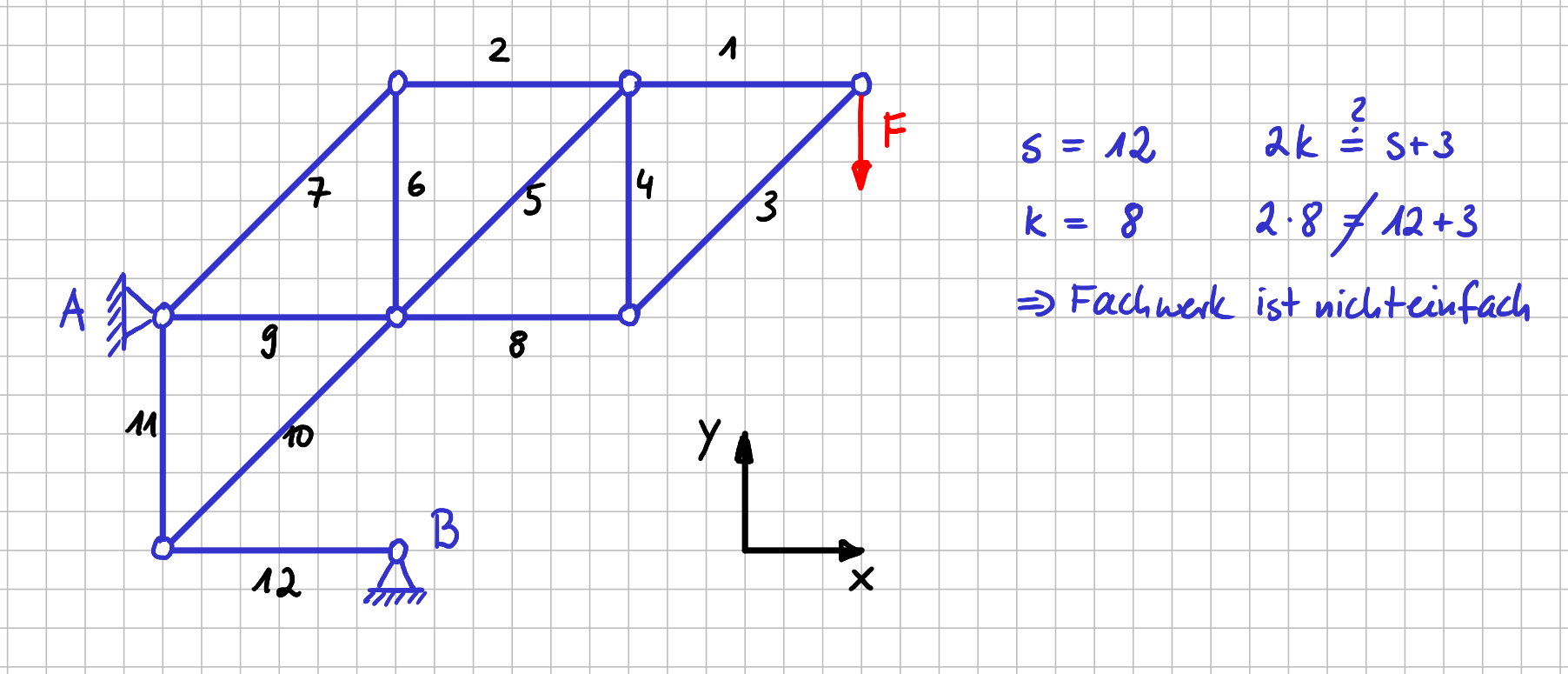
Beispiel für ein nichteinfaches Fachwerk
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Beispiel_nichteinfaches_Fachwerk.png
Und trotzdem kannst du in diesem Fall alle Lagerreaktionen und Stabkräfte berechnen. Warum? Weil am Festlager in Punkt \( B \) nur ein Stab in \( x \)-Richtung angreift, ist klar, dass die \( x \)-Komponoente der Reaktionskraft in Punkt \( B \), also \( B_y \) gleich Null sein muss. Außerdem ist \( B_x=S_{12} \).
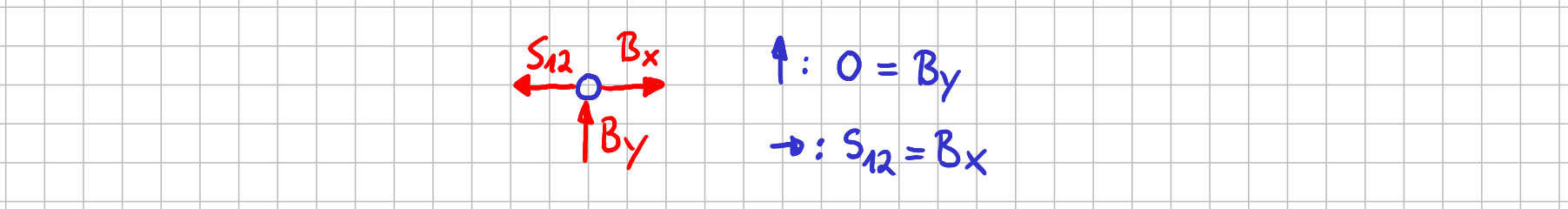
Freikörperbild Knoten \( B \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_B_2.png
Mit diesen Informationen kannst du in einem ersten Schritt also das Festlager in Punkt \( B \) durch ein geeignet ausgerichtetes Loslager ersetzen. Und in einem zweiten Schritt kannst du Stab 12 entfernen und das Loslager nach links verschieben. Dann hast du es wieder mit einem einfachen Fachwerk zu tun.
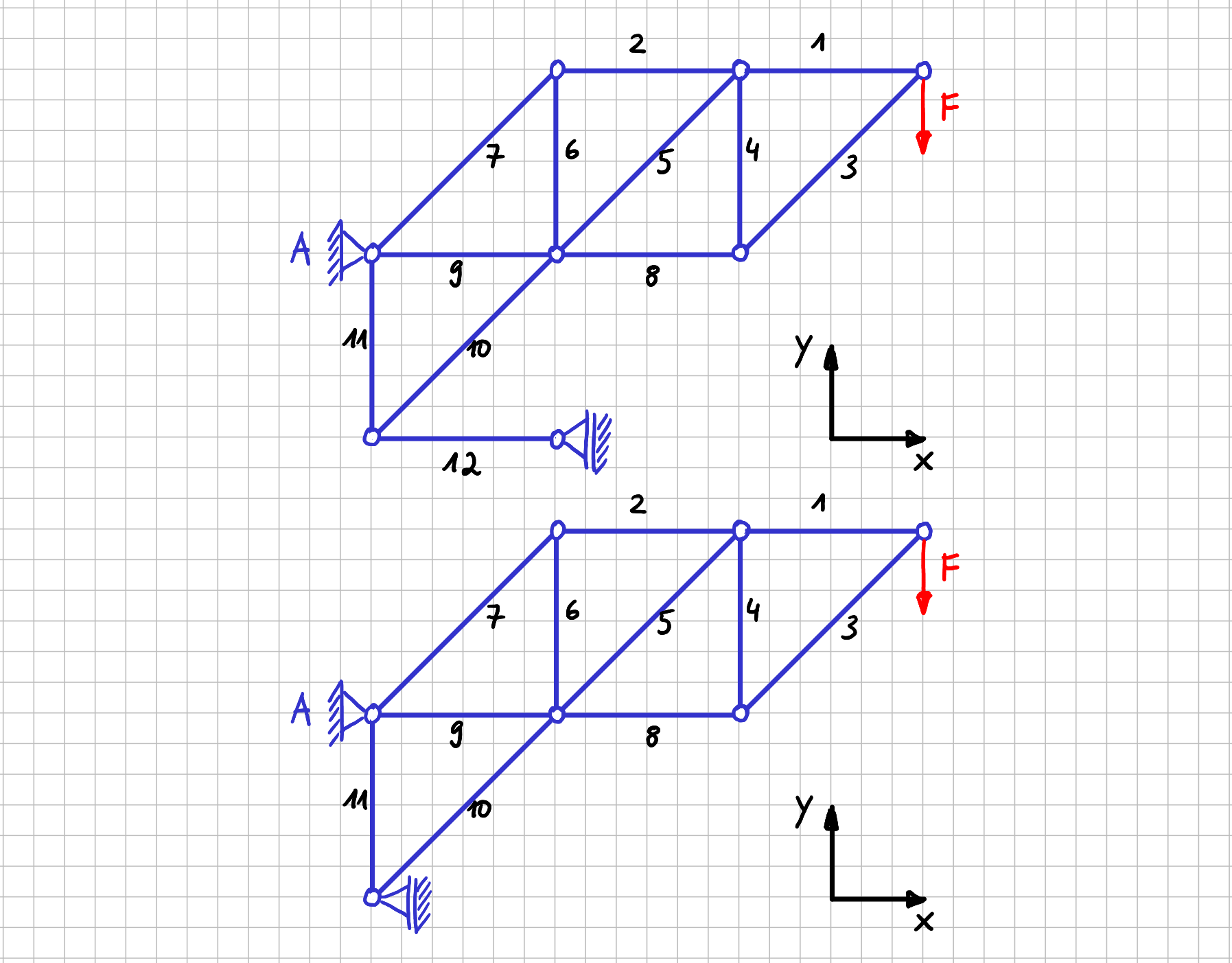
Umbau des Fachwerks unter Berücksichtigung der Erkenntnisse aus der Betrachtung von Knoten \( B \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Umbau_des_Fachwerks.png
Es lohnt sich also, auch bei nichteinfachen Fachwerken genau hinzuschauen.
