Das ideale Fachwerk

Das ideale Fachwerk ist eine Modellart, die in der Mechanik häufig zum Einsatz kommt. 

Was kennzeichnet ein ideales Fachwerk?

1. Es besteht aus Stäben und Knoten.
2. Alle Stäbe sind gerade.
3. Die Stäbe sind an den Enden in sogenannten Knoten gelenkig miteinander verbunden. 
4. Die Knoten sind reibungsfreie Gelenke.
5. Kräfte greifen nur an den Knotenpunkten an.

Wenn du die Lektion "Lager" schon durchgearbeitet hast, sind reibungsfreie Gelenke schon alte Bekannte für dich. Die Verbindungselemente zwischen den Stäben, die Knoten, sind genau solche Gelenke.

Du hast vielleicht auch schon mal Systeme mit mehreren Körpern betrachtet. Ein Fachwerk ist ein System mit zwei verschiedenen Arten: zum Einen gibt es Körper vom Typ "Stab" und zum anderen gibt es Körper vom Typ "Knoten". Auf diesen Punkt kommen wir ein wenig später beim Freischneiden nochmal zurück.

In der nächsten Abbildung siehst du ein ideales Fachwerk, das aus drei Stäben (\( s=3 \)) und drei Knoten (\( k=3 \)) besteht. Es ist in \( A \) mit einem Festlager und in \( B \) mit einem Loslager gelagert.

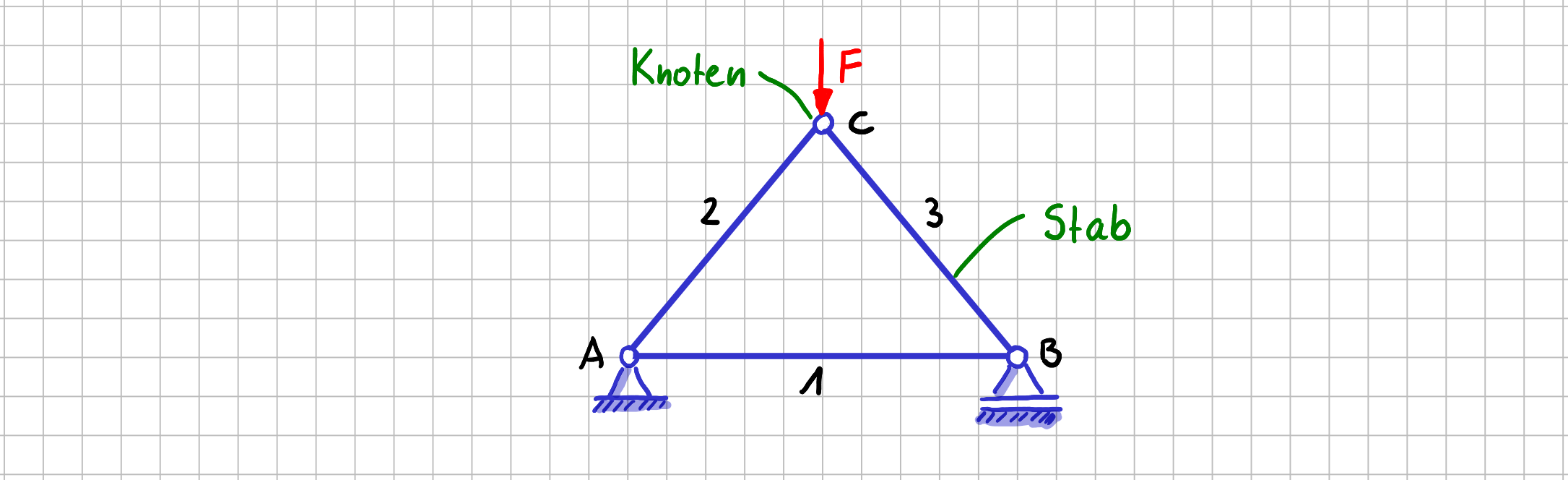
Beispiel für ein "ideales Fachwerk"

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk.png

"Was sind denn die Konsequenzen aus den fünf Annahmen", fragst du dich jetzt vielleicht. Um diese Frage beantworten zu können, mach einfach das, was du inzwischen bestimmt schon ganz oft gemacht hast: Freischneiden und ein Freikörperbild erstellen. Bisher hast du in den meisten Fällen vielleicht nur das System von der Umgebung getrennt, also ein Freikörperbild in dieser Art erstellt:

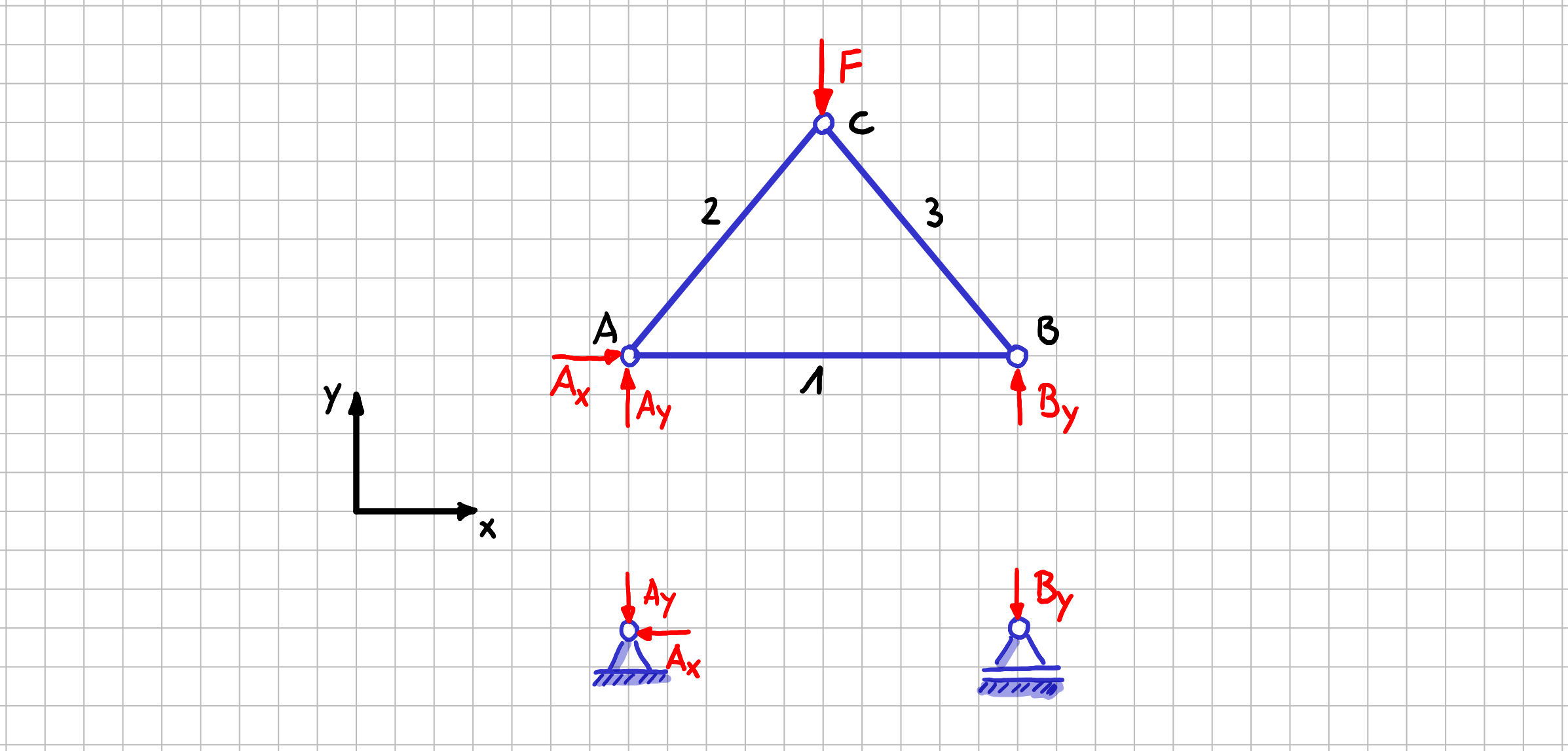
Fachwerk als Ganzes getrennt von der Umgebung

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_getrennt_von_Umgebung.png

Hier trennst du jetzt zusätzlich noch alle Körper von einander, schneidest also auch alle Knoten und Stäbe frei. In der nächsten Abbildung sieht du, wie dieser Prozess abläuft, wenn du zuerst Stab 3 freischneidest und dann Knoten C. 

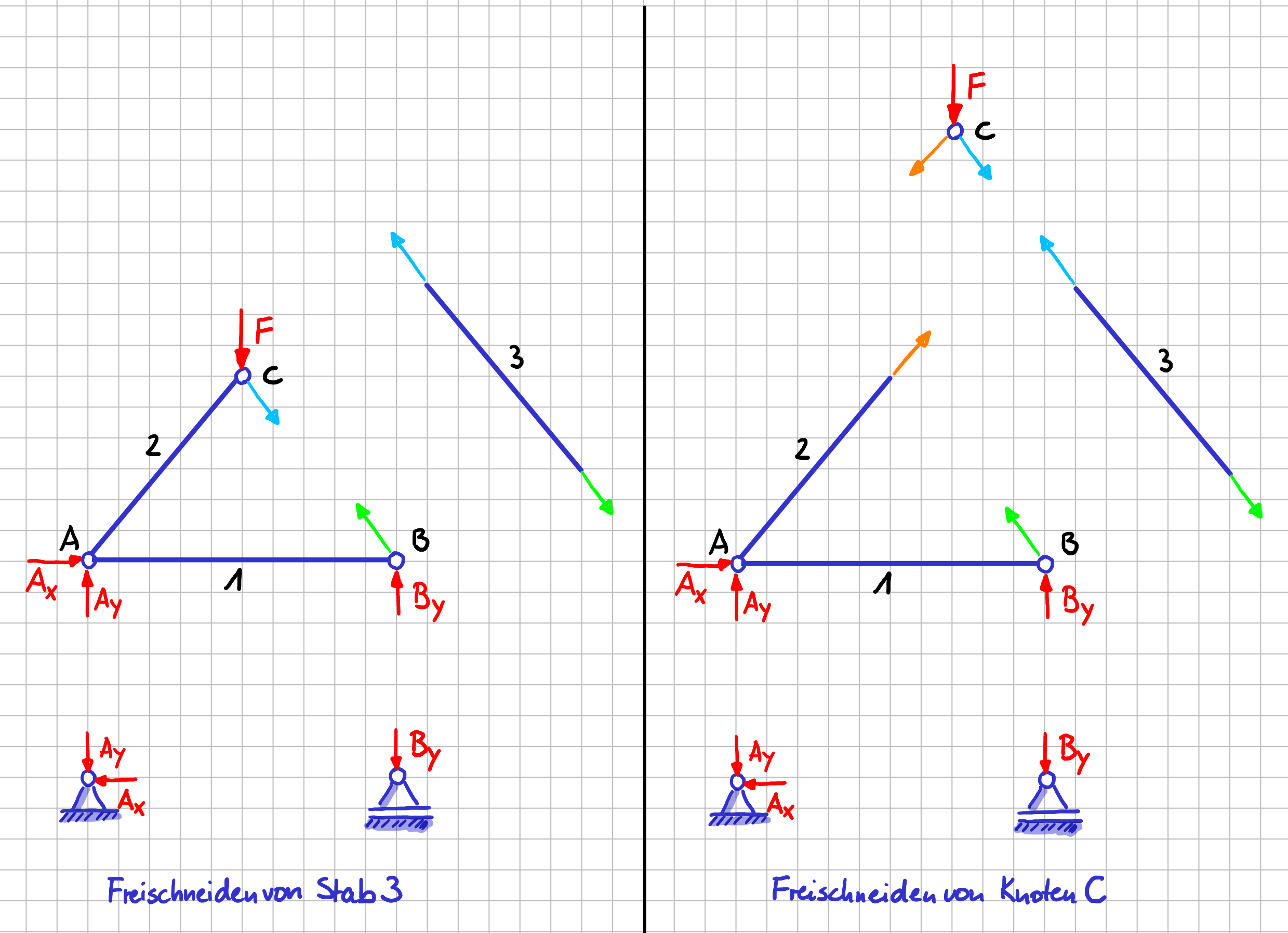
Schrittweises Freischneiden der einzelnen Körper des Fachwerks: Stab 3 (links), Knoten C (rechts)

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_schrittweises_Freischneiden.png

Wenn du diesen Prozess fortsetzt, erhältst du am Ende das vollständige Freikörperbild für das Fachwerk, in dem alle Stäbe und Knoten freigeschnitten sind. Das sieht dann so aus:

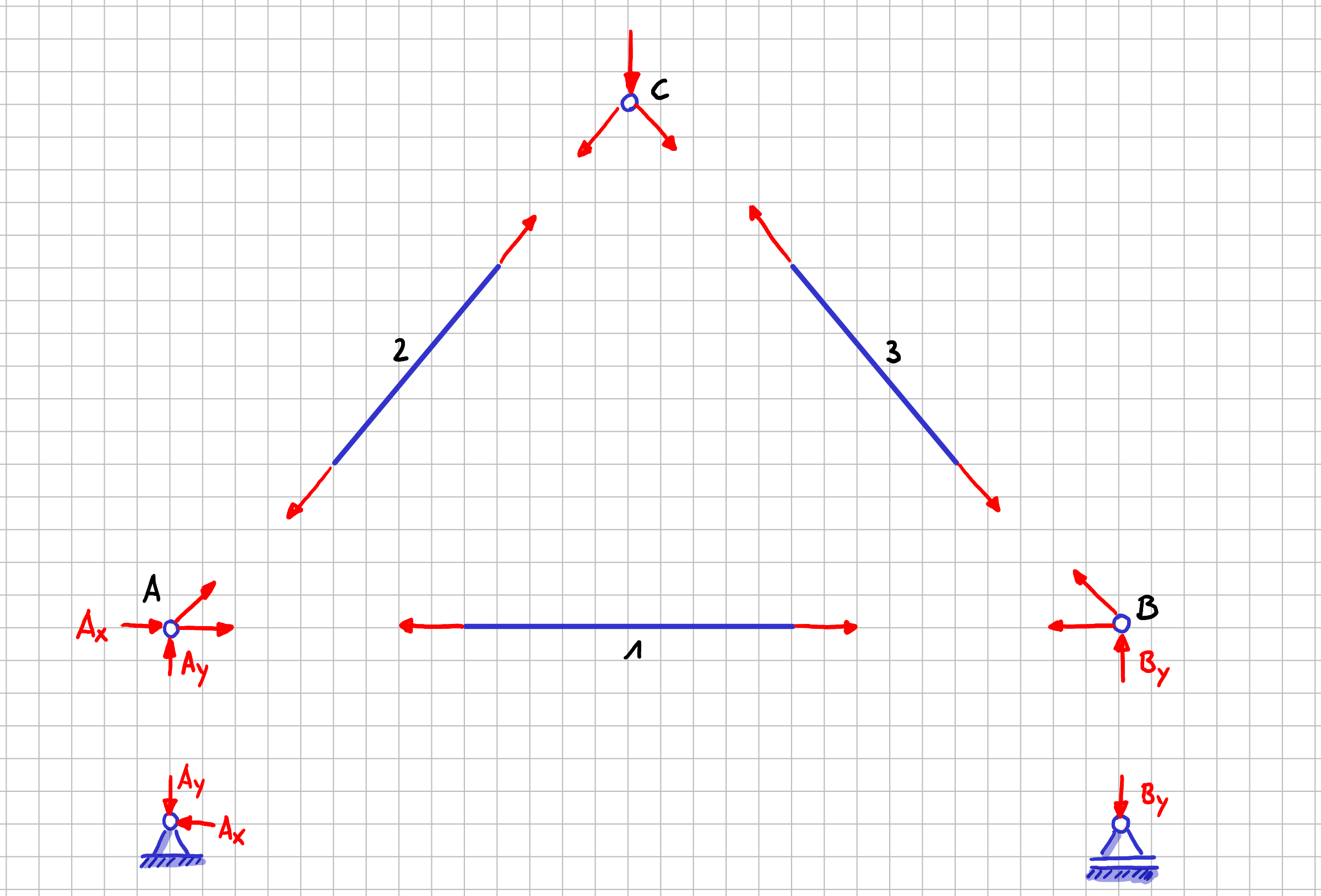
Vollständiges Freikörperbild für das Beispielfachwerk: Alle Stäbe und alle Knoten sind freigeschnitten

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_vollstaendiges_FKB.png

Eine gute Frage wäre jetzt, warum in den Freikörperbildern bei den Stäben nur Kräfte in Richtung der Stäbe eingezeichnet sind. Was ist mit Momenten und Kräften quer zur Stabrichtung? \( - \) Wir nehmen ja an, dass die Gelenke  reibungsfrei sind. Das erklärt schon mal, warum keine Momente auftauchen. Und die Kräfte quer zur Stabachse, was ist mit denen? Zeichne dir doch einfach mal das Freikörperbild eines Stabes hin, bei dem an beiden Enden nicht nur Kräfte IN Richtung des Stabes, sondern auch SENKRECHT dazu wirken.

Einen Stab mit Kraft senkrecht zur Stabachse kann es nicht geben

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Stab_mit_senkrechter_Kraft.png

Und jetzt stell in Gedanken oder durch Aufschreiben mal das Momentengleichgewicht um den Endpunkt \( A \) auf......tada....und schon siehst du, dass nur die besagte Kraft mal ihrem Hebelarm auftaucht. Und da der Hebelarm nachweislich nicht Null ist, heißt das, dass keine Kraft senkrecht zur Stabrichtung wirken kann.

Bis jetzt ist beim Thema "Fachwerk" also nicht wirklich viel neu. Du hast dir gerade selbst 'nur' mit Kenntnissen über das Freischneiden und das Aufstellen eines Momentengleichgewichts hergeleitet, was ein Stab ist:

Ein Element, was nur Kräfte in Stabrichtung übertragen kann. Das einzige, was du als neue Information brauchtest, waren die Annahmen, von denen du ja auch schon die zum Gelenk kanntest.

Bleibt noch die Frage, wie verhält es sich mit den Kräften in Richtung des Stabes? Du ahnst es vielleicht schon: Stell doch einfach mal ein Kräftegleichgewicht in Stabrichtung auf. Und schwups bekommst du heraus, dass die Kräfte an den Enden eines Stabes denselben Betrag haben und in entgegengesetzte Richtung zeigen.

Kräftegleichgewicht in Stabrichtung

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Kraeftegleichgewicht_in_Stabrichtung.png

Wie soll es denn auch anders sein? Es greift ja keine äußere Kraft entlang des Stabes an, und damit auch nicht in Stabrichtung.

Schon erstaunlich, wie weit du mit Freischneiden und Gleichgewichtsbedingungenaufstellen kommst, oder? 

In unserem Freikörperbild von vorhin können wir die Kräfte jetzt also auch noch benennen. Üblicherweise wird der Buchstabe \( S \) mit einem Index, der der Nummer des Stabes entspricht, verwendet. Und da wir anhand der Stäbe nicht mehr an Information bekommen, als dass die Stabkräfte an beiden Enden identisch sind, werden die Stäbe üblicher Weise im Freikörperbild gar nicht mit hingezeichnet.

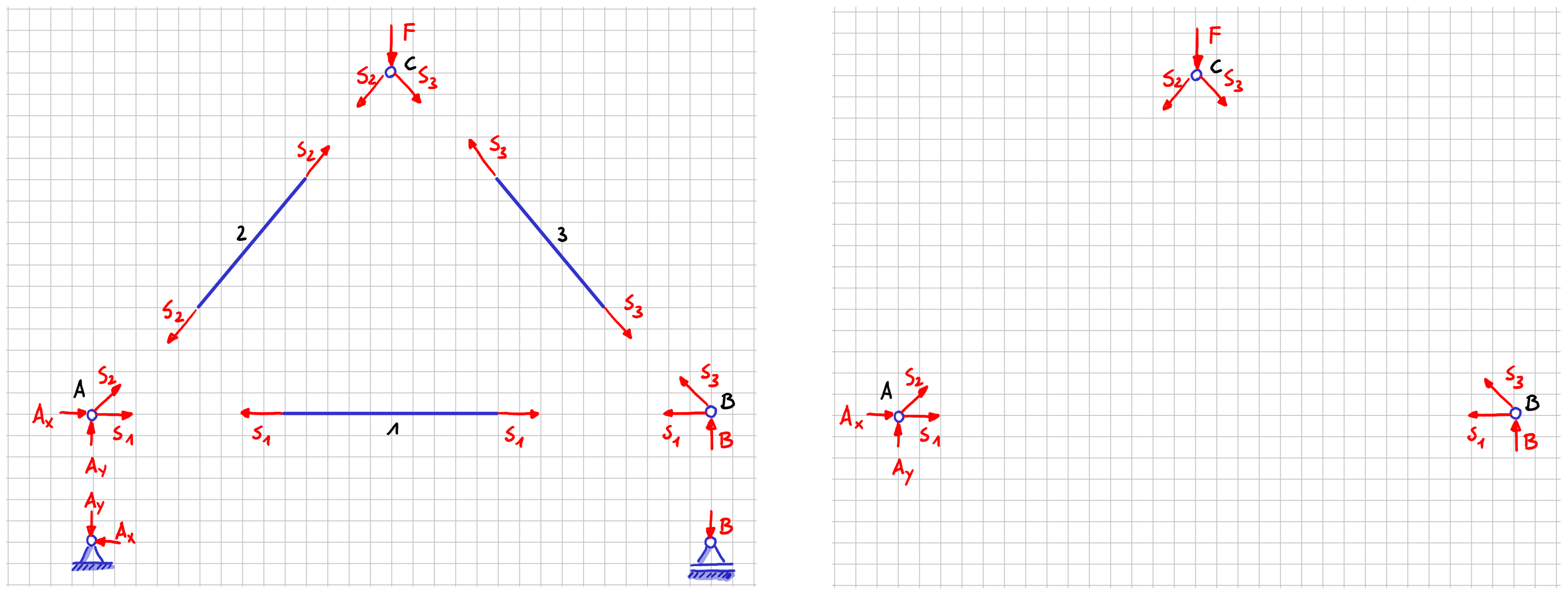
Gesamtfreikörperbild des Fachwerks: mit Stäben (links), ohne Stäbe (rechts)

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Beispiel_ideales_Fachwerk_mit_ohne_Staebe.png

Aber natürlich wollen wir die Stabkräfte auch wirklich ausrechnen. Darauf konzentrieren wir uns in den kommenden Abschnitten.
Wenn du magst, findest du vorher noch einen Exkurs zum Thema Schnittgrößen beim Stab. Wenn  du schauen möchtest, was du noch alles mit dem, was du eh schon kannst, herleiten kannst, schau den Exkurs gerne jetzt an. Ansonsten lohnt es sich den Exkurs auch erst dann anzuschauen, wenn du dich schon mit Schnittgrößen beschäftigt hast ... oder jetzt und später nochmal.

Exkurs zum Thema Gleichgewichtsbedingungen

Du hast jetzt schon soviel vom grundlegenden Handwerkszeug angewendet, da kannst du beim Stab auch einfach noch einen Schritt weitergehen. Du erinnerst vielleicht, dass ein wesentlicher Grundsatz in der Statik der folgende ist: Wenn ein Gesamtsystem im Gleichgewicht ist, ist auch jedes Teilsystem, das daraus herausgeschnitten wird, im Gleichgewicht, so lange geeignete Reaktionsgrößen an der Schnittstelle eingeführt werden. Bei der Betrachtung des ganzen Stabes weiter oben in dieser Lektion, den du aus dem Gesamtfachwerk herausgeschnitten hast, hast du genau dieses Prinzip ja gerade schon angewendet. Sonst hättest du ja gar keine Gleichgewichtsbedingungen aufstellen und die Schlussfolgerungen daraus ziehen können. 
Was passiert jetzt aber, wenn du einen Stab selbst noch einmal irgendwo entlang seine Länge auftrennst und anschließend wieder das Kräftegleichgewicht in Stabrichtung aufstellst, dieses Mal eben nur für eines der beiden Teilstücke?

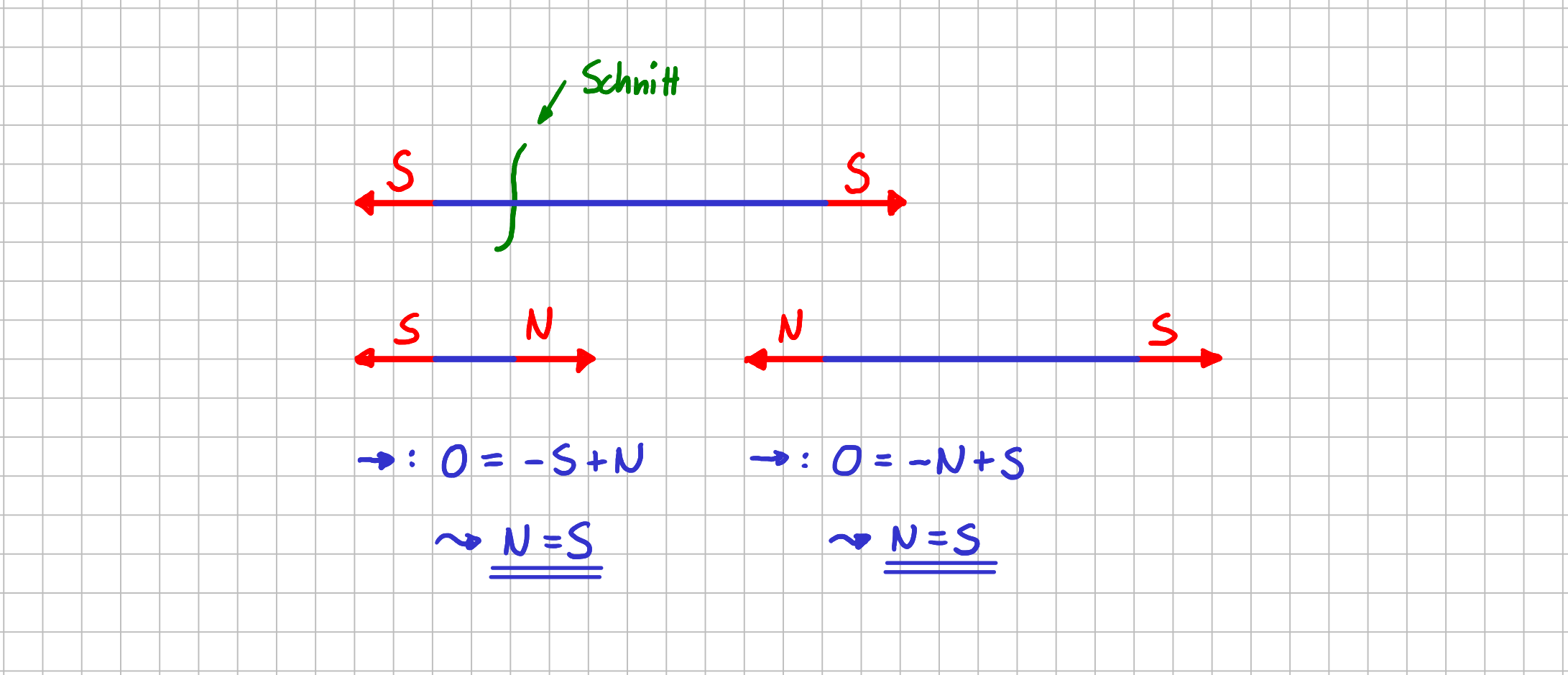
Stab und durchgeschnittener Stab mit innerer Kraft \( N \)

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2210/Stab_und_durchgeschnittener_Stab.png

Nachdem, was du jetzt schon über Stäbe weißt, kann an der Schnittstelle nur eine Kraft in Richtung des Stabes wirken. Wenn du diese Kraft \( N \) am linken Teilstück des Stabes vom Stab weg einzeichnest, zeigt sie wegen "Actio = Reactio" auch am rechten Teilstück vom Stab weg.

Wenn du für eines der beiden Teilstücke das Kräftegleichgewicht aufstellst, bekommst du heraus, dass die innere Kraft \( N \) vom Betrag her identisch der Kraft \( S \) am Stabende ist. Dabei ist es erwartungsgemäß egal, ob du das linke oder das rechte Teilstück betrachtest.

Damit hast du dir also auch noch selbst hergeleitet, was im Inneren eines Stabes los ist: dort wirkt an jeder Stelle entlang des Stabes dieselbe Kraft. Man nennt sie Normalkraft. Sie ist beim Stab nicht von der Lage der Schnittposition abhängig, sondern entlang des Stabes konstant und hat den Betrag der Stabkraft \( S \).