Fachwerk
Fachwerk
6. FAQs
FAQs
Zum Ende dieser Lektion findest du noch fünf Fragen, von denen ich ehrlich gesagt hoffe, dass du sie dir beim Bearbeiten der bisherigen Lektion schon gestellt hast. Wenn nicht, auch nicht schlimm. Dann hoffe ich, dass du einen Aha-Effekt hast, wenn du die folgenden Fragen und Antworten durcharbeitest.
1. Warum berechnen wir denn nicht auch beim Knotenpunktsverfahren als erstes die Lagerreaktionen?
Das ist eine sehr gute Frage. Ich habe es bei der Betrachtung des Fachwerks mit dem Knotenpunktsverfahren bewusst nicht getan, um zu zeigen, dass du direkt mit dem Knotenpunktsverfahren auch die Lagerreaktionen berechnen kannst. Natürlich heißt das nicht, dass du immer so vorgehen musst. Ganz im Gegenteil. Na klar kannst du auch bei einem Fachwerk als erstes die Lagerreaktionen berechnen, wenn du anschließend mit dem Knotenpunktsverfahren arbeiten willst, um Stabkräfte zu berechnen. Erlaubt ist alles, was dich deinem Ziel näher bringt. Logisch.
2. Kann ich nur entweder das Knotenpunktsverfahren oder den Ritterschnitt anwenden?
Du kannst natürlich auch beide Verfahren kombinieren. Du beachtest ja bei beiden Verfahren die grundlegenden Gesetze der Statik. Also: Sammle deine Erfahrungen und entscheide von Mal zu Mal neu, welches Verfahren du wann anwendest. Ich finde es immer beruhigend zu wissen, dass das Knotenpunktsverfahren für einfache Fachwerke immer funktioniert, um alle Lager- und Stabkräfte ausrechnen zu können. Richtig Spaß macht es aber erst, wenn ich einen Weg finde, der effizient und deshalb clever ist. Wenn du in einem ersten Schritt schon einige Kräfte per Ritterschnitt bestimmen kannst, ist das doch super. Dann wird es anschließend beim Knotenpunktsverfahren umso einfacher, weil du schon weniger Unbekannte übrig hast.
3. In Büchern oder anderen Informationsquellen gibt es immer auch einen Abschnitt über Nullstäbe. Warum gibt es den denn hier nicht?
Das ist gut beobaachtet, dass es diesen Abschnitt sonst eigentlich immer gibt. Aber mal ehrlich: brauchst du den wirklich? Ist es nicht viel cooler, dass du inzwischen weißt, wie du Nullstäbe finden kannst (ohne wirklich irgendwas auswendig zu lernen oder dir zusätzlich merken zu müssen)?
Schau dir das folgende Fachwerk an.
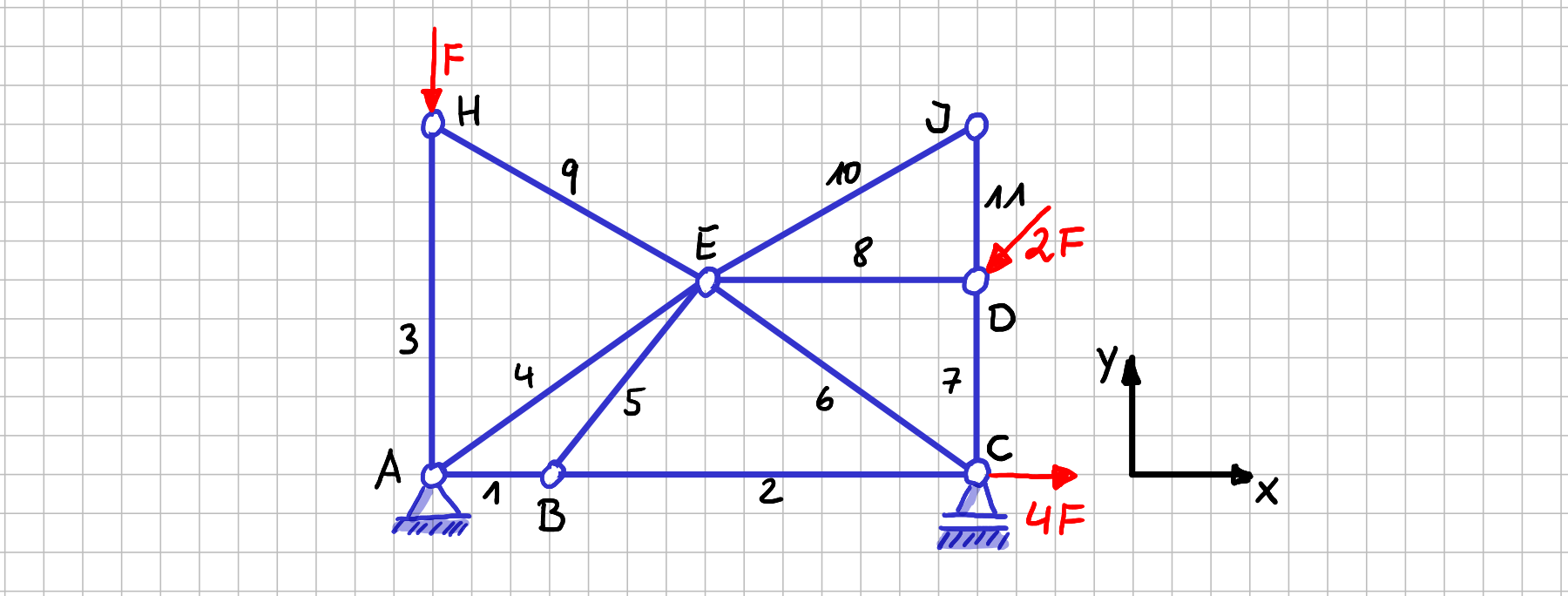
Beispielfachwerk zur Bestimmung von Nullstäben
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Beispielfachwerk_Nullstaebe.png
Wenn du offensichtliche Nullstäbe suchst, schaust du dir vorab Knoten einzeln an, schneidest sie also (gedanklich) aus dem System heraus. Bei welchen Knoten würdest du anfangen, nach offensichtlichen Nullstäben zu schauen? Bestimmt nicht bei Knoten \( E \), oder? Da ist ganz schön was los, da dort sechs Stäbe zusammentreffen. Auch nicht bei Knoten\( A \), da dort zwei Lagerkräfte und drei Stabkräfte als Unbekannte in den Gleichgewichtsbedingungen auftauchen. Für jeden Knoten kannst du ja nur die beiden Kräftegleichgewichte aufstellen. Also brauchst du Knoten, in deren Gleichgewichtsbedingungen maximal zwei Unbekannte auftreten. Du brauchst also Knoten, bei denen "wenig los" ist. Das ist z.B. bei Knoten \( J \)der Fall.
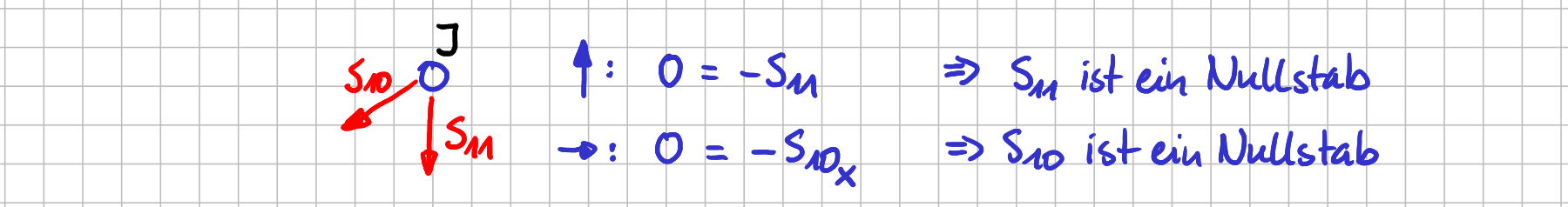
Freikörperbild von Knoten \( J \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_J.png
Die Stabkraft \( S_{11} \) greift an Knoten \( J \) als einzige Kraft in \( y \)-Richtung an. Stab 11 muss also ein Nullstab sein. Das sieht du auch sofort, wenn du für Knoten \( J \) das Kräftegleichgewicht in \( y \)-Richtung aufstellst. Und in \( x \)-Richtung ist \( S_{10} \) die einzige Kraft, die in diese Richtung eine Komponente hat. Also ist auch Stab 10 ein Nullstab. War doch ganz einfach, oder? Du hast nichts anderes getan, als freizuschneiden und hinzuschauen bzw. ein Kräftegleichgewicht aufzustellen. Und schon hast du Nullstäbe gefunden. Bei Knoten \( H \) ist auch wenig los.
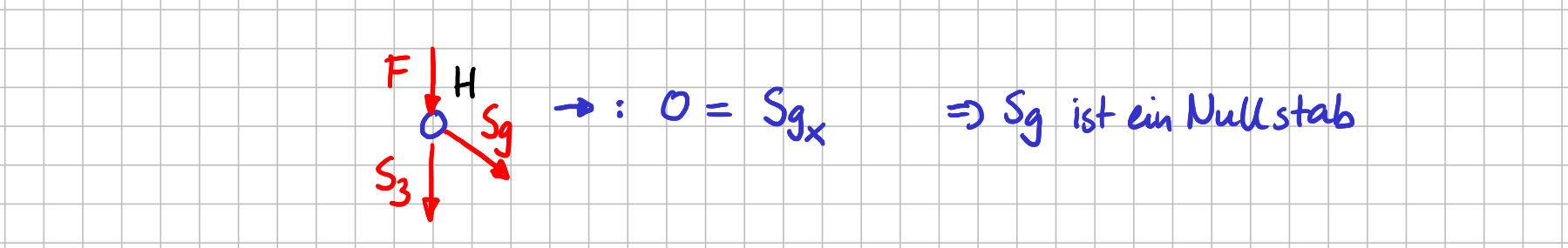
Freikörperbild von Knoten \( H \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_H.png
Hier siehst du im Kräftegleichgewicht in \( x \)-Richtung sofort, dass Stab 9 ein Nullstab ist, da die Kraft \( S_9 \) die einzige Kraft mit einer Komponente in \( x \)-Richtung ist. Und mit exakt denselben Argumenten findest du bei Knoten \( B \) heraus, dass Stab 5 ein Nullstab ist.
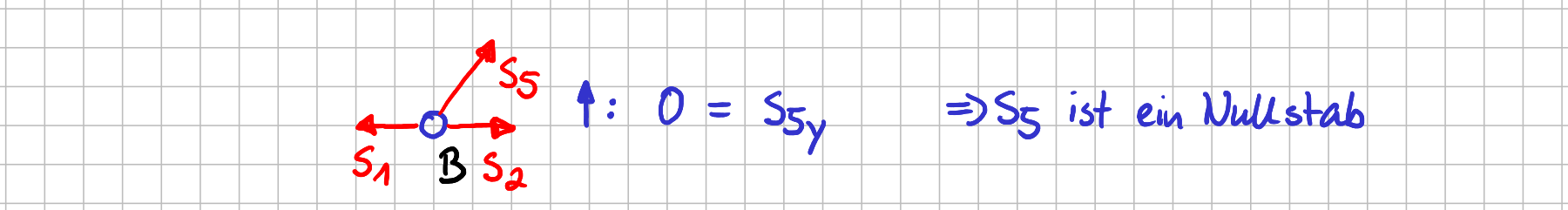
Freikörperbild von Knoten \( B \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_B.png
Hier ist es die Kraft \( S_5 \), die als einziges eine Komponente in \( y \)-Richtung hat.
Na gut, jetzt hast du doch noch einen Abschnitt über Nullstbe bekommen. Aber ich hoffe sehr, dass du siehst, dass es sich nicht lohnt, dir zu merken, was eine "unbelastete Ecke" ist oder in welchem Winkel irgendwelche Stäbe oder Kräfte zueinander stehen müssen, damit ein Stab ein Nullstab ist. Suche einfach nach Knoten, an den wenig los ist (= maximal zwei Unbekannte in den Gleichgewichtsbedingungen auftreten) und dann zeichnest du eben das Freikörperbild auf und schon siehst du, was los ist.
Am Ende dieser Seite findest du ganz viele Fachwerke, bei denen du üben kannst, die Nullstäbe zu finden.
4. Eine Kraft kann man in der Statik immer entlang Wirkungslinie verschieben, oder?
Das "immer" in diesem Satz ist nicht richtig. Schau dir das folgende Fachwerk an. Du siehst zwei Mal die gleiche Aufgabe. Der einzige Unterschied ist der Angriffspunkt der Kraft \( F \).
Eine Kraft kann entlang ihrer Wirkungslinie verschoben werden, solange die Wechselwirkung zwischen dem Gesamtsystem und der Umgebung betrachtet wird. Also immer, wenn du Lagerreaktionen berechnest, kannst du Kräfte entlang ihrer Wirkungslinie verschieben. An den Lagerreaktionen verändert sich dadurch nichts.
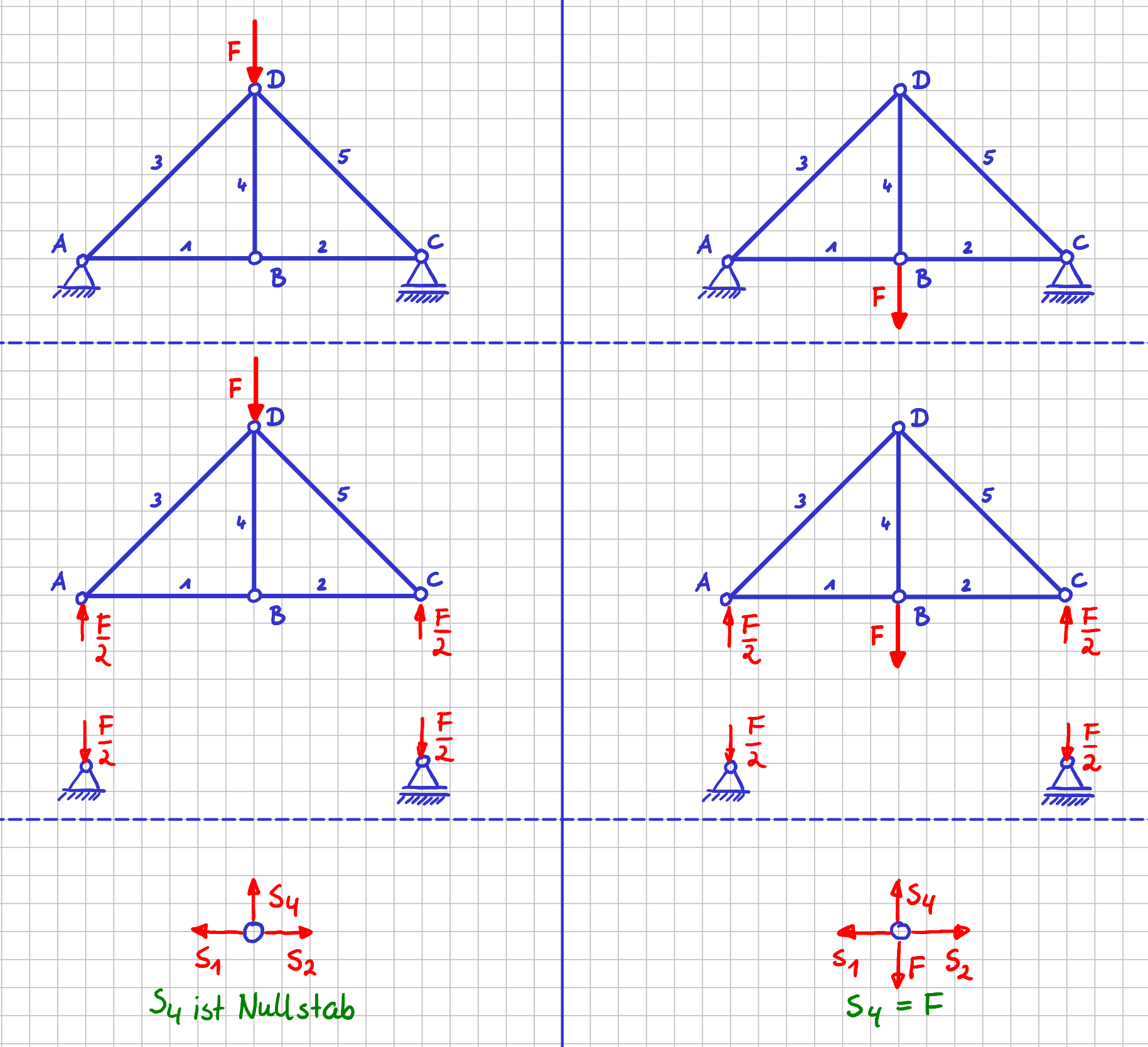
Veranschaulichung, wann eine Kraft entlang ihrer Wirkungslinie verschoben werden kann, und wann nicht
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Veranschaulichung_wann_Kraft_nicht_entlang_Wirkungslinie_verschieben.png
Wenn du aber ins Innere des Systems hineingehst, und das tust du ja, wenn du die Einzelkomponenten eines Systems betrachtest (hier beim Fachwerk sind das die Stäbe bzw. die Knoten), dann spielt es natürlich sehr wohl eine Rolle, wo die Kräfte angreifen. Im linken Fall ist Stab 4 ein Nullstab. Im rechten Fall ist der Betrag der Stabkraft gerade \( F \) .
5. Und was ist mit nichteinfachen Fachwerken?
Ein Fachwerk ist immer dann nichteinfach, wenn eine oder beide Bedingungen, die für einfache Fachwerke gelten müssen, verletzt sind. Heißt das automatisch, dass du dann gar nichts mehr berechnen kannst? Es kommt darauf an.
In der folgenden Abbildung siehst du ein nichteinfaches Fachwerk.
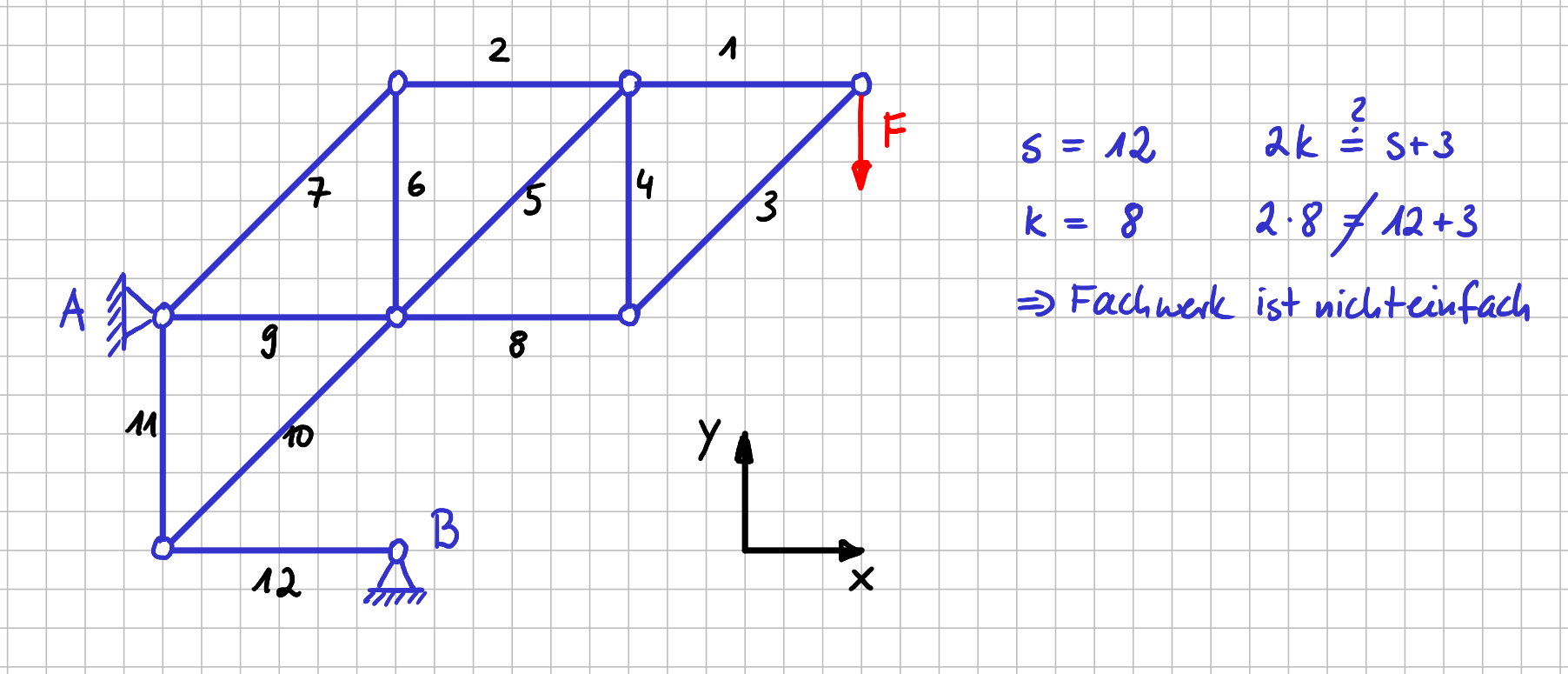
Beispiel für ein nichteinfaches Fachwerk
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Beispiel_nichteinfaches_Fachwerk.png
Und trotzdem kannst du in diesem Fall alle Lagerreaktionen und Stabkräfte berechnen. Warum? Weil am Festlager in Punkt \( B \) nur ein Stab in \( x \)-Richtung angreift, ist klar, dass die \( x \)-Komponoente der Reaktionskraft in Punkt \( B \), also \( B_y \) gleich Null sein muss. Außerdem ist \( B_x=S_{12} \).
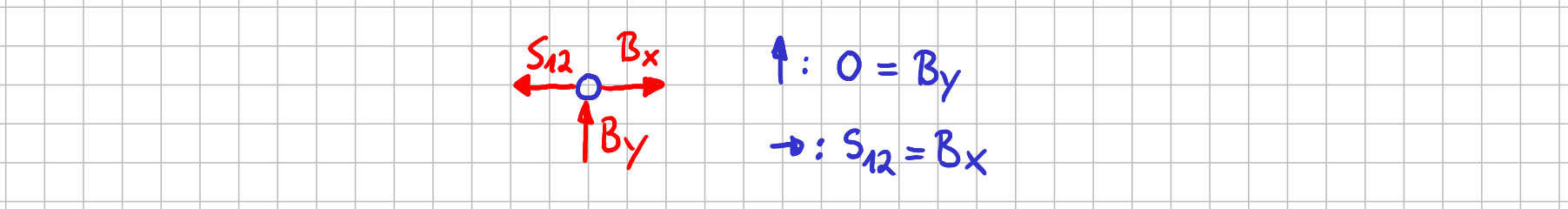
Freikörperbild Knoten \( B \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/FKB_Knoten_B_2.png
Mit diesen Informationen kannst du in einem ersten Schritt also das Festlager in Punkt \( B \) durch ein geeignet ausgerichtetes Loslager ersetzen. Und in einem zweiten Schritt kannst du Stab 12 entfernen und das Loslager nach links verschieben. Dann hast du es wieder mit einem einfachen Fachwerk zu tun.
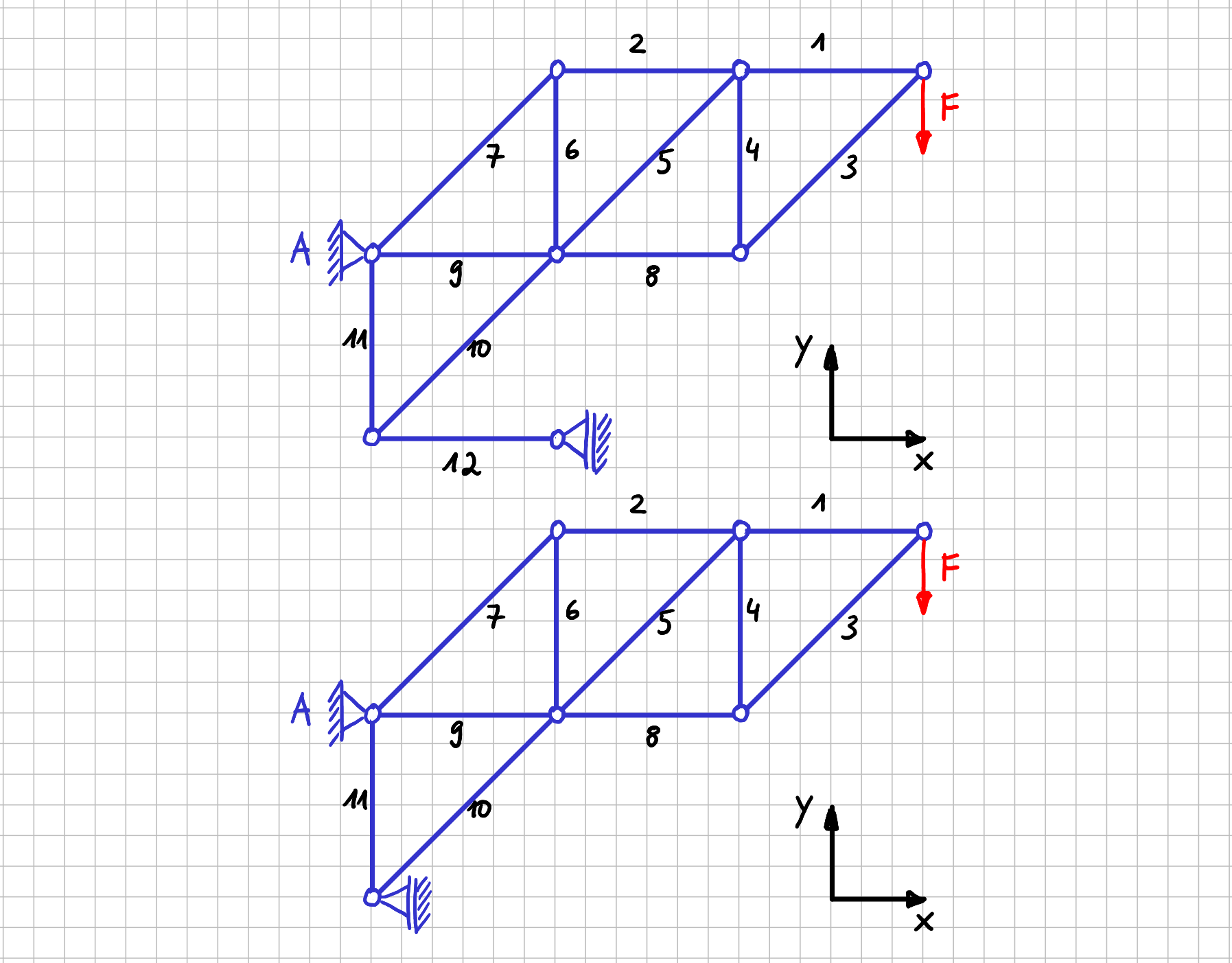
Umbau des Fachwerks unter Berücksichtigung der Erkenntnisse aus der Betrachtung von Knoten \( B \)
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13824/mod_book/chapter/2209/Umbau_des_Fachwerks.png
Es lohnt sich also, auch bei nichteinfachen Fachwerken genau hinzuschauen.
