Schwerpunkt
Schwerpunkt
6. Körper mit einfacher Geometrie
Körper mit einfacher Geometrie
Ein Hinweis vorab: ich werde im Folgenden ausschließlich mit Flächen arbeiten, um die Zusammenhänge darzustellen. Das hat rein zeichnerische Gründe. Alle Ergebnisse kannst du analog natürlich auch auf dreidimensionale Körper übertragen. Genaugenommen kannst du dir die Flächen im Folgenden als die Seiten eines dreidimensionalen Körpers vorstellen, der eine konstant Dicke in die Bildebene hinein hat. Flächen mit einfachen Geometrien sollen hier Flächen sein, die aus einfachen Einzelgeometrien wie Rechteck, Dreieck, Halbkreis etc. zusammengesetzt sind. Diese Teilflächen werden deshalb als 'einfach' bezeichnet, da für die Einzelflächen die Schwerpunktslagen bekannt sind. Daher lässt sich auch die Lage des Gesamtschwerpunktes sowohl zeichnerisch/rechnerisch als auch rein rechnerisch einfach bestimmen. Und genau das schauen wir uns jetzt an einem Beispiel, bei dem die Fläche aus zwei rechteckigen Einzelfächen besteht, an. Zwei jede der Rechteckflächen hat ja ihren Schwerpunkt \( S_1 \) bzw. \( S_2 \) in dem du dir ihre Masse konzentriert vorstellen kannst. Das hatten wir ja gerade schon. Der Schwerpunkt ist derjenige Punkt, für den das Momentengleichgewicht erfüllt ist, sich die Wirkungen der beiden einzelnen Gewichtskräfte also aufheben. Wenn die Gewichtskräfte mit \( G_1 \) und \( G_2 \) und die Hebelarme (senkrechter Abstand vom Einzelschwerpunkt zum Gesamtschwerpunkt) mit \( \ell_1 \) und \( \ell_2 \) bezeichnet werden, dann muss also gelten: \( G_1 \cdot \ell_1 = G_2 \cdot \ell_2 \).
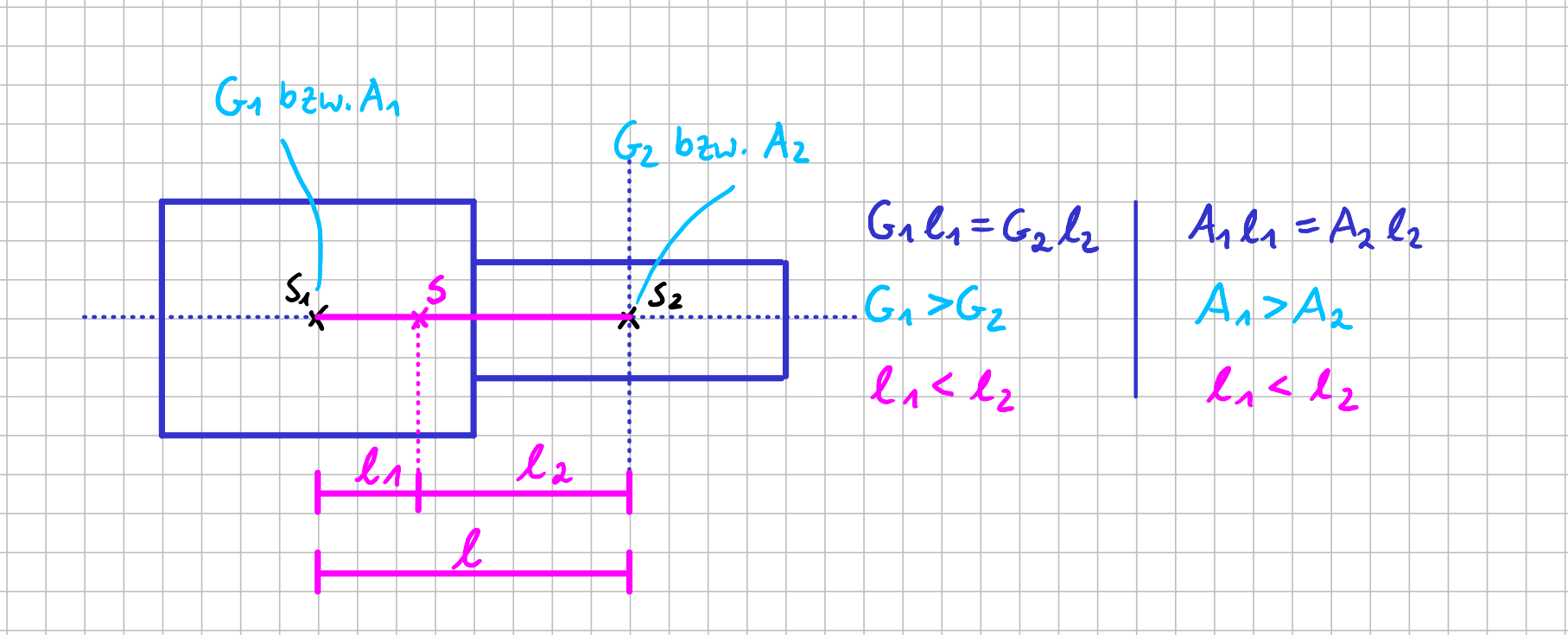
Bezeichnungen und Momentengleichgewicht
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Bezeichnungen_und_Momentengleichgewicht.png
Und wenn für den Abstand \( \ell \) der beiden Einzelschwerpunkte gilt \( \ell = \ell_1 + \ell_2 \) dann folgt daraus \( \ell_1=\ell- \ell_2 \) bzw. \( \ell_2 = \ell - \ell_1 \). Wenn du diese beiden Beziehungen in das Momentengleichgewicht einsetzt und umformst bekommst du folgende Beziehungen: $$ \dfrac{\ell_1}{\ell_2}=\dfrac{G_1}{G_2} \qquad \rightarrow \qquad \ell_1=\dfrac{G_2}{G_1+G_2}\ell, \qquad \ell_2=\dfrac{G_1}{G_1+G_2}\ell $$ Das Momentengleichgewicht sagt also nichts anderes aus, als dass die Verbindunglinie zwischen den Einzelschwerpunkten im umgekehrten Verhältnis der Gewichtskräfte \( G_i \) oder eben der Flächeninhalte \( A_i \) geteilt wird. Und um es ganz konrekt zu machen, findest du für verschiedenen Flächenverhältnisse Beispiele in der folgenden Abbildung.
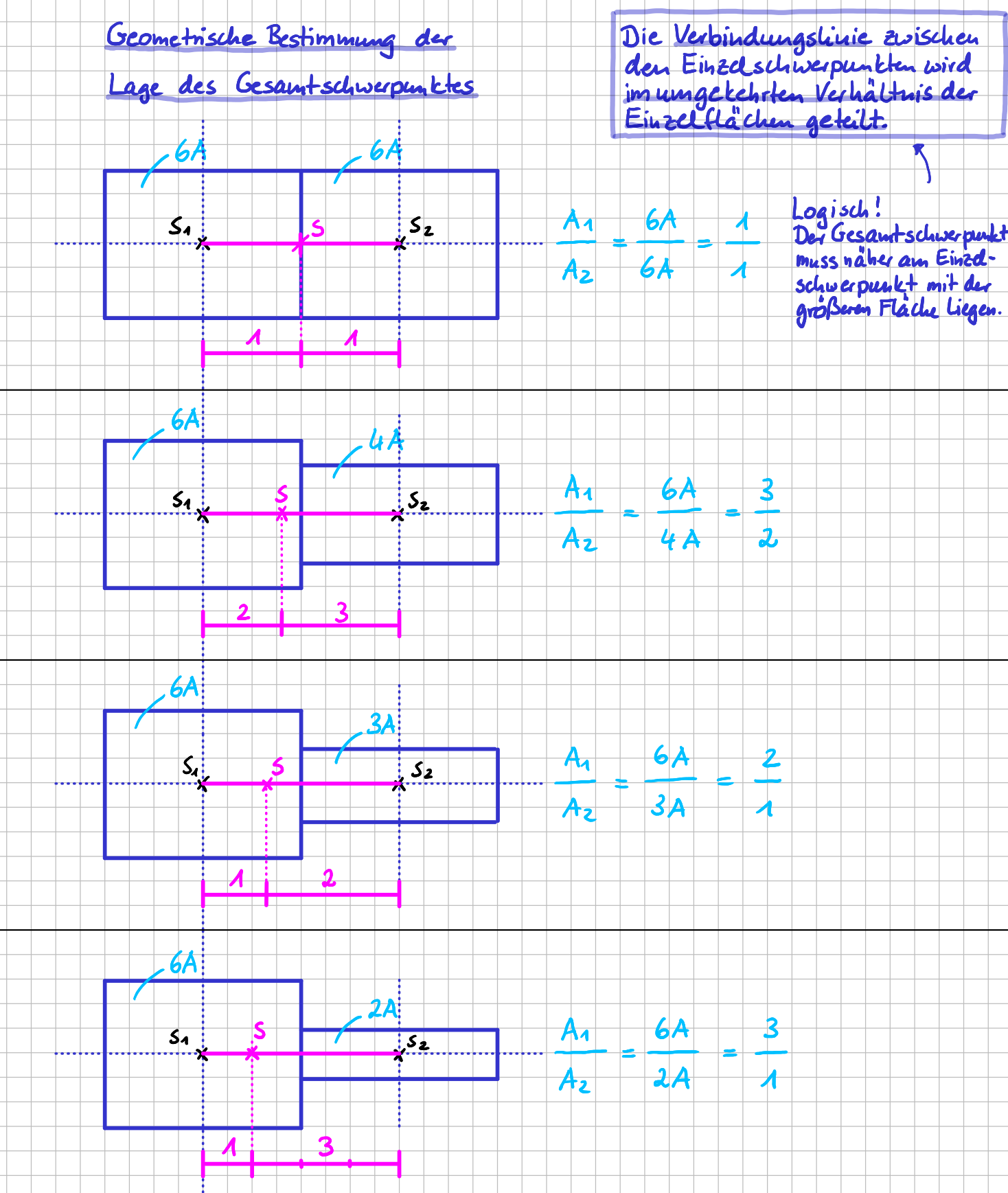
Beispiele für unterschiedliche Flächenverhältnisse: im umgekehrten Verhältnis wird die Verbindungslinie der Einzelschwerpunkte durch den Gesamtschwerpunkt geteilt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Beispiele_fuer_unterschiedliche_Flachenverhaeltnisse.png
Die Regel mit dem Teilen der Verbindungsstrecke gilt natürlich auch, wenn die Verbindungslinie nicht horizontal angeordnet ist. Dann lässt sich das Teilungsverhältnis auch auch die horizontale und vertikale Richtung übertragen, wie es in folgendem Beispiel zu sehen ist. Mathematisch gesehen sind ähnliche Dreiecke hier eine mögliche Basis für das Verständnis.
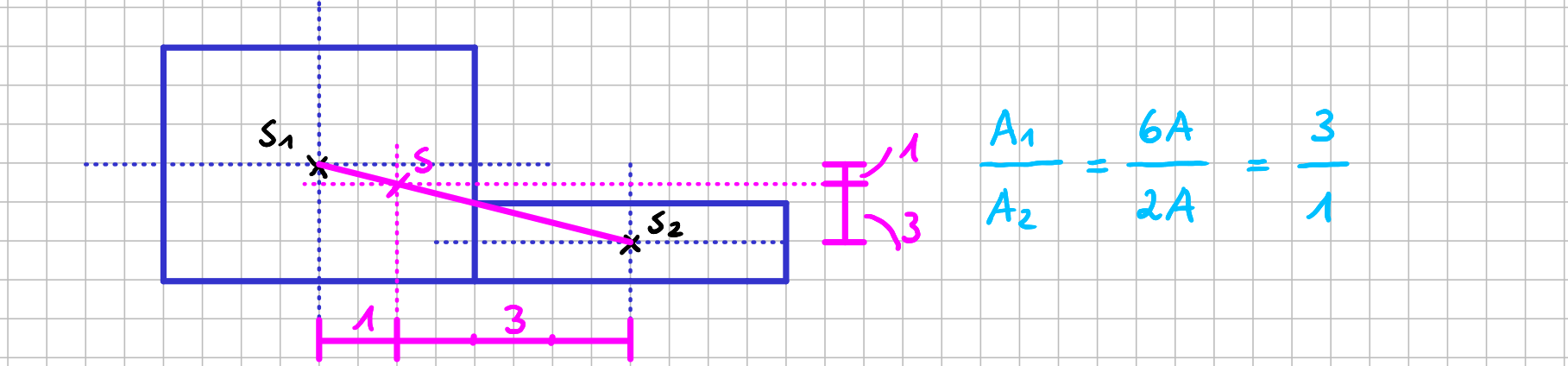
Teilungsverhältnisse bei nicht-horizontaler Lage der Verbindungslinie
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Teilungsverhaeltnisse_bei_nichthorizontaler_Lage.png
Jetzt bleibt noch die Frage, wie wir die bisherigen Erkenntnisse verallgemeinern und systematisch in eine Formel bringen können. Das Ergebnis sieht mit den Schwerpunktskoordinaten \( x_{Si}, y_{Si}, z_{Si} \) der Teilflächen \( A_i \) so aus:

Formeln für die Berechnung der Koordinaten des Gesamtschwerpunktes
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Formeln_fuer_die_Berechnung_der_Lage_des_Gesamtschwerpunktes.png
Wie gut, dass die mathematische Schreibweise so kurz und klar ist. Ansonsten müssten wir die Formel für die \( x \)-Koordinate des Gesamtschwerpunktes so schreiben ...

Formel für die Berechnung der x-Koordinate des Gesamtschwerpunktes in Worten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Formle_fuer_die_x_Koordinate_in_Worten.png
... was auch hilfreich ist, da nochmal in einer anderen Darstellung klar wird, was da physikalisch gesehen eigentlich überhalb und unterhalb des Bruchstrichs steht.
Mit Essen soll man ja nicht spielen. Aber beim Essen ein kleines Experiment auszuführen ist nach meiner Auffassung erlaubt. Mit einer Scheibe Toastbrot, die z.B. auf einem Brett balanciert wird, kannst du sehr gut überprüfen, wie sich die Schwerpunktslage verändert, wenn noch ein Element hinzukommt (ein Stück Käse) oder ein Element weggenommen wir (einmal beherzt zubeißen). Auf dem ersten Foto siehts du den Versuchsaufbau. Auf dem zweiten Bild ist in rot markiert, wo das Brett langläuft, wenn nur das Toastbrot ausbalanciert wird. Auf dem dritten Bild siehst du anhand der blauen Linie, dass sich der Gesamtschwerpunkt nach rechts verschiebt, da ich den Käse an die rechte Kante der Toastscheibe gelegt habe. Der Gesamtschwerpunkt verschiebt sich auch nach rechts, wenn ich links durch Abbeißen Masse wegnehme.

Frühstücksversuch zur Schwerpunktsbestimmung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Fruehstuecksversuch_zur_Schwerpunktsbestimmung.png
Wie du siehst, war die Masse des Käsestücks größer, als die Masse des Toasteils, den ich abgebissen habe. Nach dem Abbeißen ist die blaue Linie um eine geringere Distanz nach rechts verschoben als nach dem Auflegen des Käsestücks. Lass uns den Toastbroatversuch auch gleich mal rechnerisch nachvollziehen. Wie Dir sicherlich aufgefallen ist, haben wir bisher noch gar kein Koordinatensystem, verwendet, sondern rein geometrisch argumentiert. Und wie immer gilt: Der Physik ist es egal, wie wir unser Koordinatensystem wählen. Wir können also nichts falsch machen, uns allerdings bemühen es möglichst clever tun. Und da ich bei dem Versuch darauf geachtet habe, dass alle Veränderungen symmetrisch sind, können wir eine Koordinatenachse auch auf die Symmetrieachse legen. Damit wissen wir schon mal sicher, dass die \( y \)-Koordinate des Gesamtschwerpunktes Null ist, also \( y_S=0 \) gilt. Die \( x_S \)-Koordinate können wir mit der besagten Formel leicht ausrechen.
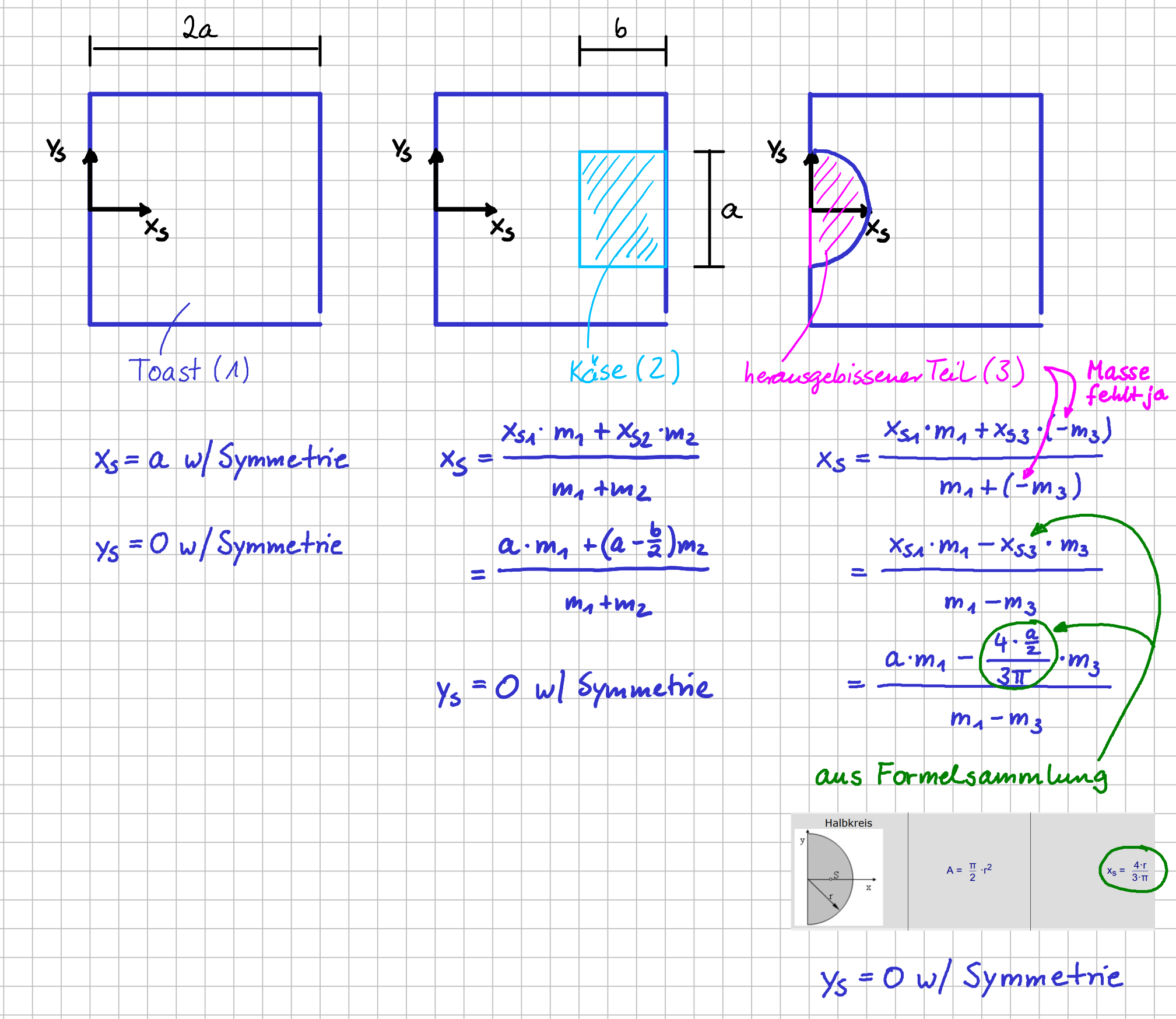
Frühstücksversuch in Formeln
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Fruehstuecksversuch_in_Formeln.png
Du kannst dir sicherlich vorstellen, dass es schnell unübersichtlich wird, wenn du mehr als zwei Massen oder Flächen zu berücksichtigen hast und du die Werte gleich in die der Bruchschreibweise mit Summen in Zähler und Nenner reinschreibst. Um die Übersicht zu behalten, ist es hilfreich, alle benötigten Werte und deren Produkte erstmal in einer Tabelle zusammenzustellen, dann über die Spalten zu summieren und nur die Ergebnisse aus den Spalten in den jeweiligen Bruch zu schreiben. Wie das geht, siehst du im Beispiel in der folgenden Abbildung. Ich habe bewusst verschiedene Rechenwege gewählt, damit du siehst, dass es sich lohnt, dir vorab Gedanken zu machen und alles Wissen, wie z.B. das über Symmetrien aber auch über mögliche Zerlegungen der Gesamtfläche zu nutzen.
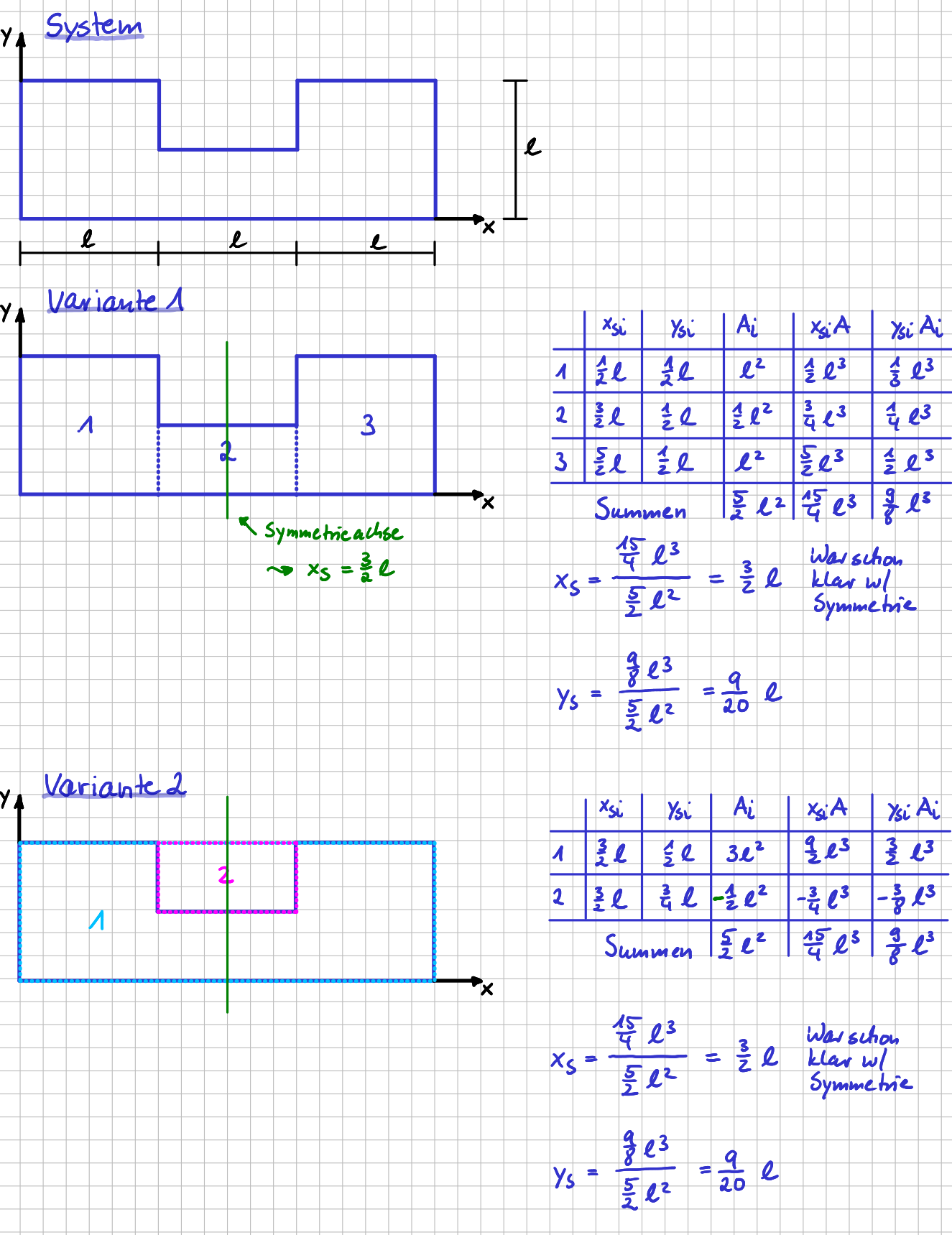
Übersicht behalten mit tabellarischer Erfassung der Werte
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Uebersicht_behalten_mit_Tabelle.png
