Schwerpunkt
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Schwerpunkt |
| Gedruckt von: | Gast |
| Datum: | Freitag, 23. Oktober 2026, 02:06 |
1. Einstieg Schwerpunkt
Einstieg Schwerpunkt
Wilmas Mechanikwelt
Schwerpunkt ganz praktisch
Ich habe heute mal ganz praktische Versuche zum Thema Schwerpunkt gemacht.
Hat ne Weile gedauert, bis ich die Schwerpunktslage bei dem Stock gefunden hatte. Ist aber auch ganz schön schwierig. Die Dichte vom Holz ist schon nicht konstant und dann hat sich der Stock auch noch unterschiedlich mit Wasser vollgesogen.
Schwerpunktsexperiment mit einem inhomogenen Körper.
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2205/Wilma_Schwerpunkt.png
2. Eigene Erfahrungen mit Schwerpunkten
Eigene Erfahrungen mit Schwerpunkten
Beim Schwerpunkt weiß auf eine gewisse Art und Weise wirklich jeder intuitiv, was dieser Punkt ist und wo er bei einem Objekt liegt. Wir alle haben als Kinder vermutlich schon versucht, z.B. einen Stock oder einen Esslöffel auf dem Finger auszubalancieren oder ihn in Waage zu halten. Oder wir haben selbst auf einem Geländer balanciert.
Korrektes Positionieren des Schwerpunktes ausdrücklich erwünscht
Weitere Informationen
Macrovector; mit Ergänzungen von Johanna Peters | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2206/Korrektes_Positionieren_ausdruecklich_erwuenscht.png
Der Schwerpunkt eines Körpers ist also ein besonderer Punkt. Wenn du einen Körper in diesem Punkt "aufspießen" könntest, so dass er sich frei drehen kann, würde er in jeder beliebigen Lage seine Position halten. Mechanisch gesprochen bedeutet das: Das Momentengleichgewicht bezüglich dieses Punktes ist um alle Achsen erfüllt. In der folgenden Abbildung siehst du das am Beispiel eines Akkuschraubers.
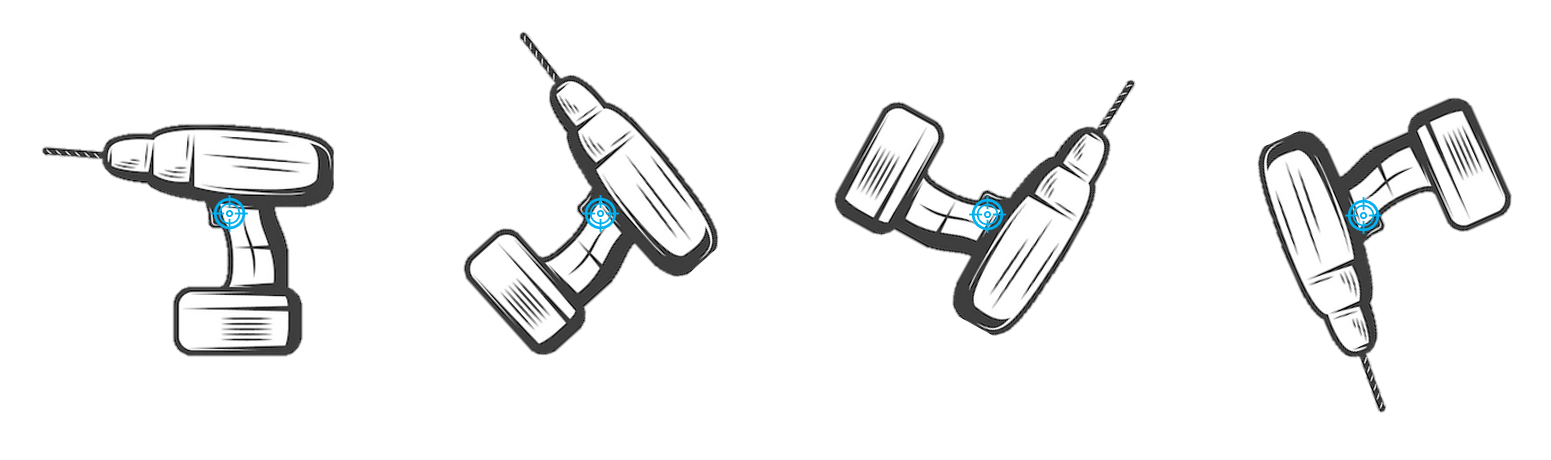
Im Schwerpunkt "aufgespießt" hält ein Körper jede Position auch nach Verdrehen ein
Weitere Informationen
Macrovector; mit Ergänzungen von Johanna Peters | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2206/Im_Schwerpunkt_aufgespiesst.png
Der Schwerpunkt ist also der Punkt, in dem du dir die aus den einzelnen Masseelementen \( \mathrm{d}m \) resultierenden Gewichtskräfte \( \mathrm{d}G \) eines Körpers als Einzelkraft \( G \) konzentriert vorstellen kannst.
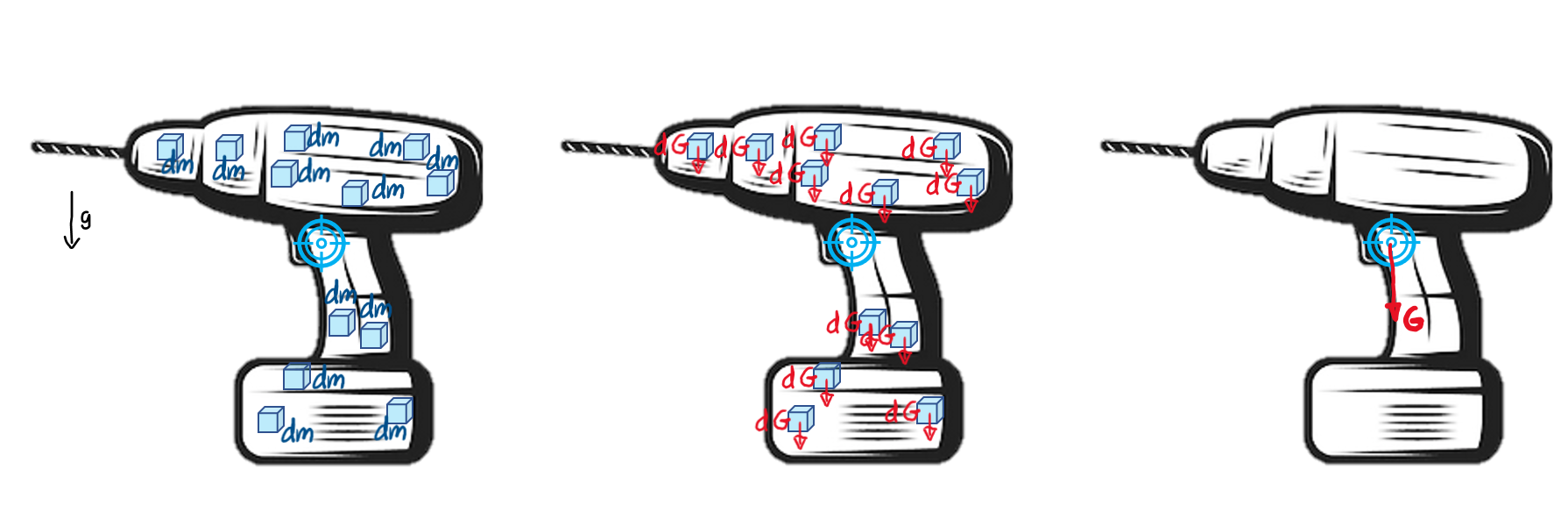
Schwerpunkt als Punkt in dem die konzentrierte Einzelkraft 'Gewichtskraft' angreift
Weitere Informationen
Macrovetor; mit Ergänzungen von Johanna Peters | TU Hamburg
Freepik License
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2206/Schwerpunkt_konzentrierte_Einzelkraft.png
3. Beispiele für Anwendungen in der Praxis
Beispiele für Anwendungen in der Praxis
In technischen Anwendungen ist es an verschiedenen Stellen wichtig, die Lage des Schwerpunktes zu kennen. Werden schwere Komponenten, wie z.B. die Gondel eines Windrades, mit einem Kran in Position gebracht, muss die Schwerpunktslage während des Hebevorgangs vorab geplant werden, um das Gegengewicht beim Kran entsprechend auswählen und seine Position justieren zu können.
Zwei verschiedene Krane mit unterschiedlichen Konzepten für das Gegengewicht bei der Montage der Gondel einer Windkraftanlage
Weitere Informationen
Willi Wilhelm, Badenweiler
coming soon
Bildquelle
Bei jedem Transport von Gütern mit einer relevanten Masse sollte die Schwerpunktslage überprüft werden. Anderenfalls kann es aufgrund einer ungleichmäßigen Belastung von Lagern zu übermäßigem Verschleiß kommen. Oder die Kippstabililtät des Transportmittels ist nicht gegeben und Fahrzeug samt Ladung kippen um.
Bei veränderlichen Massen sollte besonders auf die Schwerpunktslage geachtet werden, wie in dem folgenden Video deutlich wird.
Wissen über die veränderliche Lage des Schwerpunktes nicht berücksichtigt
Hast du schon mal darüber nachgedacht, was es eigentlich braucht, um eine Brücke zu bauen? Ich meine eine große Brücke ... eine Brücke, über die dann auch Fahrzeuge fahren können. Vermutlich denkst du, dass man dafür irgendeine Form von Kran braucht, oder? Könntest du dir vorstellen, dass es auch ohne Kran geht und nur mit dem Wissen über die Lage des Schwerpunktes? Lass dich überraschen und schau dir das Video an.
Wissen über die Lage vom Schwerpunkt clever angewendet: Brücken bauen
Wenn du dich noch ein bisschen weiter mit dem Gedanken "Lage des Schwerpunktes beim Überqueren einer Schlucht" beschäftigen möchtest, kann ich dir das nächste Video noch sehr empfehlen. Hier wird auf sehr kreative Weise eine Schlucht überquert, deren Breite nach und nach vergrößert wird. Immer dann, wenn eine Methode nicht mehr funktioniert, gibt es einen neuen kreativen Ansatz. Aber schaue es dir einfach selbst an.
Wissen über die Lage vom Schwerpunkt clever angewendet: immer breiter werdende Schlucht total elegant überwinden
Ich weiß leider nicht, wer der Urheber des Videos ist. Wenn du es selber bist oder ihn kennst, schicke die Infos gerne an mich (mechanikhautnah[at]tuhh.de), damit ich die Quelle korrekt angeben kann.
4. Experimentelle Bestimmung der Schwerpunktslage eines Körpers
Experimentelle Bestimmung der Schwerpunktslage eines Körpers
Ein Körper wird sich immer so hinhängen (müssen), dass der Gesamtschwerpunkt unter dem Aufhängungspunkt ist. Nur dann ist das Momentengleichgewicht erfüllt da nur in diesem Fall die Wirkungslinie der Gewichtskraft durch den Aufhängungspunkt geht und kein Moment bezüglich dieses Punktes erzeugt. Dies lässt sich am Beispiel eines Gehstocks oder Schirms besonders gut sehen:
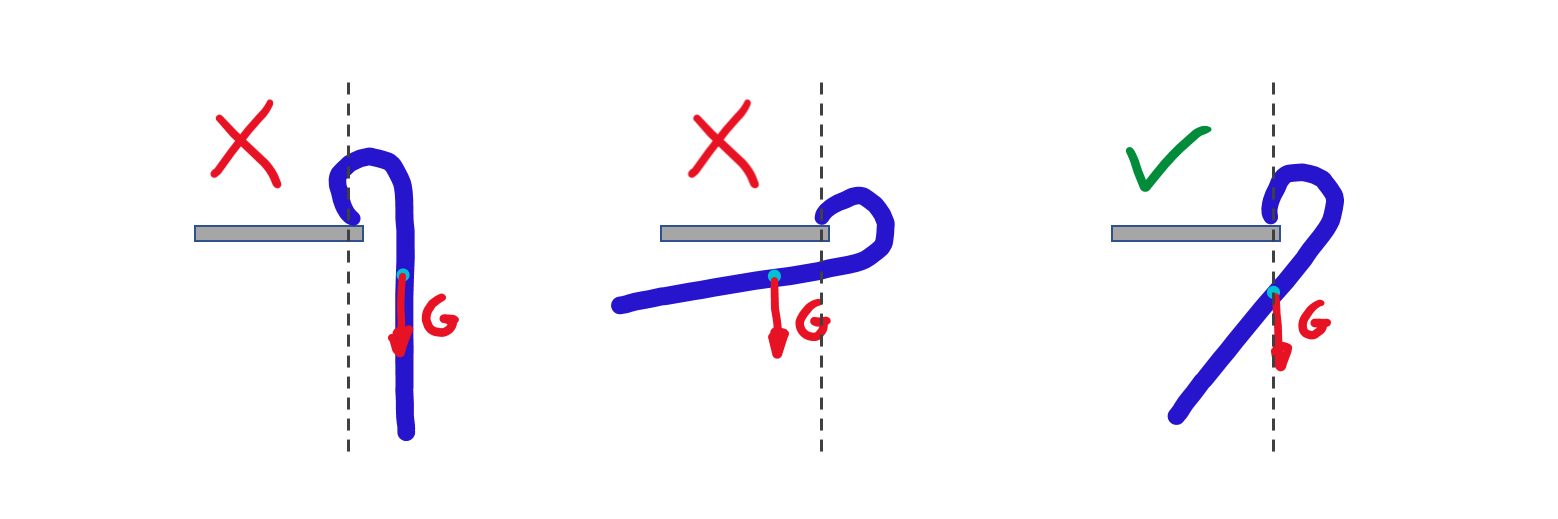
Auspendeln eines Gehstocks
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2207/Auspendeln_eines_Gehstocks.png
Da das Objekt hin- und herpendelt, bis der Schwerpunkt unterhalb des Aufhängepunktes zur Ruhe gekommen ist, wird ein solcher Versuch auch Pendelversuch und das Vorgehen Auspendeln genannt. Damit hast du gleich schon eine Möglichkeit zur Verfügung, für beliebig komplexe Geometrien den Schwerpunkt im Experiment zu bestimmen. Du musst einen Körper nur mehrmals an unterschiedlichen Punkten so aufhängen, dass er sich frei auspendeln kann. Die Linie, die durch den Aufhängepunkt in Richtung des Erdbeschleunigungsvektors zeigt, markierst du dir einem Foto von deinem Körper. Wenn du den Körper an zwei unterschiedlichen Punkten aufhängst, das Ganze also zwei Mal gemacht hast, hast du zwei Linien, die sich schneiden. Und dieser Schnittpunkt ist dann genau der Schwerpunkt. Da es in jedem Experiment Ungenauigkeiten gibt, kannst du den Versuch eventuell mit ein oder zwei weiteren Aufhängepunkten machen. Dann kannst du einen gemittelten Schnittpunkt aller erhaltenen Linien bestimmen. Je nach Körper und Verteilung der Masse ist der Schwerpunkt dabei nicht immer ein Punkt, der auch im Körper liegt. Der Schwerpunkt kann also auch außerhalb des Körpers, so zu sagen in der Luft, liegen.
Merle hat z.B. mit einer Brille über das Auspendeln den Schwerpunkt bestimmt und festgestellt, dass der Schwerpunkt 'in der Luft' ist.
Experimentelle Bestimmung der Schwerpunktslage einer Brille
Weitere Informationen
Experimentelle Bestimmung der Schwerpunktslage eines Schere
Weitere Informationen
Experimentelle Bestimmung der Schwerpunktslage eines Klebezettelblocks
Weitere Informationen
5. Symmetrieachsen als Wegweiser
Symmetrieachsen als Wegweiser
Viele Körper sind ja gar nicht so komplex: oft kann von einer in guter Näherung gleichmäßigen Masseverteilung ausgegangen werden. Und es gibt Symmetrien in der Geometrie. Da ich gerade im Auto sitze, während ich diese Lektion vorbereite: Ein Autolenkrad hat z.B. eine Symmetrieachse. Damit ist sofort klar, auf welcher Achse der Schwerpunkt liegen muss: Genau auf dieser Symmetrieachse.
Autolenkrad mit angedeuteter Symmetrieachse: Irgendwo hier muss der Schwerpunkt liegen
Weitere Informationen
ViDIstudio, mit Ergänzungen von Johanna Peters | TU Hamburg
Freepik
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2208/Autolenkrad_mit_Syymetrieachse.png
https://de.freepik.com/fotos-kostenlos/eine-junge-europaeerin-mit-gesunder-sauberer-haut-legte-ihre-haende-mit-roter-manikuere-auf-ihre-naegel-auf-das-lenkrad-des-autos-mit-schwarzem-interieur-reise-und-fahrkonzept_16557421.htm
Und wenn es mehrere Symmetrieachsen gibt, dann ist der Schnittpunkt dieser Achsen der Schwerpunkt.
Hantel als Beispiel für einen Körper mit mehreren Symmetrieachsen: Der Schnittpunkt der Symmetrieachsen ist der Schwerpunkt
Weitere Informationen
Macrovector, mit Ergänzungen von Johanna Peters | TU Hamburg
Freepik
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2208/Hantel_mit_Symmetrieachse.png
https://de.freepik.com/vektoren-kostenlos/kurzhanteln-hanteln-und-fitness_3949273.htm
6. Körper mit einfacher Geometrie
Körper mit einfacher Geometrie
Ein Hinweis vorab: ich werde im Folgenden ausschließlich mit Flächen arbeiten, um die Zusammenhänge darzustellen. Das hat rein zeichnerische Gründe. Alle Ergebnisse kannst du analog natürlich auch auf dreidimensionale Körper übertragen. Genaugenommen kannst du dir die Flächen im Folgenden als die Seiten eines dreidimensionalen Körpers vorstellen, der eine konstant Dicke in die Bildebene hinein hat.
Flächen mit einfachen Geometrien sollen hier Flächen sein, die aus einfachen Einzelgeometrien wie Rechteck, Dreieck, Halbkreis etc. zusammengesetzt sind. Diese Teilflächen werden deshalb als 'einfach' bezeichnet, da für die Einzelflächen die Schwerpunktslagen bekannt sind. Daher lässt sich auch die Lage des Gesamtschwerpunktes sowohl zeichnerisch/rechnerisch als auch rein rechnerisch einfach bestimmen. Und genau das schauen wir uns jetzt an einem Beispiel, bei dem die Fläche aus zwei rechteckigen Einzelfächen besteht, an. Zwei jede der Rechteckflächen hat ja ihren Schwerpunkt \( S_1 \) bzw. \( S_2 \) in dem du dir ihre Masse konzentriert vorstellen kannst. Das hatten wir ja gerade schon. Der Schwerpunkt \(S\) ist derjenige Punkt, für den das Momentengleichgewicht erfüllt ist, sich die Wirkungen der beiden einzelnen Gewichtskräfte also aufheben. Wenn die Gewichtskräfte mit \( G_1 \) und \( G_2 \) und die Hebelarme (senkrechter Abstand vom Einzelschwerpunkt zum Gesamtschwerpunkt) mit \( \ell_1 \) und \( \ell_2 \) bezeichnet werden, dann muss also gelten: \( G_1 \cdot \ell_1 = G_2 \cdot \ell_2 \).
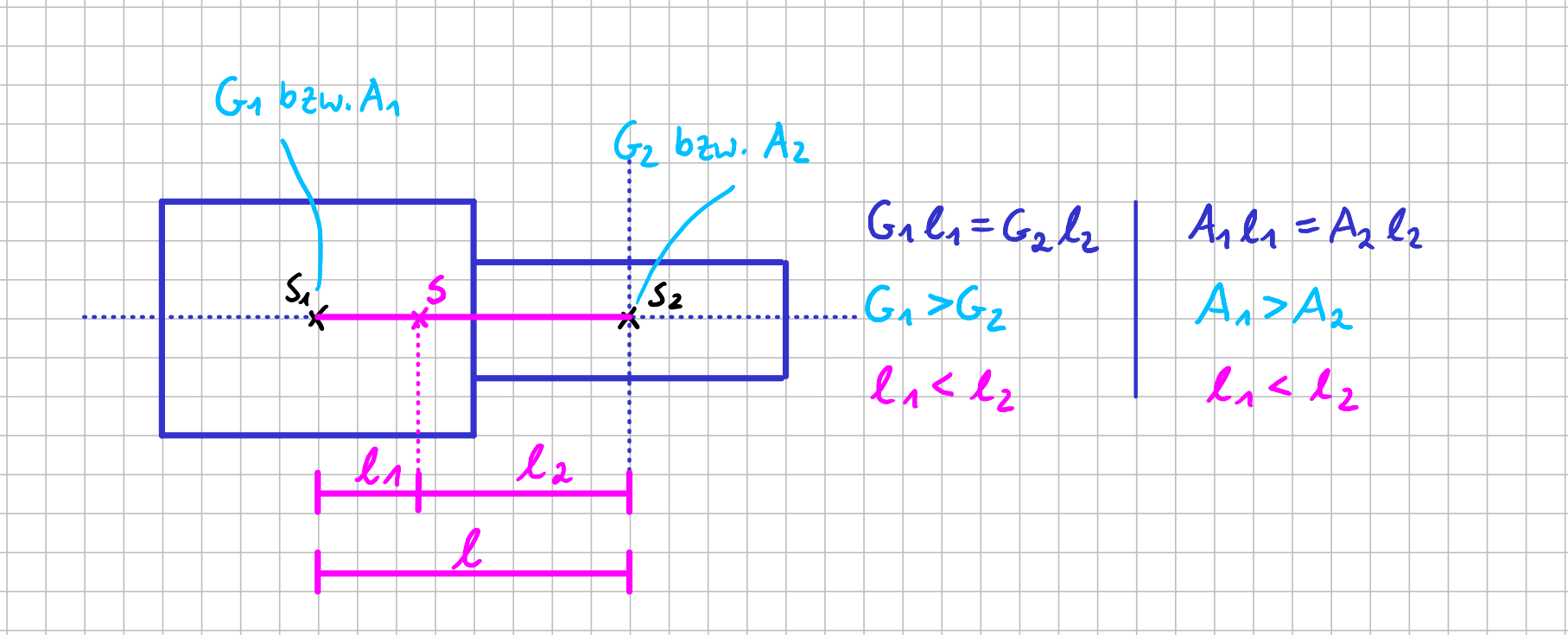
Bezeichnungen und Momentengleichgewicht
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Bezeichnungen_und_Momentengleichgewicht.png
Und wenn für den Abstand \( \ell \) der beiden Einzelschwerpunkte gilt \( \ell = \ell_1 + \ell_2 \) dann folgt daraus \( \ell_1=\ell- \ell_2 \) bzw. \( \ell_2 = \ell - \ell_1 \). Wenn du diese beiden Beziehungen in das Momentengleichgewicht einsetzt und umformst bekommst du folgende Beziehungen: $$ \dfrac{\ell_1}{\ell_2}=\dfrac{G_1}{G_2} \qquad \rightarrow \qquad \ell_1=\dfrac{G_2}{G_1+G_2}\ell, \qquad \ell_2=\dfrac{G_1}{G_1+G_2}\ell $$ Das Momentengleichgewicht sagt also nichts anderes aus, als dass die Verbindunglinie zwischen den Einzelschwerpunkten im umgekehrten Verhältnis der Gewichtskräfte \( G_i \) oder eben der Flächeninhalte \( A_i \) geteilt wird. Und um es ganz konrekt zu machen, findest du für verschiedenen Flächenverhältnisse Beispiele in der folgenden Abbildung.
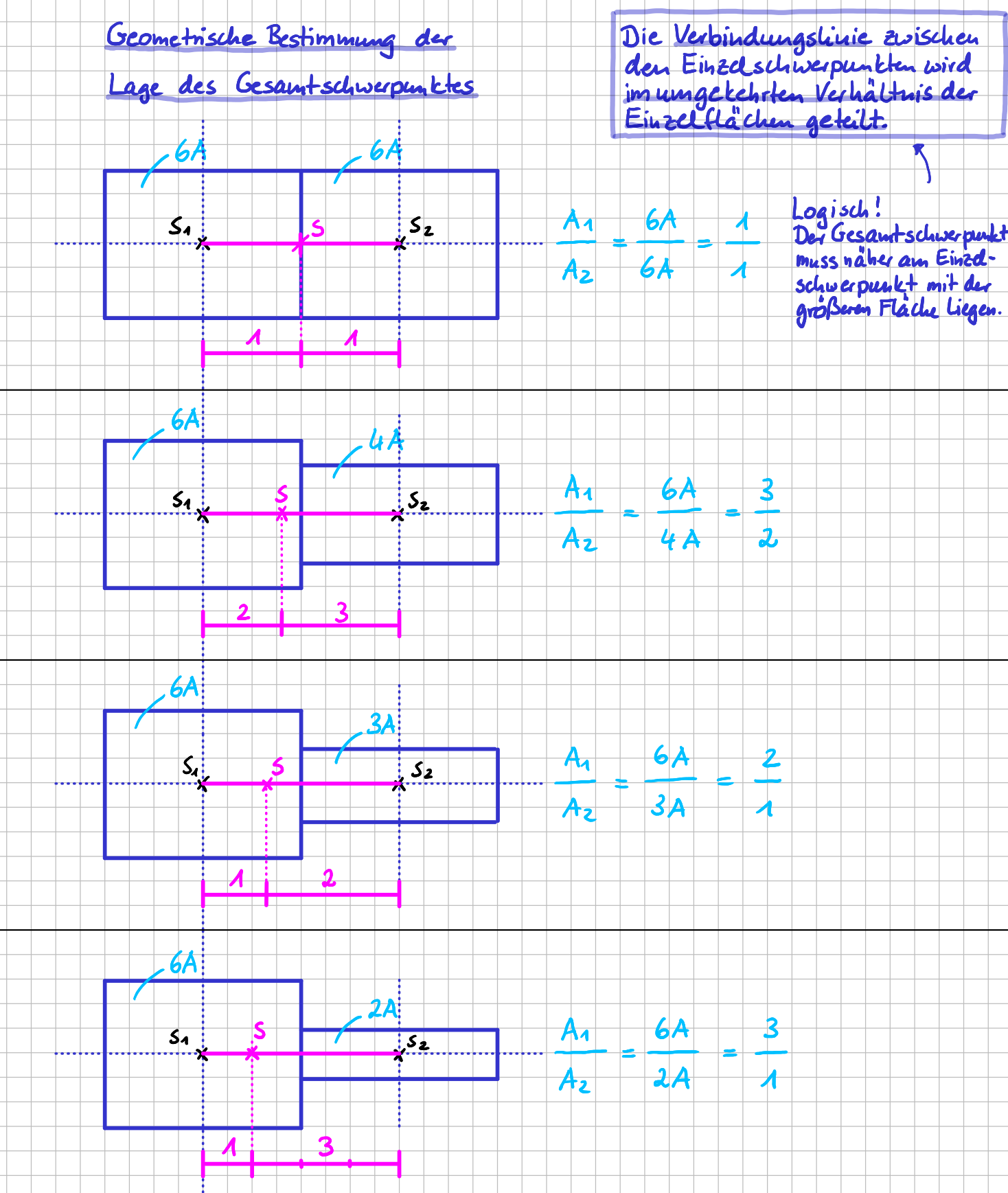
Beispiele für unterschiedliche Flächenverhältnisse: im umgekehrten Verhältnis wird die Verbindungslinie der Einzelschwerpunkte durch den Gesamtschwerpunkt geteilt
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Beispiele_fuer_unterschiedliche_Flachenverhaeltnisse.png
Die Regel mit dem Teilen der Verbindungsstrecke gilt natürlich auch, wenn die Verbindungslinie nicht horizontal angeordnet ist. Dann lässt sich das Teilungsverhältnis auch auch die horizontale und vertikale Richtung übertragen, wie es in folgendem Beispiel zu sehen ist. Mathematisch gesehen sind ähnliche Dreiecke hier eine mögliche Basis für das Verständnis.
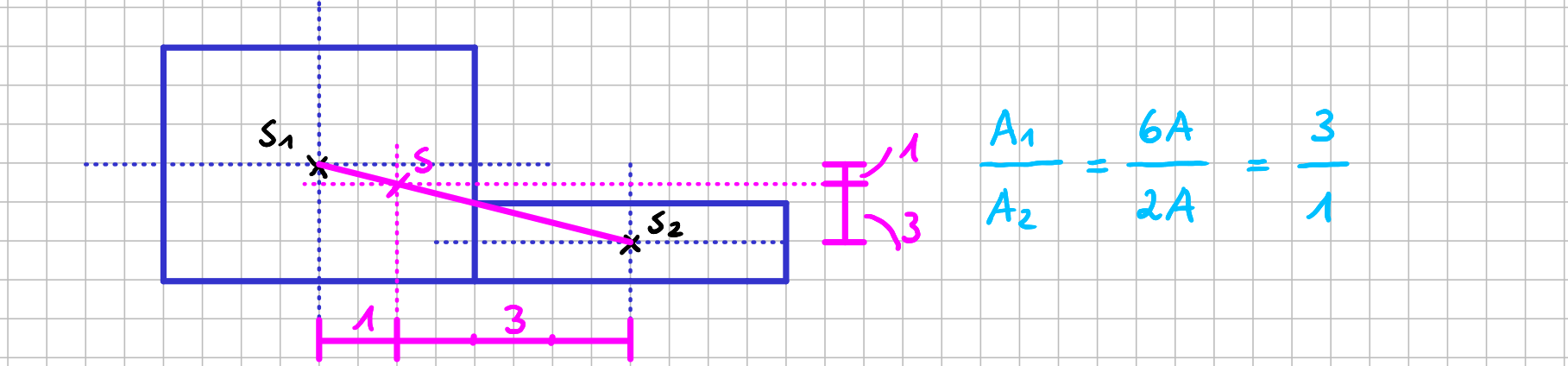
Teilungsverhältnisse bei nicht-horizontaler Lage der Verbindungslinie
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Teilungsverhaeltnisse_bei_nichthorizontaler_Lage.png
Jetzt bleibt noch die Frage, wie wir die bisherigen Erkenntnisse verallgemeinern und systematisch in eine Formel bringen können. Das Ergebnis sieht mit den Schwerpunktskoordinaten \( x_{Si}, y_{Si}, z_{Si} \) der Teilflächen \( A_i \) so aus:
Formeln für die Berechnung der Koordinaten des Gesamtschwerpunktes
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Formeln_fuer_die_Berechnung_der_Lage_des_Gesamtschwerpunktes.png
Wie gut, dass die mathematische Schreibweise so kurz und klar ist. Ansonsten müssten wir die Formel für die \( x \)-Koordinate des Gesamtschwerpunktes so schreiben ...
Formel für die Berechnung der x-Koordinate des Gesamtschwerpunktes in Worten
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Formle_fuer_die_x_Koordinate_in_Worten.png
... was auch hilfreich ist, da nochmal in einer anderen Darstellung klar wird, was da physikalisch gesehen eigentlich überhalb und unterhalb des Bruchstrichs steht.
Im folgenden Video zeige ich dir am konkreten Beispiel eines Lastenrads, das mit drei Kartons und einem Teppich beladen ist, wie du eine Schwerpunktskoordinate mit der Summenformel berechnen kannst.
Mit Essen soll man ja nicht spielen. Aber beim Essen ein kleines Experiment auszuführen ist nach meiner Auffassung erlaubt. Mit einer Scheibe Toastbrot, die z.B. auf einem Brett balanciert wird, kannst du sehr gut überprüfen, wie sich die Schwerpunktslage verändert, wenn noch ein Element hinzukommt (ein Stück Käse) oder ein Element weggenommen wir (einmal beherzt abbeißen). Auf dem ersten Foto siehts du den Versuchsaufbau. Auf dem zweiten Bild ist in rot markiert, wo das Brett langläuft, wenn nur das Toastbrot ausbalanciert wird. Jetzt habe ich rechts ein Stück Käse auf das Toastbrot gelegt und das Brett so verschoben, dass das Toastbrot mit Käse im Gleichgewicht ist. Die blaue Linie kennzeichnet jetzt die Position des Bretts. Auf dem dritten Bild siehst du anhand dieser blauen Linie, dass sich der Gesamtschwerpunkt für den Fall "Toastbrot mit Käse" nach rechts verschiebt, da ich den Käse an die rechte Kante der Toastscheibe gelegt habe. Der Gesamtschwerpunkt verschiebt sich auch nach rechts, wenn ich links durch Abbeißen Masse wegnehme. Das siehts du anhand der Linien im vierten Bild.
Frühstücksversuch zur Schwerpunktsbestimmung
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Fruehstuecksversuch_zur_Schwerpunktsbestimmung.png
Lass uns den Toastbrotversuch auch gleich mal rechnerisch nachvollziehen. Wie dir sicherlich aufgefallen ist, haben wir bisher noch gar kein Koordinatensystem, verwendet, sondern rein geometrisch argumentiert. Und wie immer gilt: Der Physik ist es egal, wie wir unser Koordinatensystem wählen. Wir können also nichts falsch machen, uns allerdings bemühen, die Lage des Koordinatensystems möglichst clever zu wählen. Und da ich bei dem Versuch darauf geachtet habe, dass alle Veränderungen symmetrisch sind, können wir eine Koordinatenachse auch auf die Symmetrieachse legen. Damit wissen wir schon mal sicher, dass die \( y \)-Koordinate des Gesamtschwerpunktes Null ist, also \( y_S=0 \) gilt. Die \( x_S \)-Koordinate können wir mit der besagten Formel leicht ausrechnen.
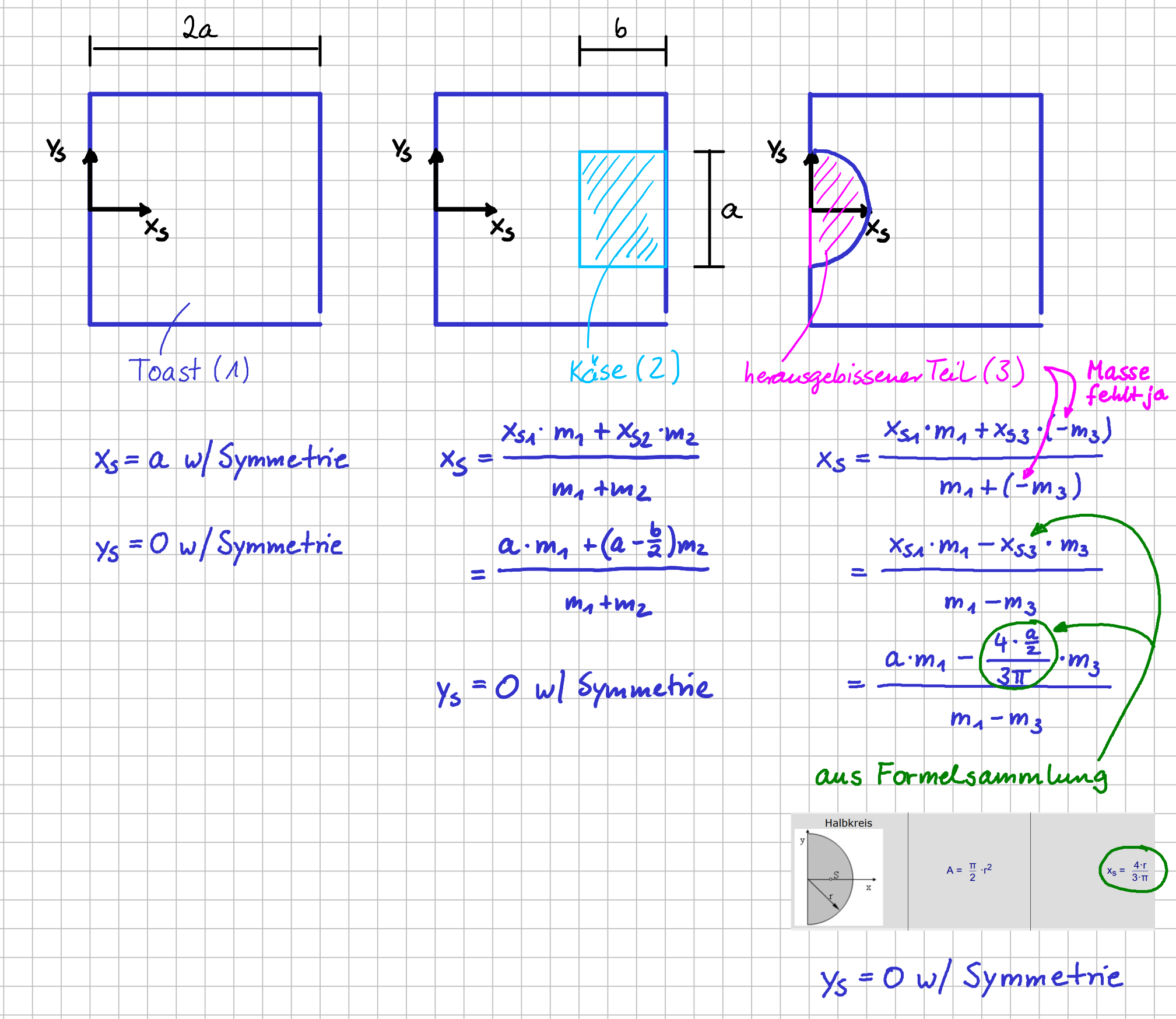
Frühstücksversuch in Formeln
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Fruehstuecksversuch_in_Formeln.png
Im folgenden Video erkläre ich dir nochmal an einem anderen Beispiel, nämlich einer Arbeitsplatte, aus der ein Loch für die Spüle ausgesägt wurde, wie du Ausschnitte oder Löcher bei der Berechnung von Schwerpunkten berücksichtigen musst.
Du kannst dir sicherlich vorstellen, dass es schnell unübersichtlich wird, wenn du mehr als zwei Massen oder Flächen zu berücksichtigen hast und du die Werte gleich in die der Bruchschreibweise mit Summen in Zähler und Nenner reinschreibst. Um die Übersicht zu behalten, ist es hilfreich, alle benötigten Werte und deren Produkte erstmal in einer Tabelle zusammenzustellen, dann über die Spalten zu summieren und nur die Ergebnisse aus den Spalten in den jeweiligen Bruch zu schreiben. Wie das geht, siehst du im Beispiel in der folgenden Abbildung. Ich habe bewusst verschiedene Rechenwege gewählt, damit du siehst, dass es sich lohnt, dir vorab Gedanken zu machen und alles Wissen, wie z.B. das über Symmetrien aber auch über mögliche Zerlegungen der Gesamtfläche zu nutzen.
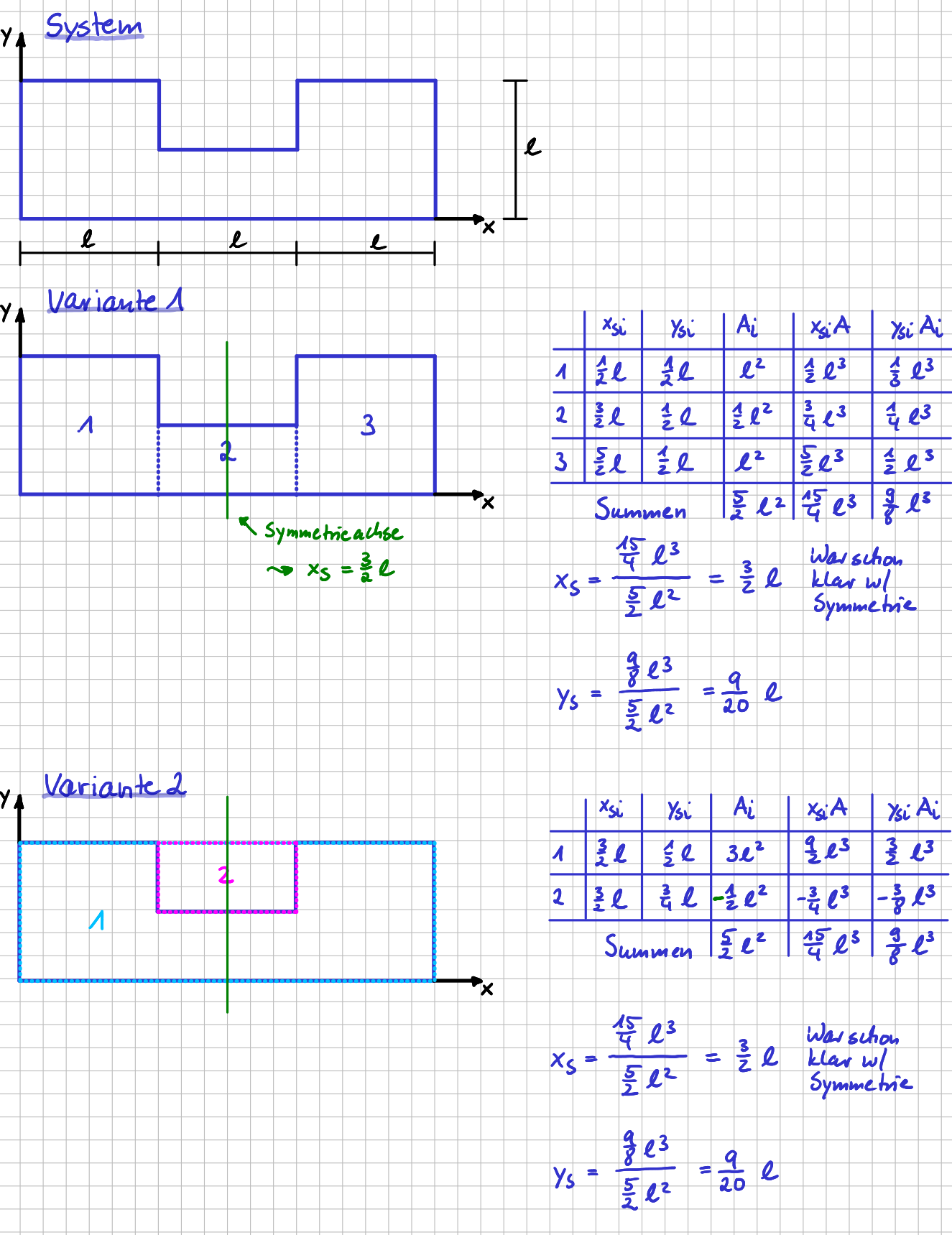
Übersicht behalten mit tabellarischer Erfassung der Werte
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Uebersicht_behalten_mit_Tabelle.png
Zusammenfassung Schwerpunkt bei einfachen Geometrien
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2203/Zusammenfassung_Schwerpunkt_einfache_Geometrien.png
Tipp: Es ist hilfreich eine Formelsammlung zu haben, aus der du für viele Standardgeometrien die Schwerpunktslagen ablesen kannst. Von der Firma Schaeffler gibt es das "Technische Taschenbuch", in dem du im Kapitel "Mathematik eine umfangreiche Sammlung genau solcher Daten findest. Du kannst dir das "Technische Taschenbuch" im Netz runterladen.
Arbeitsblatt - Teste dein Wissen
Schwerpunkt zum Schmunzeln7. Körper mit nicht so einfacher Geometrie
Körper mit nicht so einfacher Geometrie
Coming Soon
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://writemd.rz.tuhh.de/uploads/a887ef45-e8fc-4f7d-8356-d5e71e1543e6.png
Im folgenden Video findest du mit Beispiel 3 direkt ein Anwendungsfeld aus der Mechanik selbst. Wenn du eine Streckenlast, die von einer Funktion begrenzt wird, zu einer resultierenden Einzelkraft zusammenfassen willst, musst du ja auch die Lage der Wirkungslinie dieser Einzelkraft bestimmen. Da die Wirkungslinie der Einzelkraft durch den Schwerpunkt der von der Streckenlast überspannten Fläche geht, kannst du also direkt die Formel für die Bestimmung der Schwerpunktskoordinate in x-Richtung anwenden.
Zusammenfassung - Das Wichtigste in Kürze
Zusammenfassung Schwerpunkt bei nicht so einfachen Geometrien
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13823/mod_book/chapter/2204/Zusammenfassung_Schwerpunkt_nicht_so_einfache_Geometrien.png