Actio = Reactio

Für das, was Isaac Newton in seinem dritten Axiom formuliert hat, gibt es verschiedene Bezeichnungen. Manche sprechen von Gegenwirkungsprinzip, manche von Wechelswirkungsprinzip und manche von Actio = Reactio. Die letzte Formulierung verwendet lateinische Begriffe, also Begriffe aus der Sprache, in der Newton Ende des 17. Jahrhunderts seine Erkenntnisse aufgeschrieben hat.

Was besagt denn nun dieses Prinzip?

Kräfte treten immer paarweise auf: Wenn ein Körper 1 auf einen anderen Körper 2 eine Kraft (actio) ausübt , so wirkt eine gleich große, aber entgegen gerichtete Kraft (reactio) von Körper 2 auf Körper 1. Beide Kräfte liegen auf derselben Wirkungslinie.

Dasselbe gilt übrigens auch für Momente: Wenn ein Körper 1 auf einen anderen Körper 2 ein Moment (actio) ausübt, so wirkt ein gleich großes, aber entgegen gerichtetes Moment (reactio) von Körper 2 auf Körper 1.
Beide Momente liegen auf derselben Wirkungslinie.

Schauen wir uns "Actio = Reactio" gleich mal an zwei Beispielen beim Freischneiden von Lagern an.

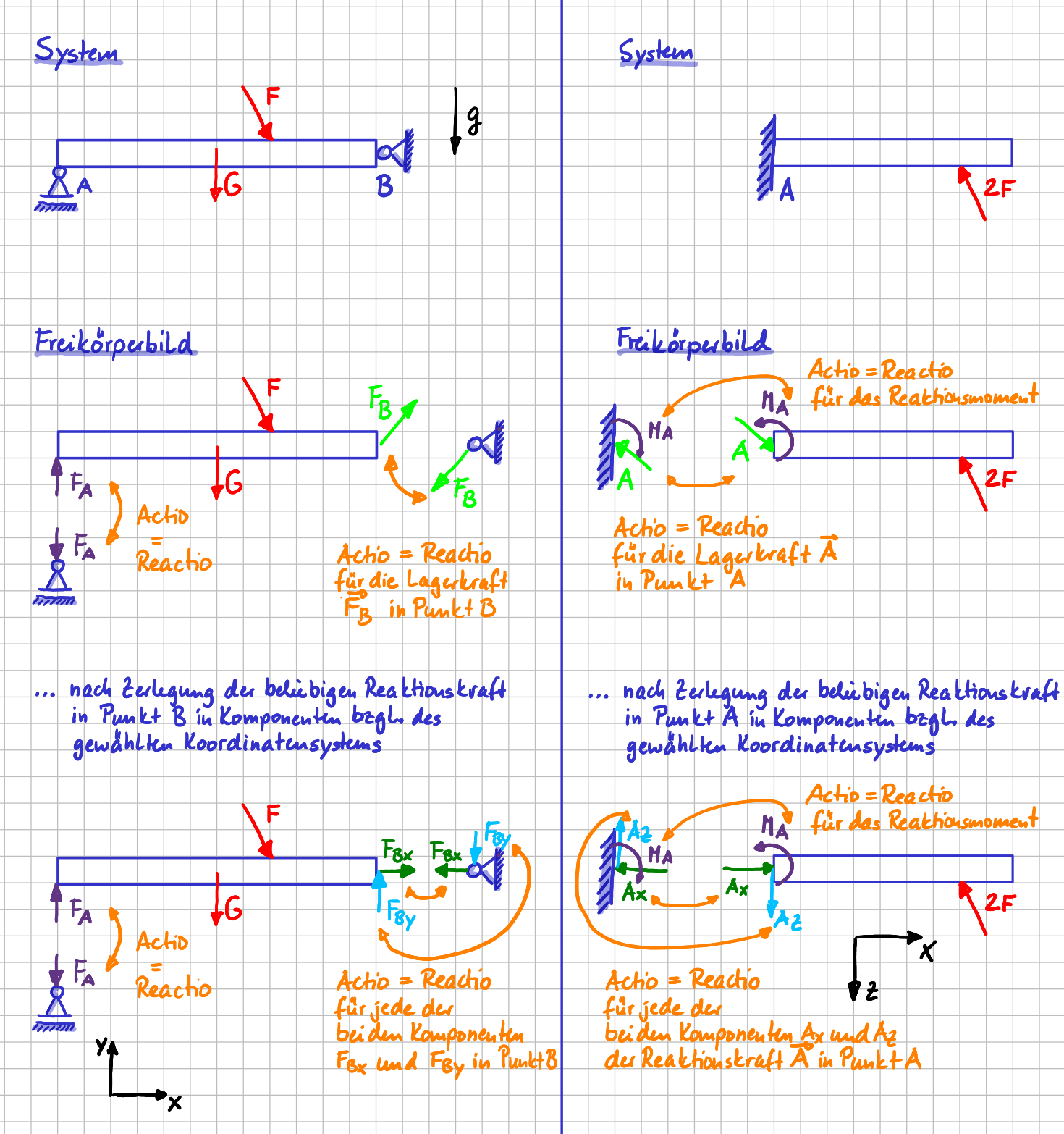
Actio = Reactio für zwei Systeme mit unterschiedlichen Lagern

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13821/mod_book/chapter/2196/Actio_gleich_Reactio_fuer_zwei_Systeme_mit_unterschiedlichen_Lagern.png

Im linken System tritt im Loslager im Punkt A eine Reaktionskraft auf, deren Richtung bereits bekannt aber deren Betrag unbekannt ist. Im Punkt B, dem Festlager, kann eine -nach Betrag UND Richtung- beliebige Reaktionskraft übertragen werden. Sowohl für die Lagerkraft in A als auch in B gilt, dass sie zwei Mal auftreten: jeweils einmal am Balken und einmal am Lager; sie haben dieselbe Wirkungslinie und die entgegengesetzte Richtung.
Auch für die Komponenten der Lagerkraft in B, die sich bei der Zerlegung bezüglich der Achsen des gewählten Koordinatensystem ergeben, gilt natürlich Actio = Reactio.

Im rechten System kann in der festen Einspannung ein beliebige Reaktionskraft und ein Moment übertragen werden. Die Argumentation für die Reaktionskraft ist identisch der Argumentation beim Festlager. Aber auch für das Reaktionsmoment gilt: Das Reaktionsmoment tritt doppelt auf, einmal am Balken, einmal an der Wand. Die Richtung der beiden Momente ist entgegengesetzt und die Wirkungslinie ist identisch.

Jetzt wirst du vielleicht denken: "Ok, also mit den Reaktionsgrößen, also Reaktionskräften und -momenten, passt das mit dem Actio = Reactio.  Was aber ist mit der Kraft F und der Gewichtskraft G im linken Beispiel von eben? Die sind doch nur einmal vorhanden ?!?"

Schauen wir doch nochmal genauer auf das Beispiel 1 von eben.

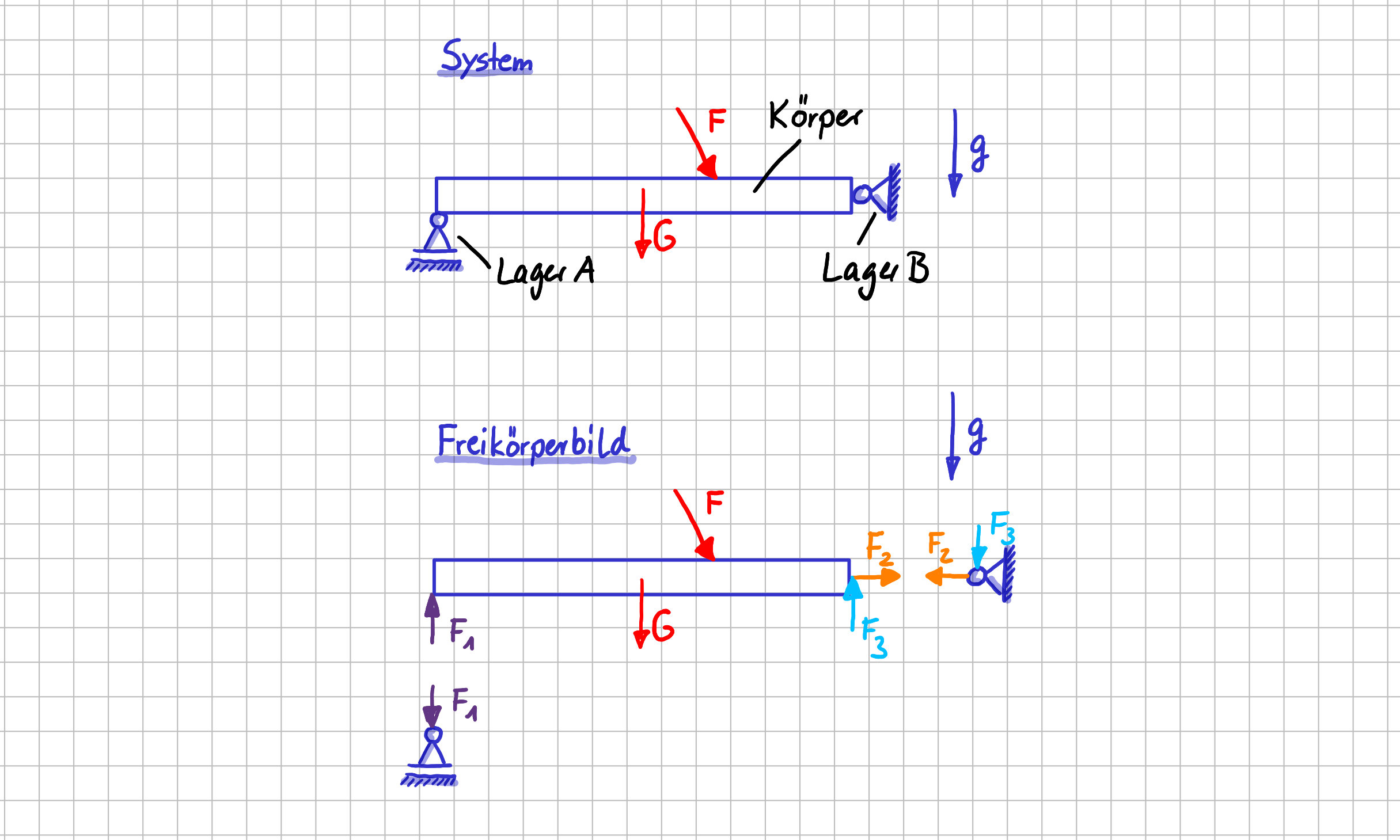
Actio = Reactio unter der Lupe - Ansicht 1

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13821/mod_book/chapter/2196/Actio_gleich_Reactio_unter_der_Lupe_01.png

Genau an der Stelle lohnt es sich, stufenweise ein Stück weiter rauszuzoomen.

Machen wir den ersten Zoomschritt. dafür reichen ein bis zwei Schritte rückwärts. Dann sieht das Bild so aus:

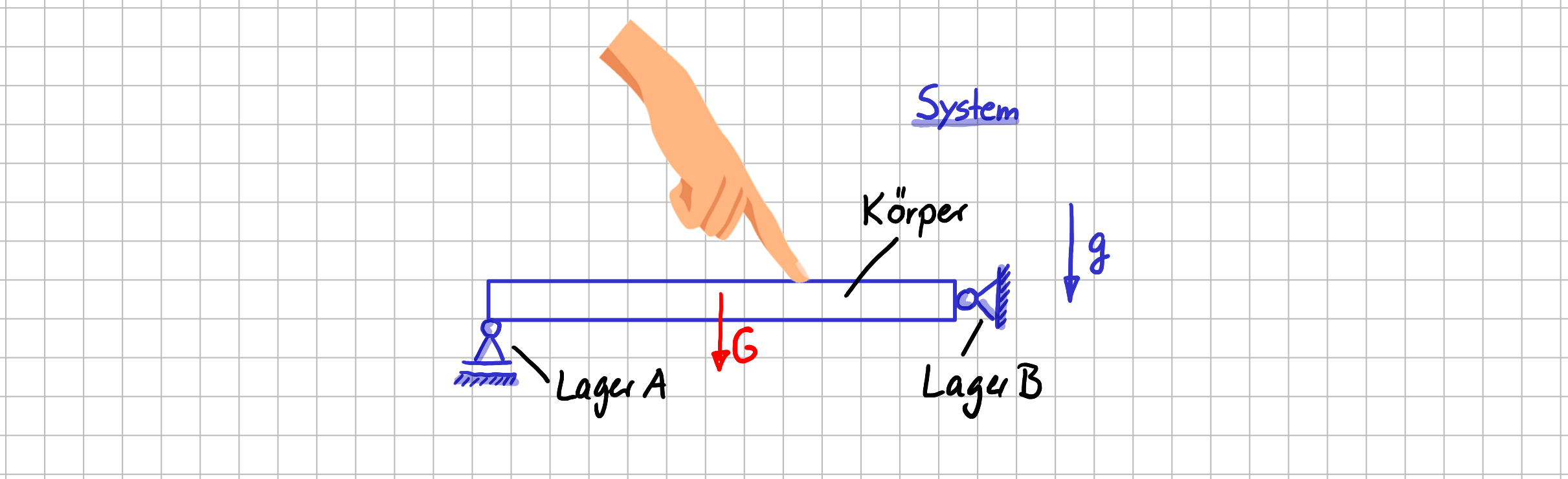
Actio = Reactio unter der Lupe - Ansicht 2

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13821/mod_book/chapter/2196/Actio_gleich_Reactio_unter_der_Lupe_02.png

Aha! Die Kraft \(\vec{F} \) kommt gar nicht aus dem Nichts, sondern daher, dass jemand mit dem Finger auf den Körper drückt. Das bedeutet also, dass wir unser Freikörperbild erweitern können.

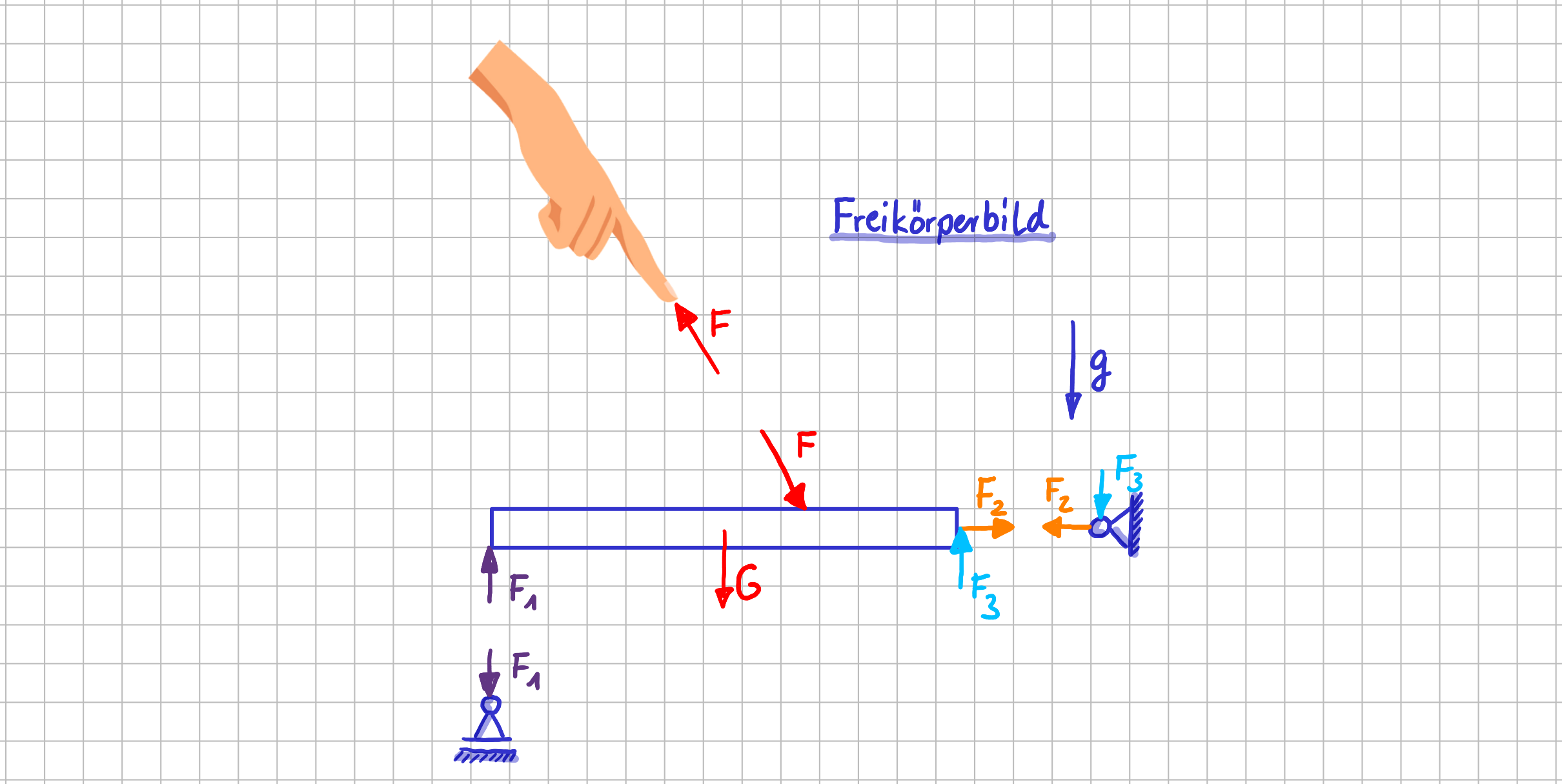
Actio = Reactio unter der Lupe - Ansicht 3

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13821/mod_book/chapter/2196/Actio_gleich_Reactio_unter_der_Lupe_03.png

Und dann ist die Kraft \(\vec{F} \) auf einmal auch doppelt vorhanden: in dem Maße, in dem der Finger auf den Körper drückt, drückt der Körper auf den Finger zurück: Actio = Reactio. Die beiden Kräfte liegen auf einer Wirkungslinie, sind entgegengesetzt von der Richtung her und haben den gleichen Betrag. Das passt jetzt also auch schon mal mit dem Gegenwirkungsprinzip.

Und was ist jetzt noch mit der Gewichtskraft \(\vec{G} \)? Dazu müssen wir noch einen weiteren Zoomschritt machen ... und zwar dieses Mal einen großen ... einen ganz großen ... raus in den Weltraum.
Wenn wir jetzt also von außen auf die Erde schauen, dann können wir mit einer Speziallupe sehen, dass da gerade jemand auf der Erdoberfläche unser Experiment durchführt und mit einem Finger auf einen Balken drückt.

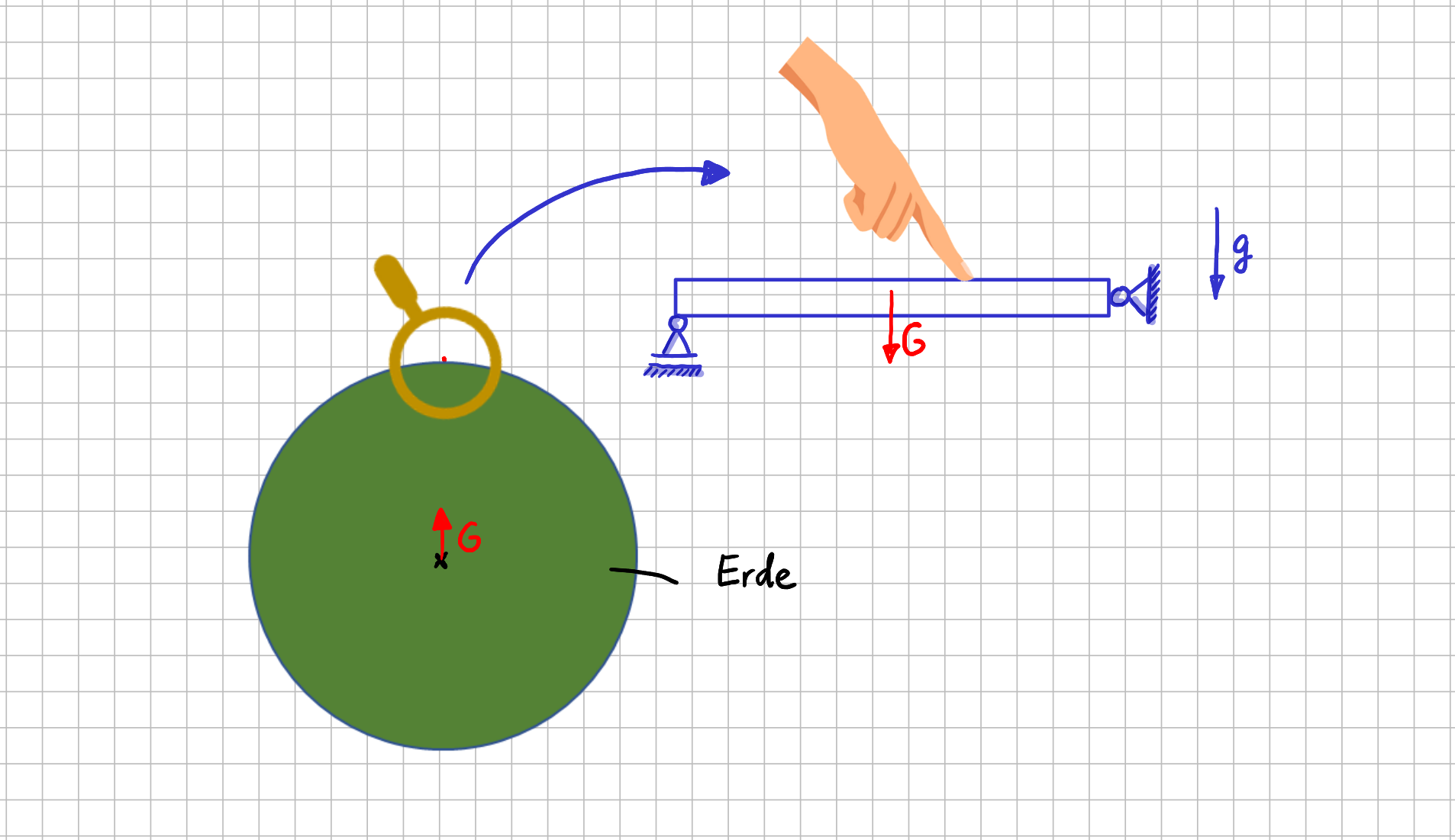
Actio = Reactio unter der Lupe - Ansicht 4

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13821/mod_book/chapter/2196/Actio_gleich_Reactio_unter_der_Lupe_04.png

Und jetzt wird auch klar, dass es auch für die Gewichtskraft \(\vec{G} \) eine Gegenkraft gibt, die das Paar komplett macht. Sie greift im Erdmittelpunkt an.
Die Gewichtskraft beruht ja darauf, dass es zwischen zwei beliebigen Objekten nach dem Gravitationsgesetz eine Anziehungskraft gibt. Zwischen Erde und Körpern auf der Erdoberfläche ist diese Anziehungskraft von merklicher Größe. Und da die Anziehungskraft als Einzelkraft im Schwerpunkt eines jeden Objektes berücksichtigt werden kann, greift sie auf der Seite der Erde (näherungsweise) im Erdmittelpunkt an.
Problem gelöst: Auch für die Gewichtskraft gilt Actio = Reactio und die Aussage des Gegenwirkungsprinzips passt auch hier.
Schon beeindruckend, was Isaac Newton, und er war ja nicht der einzige Wissenschaftler, der sich damals mit solchen Fragestellungen beschäftigt hat, letztendlich zusammengetragen und aufgeschrieben hat, oder?

Arbeitsblatt - Teste dein Wissen

Freischneiden und Actio= Reactio rauf und runter - Teil 1

Freischneiden und Actio= Reactio rauf und runter - Teil 2