Trigonometrie: Satz des Pythagoras

4. Rechtwinkliges Dreieck

4.1. Satz des Pythagoras

Satz des Pythagoras

Für rechtwinklige Dreiecke gibt es einen ganz besonderen Zusammenhang zwischen den Längen der Seiten. Dieser Zusammenhang ist unter dem Namen Satz des Pythagoras bekannt.
Hier findest Du drei verschiedene Formulierungen für diesen Satz:

Variante 1:
Der Flächeninhalt des Quadrates über der einen Kathete plus der Flächeninhalt des Quadrates über der anderen Kathete ist gleich dem Flächeninhalt des Quadrates über der Hypothenuse.

Variante 2:
Die Länge der einen Kathete ins Quadrat plus der Länge der anderen Kathete ins Quadrat ist gleich der Länge der Hypothenuse ins Quadrat.

Variante 3:
Wenn mit $ c $ die Hypothenuse des rechtwinkligen Dreiecks bezeichnet ist $ a $ und $ b $ die beiden Katheten sind, gilt $$a^2+b^2=c^2$$

Welche Variante ist für dich am einfachsten zu merken? Damit meine ich: Mit welcher Variante verstehst du am besten, was die Aussage des Satzes des Pythagoras ist?
Im folgenden Bild ist Variante 1 graphisch veranschaulicht.

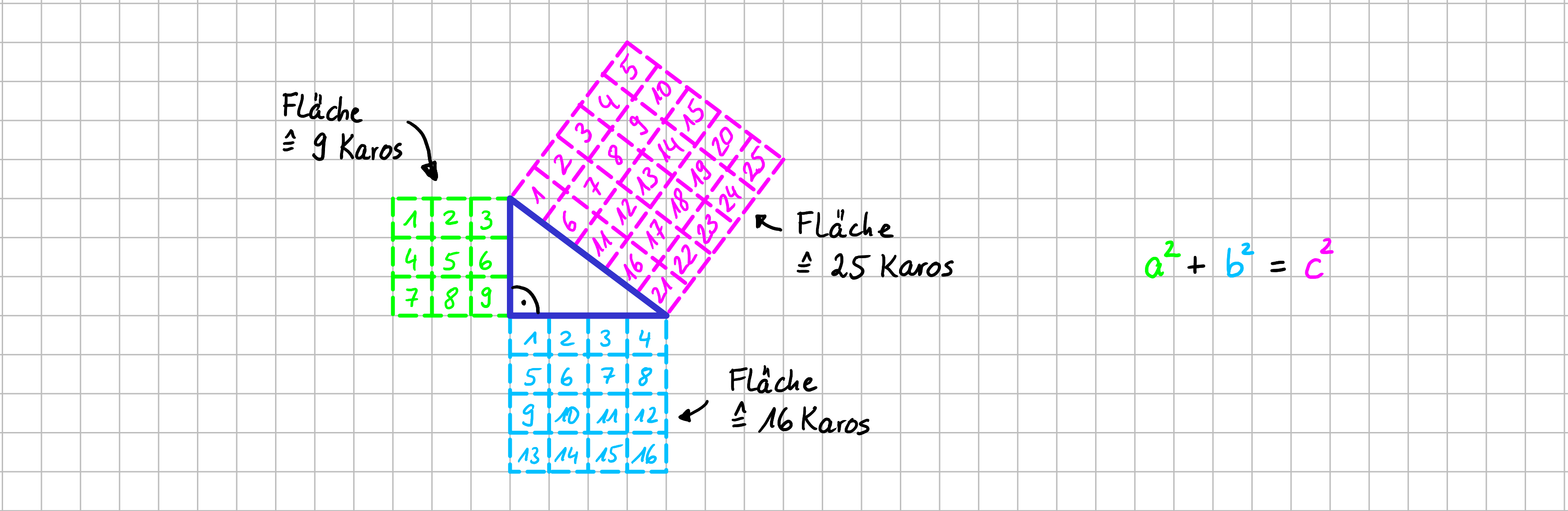
Satz des Pythagoras ausführlich

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2134/Satz_des_Pythagoras_ausfuehrlich.png

In vielen Anwendungen kommt der Satz des Pythagoras zum Einsatz, wenn es darum geht, eine Länge bei einem rechtwinkligen Dreieck zu bestimmen. Die Formel muss dann also noch nach der gesuchten Länge aufgelöst werden. Sind z.B. die Längen $ b $ und $ c $ bekannt, gilt für $ a $:
$$a=\sqrt{c^2-b^2}$$