Die Welt beschreiben
| Website: | Hamburg Open Online University |
| Kurs: | Mechanik hautnah |
| Buch: | Die Welt beschreiben |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 3. März 2026, 12:48 |
1. Einstieg
Einstieg "Die Welt beschreiben"
Einer meiner Lieblingsaussagen ist "Der Welt ist es vollkommen egal, ob wir versuchen, sie zu verstehen und zu beschreiben ... und welches Koordinatensystem oder welche Einheit wir dabei wählen. Sie funktioniert so, wie sie funktioniert."
Dennoch sind Koordinatensysteme und Einheiten natürlich total wichtig. Sie sind die Basis dafür, dass wir Berechnungen anstellen und uns vorallem auch mit anderen über Vorgehensweisen und Ergebnisse austauschen können.
Warum machen wir das überhaupt? Naja, aus Sicht der Mechanik z.B. um berechnen zu können, ob eine Brücke hält, um unterschiedliche Reifenmaterialien für Sommer und Winter entwickeln zu können, um Schiffe effizient beladen zu können und vieles mehr.

Konventionen und Regeln machen Sinn.
Weitere Informationen
Es ist allen klar, dass wir in Deutschland auf der rechten Straßenseite fahren. Das wurde als Konvention einmal festgelegt. Und auch, dass es Vorfahrtsregeln gibt, ist sicherlich hilfreich. Solche Konventionen haben viele Vorteile. In allererster Linie sorgen sie für Klarheit ... und im Fall des Straßenverkehrs für weniger Unfälle und mehr Sicherheit.
Auch in der Mechanik hat man sich auf Konventionen geeinigt.
So werden für Koordinatensysteme immer so genannte rechtshändige Koordinantensysteme verwendet. Und als Einheiten werden typischerweise die sogenannten SI-Einheiten verwendet. Für Längen ist das die Einheit Meter. Auch werden bestimmte Größen immer mit bestimmten Buchstaben bezeichnet. Für Winkel werden z.B. kleine griechische Buchstaben verwendet.
Du willst mehr wissen?
Dann lies einfach weiter.
2. Koordinatensystem
Koordinatensystem
Wir bewegen uns im dreidimensionalen Raum. Typischerweise verwenden wir daher Koordinatensysteme mit drei zueinander senkrecht stehenden Achsen. Irgendjemand hat mal festgelegt, dass diese Achsen im deutschprachigen Raum mit \(x\), \(y\) und \(z\) bezeichnet werden. Im amerikanischen Sprachraum sind z.B. die Buchstaben \(i\), \(j\) und \(k\) üblich.
Nachdem die Bezeichnung der Achsen festgelegt war, musste noch die Reihenfolge festgelegt werden. Man hat sich darauf geeinigt, die drei Koordinatenachsen in einem sogenannten Rechtssystem oder rechtshändigen System anzuordnen.
Du ahnst es schon: Du kannst die Richtung der drei Koordinatenachsen zueinander bestimmen, indem Du deine rechte Hand verwendest.
Strecke Daumen und Zeigefinger so aus, dass sie im rechten Winkel zueinander stehen. Jetzt spreizt du den Mittelfinger noch so ab, dass er senkrecht auf der Ebene steht, die durch Daumen und Zeigefinger gebildet wird.
Wenn du jetzt die Finger noch so den Koordinantenachsen zuordnest
Daumen : \(x-\)Achse
Zeigefinger: \(y-\)Achse
Mittelfinger: \(z-\)Achse
dann kannst du überprüfen, ob ein gegebenes Koordinatensystem ein rechtshändiges Koordinatensystem ist. Oder du kannst rausfinden, in welche Richtung die dritte Koordinatenachse zeigt, wenn nur zwei gegeben sind.
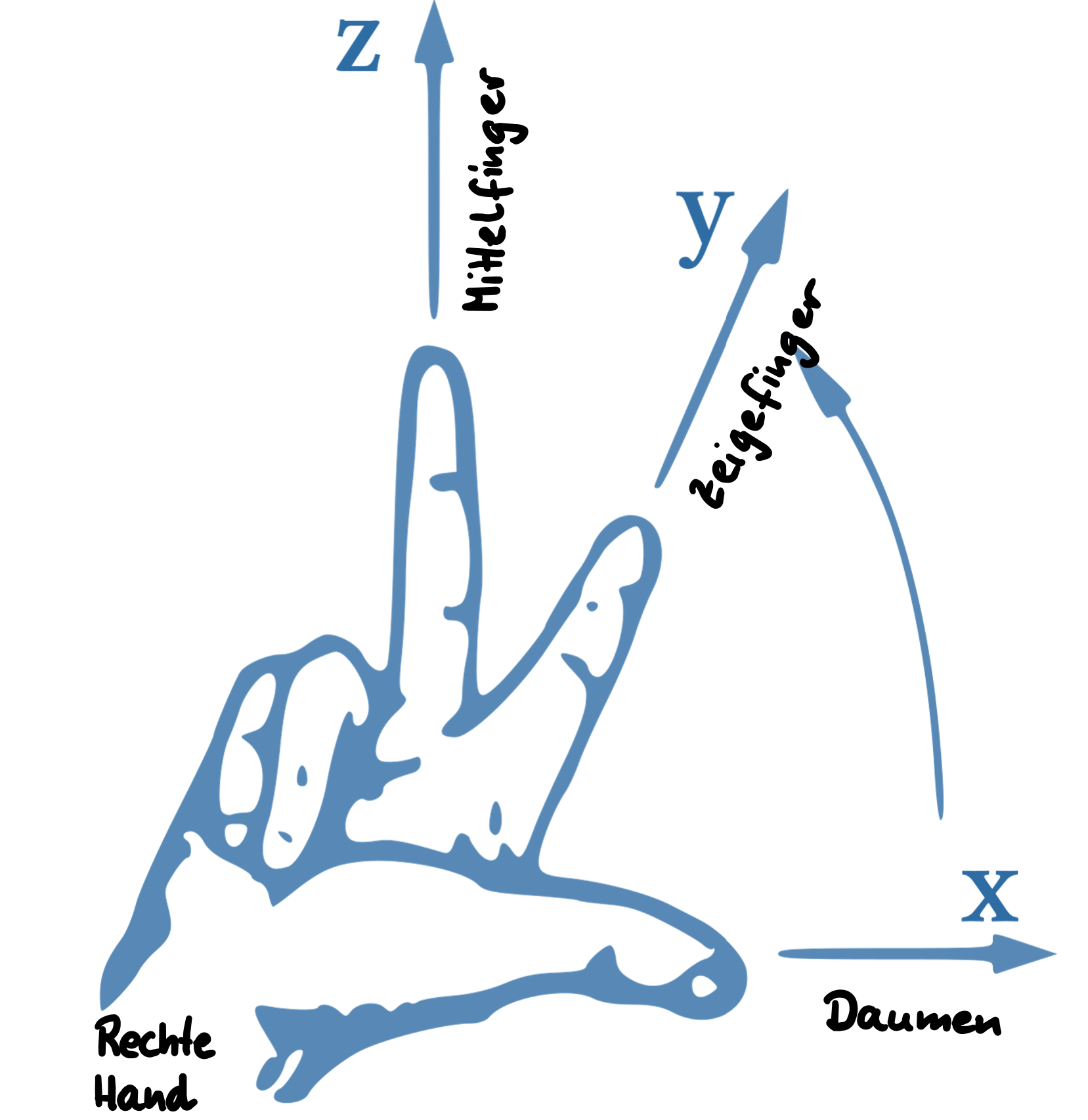
Rechte-Hand-Regel für Koordinatensysteme
Weitere Informationen
Wikipedia, Ausschnitt mit Ergänzungen
https://de.wikipedia.org/wiki/Rechtssystem_%28Mathematik%29#/media/Datei:Koordinatensysteme_L+R.svg
Tests
3. Einheiten und typische Bezeichnungen
Einheiten
Das Internationale Eineitensystem oder SI (Système international d’unités) ist ein System für physikalische Größen, das weltweit verbreitet ist.
Alle SI-Einheiten sind über sieben physikalische Größen definiert
| Basisgröße | Einheit | Zeichen für Einheit |
|---|---|---|
| Zeit | Sekunde | \(\mathrm{s}\) |
| Länge | Meter | \(\mathrm{m}\) |
| Masse | Kilogramm | \(\mathrm{kg}\) |
| Elektrische Stromstärke | Ampere | \(\mathrm{A}\) |
| Thermodynamische Temperatur | Kelvin | \(\mathrm{K}\) |
| Stoffmenge | Mol | \(\mathrm{mol}\) |
| Lichtstärke | Candela | \(\mathrm{cd}\) |
In der Statik haben wir nur mit den ersten drei Basisgrößen zu tun, genauer gesagt in vielen Fällen mit sogenannten abgeleiteten Größen wie z.B. einer Kraft, einem Moment oder einer Fläche.
Schauen wir doch einfach mal die Einheiten und Bezeichnungen typischer physikalischer Größen in der Mechanik an:
| physikalische Größe | typisches Formelzeichen | Einheit mit SI-Einheiten |
eigener Name | eigene Einheit |
|---|---|---|---|---|
Fläche |
\(A\) | \(\mathrm{m}^2\) | - | - |
Volumen |
\(V\) | \(\mathrm{m}^3\) | - | - |
Masse |
\(m\), \(M\) | \(\mathrm{kg}\) | - | - |
Dichte |
\(\rho =\dfrac{m}{V}\) | \(\dfrac{\mathrm{kg}}{\mathrm{m}^3}\) | - | - |
Erdbeschleunigung |
\(g\) | \(\dfrac{\mathrm{m}}{\mathrm{s}^2}\) | - | - |
Kraft |
\(F\), \(A_x\), \(F_B\), \(Q\) | \(\dfrac{\mathrm{kg} \cdot \mathrm{m}}{{s}^2}\) | Newton | \(\mathrm{N}\) |
Gewichtskraft |
\(G=F_G=m\cdot g\) | \(\dfrac{\mathrm{kg} \cdot \mathrm{m}}{{s}^2}\) | Newton | \(\mathrm{N}\) |
Moment |
\(M\), \(M_y\) | \(\dfrac{\mathrm{kg} \cdot \mathrm{m}^2}{{s}^2}\) | - | \(\mathrm{Nm}\) |
Streckenlast |
\(q\) | \(\dfrac{\dfrac{\mathrm{kg} \cdot \mathrm{m}}{{s}^2}}{\mathrm{m}}\) | - | \(\dfrac{\mathrm{N}}{\mathrm{m}}\) |
Das gute an Einheiten ist, dass du sie immer auch nehmen kannst, um zu überprüfen, ob du richtig gerechnet hast. Du kannst also einen sogenannten Einheitencheck durchführen.
Wenn du also ein Volumen ausrechnen sollst und etwas herausbekommst, das die Einheit \(m^2\) hat, ist also klar, dass du dich verrechnet hast ... was ja nicht weiter schlimm ist. In diesem Fall kannst du dich also auf die Suche machen und gucken, wo der Meter verlorengegangen ist.
Vielleicht hast du dir angewöhnt, ein Endergebnis immer doppelt zu unterschreiben, damit du die Übersicht behälst. Gewöhn dir am besten gleich noch an, in diesem Zuge die Einheiten deines Ergebnisses zu überprüfen. Das geht mit etwas Übung total schnell.
