Vektorrechnung
2. Was ist ein Vektor eigentlich?
2.2. Betrag
Betrag eines Vektors
Der Betrag wird auch die Länge eines Vektors genannt und wird mit \(a=\left|\vec{a}\right|\) bezeichnet. Der Betrag eines Vektors \(a\) lässt sich über verschiedene "Denkweisen" bestimmen.
Denkweise 1: geometrische Betrachtung = Satz des Pythagoras
Aus einer geometrischen Betrachtung heraus ergibt sich der Betrag \(a\) über den Satz des Pythagoras direkt zu
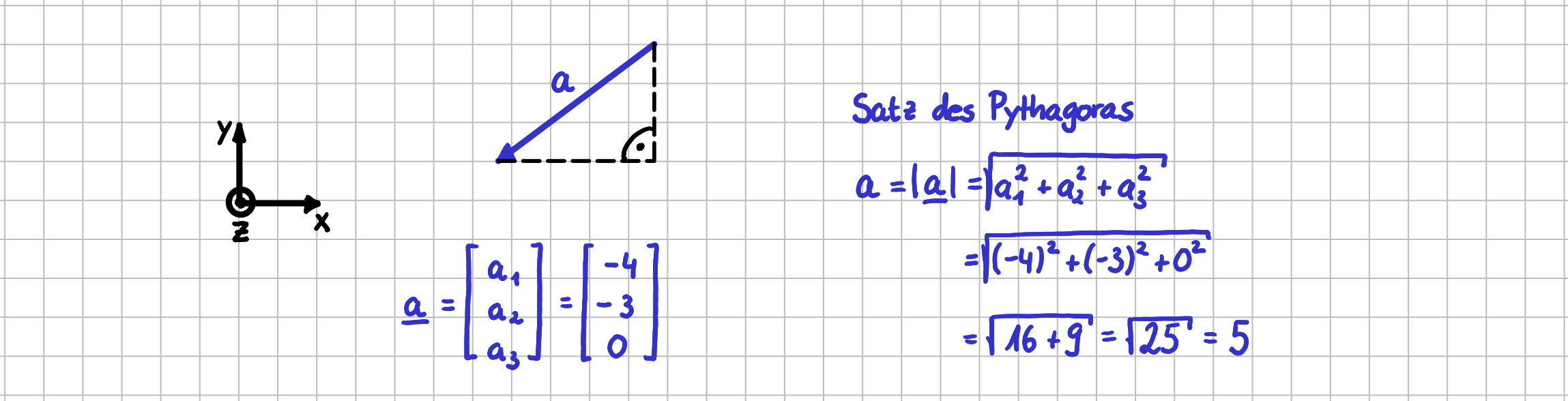
Vektorlänge und Pythagoras
Weitere Informationen
Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0
https://learn.hoou.de/pluginfile.php/13788/mod_book/chapter/2144/Verktorlaenge_und_Pythagoras.png
Wird ein Vektor skalar mit sich selber malgenommen, ist der eingeschlossene Winkel 0°, so dass mit \(\cos(0°)=1\) gilt $$\vec{a} \cdot \vec{a} = a \cdot a \cdot \cos(0°)=a^2$$
$$\vec{r}=\begin{pmatrix} 3b \\ 4b \\ 5b \end{pmatrix}$$
$$\mathrm{Pythagoras} \quad \left|\vec{r}\right|=r=\sqrt{(3b)^2+(4b)^2+(5b)^2}=\sqrt{9b^2+16b^2+25b^2}=\sqrt{2 \cdot 25b^2}=5\sqrt{2}b$$
$$\mathrm{Skalarprodukt} \quad \left|\vec{r}\right|=r=\sqrt{\begin{pmatrix} 3b \\ 4b \\ 5 b \end{pmatrix} \cdot \begin{pmatrix} 3b \\ 4b \\5 b \end{pmatrix}}=\sqrt{9b^2+16b^2+25b^2}=\sqrt{2 \cdot 25b^2}=5\sqrt{2}b$$
Zusammenfassung - Das Wichtigste in Kürze
Betrag eines Vektors
Der Betrag eines Vektors gibt die Länge des Vektors an. Er kann mittels des des Satzes von Pythagoras oder mittels des Skalarproduktes berechnet werden:
 Berechne den Betrag eines Vektors
Berechne den Betrag eines Vektors