Trigonometrie

Allgemeines Dreieck

Im allgemeinen Dreieck gibt es – bis auf die Winkelsumme – keinerlei Vorgaben für die Winkel.

Damit es übersichtlich bleibt, sind hier noch einmal die bereits eingeführten Bezeichnungen dargestellt. Sie gelten für alle folgenden Unterabschnitte.

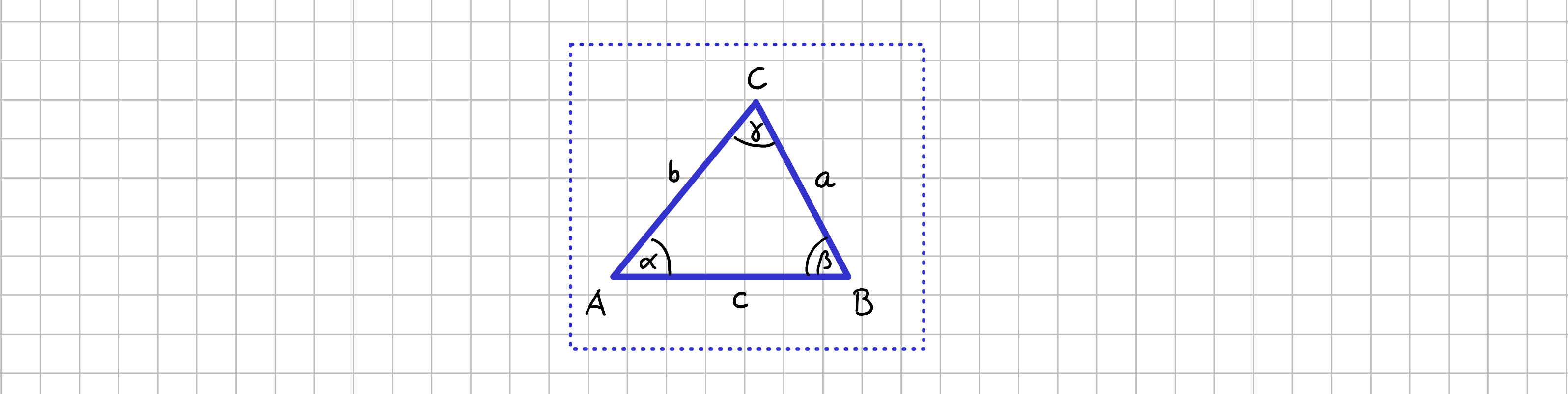
Standardbezeichnungen beim Dreieck

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2137/Standardbezeichnungen_beim_Dreieck.png

Die Winkelsumme

Die Summe aller Winkel in einem Dreieck beträgt immer 180°:
$$\alpha + \beta + \gamma =180°$$

Der Sinussatz

Das Verhältnis aus dem Sinus eines Winkels und der Länge der dem Winkel gegenüberliegenden Seite ist konstant:
$$\frac{\sin\alpha}{a} = \frac{\sin\beta}{b} = \frac{\sin\gamma}{c}$$

Der Cosinussatz

Auch für das allgemeine Dreieck gibt es einen Zusammenhang zwischen den Quadraten der dre Seitenlängen. Er lautet:
$$c^2=a^2+b^2-2ab\cos\gamma$$

Für den Fall, dass  \( \gamma = 90° \)  gilt, ist  \( \cos(90°) = 0 \)  und der hintere Term verschwindet. Wenn es sich um ein rechtwinkliges Dreieck handelt, wird der Cosinussatz also zum Satz des Pythagoras.

Zusammenfassung - Das Wichtigste in Kürze

• Winkelsumme: \( \alpha + \beta + \gamma =180° \)
  


• Sinussatz: \( \dfrac{\sin\alpha}{a} = \dfrac{\sin\beta}{b} = \dfrac{\sin\gamma}{c} \)
  


• Cosinussatz: \( c^2=a^2+b^2-2ab\cos\gamma \)
  

Standardbezeichnungen beim Dreieck

Weitere Informationen

Johanna Peters - Mechanik hautnah | TU Hamburg
CC BY 4.0-Lizenz
https://learn.hoou.de/pluginfile.php/13787/mod_book/chapter/2137/Standardbezeichnungen_beim_Dreieck.png